盾构机主驱动密封结构优化研究*

谭 锋 杨 博 黄 乐 丁剑平 李正波

(1.广州机械科学研究院有限公司 广东广州 510535；2.华南理工大学材料科学与工程学院 广东广州 510641)

盾构机是一种用于铁路[1]、公路[2]、水利[3]、煤矿[4]及城市轨道交通[5]等地下隧道空间快速开挖的现代化综合性技术装备，具有施工方便、挖掘速度快以及安全系数高等优点。盾构机由许多复杂的系统组成，其运用到机、电、液、传感、信息等技术，涉及到机械、土木、地质、力学、控制、材料等多门学科。因此，盾构机技术的水平代表着一个国家重大技术装备的发展水平。

大型盾构机主驱动密封系统是盾构机的关键系统之一。主驱动系统是刀盘转动的直接动力，可以看做掘进机的“心脏”，而主驱动密封就是其保护膜，因此主驱动密封的性能直接决定机器性能的发挥[6]。相较于国外，我国在此方面的基础理论研究与应用研究起步较晚，所研制的密封系统在施工过程中常因密封异常损坏或严重磨损导致间隙过大而密封失效，进而导致主轴承或齿轮磨损、停工检修，给隧道工程施工带来巨大的安全风险和不可估量的经济损失[7]。而密封系统进口价格高昂，且国外最先进的密封技术对我国封锁，因此为解决密封可靠性差、寿命短等问题，提高国产大型盾构机在国际市场的竞争力，迫切需要开展大型掘进机主驱动密封关键技术研究及应用。

本文作者针对影响盾构机主驱动密封性能的唇形密封圈主要结构参数，建立正交试验方案，并利用有限元分析软件ABAQUS对主驱动密封圈工作过程中的开启压力差及接触宽度进行计算，最后根据主驱动密封工作要求优化出最合适的密封结构。

1 盾构机主驱动密封装配结构

盾构机主驱动密封装配结构如图1所示，图中结构左侧为盾构机外部挖掘面，结构右侧为盾构机主驱动系统内部。

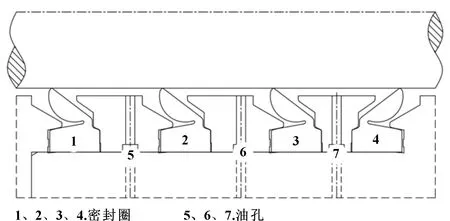
图1 盾构机主驱动密封装配结构

图1中唇形密封圈根据用途可以分为3种：密封圈1起隔离泥水与主驱动内部密封腔的作用，密封圈2、3起降低主驱动密封系统内油压的作用，密封圈4仅起隔离作用。在盾构机工作时，结构左侧外部挖掘面处产生泥水压力，为了防止泥水破坏密封圈进入主驱动系统，在油孔5中打入黏度较大的油脂，同时保持油压大于泥水压力，调节压差使密封圈打开，油脂不断溢出，因此采用密封圈1将泥水与主驱动内部密封腔隔离[8]。由于在油孔5中较大的油压，需要通过密封圈2、3两道密封圈降低主驱动密封系统内油压，因此在油孔6中打入相对油孔5较小的油压，油孔7无需打入油脂。由于油孔7中没有打入油脂，这道腔体作为泄漏检测腔，所以密封圈4仅起隔离作用，以保护主驱动系统内部[9]。

虽然密封圈分为3种，但要求3种唇形密封圈的结构是相同的，因此需要设计一种密封圈同时满足全部要求。考虑到第3种密封圈要求不高，所以只需要满足前2种用途即可。对于第1种用途，要求密封圈可以在较低的压力差下打开；对于第2种用途，需要密封圈能够承受较大的压力差。承压能力具体体现在承压后唇部与轴的接触宽度，接触宽度越小，说明唇形密封圈承压能力越强。

2 有限元模型

2.1 结构模型

唇形密封圈是轴对称结构，在密封圈正常使用的情况下，整个密封圈受力均匀，各个位置变形相同，因此密封圈复杂的三维模型可以简化为二维平面轴对称模型，这种做法可以在不影响计算结果的前提下节省计算所使用的时间，同时大幅提高计算的效率[10-11]，因此，文中研究模型采用了二维平面轴对称模型。

盾构机主驱动密封模型由5个部件组成，因此需建立5个二维轴对称部件，分别为轴、上腔体、下腔体、右腔体以及唇形密封圈部件。将所有部件装配到一起得到整体结构。整体结构的模型如图2所示。

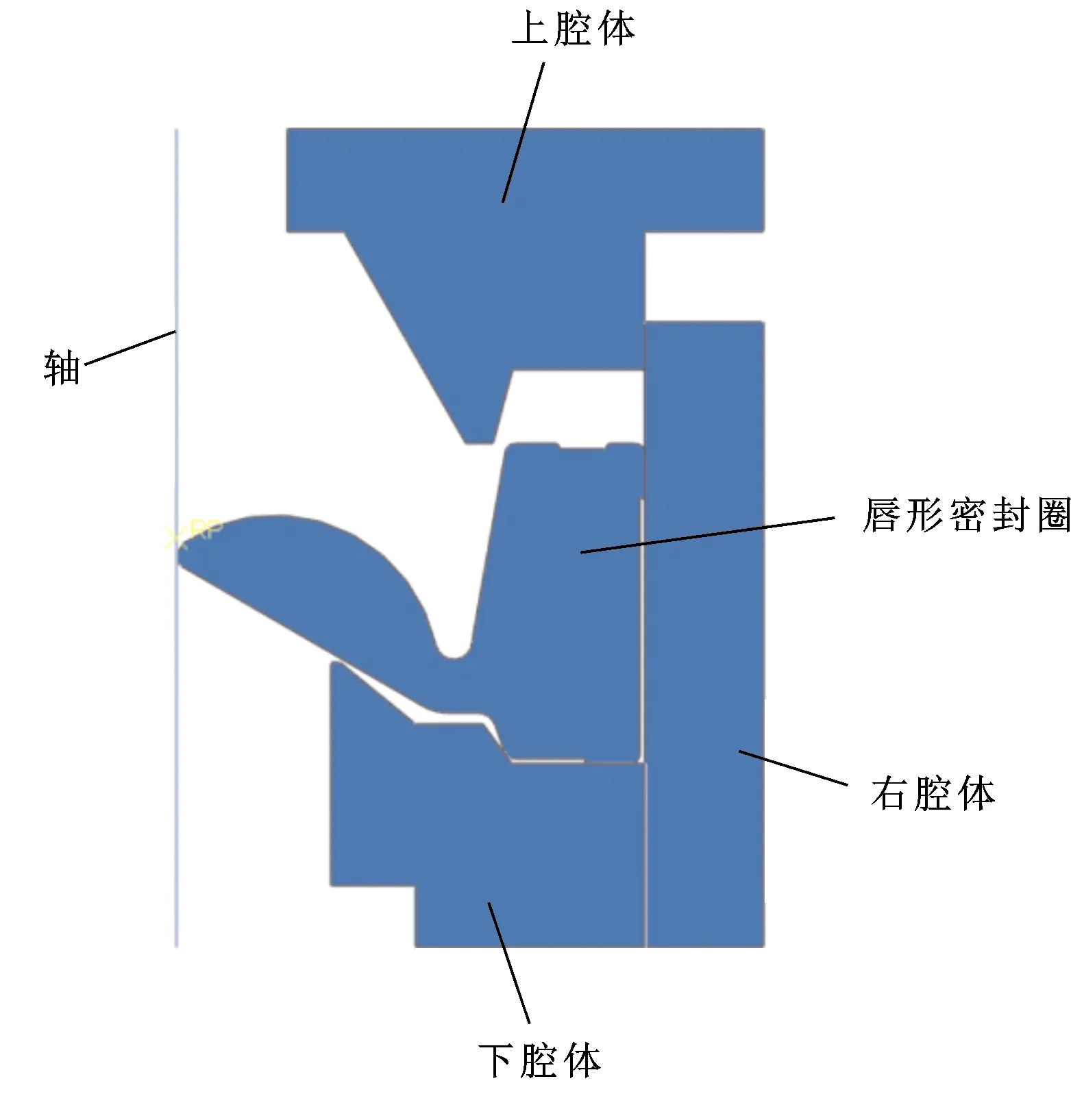
图2 盾构机主驱动密封截面模型

2.2 材料模型

研究的密封圈材料为丁腈橡胶。橡胶材料是一种具有高度非线性的超弹性体，通常被认为具有不可压缩性。在ABAQUS中有多种超弹性的本构模型可以表征橡胶，包括基于热力学统计的Arrude-Boyce模型[12]以及基于唯象学方法的Mooney-Rivlin模型[13]、Yeoh模型[14]、Neo-Hooke模型[15]及Ogden模型等。

通过对丁腈橡胶材料的单轴拉伸、双轴拉伸、平面拉伸以及体积压缩性能的测试，并将测试结果处理并输入到ABAQUS中进行本构模型参数的拟合，得到了不同的本构模型的材料参数。文中试验仿真计算采取常用的Ogden模型，该模型应变能密度表达式由3个主伸长率λ1、λ2、λ3表示，其公式如下：

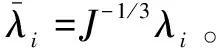
试验采取的Ogden模型阶数N为3[16]，最终拟合得到的材料参数为：μ1=-4.275 444 8，α1=2.124 178 1，μ2=3.580 348 92，α2=3.937 313 78，μ3=2.759 835 51，α3=-1.059 903 9，D1=3.72×10-4，D2=3.12×10-5，D3=-3.18×10-9。其余金属材料采用的弹性模量为200 GPa，泊松比为0.3。

3 结构影响因素分析及正交试验设计

文中主要研究唇形密封圈的结构参数对于密封性能的影响。根据经验，通过对唇形密封圈截面形状的分析，初步选择唇曲度、唇高度、唇宽度和唇厚度作为主要研究的结构参数。优化前的4种参数尺寸如图3所示，其中唇曲度R=18 mm，唇高度为22.35 mm，唇宽度为51.1 mm，唇厚度为5.8 mm。因为所研究的主驱动密封模型中轴的外径、右腔体内径和唇形密封圈的外径是固定的，所以唇宽度的增加会导致装配时压缩值增加，因此唇宽度也可以等效替代为压缩量。

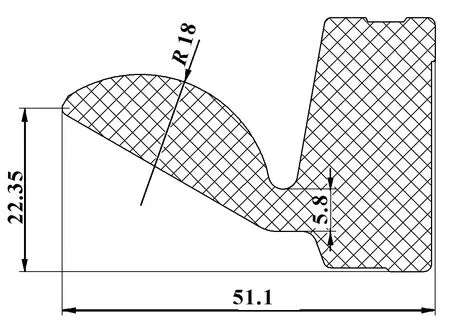
图3 优化前唇形密封圈的主要结构参数(mm)

对唇形密封圈上述4种参数进行正交试验设计，考虑到误差因素加入空白列，选取5因素4水平的正交表。表1为因素水平表，表2为正交试验表。

表1 因素水平

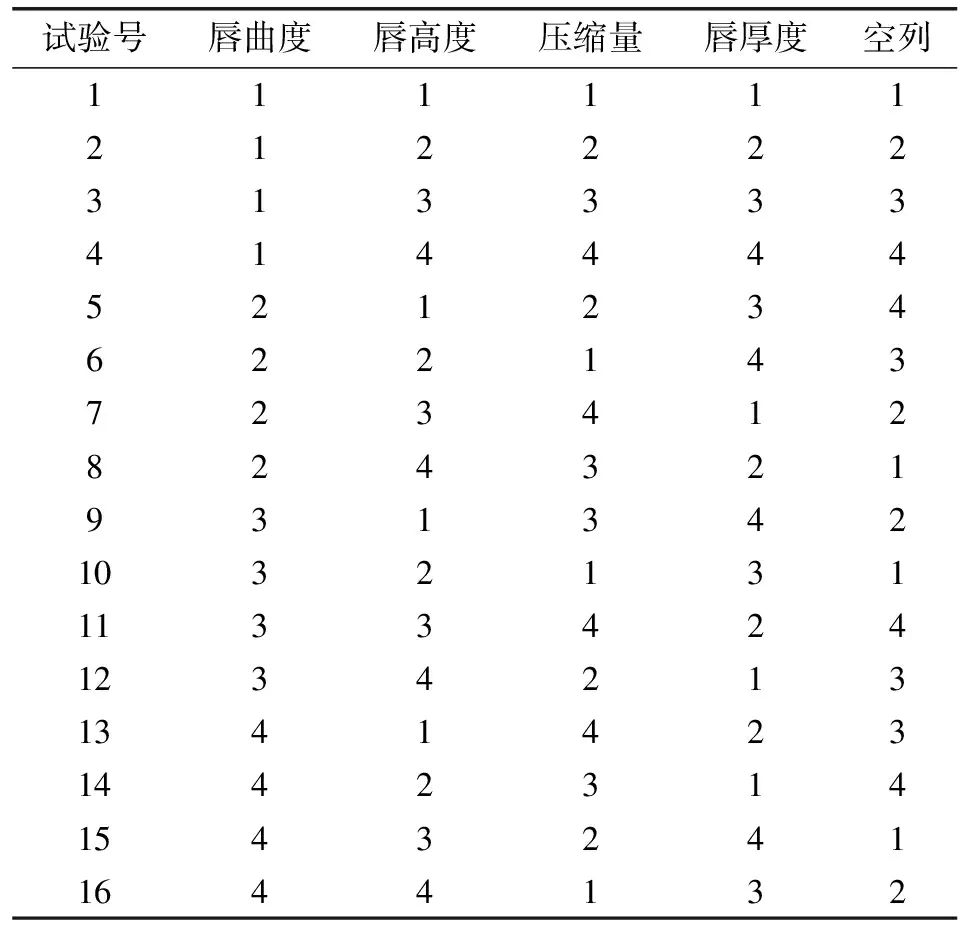
表2 正交试验方案

4 开启压力差的正交分析

通过计算唇形密封圈开启压力差的大小，探究最适用于第一种用途的密封圈结构参数。

4.1 计算方法

计算开启压力差的仿真分析步共分为4步，其中前2个分析步为装配过程，第一步为上腔体向下位移，模拟唇形密封圈的固定过程；第二步为轴向右位移，模拟唇形密封圈的压缩过程。后2个分析步为加压过程，第三步在唇两侧都加1.0 MPa的压力，第四步再把唇下侧压力提升到1.1 MPa，而唇上侧压力不变。

为了使仿真结果更符合唇部实际开启的情况，除了施加压力外，还需要考虑唇与轴接触位置的压力穿透问题，因此需要在唇与轴的接触上施加压力穿透。压力穿透应保持与实际加压的压力一致，因此在第三步中唇与轴接触的两端分别施加压力穿透，接触两端分别定义为起点，临界接触压力和流体压力都设置为1.0 MPa，穿透时间设置为0.001。由于第四步时上侧压力不变，而下侧压力增加为1.1 MPa，因此下侧压力穿透在第四步时临界接触压力和流体压力设置为1.1 MPa，穿透时间设置为0.001。

上述分析步中，第一到第三分析步设置初始增量步为0.01，最大增量步为0.05；第四分析步设置初始增量步为0.001，最大增量步也为0.001。

通过以上载荷的施加，实现了模拟第一种用途时唇形密封圈的受力情况。当在第四分析步时，由于压力及压力穿透施加都是线性施加，即唇下侧的压力随着分析步时长的增加而增加，直至唇打开为止。所以通过唇打开的分析步时长即可得到此时唇下侧的压力大小，进而得到此唇形密封圈结构在泥水压力为1 MPa的开启压力差。例如，唇形密封圈在分析步时长为0.095时仍未开启，而在分析步时长为0.096时开启。这说明在唇下侧压力由1 MPa增加到1.1 MPa的0.096时开启，此时唇下侧压力为1.009 6 MPa，开启压力差为0.009 6 MPa。

4.2 计算结果

通过对唇部开启压力差的计算，得到表3所示结果。

根据各因素不同水平下开启压力的平均值，可以直接得到变化曲线，如图4所示。

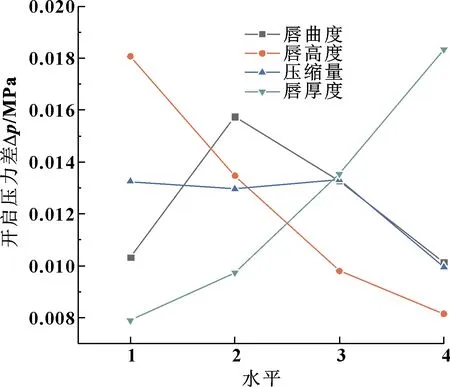
图4 各因素不同水平下唇部开启压力差的平均值

根据极差值R的大小，可以评价几种因素的影响主次。由上述结果可知，影响唇部开启压力差的顺序由大到小依次为唇厚度、唇高度、唇曲度、压缩量。

上述方法只能粗略估计各因素的影响水平，为精确估计各因素的影响大小，需要对结果进行方差分析。

首先需要计算总离差平方和ST，计算方程为

(1)

ST=Q-P

(2)

文中试验ST为0.000 618 55。

其次需要计算各因素的离差平方和Sj，其中误差列的离差平方和Se为误差列离差平方和的和。

(3)

总自由度和任一列自由度的计算公式为

dfT=n-1

(4)

dfj=r-1

(5)

dfe=re-1

(6)

式中：n为进行的试验数总和，n=16；r为此因素的水平数；误差列的自由度dfe为空白列自由度之和。

然后计算每一列的均方，计算方法为

(7)

以上计算结果如表4所示。可以看到所有影响因素的Mj值均大于误差列值Me，因此没有影响因素归于误差列，无需重新计算Me。

接着计算F值，计算公式为

(8)

如果Fj大于F0.01(dfj，dfe)，则此因素对实验结果影响非常显著；如果Fj小于F0.01(dfj，dfe)而又大于F0.05(dfj，dfe)，则此因素对实验结果影响显著；如果Fj小于F0.05(dfj，dfe)，则此因素对实验结果无显著影响。

因此，从表4中可以得到，唇曲度、唇高度和压缩量对实验结果无显著影响，唇厚度对实验结果影响显著。但唇高度的Fj值很接近F0.05(dfj，dfe)，且同时唇高度的极差值与唇厚度的极差值相差不大，因此认为唇高度与唇厚度对实验结果影响显著。误差列的差距小也证明主要影响因素都已经考虑到，无其他显著影响因素。

表4 方差分析计算结果

5 接触宽度的正交分析

通过计算唇形密封圈受压后接触宽度的大小，探究最适用于第二种用途的密封圈结构参数。

5.1 计算方法

计算接触宽度的仿真分析步共分为4步，其中前3个分析步为装配过程，第一步为下腔体向上位移，第二步为上腔体向下位移，这两步模拟唇形密封圈的固定过程；第三步为轴向右位移，模拟唇形密封圈的压缩过程；最后一个分析步为加压过程，在唇上侧加0.5 MPa的压力。

为了使仿真结果更符合唇部实际的情况，和计算开启压力差一样，也需要在唇与轴的接触上施加压力穿透。压力穿透应保持与实际加压的压力一致，因此在第四步中唇与轴接触的上侧施加压力穿透，接触上侧端点定义为起点，临界接触压力和流体压力都设置为0.5 MPa，穿透时间设置为0.001。

上述分析步中，第一到第三分析步设置初始增量步为0.01，最大增量步为0.05；第四分析步设置初始增量步为0.01，最大增量步也为0.01。

通过以上载荷的施加，实现了模拟第二种用途时唇形密封圈的受力情况。计算完毕后，提取计算结果中轴与唇形密封圈的接触宽度即可。

5.2 计算结果

通过对接触宽度的计算，得到表5所示结果。

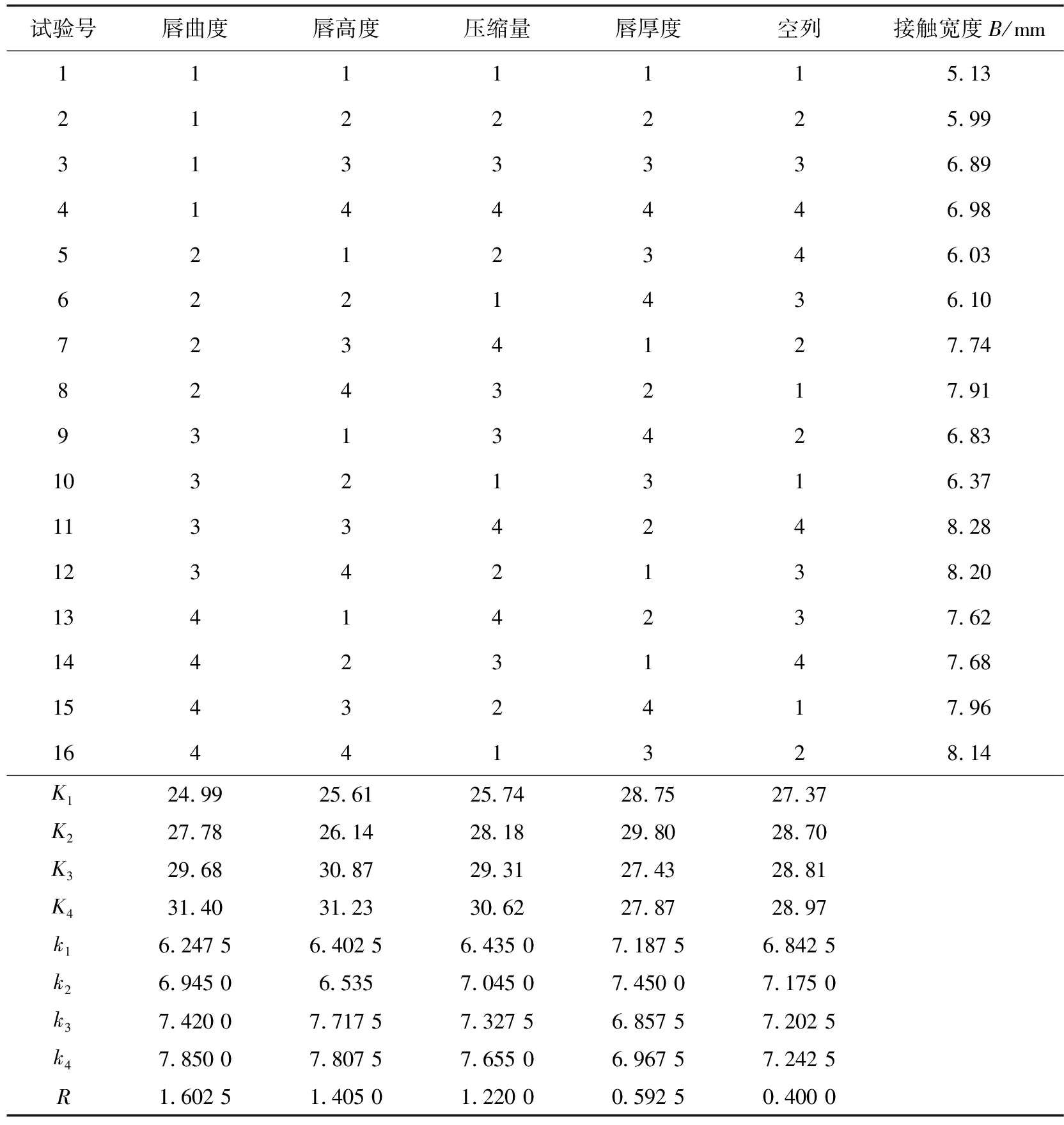
表5 唇部接触宽度的正交试验结果

根据各因素不同水平下接触宽度的平均值，可以直接得到变化曲线，如图5所示。

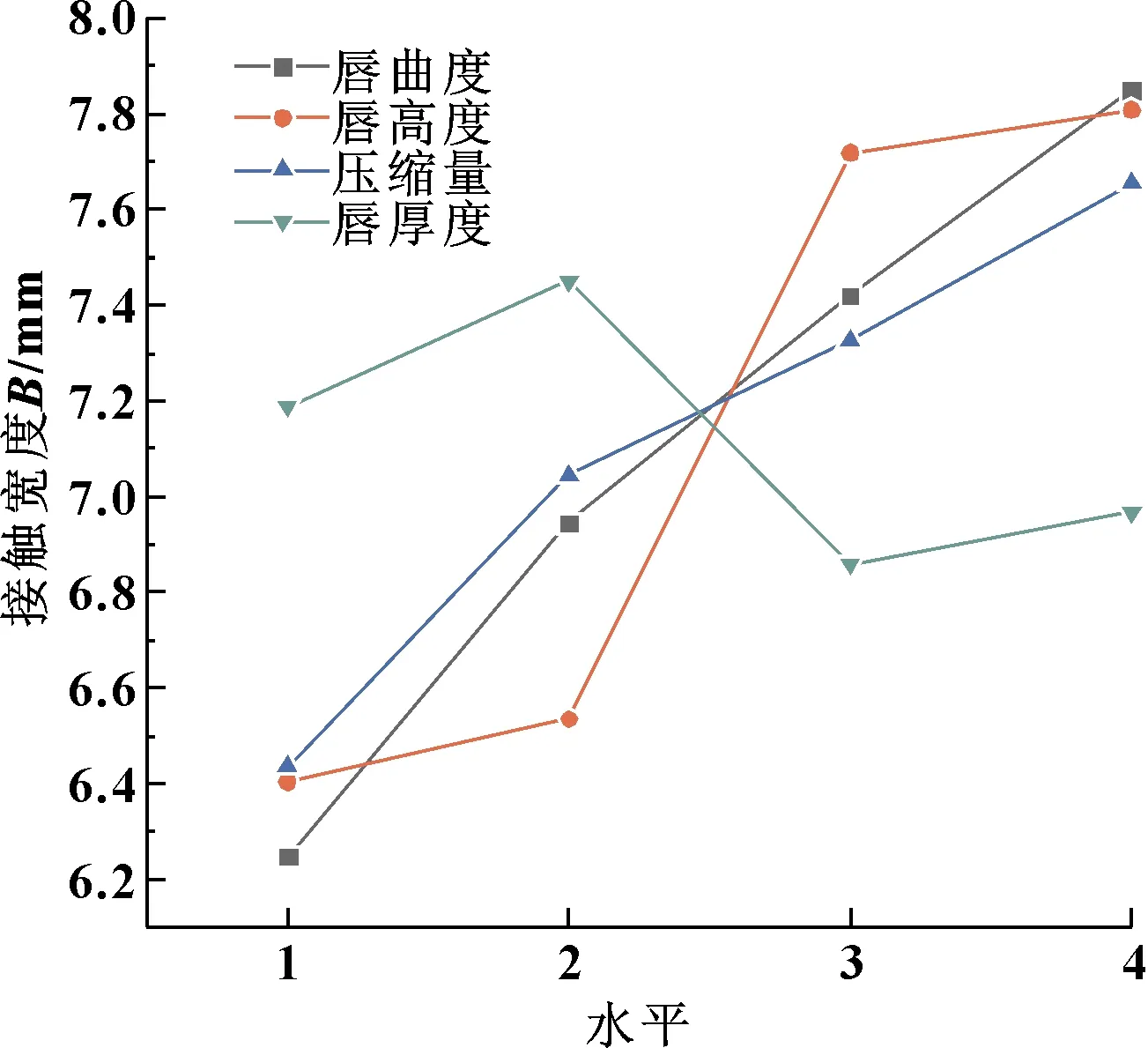
图5 各因素不同水平下唇部接触宽度的平均值

根据极差值R的大小对比，可以评价几种因素的影响主次。由上述结果可知，影响接触宽度的顺序由大到小依次为唇曲度、唇高度、压缩量、唇厚度。

上述方法只能粗略估计各因素的影响水平，为精确估计各因素的影响大小，需要对结果进行方差分析。计算方法同上，结果如表6所示。

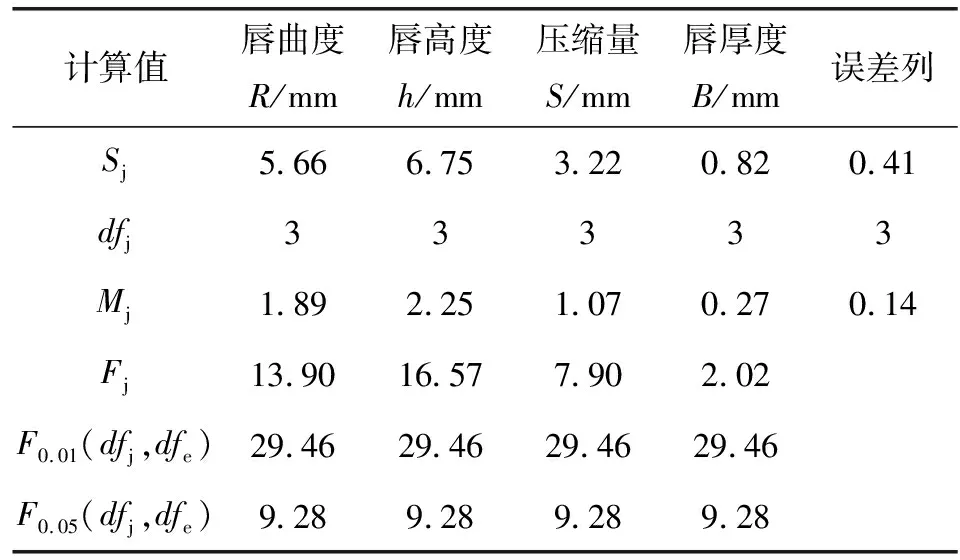
表6 方差分析计算结果

从表6中可以得到，唇曲度和唇高度对实验结果有显著影响，压缩量和唇厚度对实验结果无显著影响，但压缩量对实验结果影响也较大。同时，误差列的差距小也证明主要影响因素都已经考虑到，无其他显著影响因素。

6 主驱动密封结构优化

根据盾构机主驱动密封工作过程的前2种用途，通常希望开启压力差小的同时接触宽度也要小，因此各参数的选择方法如下：

(1)因唇曲度对于开启压力差影响不显著，而对接触宽度影响显著，因此唇曲度参数的选择取决于接触宽度。从图5中可以看到，唇曲度与接触宽度呈现出正相关趋势，所以唇曲度最小时满足接触宽度最小，文中唇曲度选择17 mm。

(2)因唇高度对开启压力差和接触宽度的影响都很显著，而从图4与图5中可以看到，唇高度与开启压力差呈负相关，唇高度与接触宽度呈正相关，唇高度对接触宽度的影响相比对开启压力差更显著，因此应主要根据接触宽度选择参数。文中唇高度选择22.35 mm。

(3)因压缩量对开启压力差和接触宽度影响均不显著，但其对接触宽度影响较大，而从图5中可以看到，压缩量与接触宽度呈正相关，因此应主要根据接触宽度选择参数。文中压缩量选择7.1 mm。

(4)因唇厚度对于接触宽度影响不显著，而对开启压力差影响显著，因此唇厚度参数的选择取决于开启压力差。从图4中可以看到，唇厚度与开启压力差呈现出正相关趋势，所以唇厚度最小时满足开启压力差最小。文中唇厚度选择5 mm。

根据密封圈前2种用途的要求，最终选择唇曲度为17 mm，唇高度为22.35 mm，压缩量为7.1 mm(对应的唇宽度为49.1 mm)，唇厚度为5 mm的唇形密封圈结构。优化后的唇形密封圈结构参数如图6所示。

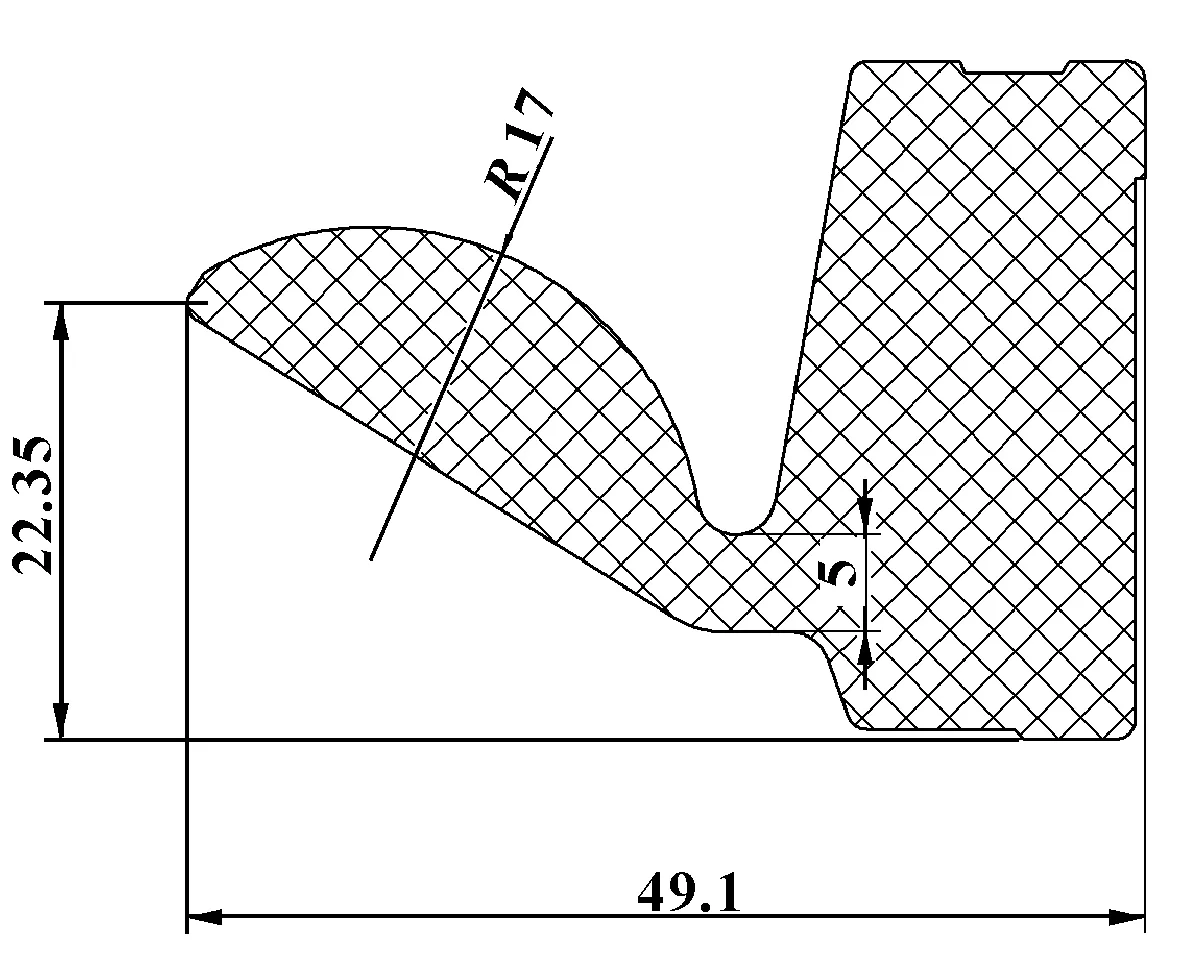
图6 优化后唇形密封圈的主要结构参数(mm)

对结构优化前后的唇形密封圈进行开启压力差及接触宽度的计算，得到结构优化前的开启压力差为0.012 1 MPa，接触宽度为6.97 mm，优化后的开启压力差为0.008 1 MPa，接触宽度为5.36 mm。根据计算可知，优化后开启压力差降低33%，接触宽度降低23%。

7 结论

通过对盾构机主驱动密封主要结构参数的正交试验设计，以及基于有限元分析软件对开启压力差和接触宽度的正交计算与分析，选择最适合盾构机主驱动密封的结构参数。分析结果表明：最适结构的唇曲度为17 mm，唇高度为22.35 mm，压缩量为7.1 mm(对应的唇宽度为49.1 mm)，唇厚度为5 mm。优化后的唇形密封圈与优化前相比开启压力差降低33%，接触宽度降低23%。