基于智能算法的高海拔风电机组多参数优化设计

封焯文，朱世平，赵志华，李子群，宋冬然

（1.中国能源建设集团湖南省电力勘测设计院，湖南长沙 410007；2.中南大学自动化学院，湖南长沙 410083）

0 引言

风力发电发展迅速。截至2019 年，全球风力发电总量已达650 GW，较2001 年的全球风力发电总量24 GW 增加了近27 倍[1]。但是，风电机组运行性能同时受自身约束和外界环境的影响。在高海拔地理条件下，空气密度降低，风电机组发电性能降低，其制造、运输与维护成本显著增加[2]。因此，高海拔机组优化设计对降低风电成本具有现实意义。

目前，对风电机组的成本优化研究主要包含成本建模与优化设计两个方面，而风电机组的成本模型的建立是基础。文献[3]使用了一种经典的风力发电成本模型，但这种成本模型是静态的，不包含运行过程中产生的维修费用和人力成本等，存在一定的缺陷；文献[4]考虑了后期的运维费用，设计了一种动态的成本模型。此外，文献[5]提出了一种成本模型法用于提高风电机组的经济性，并以风轮直径和额定风速为参数进行优化；这种成本模型法并非第一次被提出，早在2006 年文献[6]就对风力发电机的成本模型进行了详细的介绍。此外，文献[7]给出了一种全生命周期成本的概念，涵盖了风电机组从购入到退役整个生命周期的成本，较为全面，建立成本后进一步完成风电机组的优化设计。智能算法作为一种新型的优化方法[8-9]，在电力领域有着许多应用[10-11]，可用于风电机组的优化设计。文献[12]建立成本模型后，利用智能算法对转子直径和额定风速进行优化并在某1 MW 变速风电机组中应用，得到了较好的优化结果。而文献[13]使用平准化电力成本（Levelized Cost of Energy，LCOE）为对象，在对某实际风电场进行蒙特卡罗仿真后，采用遗传算法（Genetic Algorithm，GA）对参数进行优化，得到了优化后的参数。

文献[3-7]所开展的研究仅面向于一般地区的风电机组，而对高海拔风电机组研究不多。文献[14]分析了高海拔地区风电机组与其它地区的区别，文献[15-16]阐述了一般地区与海拔高度之间的联系，而文献[17]以西藏地区为例具体说明了环境因素在高海拔地区的具体变化。文献[18]对高海拔环境下的因素对风力发电的影响进行了分析，文献[19]制定了高海拔风力发电机组的技术规范，而文献[20]设计了一种针对高海拔风电机组设计的改进阴阳对优化算法。尽管如此，相关研究仍较少。因此，本文提出采用智能算法对高海拔风电机组进行优化设计，所取得的研究结果对高海拔风电机组选型与设计具有一定的参考意义。

1 海拔对气候参数及风电机组的影响

高原环境会引起空气密度、大气压力、空气湿度、气温等环境因素的变化，而这些变化会导致风电机组的运行效率低下，甚至损害风机。

1.1 海拔高度对气候参数的影响

高海拔地区有着较为恶劣的自然气候条件，这些气候条件主要由海拔升高引起[13]。海拔升高会导致空气密度、大气压力、日照辐射、温度等一系列的环境变化。表1 显示了空气密度、大气压力等环境参数与海拔高度的关系[14]。海拔升高也会导致雷击概率增大、空气绝对湿度降低、年降水量少、年大风日多、风速变化快、土壤温度低、冻结期长等。高海拔地区的恶劣天气也很多，如雷暴、暴雨、暴雪等。

表1 环境参数与海拔关系Table 1 Relationship between environmental parameters and altitude

1.2 气候环境变化对风电机组的影响

海拔对功率曲线的影响十分明显。功率曲线描述了风电机组输出功率和风速的对应关系，根据贝茨理论，满足贝茨假设的理想风轮从风源处吸收的最大功率Pmax为[21]：

式中：v为转子前方风速；s为风轮扫掠面的面积；ρ为空气密度。

风电机组低压电气部件受到海拔高度的影响为：（1）高海拔会导致电气部件绝缘性能降低。（2）海拔升高会对设备温度产生影响。海拔每升高1 000 m，产品温度会升高约4 K，要求设备额定容量增加。（3）高海拔地区大气压力和空气密度小，设备需降容使用以保证其正常的运行[21]。（4）高海拔地区气压低、空气密度小，应考虑机组绝缘防护和防雷等级，减少雷击带来的不利影响。（5）高海拔地区的太阳辐射会对电力电子系统产生影响。

机械部件受到海拔高度的影响为：（1）对叶片的影响：叶片成本一般占总成本的10%～15%左右[22]，高海拔下叶片运行环境发生很大的变化，导致叶片疲劳度和破损快速达到预警，增加维修成本，降低风电效益[23]。（2）对传动系统的影响：传动系统使用的润滑油在处于低温工况时，油膜的形成以及完好度会受到影响。同时，风机的塔架和机舱等大型部件在温度较低的环境下存在着低温疲劳问题。

2 高海拔风电机组成本模型

建立高海拔风电机组LCOE 模型时，需要将海拔高度考虑到LCOE 模型中。借鉴美国国家可再生能源实验室（National Renewable Energy Laboratory，NREL）提出的技术指标模型[6]，LCOE 模型可为为：

式中：LCOE为平准化电力成本；CAP为年生产成本；EAP为年发电量。

2.1 年生产成本

海拔升高会导致风机的成本增加，在对CAP建模时应考虑海拔高度的影响。CAP表达式为[20]：

式中：CIC为初始资本成本；EAO为年运营成本；RFC为固定费率，是每年每单位初始资本成本中用于支付资本成本、债务和权益回报以及各种其他固定费用的金额。RFC包括建筑融资、融资费用、债务和股本收益、折旧、所得税、财产税和保险等在CIC中所占比例，并且设置为每年0.115 8[6]。

在基于特定假设基础上，建立CIC各部分与海拔高度之间的函数关系，得到改进后的成本列于表2[20]。表2 中，R为转子半径，Pr为额定功率，halt为海拔高度，H为轮毂高度。

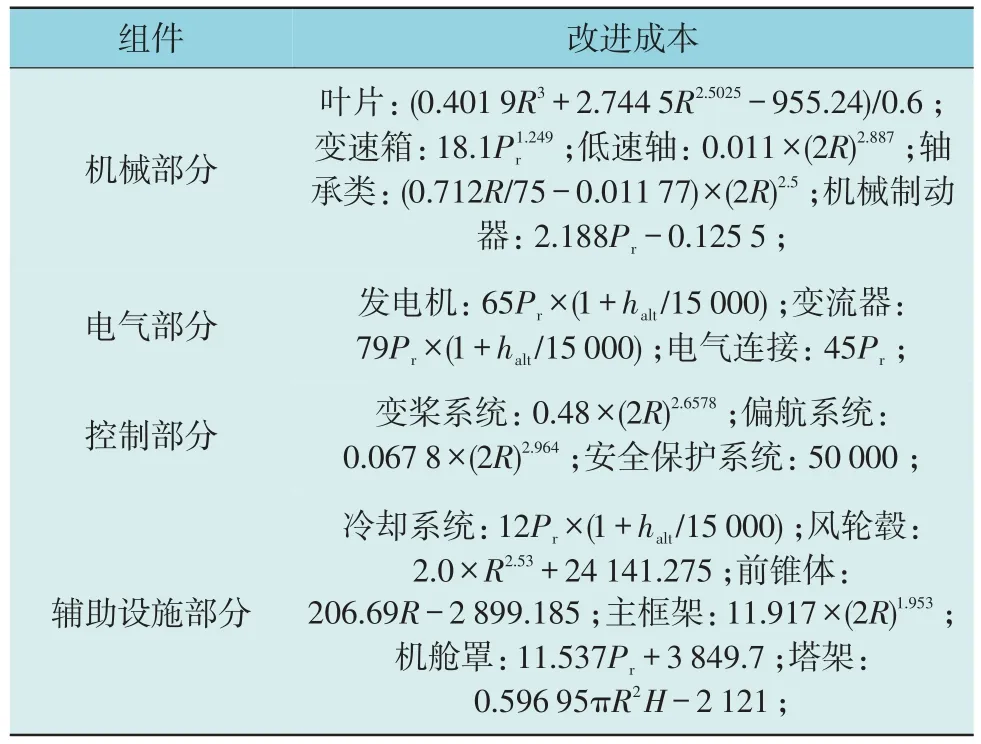
表2 风机各组件改进成本Table 2 Improved cost of wind turbine components ＄

基建成本各部分的改进成本如表3 所示。

表3 基建项目改进成本Table 3 Improvement costs of infrastructure projects ＄

除此之外，还需考虑年运营成本与海拔高度之间的关系。EAO包括土地租赁成本CLL、运行和维护成本COM以及更换/大修成本CLR。在基于NREL给出的原始模型上进行相关优化改进，得到的改进成本如表4 所示。

表4 年运营成本各部分改进成本Table 4 Improved cost of annual operation cost＄

APC 的最终表达式应描述为halt，EAP和3 个风机设计参数R，H，Pr的函数（以gCAP表示）：

2.2 年发电量

风电机组的年度电能输出量EAP为：

式中：Pm为每小时的电能产量；η为电能总损耗，设置为0.17[20]。

从式（5）可以看出，决定年发电量的主要因素Pm为：

式中：P(v)为功率曲线方程；f(v)为风速分布的概率密度，采用主流的Weibull 风速分布模型。两者的表达式分别为：

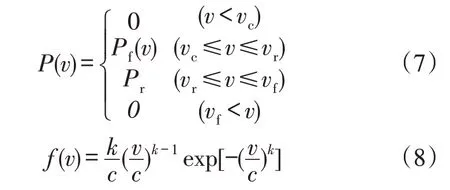
式中：vc为切入风速；vr为额定风速；vf为切出风速；Pf(v)为第Ⅲ区域低于额定风速部分的功率；k为形状参数；c为尺度参数。

根据式（5）-式（8）可以推导出EAP的具体表达式：

2.3 平准化电力成本

根据式（2）-式（9）以及表2-表4 得到考虑海拔高度影响后的LCOE 模型，其具体表达式如下：

在式（10）中，切入和切出风速都是恒定的。当确定风资源参数时，LCOE仅与海拔高度、转子半径、轮毂高度和额定功率有关。因此，在一定的海拔高度下，可以通过选择合适的转子半径、轮毂高度和额定功率来最大程度地降低LCOE。

3 高海拔风电机组成本智能优化

本文采用GA[24]、量子遗传算法（Quantum Genetic Algorithm，QGA）和粒子群算法（Particle Swarm Optimization，PSO）[25]对高海拔风电成本进行优化，优化参数选择为转子半径、轮毂高度和额定功率；优化目标是使LCOE最小化。GA 是一种启发式算法，仿照达尔文生物进化论中自然选择与生物进化的原理。PSO 算法是一种群智能算法，其受鸟类捕食行为的启发。QGA 是在GA 的基础上引入量子的态矢量并以量子门演化替代交叉、变异等操作。

考虑风电机组的轮毂高度、额定功率和转子半径之间存在结构限制，将轮毂高度设置为转子半径的1.5～3 倍，将额定功率设置为转子半径的20～40倍[20]。因此，风电机组成本的数学表达是带不等式约束的非线性寻优问题，考虑结构和设计要求，成本优化问题可以表示为：

各算法参数设定的具体值归纳为表5 所示，表5 中size 为种群规模，T为迭代次数，Pc为GA 的交叉概率，Pm为GA 的变异概率，c1和c2为PSO 的常量，V为PSO 的粒子速度，len 为QGA 的个体量子编码长度。

表5 智能算法参数设定Table 5 Parameters setting of intelligent algorithms

3.1 算法结果分析

3 种智能算法都有其各自不同的实现方式，优化过程也会存在差异。以基准海拔高度2 000 m 情况下的优化结果为例，具体分析不同算法优化下的相应结论。

3 种优化算法最大迭代次数均设置为300 次，LCOE值与迭代次数之间的关系如图1（a）所示。可以看出：使用QGA 算法优化时，LCOE的收敛速度最快，在96 次迭代之后基本收敛。GA 收敛最慢，在经过191 次迭代后，LCOE才基本收敛。PSO 的收敛速度比GA 要快，但比QGA 慢，在经过145 次迭代后基本收敛。LCOE的这种收敛趋势在不同海拔下是相似的。为方便观察，将前100 代的收敛趋势放大并示于图1（b）。

图1 海拔2 000 m处LCOE 优化过程Fig.1 LCOE optimization process at an altitude of 2 000 m

根据图1，采用QGA 算法优化时，经过96 次迭代后，LCOE值收敛到0.049 501 $/kWh。采用PSO算法优化时，经过70 次迭代后达到0.049 502$/kWh，并在145 次迭代后最终收敛到0.049 500 3$/kWh。采用GA 算法优化时，经过100 次迭代后LCOE的值降低为0.049 505 $/kWh，在经过191 次迭代后，LCOE的值收敛到0.049 500 4 $/kWh。这3 种算法均可以有效解决高海拔风电机组的成本优化问题。

使用3 种优化算法优化LCOE时的转子半径R、轮毂高度H和额定功率Pr3 个参数在2 000 m 高度处的收敛趋势如图2 所示：3 种不同的优化算法优化后的参数和LCOE值虽然不完全相等，但最后均收敛到极其相似的结果，误差的数量级达到了10-7。虽然GA 算法的性能不如PSO，但改进后的QGA 算法比其他两种算法具有更好的性能。使用QGA 算法时，在LCOE快速收敛到最优值时，优化参数同样快速收敛到最优解。

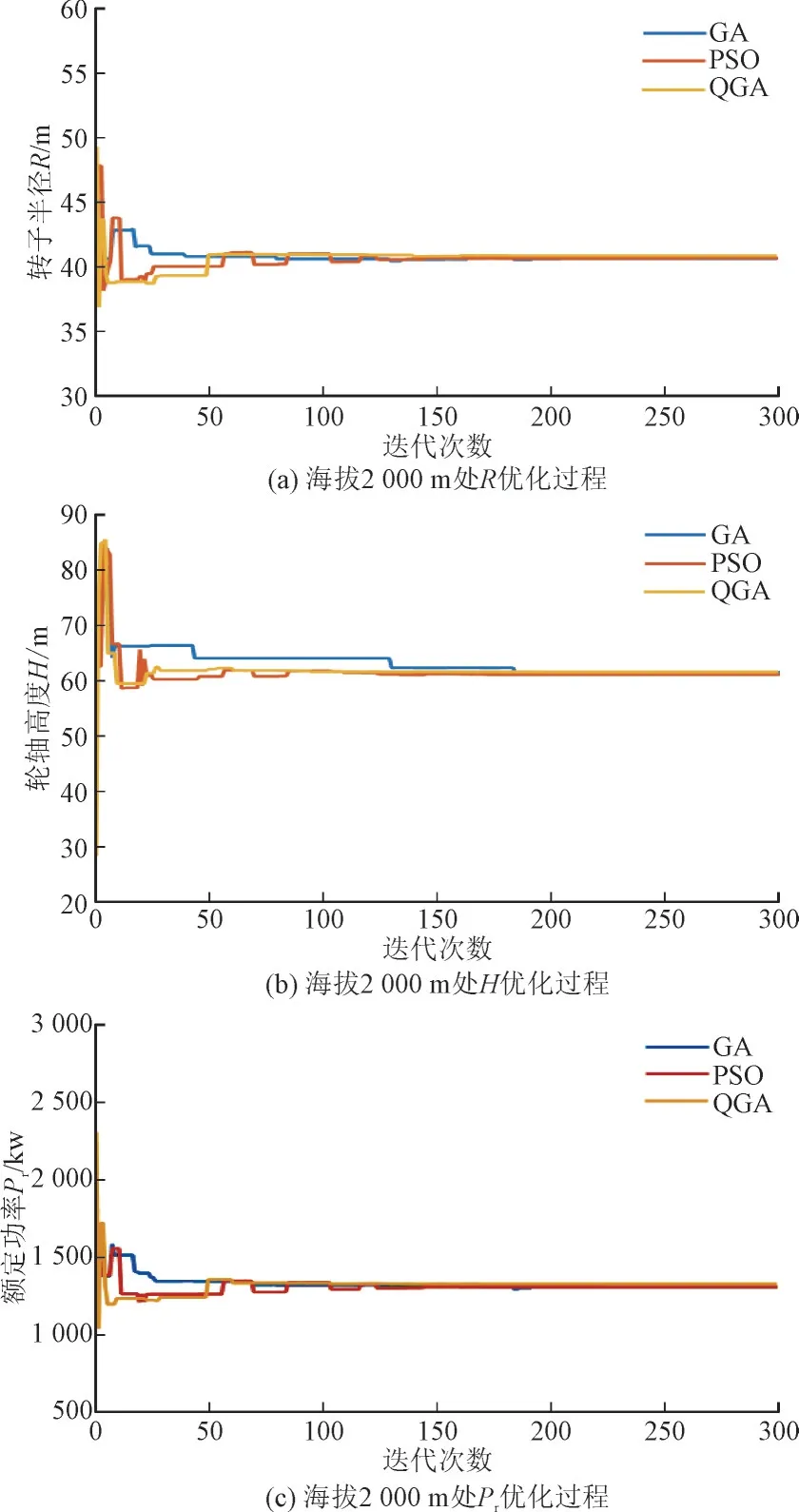
图2 优化参数迭代曲线Fig.2 Optimization parameters iteration curves

结合图1 和图2 可以看出，使用QGA 算法进行96 次迭代后，优化参数已经收敛到最优解；使用PSO 算法进行了145 次迭代后，优化参数收敛到最优解；而使用GA 算法在进行了191 次迭代后，优化参数才收敛到最优解。可以说，当LCOE基本收敛到最优值时，相应的3 个优化参数也同时收敛到最佳值。3 个优化参数在其他海拔高度下的收敛趋势与在2 000 m 处的收敛趋势相似，只是收敛值不同。

3.2 不同高度的最佳参数与最优成本

本文的最终目的是寻找高海拔风电机组的最低风电成本以及对应的风电机组设计优化参数，因此采用不同的优化算法只是为了使结果更加精确。综合比对3 种优化算法在不同海拔高度下的优化结果，可以最终确定最佳转子半径、轮毂高度和风力发电机的额定功率以及对应的LCOE，如表6所示。

表6 不同海拔高度最优LCOE 与最佳参数Table 6 Optimal LCOE and optimal parameters at different altitudes

从表6 可以看出随着海拔的升高，最优LCOE逐渐升高。相关设计参数中，转子半径和轮毂高度随着海拔的升高而增加，额定功率则随着海拔高度的升高而降低。根据这些最优参数可以得到不同海拔下的CAP以及EAP的最优值，如表7 所示。

表7 不同海拔高度最优LCOE，CAP 和EAPTable 7 Optimal LCOE，CAP and EAP at different altitudes

从表7 中可以大致看出，EAP与海拔高度之间应该存在着某种近似线性的关系，EAP随着海拔高度的增加而减小。与基准线处海拔2 000 m 相比，海拔高度为3 000 m 时EAP降低了约5%。而当海拔高度为4 000 m 时，EAP降低了约10%。可以近似认为海拔每升高500，EAP下降约2.5%。相比之下，CAP与海拔高度之间就不存在线性关系，与基准线处海拔2 000 m 相比，海拔高度为3 000 m 时，CAP仅升高了1.7%；当海拔升高至4 000 m 时，CAP仅降低0.3%。可以认为海拔高度对风电机组的影响主要体现在EAP上，其对CAP的影响相较而言非常小。由此可预见，LCOE与海拔高度同样应呈现出类似于EAP与海拔高度之间的负相关关系。

进一步分析，对于EAP与海拔高度呈现这种关系是因为海拔高度的增加导致空气密度的降低，与最优LCOE相对应的最佳额定功率值也相应地降低。尽管转子半径随着海拔高度的增加而增加，但其变化带来的功率正增量不能完全抵消空气密度降低带来的功率负增量，额定功率依然下降，从而导致额定风速的增加。额定风速的增加和额定功率的下降是EAP随着海拔高度的增加而降低的主要原因。而额定风速和额定功率几乎随海拔高度线性变化，导致EAP也随海拔高度的变化而近似线性变化。

同时，对于CAP和海拔高度之间的关系，可以认为两者之间没有直接简单的函数关系。在CAP中，风力发电机的成本随着海拔高度的升高而增加；而运行和维护的成本则随之下降，这主要是由于土地租赁成本的降低。当海拔从2 000 m 上升到3 000 m时，CIC的增加量大于EAO的减少量，导致CAP增加。随着海拔高度的继续增加，CIC的增加趋势变小，而EAO的下降趋势变大，最终EAO的减小量大于CIC的增加量，并导致CAP下降。虽然CAP随海拔高度的变化比较复杂，但变化量很小，因此最终对LCOE影响是EAP为主导。

因此，LCOE的变化趋势与EAP类似，随海拔高度线性变化。在4 000 m 处，LCOE为0.056 208$/kWh，而在2 000 m 处，LCOE为0.049 500$/kWh；与2 000 m处相比，其增加了13.55%。因此海拔每上升500 m，LCOE上升约3.4%。这是因为对于同一风电机组，高海拔地区的低空气密度会导致发电量下降。为了保持相同的产量比，需要增加转子半径，这将导致风力发电机的成本增加。而设计参数的优化也不能完全弥补空气密度降低导致的发电量降低带来的经济损失。并且由于高海拔地区的恶劣地理条件，风力发电机和基础设施的成本增加。这些原因最终导致最优LCOE随海拔高度的增加而增加。

3.3 不同算法优化结果比较

3 种优化算法收敛到相似的值，但还是存在一些差异。在种群规模和迭代次数相同的情况下，采用3 种优化算法得到的不同的海拔高度下的最佳参数和最优LCOE，如表8 所示。

表8 优化参数表Table 8 Optimized parameter table

3 种优化算法获得的最优LCOE值和相应的优化参数非常接近。当海拔高度从2 000 m 增加到4 000 m时，转子半径从40.62 m 变化到了41.67m，而轮毂高度从60.99 m 变化到了62.31m，额定功率从1 307 kW变化到1 218 kW，LCOE从0.049 500＄/kWh 增加到0.052 608＄/kWh。优化设计参数呈现出相同的变化趋势：随着海拔高度的增加，转子半径和轮毂高度增加，而额定功率减小。轮毂高度的升高虽然会导致成本增加，但是其高度的增加带来的风速增量弥补了这一缺点，从而使LCOE降低。而转子半径增大与额定功率减小之间的矛盾是因为空气密度降低导致的功率负增量大于转子半径的增大带来的正增量，从而导致额定功率的减小。

此外，3 种优化算法的原理以及实现方式都有一定的区别，在优化本模型时也存在性能上的差异。为量化比较这种差别从而分辨各算法的优劣，将3 种算法在相同的种群大小以及迭代次数下各运行50 次，将每次运行的平均收敛代数和每次收敛代数记录下来，得到的收敛代数散点图如图3 所示。

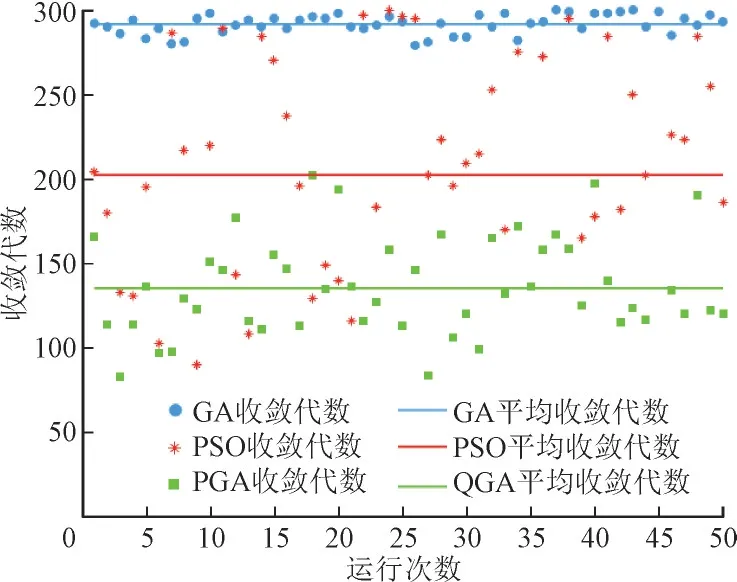
图3 收敛代数散点Fig.3 Scatter points of convergent algebra

从图3 可以看出：GA 算法虽然分布比较稳定，但平均迭代次数达到了292 代。PSO 算法的平均迭代次数为202 代，总体来说比GA 算法提前90 代收敛，但其每次运行的收敛代数不稳定，发散地分布在85 代到300 代之间，且有一次运行至300 代后仍未收敛，陷入局部最优。而QGA 算法的平均收敛代数为135 代，比GA 和PSO 算法的收敛速度快很多，且该算法不存在局部最优问题，每次运行的收敛代数也在平均值附近波动，说明该算法在解决本模型的问题上有着优异的性能。

算法的参数对算法的性能同样会产生影响。表9 显示了在海拔高度2 000 m 时，3 种算法的关键参数变化对算法性能以及优化结果的影响。

表9 不同算法参数下的结果Table 9 Results under different algorithm parameters

从表9 可以看出，算法关键参数的变化对算法或多或少会产生一些影响：

1）对于GA 算法，变异概率和交叉概率增大可以增加种群的多样性，避免陷入局部最优并加快算法的收敛速度，但是算法的运行时间也会增加。在变异概率和遗传概率从0.5 和0.01 变化到0.8 和0.07 时，算法收敛代数从193 代提前到191 代，算法收敛时间从16.3 s 增加到18.7 s。

2）对于PSO 算法，加速度参数的变化对算法的性能并不会产生太大的影响，相对而言鲁棒性更强。在加速度参数从1.194 45 变化到1.964 45 时，收敛时间仅变化0.5 s，且该算法的收敛时间是最快的。

3）对于QGA 算法，关键参数len 对算法有显著影响，显然算法的量子编码长度越长，算法的精确度以及收敛速度越快，但是编码长度边变长也会导致算法在运行时占用的内存过大，运行时间延长。在编码长度从15 变化到25 时，收敛代数提前了13代，收敛时间延长了2.1 s。整体上来说，各算法的参数在合理范围内变化时，算法仍然可以得到模型的最优解，只是在收敛代数以及收敛时间上存在一些差异。

因此，从表8、表9 和图3 可以得出，3 种智能算法都可以很好地解决本文提出的LCOE优化问题。但是，PSO 算法的收敛速度较快，但运行不太稳定，可能陷入局部最优；GA 算法的运行最稳定，但速度也最慢。总体上来说，QGA 算法的性能要优于另外两个算法。

4 结论

本文总结了高海拔地区的气候环境变化，在此基础上建立改进的LCOE 模型，并采用3 种优化算法对模型中的3 个待优化参数—转子半径、轮毂高度、额定功率进行优化并使LCOE的值最低，结论如下：

1）通过将QGA 与PSO 和GA 进行比较，发现QGA 的收敛速度很快。最后的收敛结果也以QGA最为稳定。因此，在本模型的优化中，QGA 算法要优于其他两种算法。

2）随着海拔高度的增加，最佳转子半径值和最佳轮毂高度值增加，最佳额定功率减小，而最优LCOE增大。

3）随着海拔高度的升高，与最佳设计参数相对应的PAE呈下降趋势，而PAC则先上升后下降；海拔高度对PAC的影响小于PAE。

本文仍然还有一些待改进的地方，如改进的LCOE 模型未考虑一些不确定性因素，风力发电成本和土建工作的经济性因素、各种汇率利率等，这些因素可以加入到各部件成本中。