基于转子动能的直驱式风电系统RoCoF下垂控制策略
查雨欣,林 健,张树龙,张 仪
(南京工程学院自动化学院,江苏南京 211167)
0 引言
新能源和分布式发电作为缓解能源危机的重要途经,近年来得到了迅速发展[1-5]。其中,风力发电因其技术成熟、成本低廉、易于大规模开发利用,已成为发展最快、规模最大、最具竞争力的新能源发电技术。风力发电主要采用的是直驱永磁同步发电机(Direct-drive Permanent Magnet Synchronous Generator,D-PMSG),其结构简单、维护成本低、转速可调、效率高、控制灵活[6-12]。
D-PMSG 正常运行时,机组按照最大功率跟踪(Maximum Power Point Tracking,MPPT)控制运行,其转子转速和输出功率与电网频率变化无关,即基于全功率变流器进行控制的风力发电系统是与电网频率响应解耦运行的,系统的频率稳定只能依靠自身的惯量。
因此,一些国家和地区的电网中风电机组占比提高,势必会削弱系统的整体惯性,进而更容易在负荷扰动后产生较大的频率波动,偏离工频会导致频率偏差或者频率变化率(Rate of Change of Frequency,RoCoF)过大,其量值为RCF,极易引发全网频率事故。世界主要风电发达国家与地区对风电的调频能力进行了规范,并提出了明确要求[13-14]。
为了使风机能够为电网提供辅助惯量,改善系统惯量特性,以降低系统的频率波动,文献[15-17]提出了虚拟同步发电机(Virtual Synchronous Generator,VSG)控制,使得并网逆变器具有一定的惯量特性,但VSG 控制结构相对复杂。文献[18]分析了虚拟惯量控制策略中比例微分控制PD 参数的控制规律,为虚拟惯量控制参数整定提供理论依据。文献[19]利用电容释放能量的快速性原理,通过耦合RoCoF 和母线电容电压,在扰动产生时快速释放电容能量来补偿系统不平衡功率。文献[20]加入储能环节,提出了一种适用于风储交流微电网在离网运行模式下的自动功率平衡控制策略,建立了发电、储能和负荷间的协调功率调控机制,但是这种控制方法增加了设备,提高了控制成本。在研究风力发电系统的惯量特性时,文献[15-20]侧重于并网逆变器以及直流侧电容的动态特性,而没有考虑风机转子机械动能。在文献[21]中,频率偏差由PD控制,并产生辅助指令Pvic,该指令可调动风机转子动能以响应电网中的频率变化,从而为系统提供惯量支撑。文献[22]研究了PMSG 风力发电机在暂态过程中支持系统惯性的两种新的控制策略,通过同时利用或者级联控制直流电容容量和风机转子动能,从而为系统提供惯量支撑;但是无论是哪种控制,风机的输出都没法回到最大功率输出,系统在非额定工作状态下长期运行,降低了风力发电的经济性。
因此,本文在不增加额外设备的前提下,对风机转子暂态过程进行了分析,利用风机转子的动能来抑制RoCoF,提出一种基于有源低通滤波器(Low-pass Filter,LPF)的RoCoF 下垂控制策略,将微电网的RoCoF 与风机转子动能耦合,在扰动产生时,利用RoCoF 的快速响应特性将转子中的裕量用以微电网的平衡。最后通过仿真分析验证了系统惯量特性分析的正确性。
1 虚拟惯量控制
1.1 风机转子能量的利用
文献[23]提出了多尺度特性划分原则,根据系统不同结构的动态响应时间可分为机电时间尺度(秒级)和电磁时间尺度(毫秒级),后者又分为直流电压控制尺度(约100 ms)和交流电流控制尺度(约10 ms)。由于关联机电暂态过程,直流电压时间尺度的动态过程较机电过程略快,涉及能量也较大。交流电流时间尺度覆盖了交流系统电阻、电容、电感等电磁元器件的电磁变化过程,与机电时间尺度和直流电压时间尺度相比,电磁时间常数小,储能水平极低[24-25]。
在大时间尺度作用下,风机转子储存了相当可观的能量。在有限能量约束条件下,若能利用这部分能量,那么风力发电系统也可以为电力系统提供一定量的惯量支撑,以有效减少对电网储能容量的需求。
为了使直驱式风电机组拥有与传统同步发电机组相近的频率支撑能力,抑制电网振荡,主要有2大类控制方法,分别是惯量控制和阻尼控制(下垂控制)。惯量控制通过增强电力系统的惯性水平来抑制频率变化率dω/dt;下垂控制通过增强电力系统的阻尼能力来抑制频率差值Δω。
图1 所示为风机并网发电系统的典型结构。风力机通过传动轴与D-PMSG 的转子相连,捕获到的风能由全功率变流器控制、变换后,经升压变压器接入电网。其中,Pwind为风机捕获到的风能,PWT为PMSG 输出的动能,Pg为电网功率;VDC为直流母线电压;isabc,igabc分别为整流器输入电流和逆变器输出电流,isd,isq,igd,igq分别为整流器和逆变器经过abc转dq后的电流大小;θr为风机转子位置信息,ωr为θr求导后的转速大小;Lw,Lg分别为整流器滤波电感和入网前的滤波电感。
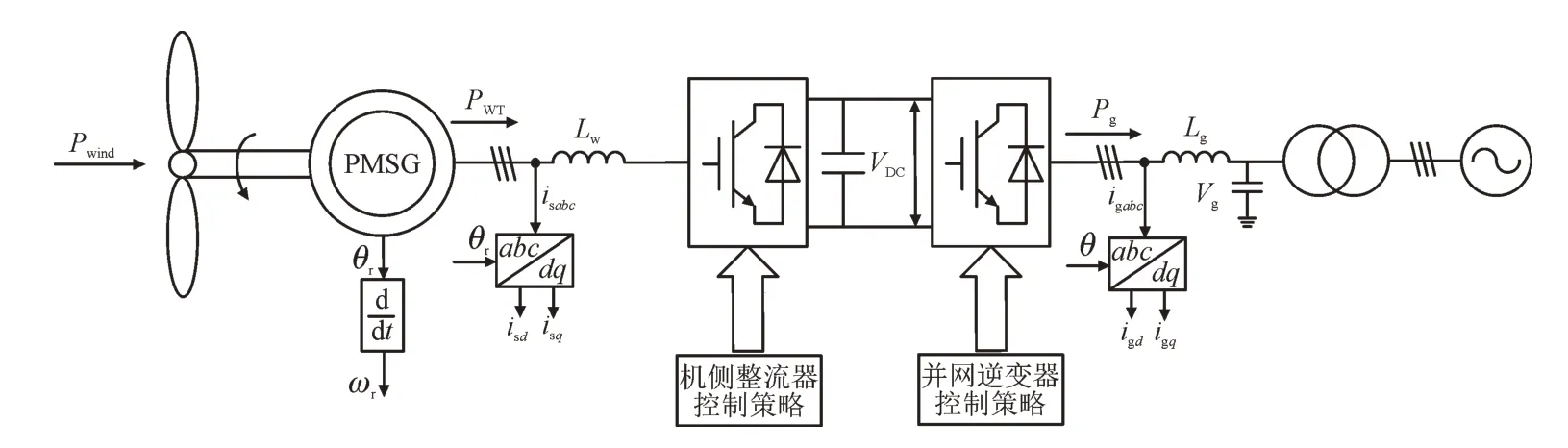
图1 直驱式风力并网发电典型结构图Fig.1 Typical structure diagram of direct-drive wind grid-connected power generation
1.2 PD虚拟惯量控制存在的问题
在D-PMSG 的MPPT 控制基础上引入辅助指令Pvic,其控制原理结构图如图2 所示。其中,Pw为同步发电机的实际输出功率,PMPPT为MPPT 控制下的参考输入功率,f0为额定频率,f为实际电网频率,kopt为使风机达到最大功率的系数,s为微分算子,kp为虚拟惯量P 控制器系数,kd为虚拟惯量D 控制器系数,为isd,isq的给定信号,SPWM 为正弦脉宽调制。

图2 PD虚拟惯量控制理图Fig.2 PD virtual inertia control diagram
PD 虚拟惯量控制下的辅助功率指令为:
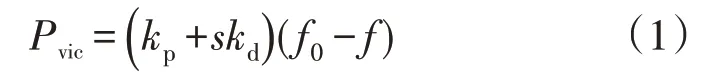
在虚拟惯量控制下,忽略电磁损耗后风机的输出功率为:

无负荷扰动情况下PMSG 采用MPPT 控制,风机的输出功率为:
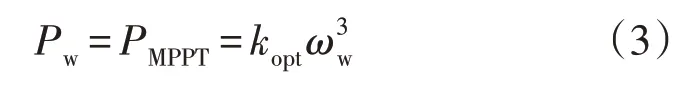
系统频率由电网输出功率PG、负荷功率PL、同步发电机输出功率Pw共同决定,即:

式中:H为电网的等效惯性常数。
负荷发生扰动后,电网本身的频率特性也将对系统频率变化做出反应:

式中:TD为电网的等效阻尼系数,且TD越大,电网的频率调整(FR)能力越强;PG0为系统受扰前的原动机出力;PFR为电网的主频率响应;PL0为受扰前的负荷;ΔPL为扰动量。
系统未受扰动前,PMPPT0、PG0和PL0满足:
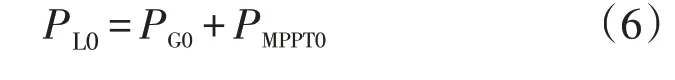
式中:PMPPT0为受扰前的最大功率输出。
在负荷扰动初期,由于电网调速系统不灵敏区的存在以及调速系统响应速度的限制,高风电渗透率电网的频率变化在负荷扰动后瞬间达到最大值,在此短间隔内,可认为系统的主频率响应不起作用PFR=0,同时在扰动初期,由于风机风速不会迅速下降,可认为风机的PMPPT等于PMPPT0。
假设系统在扰动发生前以额定频率运行,扰动发生后,结合式(1)—式(6),系统的频率变化方程为:

由式(7)可知,在虚拟惯量控制下,提高kd和kp可以分别提高系统的等效惯量和阻尼系数,等效增加了系统的惯量和阻尼。由式(7)可得风机并网系统频率的变化方程为:

忽略风机的机械阻尼,PMSG 传动系统的转动方程可以表达为:

式中:PWT为风机的机械出力;Jw为风机的等效转动惯量;Tw为风机的机械转矩;Te为风机的电磁转矩。将式(1)、式(2)带入式(9),联立方程可得:

为简化分析,可忽略PWT的变化,假定风机的机械出力等同于风机在MPPT 控制下的输出功率,即有:
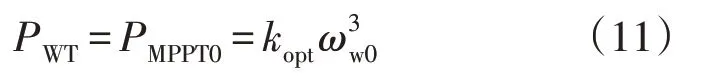
将式(11)带入式(10),可得:

当风机到达稳态时,dωw/dt=0,df/dt=0,可得稳态时风机转速为:
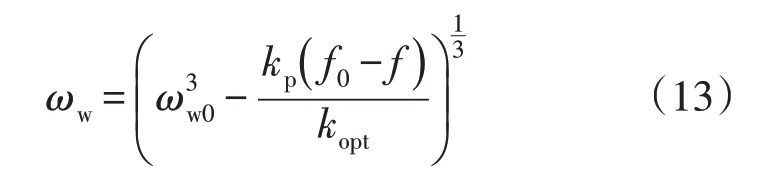
由式(13)可知,高风电渗透率电网随着虚拟惯量控制参数kp的增加,在受到负荷扰动后,风机转速会明显下降,越发偏离风机最大功率点,并且在扰动结束后的稳态风速不能恢复至最大风速点。由于参与系统频率响应只是D-PMSG 机组的辅助任务,核心任务是满足电网发电需求,风机若频繁动作响应电网频率变化,容易造成风机叶片的机械疲劳,增加风机的维护成本。因此,在保证系统频率满足电网规程要求的前提下,虚拟惯量控制应尽量减少辅助功率出力,实现风能的最大利用,保障D-PMSG 机组并网发电的经济性,不宜通过极限偏离PMPPT、深度降低转子转速的方式来进行频率支撑。
2 直驱式风电系统RoCoF下垂控制
为提高D-PMSG 机组并网发电经济性质,减少风机维护成本,本文提出一种基于LPF 的RoCoF 下垂控制策略,利用RoCoF 的快速性原理调动转子的能量为系统提供惯量支撑。
图3 为机侧的RoCoF 下垂控制策略框图,工频频率f0与电网频率f作差,得到频率偏差Δf。通过调节LPF 的带宽ωc,消除其中所包含的高频噪声,使逆变器主要在低频信号上响应,经过微分环节得到系统的RoCoF,再利用下垂系数Kd将得到的信号经过放大后得辅助指令Pvic:
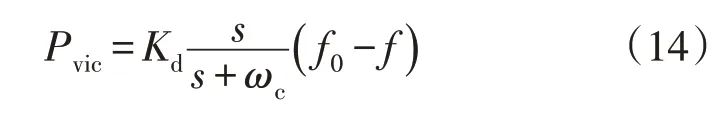
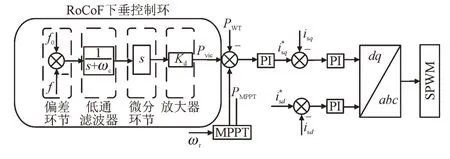
图3 机侧RoCoF下垂控制变流器控制策略Fig.3 Control strategy of generator-side RoCoF droop control converter
将式(14)替代式(1)带入式(9)可得:
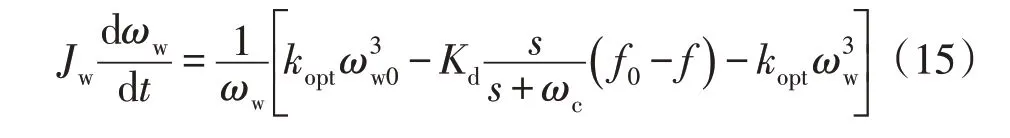
在系统到达稳态时,dωw/dt=0,df/t=0,整理式(15)可得风机最终转速为:

由式(16)可知,系统在基于LPF 的RoCoF 下垂控制策略下,风机的转速在扰动后到达稳态时能回到初始转速。该控制策略可将风能利用最大化,保障D-PMSG 机组并网发电的经济性。与此同时,相较于频率偏差,在扰动时通过RoCoF 也能提供更大的惯量支撑,减少风机叶片的频繁动作,减小风机损耗及维护成本。
3 仿真分析
在Matlab/Simulink 仿真平台上搭建直驱式风力发电并网模型,对系统惯量特性进行分析,实验验证基于转子动能的直驱式风电系统RoCoF 下垂控制的有效性。仿真系统主电路结构如图1 所示,变流器的控制方法如图3 所示。
仿真工况设置:起始时刻,由风力发电系统与微电网共同承担40 kW 的负荷,在1.5 s 时增加负荷20 kW,风电系统的主要参数如表1 所示。

表1 风电系统的主要参数Table 1 Main parameters of wind turbine system
3.1 不同控制策略的仿真效果
为了验证基于LPF 的RoCoF 下垂控制的有效性,仿真了直驱式风力系统在有无虚拟惯量控制下的运行情况,并对比PD 控制和RoCoF 下垂控制对风机输出和电网频率的影响,结果如图4 所示。

图4 不同控制策略对系统的响应Fig.4 Response of different control strategies to the system
由图4(a),(b),(c)可知,尚未采用虚拟惯量控制时,即在电网频率耦合至风机侧之前,1.5 s 增加电网侧负荷产生扰动时,机侧的风机转速并不响应扰动而发生变化,电网输出恒功率,风机的转子也不响应。因此在使用不耦合电网频率的控制策略时,电网频率变化率也会高于其他2 个控制策略(如图4(d))下的频率变化率。相反地,加入电网频率的偏差(或频率变化率)后,在1.5 s 负荷增加时,电网频率及风机转速做出了相应的变化,风机的转子释放其动能,扰动产生时,风机的输出功率提高,为系统提供了惯量支撑。从图4(d)可以看出,相比无虚拟惯量,加入虚拟惯量控制后,电网频率变化率变小,即系统的惯量得到提升,而RoCoF 下垂控制比PD 虚拟惯量控制对扰动的响应更迅速。由图4 可知,相比于PD 虚拟惯量控制,RoCoF 下垂控制对扰动的响应更快,网侧的频率变化率更低。因此可以说,RoCoF 下垂控制可以控制风机转子为系统提供更多的惯量支撑。
3.2 不同控制参数的仿真效果
下面具体分析RoCoF 下垂控制中放大系数和截止频率的参数对系统运行的影响规律,为更好地设计控制器参数提供理论支撑。
在保持系统各参数不变情况下,Kd分别选择50 000,80 000,100 000,风机输出功率、电网频率变化率、电网输出功率及风机转速的变化规律如图5所示。由图5 可以看出随着Kd参数变大,在扰动时风机转速下降越多,即风机转子释放的能量越多,为系统提供的惯量支持越多,除此之外响应速度也随着Kd增大而提高(如图5(a),(b))。对应到电网侧如图5(c),(d)所示,Kd参数越大,电网功率也随之增大,且在稳定电网频率方面,RoCoF 的值越小,系统更加稳定。

图5 不同放大系数Kd对风机并网系统的影响规律Fig.5 Influence law of amplification factor Kd on wind turbine grid-connected system
同样地在保持系统各参数不变情况下,改变RoCoF 下垂控制中LPF 的截止频率。ωc以50,100,200 倍增,其对风机输出及电网的影响效果如图6所示。由6(a),(b)可知,ωc越小,风机对扰动的响应则越强,输出的转子释放的能量也随之增加。与此同时,如图6(c)所示电网功率响应变化增强,逆变器快速响应能力得到提高,系统的惯量水平随着ωc减小而增强。截止频率ωc变小,RoCoF 的值也随之变小,说明截止频率ωc越小,逆变器抑制RoCoF的能力越强(如图6(d))。相反地,若截止频率ωc越大,功率控制环中混入高频噪声就会不利于系统频率的稳定。

图6 不同截止频率ωc对风机并网系统的影响规律Fig.6 Influence law of cut-off frequency on wind turbine grid-connected system
4 结论
本文提出的基于LPF 的RoCoF 下垂控制策略可通过利用风机转子动能使D-PMSG 在满足电网频率阈值标准条件下经济运行,改善电网RoCoF。通过对风电系统的分析,对比了有无下垂控制、常规PD 虚拟惯量控制和RoCoF 下垂控制策略对风电系统的影响,以及下垂控制控制参数的影响规律。结果表明:
1)通过在风机侧加入下垂控制,可以利用转子中储存的备用裕量快速补偿系统缺额功率,因此相比于常规控制,下垂控制可调动风机侧的转子能量,风机侧可以响应电网侧的频率变化。其次,相比于PD 虚拟惯量控制,RoCoF 下垂控制策略可在增加负载扰动下,更好地抑制频率变化率过大问题,并在进入新的频率稳态时,又能够恢复转子释放后的这部分备用容量,使得风机不用长时间保持在新的稳态。
2)D-PMSG 系统的惯量特性受控制策略中控制参数的影响,通过增大放大系数Kd或减小截止频率ωc可从转子中获取更大的惯量,从而提高微电网惯性水平。

