方差性质的应用及拓展

⦿甘肃省天水市秦安县第二中学 任亚丽

1 方差的性质

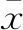
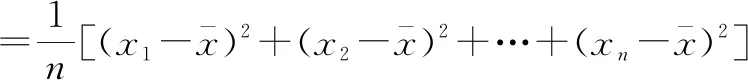
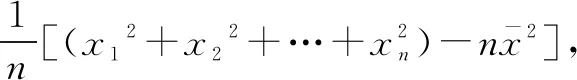
由方差定义公式，容易得出方差的两条性质.

性质1：S2≥0，即任何一组实数的方差都是非负实数．

性质2：当且仅当x1=x2=…=xn时，S2=0，即若一组实数数据的方差为零，则该组每个数据均相等，且都等于该组数据的平均数．

运用这两个性质和方差计算公式，常可帮助我们快捷解决一类与之相关的问题．

2 方差性质的应用

2.1 求值

例1已知x+y=8，xy-z2=16，求x+y+z的值．

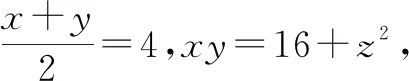
所以x，y的方差为

由性质①，得-z2≥0，所以z2≤0.

z2=0，即z=0，所以s2=0.

由性质②，得x=y=4.所以x+y+z=4+4+0=8．

2.2 求最值

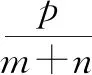
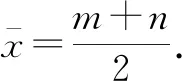
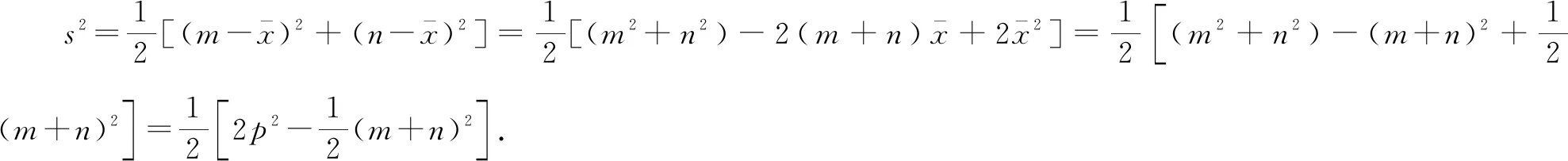
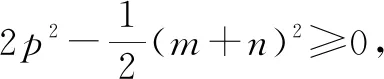
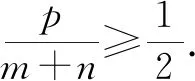
2.3 证明不等式

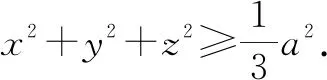
证明：设x2+y2+z2=ω，由方差公式，得x,y,z的方差为

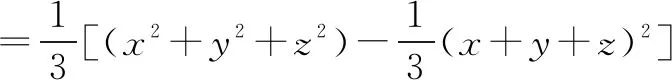
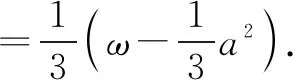
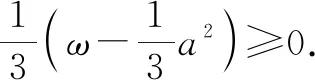
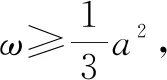
2.4 证明等式

例4已知实数a,b,c满足a=6-b，c2=ab-9，求证：a=b．

证明：由已知得a+b=6,则

a2+b2=36-2ab=36-2(c2+9)=18-2c2.

由方差公式，得实数a,b的方差为

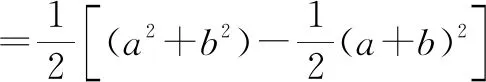
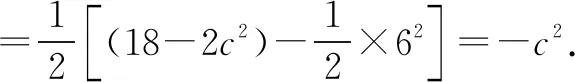
因为s2≥0，所以-c2≥0.

所以c=0，因此s2=0，则a=b.

2.5 解方程

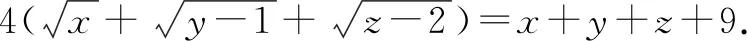
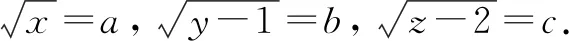
则x=a2，y=b2+1，z=c2+2，原方程可化为4(a+b+c)=a2+b2+c2+12.

所以a2+b2+c2=4(a+b+c)-12.

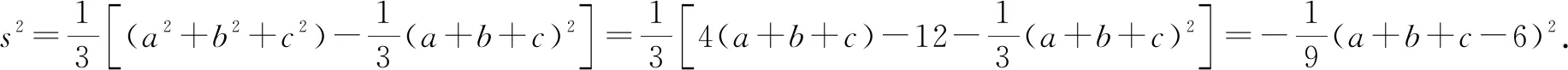
因为s2≥0,所以(a+b+c-6)2≤0.因此a+b+c=6.于是s2=0,a=b=c=2.

所以x=4,y=5,z=6.经检验，x=4,y=5,z=6是原方程的解.

2.6 判断三角形形状

例6设△ABC的三边a,b,c满足：b+c=8，bc=a2-12a+52，试问△ABC是什么三角形(按边分类)？并证明你的结论.

解：△ABC为等腰三角形，证明如下：

由已知得b2+c2=64-2bc=-2a2+24a-40.

由方差公式,得b,c的方差为

因为S2≥0，所以-(a-6)2≥0，即a=6，于是S2=0.

所以,b=c=4.

故△ABC是以a为底，以b,c为腰的等腰三角形.

3 引伸与推广

证明：n个数a1,a2,a3,…,an的方差为

因为S2≥0，所以

该定理反映了“n个数的平方和”与“n个数的和的平方”之间的内在联系.

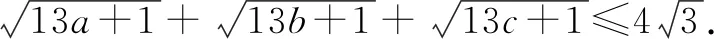
证明：由定理知

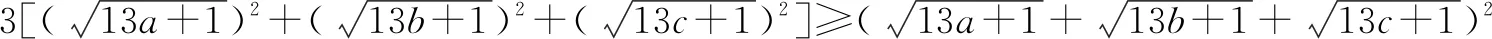
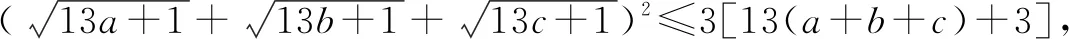
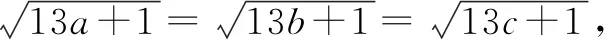
4 结语

由上面几道例题我们可以知道，方差中的大多数问题都是利用方差大于零或者是方差等于零时建立等式与不等式(即方差的非负性)来作为突破口解决的.方差性质的运用往往能使同样的一道题由繁变简，由难变易，并能快速求解.