一道教科研联盟函数题的破解
⦿安徽省利辛县第一中学 李晓兰
1 引言
导数法是处理直线与曲线的位置关系、函数的零点、方程的实根等相关问题的基本方法.根据题目情境的巧妙设置,合理变形与转化,通过函数的构建,结合求导处理,借助函数的单调性等基本性质,通过基本函数的图象与性质来合理转化,巧妙破解,已经成为高考、联赛等命题的高频考点之一,倍受关注.
2 问题呈现
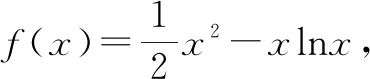
此题以含参的直线与曲线的位置关系为问题情境来创设,借助导数来研究函数的零点问题,通过导数研究函数的单调性,利用数形结合、分类讨论、参变分离或构造方程法等思维方法来分析与处理,难度较大,创新新颖,具有很好的区分度.
3 问题破解
方法1:数形结合法.
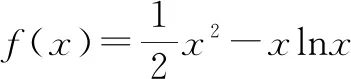
令函数g(x)=x-lnx-1,求导可得
当0 当x>1时,g′(x)>0,g(x)在区间(1,+∞)上单调递增. 所以g(x)min=g(1)=0,故g(x)≥0在区间(0,+∞)上恒成立. 所以f(x)在区间(0,+∞)上单调递增. 图1 作出函数f(x)的大致图象,如图1所示. 点评:破解的关键是利用导数研究函数f(x)的图象,数形结合来确定参数b的取值范围.由于函数f(x)的图象非熟知,结合导数法,利用求导处理并通过研究函数的单调性来大致确定函数的图象,为破解问题的数形结合思想提供图形依据.数形结合法是处理此类问题的常用方法,借助函数图象为突破口,采用数形结合思想,比较巧妙. 方法2:分类讨论法. (1)当b<0时,g′(x)有唯一零点x0,g(x)在区间(0,x0)上单调递减,在区间(x0,+∞)上单调递增. 而当x→0+时,g(x)→+∞;当x→+∞时,g(x)→+∞. 所以g(x)min=g(x0)=x0-lnx0+1-k,而取k=1时,g(x)无零点,舍去. (2)当b=0时,g′(x)有唯一零点2,g(x)在区间(0,2)上单调递减,在区间(2,+∞)上单调递增. 而当x→0+时,g(x)→+∞;当x→+∞时,g(x)→+∞. 所以g(x)min=g(2)=1-ln2-k,而当k<1-ln2时,g(x)无零点,舍去. 而当x→0+时,g(x)→-∞;当x→+∞时,g(x)→+∞,满足要求. 而当x→0+时,g(x)→-∞;当x→+∞时,g(x)→+∞. 所以,存在k∈R,使g(x1)>0,g(x2)<0,此时,g(x)有两个零点,舍去. 点评:通过直线与曲线的位置关系对条件进行合理的转化,巧妙构建对应的方程,通过方程的变形与转化,构建对应的函数,通过求导处理,利用参数取值的分类讨论,确定在每种情况下函数零点的情况,从而得以确定参数的取值范围问题.分类讨论法能很好地处理双参数问题,寻找结论成立的条件,不重不漏,严格缜密,只是过程比较繁杂,讨论细节较多,容易导致错误,要引起注意. 方法3:参变分离法. 根据题意知,对任意实数k,都有唯一的x与之对应,则可知函数g(x)是单调函数. 令函数h(x)=x2-2x+2b,可知函数h(x)是开口向上的二次函数. 点评:通过直线与曲线的位置关系对条件进行合理的转化,巧妙构建对应的方程,借助参变分离,构建对应的函数,结合函数的定义以及单调性的定义,将问题转化为相应函数的单调性问题,通过求导,借助二次函数的图象与性质,通过判别式小于等于0来建立不等式,进而确定参数的取值范围问题.参变分离法是破解涉及函数参变量问题中比较常用的一种技巧方法,利用参变分离进行等价转化,转变问题视角,巧妙分析与破解. 方法4:构造方程法. 令函数h(x)=x2-2x+2b,可知函数h(x)是开口向上的二次函数. 点评:通过直线与曲线的位置关系对条件进行合理的转化,巧妙构建对应的方程,通过方程的变形与转化,构建对应的函数,通过求导处理,借助二次函数的图象与性质,通过判别式小于等于0来建立不等式,进而得以确定参数的取值范围问题.构造方程法合理综合与分类讨论法与参变分离法的优点,巧妙组合,优化过程,提升效益. 探究1:通过保留题目条件,适当改变对应的函数解析式与参数条件,可以得到以下对应的变式问题. 下面先证明g(x)<1恒成立. 假设∃x0∈(0,+∞),使得g(x0)≥1.因为x→0+时,g(x)→-∞,且当自变量x充分大时,g(x)<1, 所以存在x1∈(0,x0),x2∈(x0,+∞),使得g(x1)<1,g(x2)<1. 取k=max{g(x1),g(x2)}<1,则y=k与y=g(x)至少有两个交点,与题意矛盾. 由对任意k∈(-∞,1),g(x)=k只有一个解,得g(x)为(0,+∞)上的递增函数. 因此b≥m(x)max=m(2)=-ln2,即b的取值范围是[-ln2,+∞). 故填答案:[-ln2,+∞). 通过研究函数图象的交点问题,以导数为工具研究函数的单调性,多参数立意新颖,任意类恒成立问题与基本概念密切联系,深入浅出地考查学生的数学运算、逻辑推理等核心素养.关于本题的处理方法,我们经常采用数形结合、分类讨论、参变分离、构造方程等方法,其中数形结合直观,分类讨论周密,参变分离快捷,构造方程优化,都是非常好的分析与处理此类问题的基本方法. 导数法是分析与解决函数的零点、方程的实根等相关问题中比较常用的一种技巧方法,也是借助导数法来考查此类问题的热点与难点之一.通过函数的零点、方程的实根、直线与曲线之间的交点个数等不同情况来合理创设问题,背景设置各异,变化多端,求解的形式与方法也各不相同.熟练掌握基本题型,把握问题实质,以不变应万变,全面提升数学品质,提高数学能力.Z
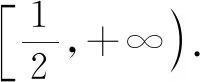
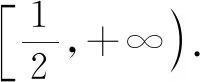
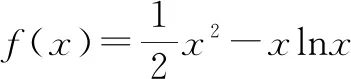
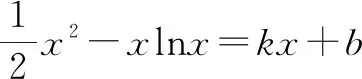
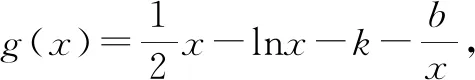
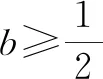

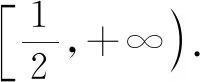
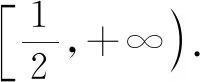
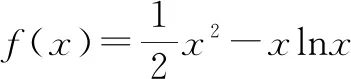
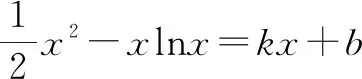
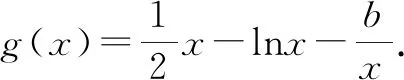
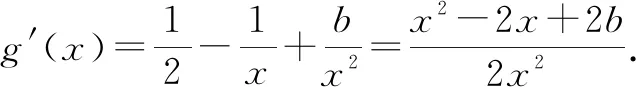
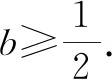
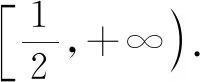
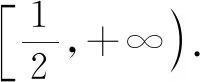
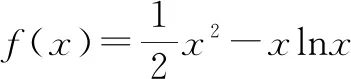
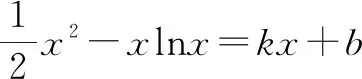
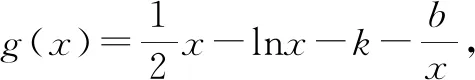
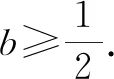
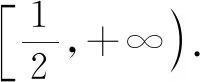
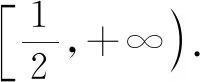
4 变式拓展
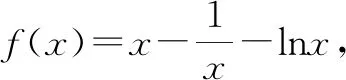
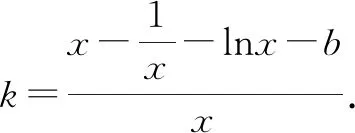
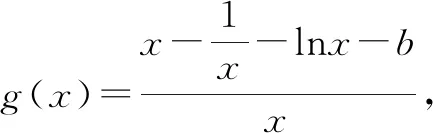
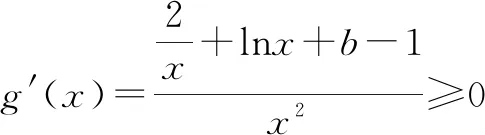
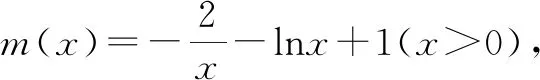
5 教学启示
5.1 方法总结,技巧归纳
5.2 考点剖析,能力提升

