2021年高考数学全国甲卷(理)第9题的多角度破解及拓展

⦿湖北省武汉市常青第一中学 谌述涛

1 引言

三角函数式的化简与求值问题一直是高考数学命题的一个基本题型，考查形式各样，背景设置多变，有时单独设置问题考查，有时交汇融合其他知识辅助考查，有时作为基本过程合理过渡等，常考常新，可以很好考查数学抽象、逻辑推理、代数运算等方面的数学能力与核心素养等．

2 真题呈现

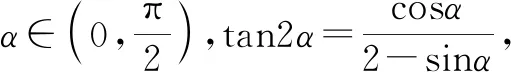
3 真题剖析

该题条件简单，短小精悍，难度适中，以三角函数中单角、倍角的三角函数式来设置条件，求解单角的正切值，综合考查三角恒等变换、同角三角函数基本关系式等相关知识．

正确进行三角函数求值的关键就是化同角，巧变换，妙求值．具体破解时，可以从条件中的三角关系式入手，或三角恒等变换处理，通技通法；或三角函数定义处理，回归本源；或数形结合处理，解几直观等．结合不同的思维视角与方法来处理与求值，很好地考查考生对三角函数综合知识的理解与掌握程度，更深层次上强化思维的灵活性、多样性、拓展性等．

4 真题破解

方法1：通技通法思维——三角恒等变换法.

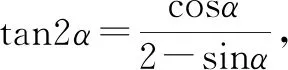
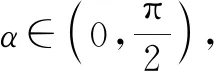
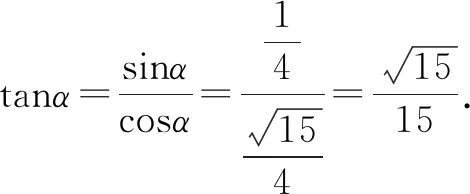
点评:常规思维中，将已知等式左边“化切为弦”，利用二倍角公式“化同名”，得以求解sinα的值，进一步利用三角函数中的平方关系求得cosα的值，最后由三角函数中的商数关系即可得tanα的值．利用三角恒等变换法处理三角函数中的求值问题，是破解此类问题的通技通法，注意三角函数公式的巧妙转化与应用．

方法2：回归定义思维——三角函数定义法.

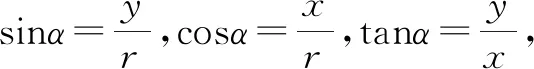
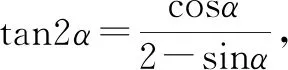
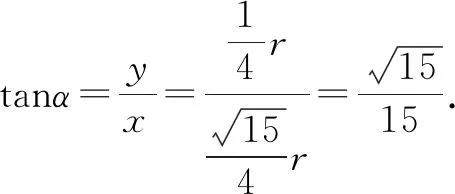
点评:结合三角函数的定义，将三角函数转化为参数x，y，r之间的关系式，通过二倍角公式转化原来的三角关系式，结合三角函数定义代入，并对参数进行变形与化简，建立对应参数之间的关系，进而利用定义确定对应的正切值．利用三角函数定义思维来破解三角函数的求值问题，回归问题本质，也是破解三角函数求值中比较常见的一类技巧策略．

方法3：数形结合思维——解析几何法.

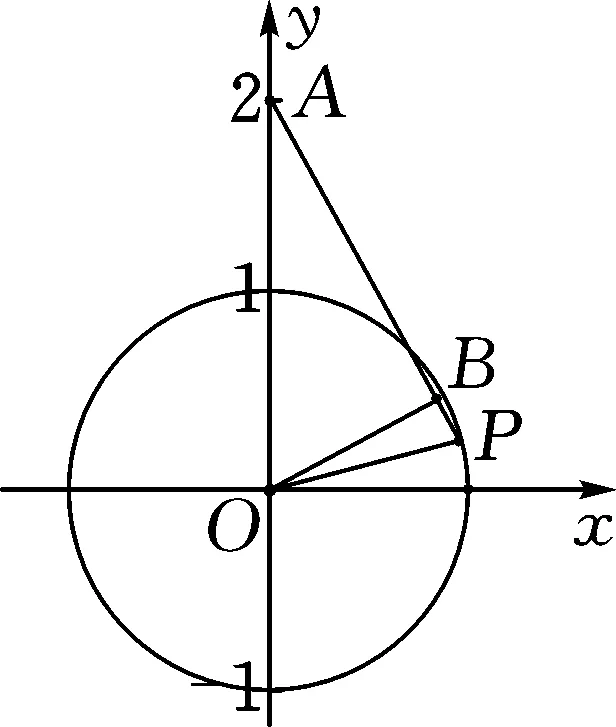
图1

解析：如图1所示，在平面直角坐标系xOy中，A(0，2)，点P(cosα，sinα)在单位圆x2+y2=1上，点B在直线AP上，从而∠POx=α，设∠BOx=2α.

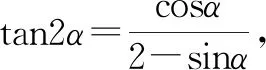
所以∠POx=∠BOP=α，∠OAB=∠BOx=2α，∠OPA=90°-α.

在△AOP中，|OB|=|OA|sin2α=|OP|sin(90°-α)，则有2sin2α=sin(90°-α).

整理可得4sinαcosα=cosα.

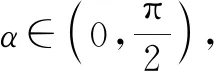
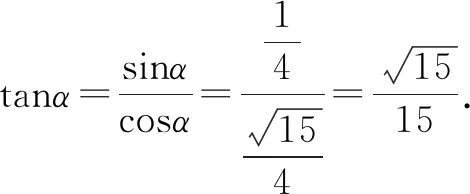
点评:数形结合思维中，抓住已知三角关系式的特征，建立平面直角坐标系，将已知的关系式转化为两直线的斜率之积为-1的关系，进而化“数”为“形”，借助两直线的垂直，通过平面几何的直观形象，利用解直角三角形建立相应的关系式，得以确定sinα的值，进一步利用三角函数中的平方关系求得cosα的值，最后由三角函数中的商数关系即可得tanα的值．利用数形结合思维来直观想象，是一种不错的技巧方法，要求准确识破条件中三角关系式的特征，可以作为我们学习的一个拓展与延伸．

方法4：数形结合思维——平面几何法.

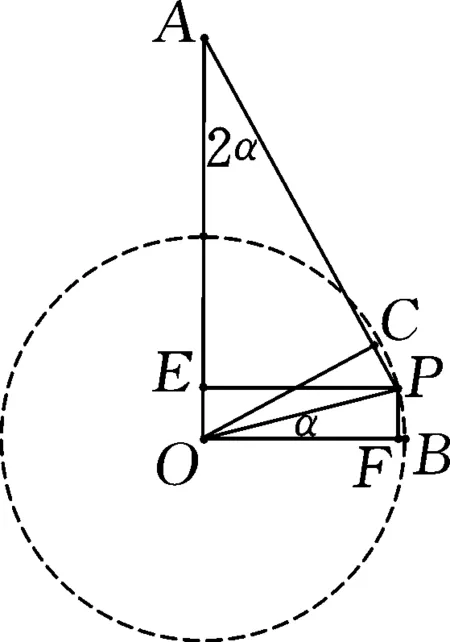
图2

解析：如图2所示，点B，P在单位圆O上，且OA⊥OB，|OA|=2，∠POB=α.

四边形OFPE为矩形，点C在直线AP上，且∠POC=∠POB=α.

则有|PE|=|OF|=cosα，|OE|=|PF|=sinα，可得|AE|=2-sinα.

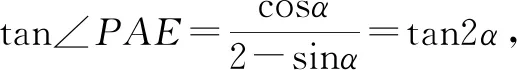
而∠PAE=2α=∠COB，则知∠ACO=∠AEP=90°，且|OC|=|OF|=cosα.

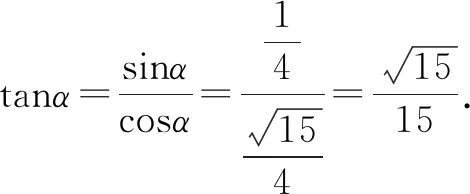
点评:巧妙构建对应的平面几何图形，利用几何图形中边与角的关系，并结合解直角三角形加以合理转化与应用．过程比较繁杂，巧妙构建单角与双角之间的联系，以及对应的三角函数值之间的比值与转化，数形直观，逻辑推理．平面几何图形的变化多端，对于我们来说也是一个很好的拓展与延伸．

5 变式拓展

对于三角函数式的化简或求值问题，在其他高考试卷中也有类似的真题，与以上问题刚好相反，通过单角的正切值，来求解涉及单角、双角的三角函数式的值问题．

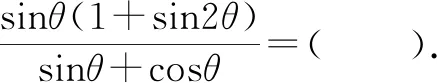
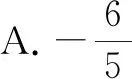
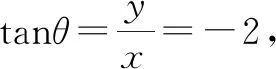
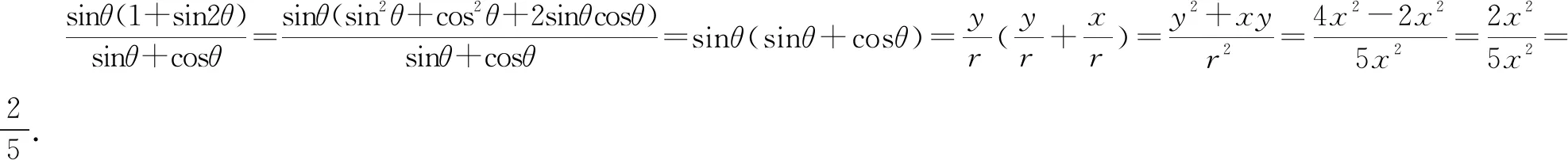
点评:对于该问题的破解，可以通过三角关系式的齐次化思维、统一思维、各个击破思维以及三角函数定义思维等方式来处理，结合不同的思维方法来处理与求值，都可以达到破解的目的．

6 教学启示

6.1 掌握通技通法，熟记基本公式

在进行三角函数式的化简或求值时，一定要掌握最常见的三角恒等变换法，对三角函数式进行切化弦、化同名、化同角等常规处理，掌握破解问题的通技通法，前提条件就是熟练记忆三角函数中的一些基本公式，方便灵活应用，巧妙变换．在实际教学过程中，要督促学生对基本公式的理解与记忆．

6.2 回归定义本源，类比几何本质

三角函数问题是建立在三角函数定义的基础上，往往回归三角函数的定义本源，问题也可以得以很好处理；同时三角函数更是初中平面几何基础上的拓展与延伸，离不开几何本质与图形特征．在实际教学过程中，要适当渗透三角函数定义的本源回归，以及平面几何本质的数形结合与直观应用．Z