一道全国高中联赛向量题的探究及拓展

⦿贵州省湄潭县湄江高级中学 杨 滔

1 引言

平面向量的最值问题一直是高考中非常常见的题型之一，可以涉及平面向量的模、夹角、数量积、参数值等多个要素，也是各类模拟卷、自主招生、竞赛中比较常见的题型．平面向量的最值问题往往切入点多，方法多样，而且难度一般都不低，是一个数学知识融合，创新意识应用，数学能力提升以及数学核心素养培养等的重要场所．

2赛题呈现

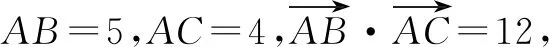
此题以三角形为载体，结合三角形的边长与两向量的数量积来确定已知的三角形，利用动点P的“动”态，结合数量积的“数”式，利用平面向量的线性运算与数量积运算来合理转化，进而形成“形”式，确定“静”态情况下相应的最值问题，创新性强，让人眼前一亮．

3 问题破解

方法1：基本不等式法.

解析：取BC的中点D，连接AD.

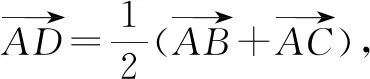
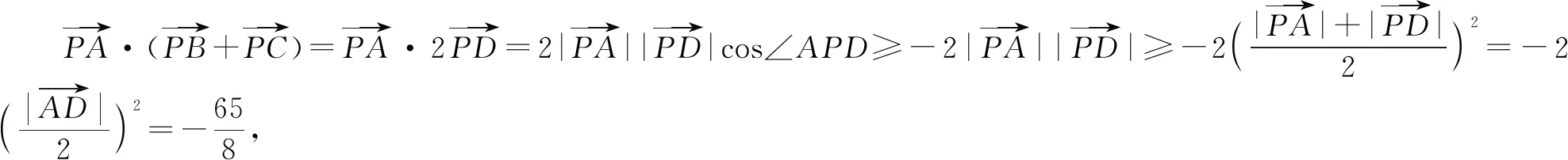
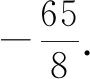
方法2：参数法.

解析：取BC的中点D，连接AD.

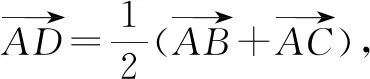
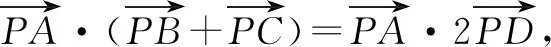
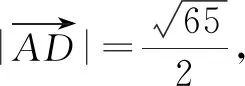
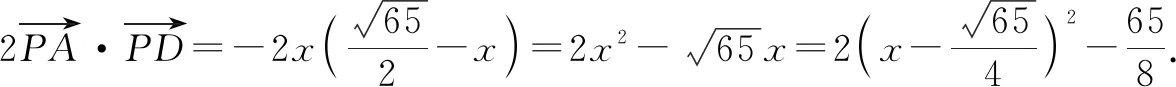
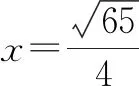
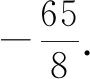
方法3：坐标法.

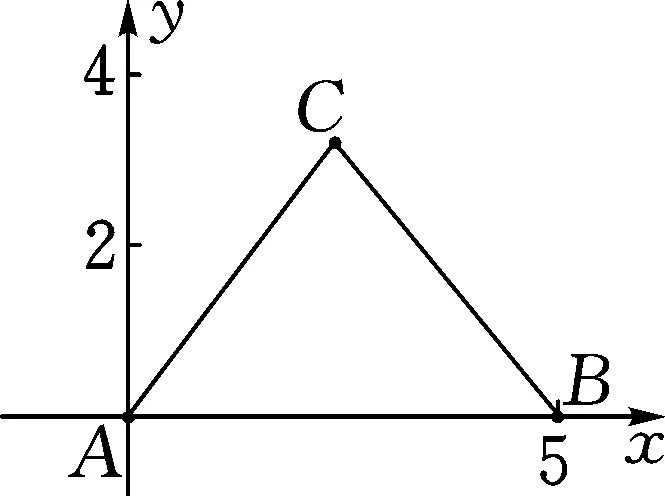
图1

解析：以点A为坐标原点，AB所在的直线为x轴建立平面直角坐标系，如图1所示.不失一般性，假定点C位于第一象限.

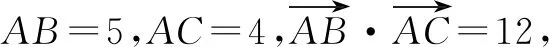
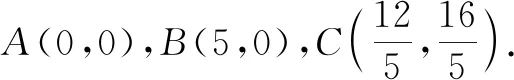
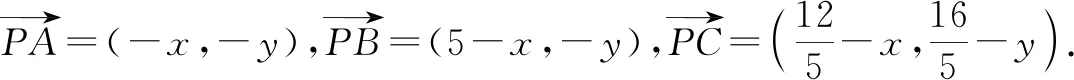
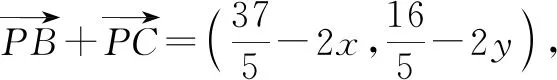
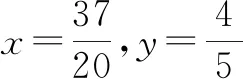
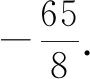
点评:以点A为坐标原点巧妙构造直角坐标系，结合题目条件确定点C的坐标，设出点P的坐标，利用平面向量的坐标运算与数量积公式得到涉及参数x，y的二次关系式，通过合理配方，结合函数思维来确定最值即可．坐标法可以借助平面直角坐标系的建立，以及坐标的代数运算来合理转化，化“形”为“数”，利用代数运算来达到目的．

方法4：极化恒等式法.

解析：取BC的中点D，连接AD.

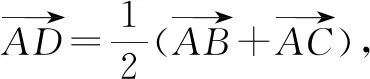
那么结合极化恒等式，可得

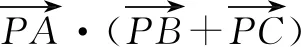
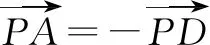
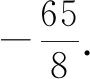
4 问题背景

以上赛题改编于2017年高考数学全国卷Ⅱ理科第12题，是在原来特殊三角形——等边三角形的基础上，加以一般化处理．

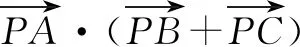
由于涉及特殊三角形——等边三角形，此高考真题破解起来更为简单快捷，可以参考以上赛题的破解方法加以分析与处理．(此题答案：B)

5 教学反思

5.1 方法归纳

在解决平面向量的数量积问题中，可以利用基底向量，借助平面向量的线性运算，结合基本不等式、极化恒等式等加以处理；也可以利用平面直角坐标系，借助平面向量的坐标运算，结合函数等加以处理；有时还可以直接利用图形特殊，结合平面向量的“形”的特征加以处理;等等.这些都是竞赛、高考中解决此类问题比较常见的一些技巧方法．

5.2 核心引领

在破解平面向量的最值问题时，问题切入的关键是根据题目条件，从平面向量的相关概念、相关运算、相关图形的本质出发，选取代数与几何、数与形等方式，以概念法、函数法、三角函数法、数形结合法以及不等式法等行之有效的基本方法来参与，借助平面向量的相关运算等来解决，进而有效达到解决相关最值问题的目的，融合数学知识，提升解题能力，拓展数学思维，培养核心素养．Z