船体静水及波浪航行时在STAR-CCM+软件中仿真结果的有效性验证

张大朋，赵博文，严 谨，侯 玲

(1.广东海洋大学 海洋工程学院，湛江 524005；2.浙江大学 海洋学院，舟山 316021)

近年来，由于高速计算机的迅速发展和普及，采用数值模拟预报船舶航行性能受到众多研究者的青睐。数值方法能够模拟船体周围的流场流动，得出阻力数值和流场的流动细节[1]。此方法省时省力，能够进行实尺度模拟，对于船舶快速性的研究起着重要作用。早期的数值模拟通常基于势流理论，即忽略流体粘性。此方法相对简单，计算量较小，被广泛应用于预报船体运动响应和粗估总阻力。然而，近年来，大量的船模试验结果表明，流体粘性、砰击、甲板上浪等因素对于船体运动和力的响应不可忽略，且会产生比较明显的非线性现象。基于势流理论的数值计算难以模拟这些强非线性因素。基于此，人们开始将目光投向能够充分考虑流体粘性作用的CFD(Computational Fluid Dynamics)方法[2-3]。CFD方法具有预报精度高、适用性广、成本低廉、周期短等优势。此外，CFD方法还具备一些特殊的优势，比如可以实现一些在试验中难以实现的条件；根据数值计算结果对流场细节展开分析(如压力、流线、速度矢量)，来揭示船舶水动力问题的机理等。CFD方法正在逐渐成为研究船舶在粘性流场中水动力学问题的重要而有效的手段[4-6]。

常用的CFD仿真软件有OpenFOAM、FLUNET以及STAR-CCM+等[7-10]。由于开发的时间较早，OpenFOAM以及FLUENT的应用已经比较成熟，这两种软件计算结果的准确性已经得到了广泛验证[11-12]。作为近几年刚开发出来的一种CFD仿真软件，STAR-CCM+的准确性还有待进一步验证。为验证STAR-CCM+软件计算的正确性，选取经典的行业内CFD考核验证的标准船型之一KCS(KRISO Container Ship)船模作为建模对象，计算了该船模的相关性能，并将计算结果与前人的试验结果进行了对比。经过对比发现，运用该软件计算船体在静水中航行时的水动力性能是比较可靠的。

1 KCS船模的几何参数及建模

KCS是一艘由韩国KRISO(Koera Research Institute of Ship and Ocean Engineering)设计的现代集装箱船型，在Gothenburg2000会议中被列为CFD考核验证的标准船型之一[13-15]。KCS船模有一个较大的球鼻艏和复杂的尾部曲面，属于肥大型船。本文KCS模型由澳大利亚Formation Design Systems公司自主研发的船舶专用软件MAXSURF构建，几何模型如图1，主尺度列于表1中。计算工况选用设计航速2.196 m/s(弗劳德数Fr=0.26)。

图1 KCS计算模型Fig.1 Computation model of KCS1.1 KCS船模的几何参数

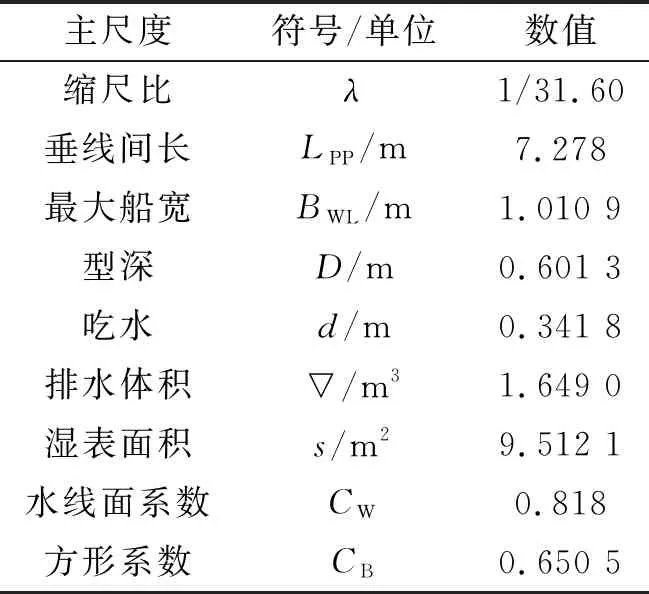
表1 KCS主要参数Tab.1 Main parameters of KCS

1.2 计算模型的建立

对于拖曳试验池，围绕船体创建一个体形状的几何，然后从体中减去船体，生成的体积为包含船体外形的连续且封闭的虚拟拖曳试验池。由于船体模型关于中纵剖面对称，阻力只计算一边即可，如此可以节省计算资源和时间。对于常规低速船型，计算域的大小一般通过以下准则确定：入口边界距离船艏1倍船长，出口边界距离船尾2倍船长，船上方1倍船长，船下方2倍船长。

由于KCS的船艏和船尾曲率变化较大，因此在划分网格的过程中，需要对其周围区域进行加密，此外，为了提高流体特征的分辨率，更好地捕捉流动分离现象和凯尔文尾流，也对相应区域进行了体网格加密。对于此类船舶两相流的模拟，加密自由液面区域(即水和空气的交界面)也尤为重要。

有鉴于以上原则，计算域的范围为：入口边界距船艏约1.5LPP，出口边界距船尾约2.5LPP；上边界距船模甲板1.5LPP，下边界距底板约3LPP；侧边界距船模左舷侧1.5LPP。计算网格采用STAR-CCM+自带的切割体网格生成器生成。用于网格收敛性验证的网格数量分别为：2.0×106、2.5×106、3.0×106，网格增长率为1.2。为了更好地捕捉流场，自由液面和船艏船尾处网格加密。湍流模型采用Realizablek-ε模型。时间步长0.04 s，内部最大迭代次数为10，计算过程中放开KCS船模纵摇和垂荡两个自由度，其余自由度固定。计算域与计算网格如图2和图3所示。

2-a 对称面 2-b 顶部面图2 计算区域与边界条件

3-a 全局网格 3-b 船艏处网格 3-c 船尾处网格图3 计算网格

图4 KCS运动坐标系Fig.4 Motion coordinate system of KCS

由于考虑了纵摇和垂荡两个船体自由度，除了空间固定坐标系外，本文还将引入一个新的运动坐标系。该运动坐标系是以船舶重心位置为原点、固定于船体上的空间三维直角坐标系，能够随船体摇荡，如图4所示。GX轴在中线面内，平行于基平面，指向船艏为正；GY轴垂直于中线面，指向左舷为正；GZ轴垂直于基平面铅直向上。GX、GY和GZ轴可近似认为是船体的三根惯性主轴。

网格收敛性的验证对象是无因次化的总阻力系数CT，定义如下

(1)

式中：RT为船受到的总阻力，N；ρ为水的密度，取20℃时海水密度1 025 kg/m3；v为船的航行速度，m/s；s为船体的湿表面积，m2。

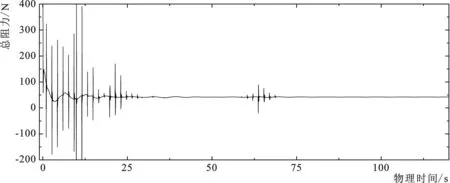
图5 密网格的半船阻力时历曲线Fig.5 Half ship resistance time history curve of fine grid

图5是密网格的半船阻力时历曲线。由图5可以看出，在物理时间小于25 s的计算前期，半船阻力曲线会出现较大的震荡现象，计算并不收敛，这和网格的质量与数量息息相关。此外，计算前期曲线还会出现较大的“脉冲”现象，这是由于船体不停地调整自由度所导致：船体每调整一次自由度，计算在该瞬时状态均会出现较大程度的发散，这就形成了所谓的“脉冲”现象。物理时间75 s后，半船阻力曲线逐渐收敛，“脉冲”现象也消失，说明计算逐渐达到稳定，最大物理时间120 s时的计算结果可以应用到实际工程上。

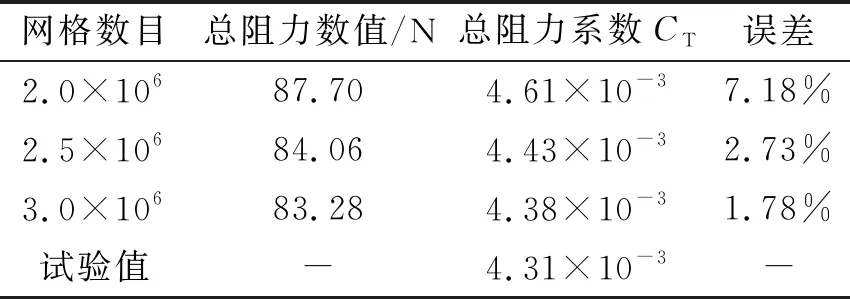
表2 计算结果Tab.2 Calculation results

网格收敛性验证结果显示在表2中。计算结果显示，三种数量的网格收敛效果均良好。三种程度的网格分别在物理时间43 s、37 s和33 s后达到准稳态求解，网格越密，阻力值达到收敛的时间越早。粗网格的计算有较大的误差，有将近7%的相对误差；中等网格和密网格的结果相近，误差均在2%以内。虽然与试验结果最相近的是密网格，误差仅有1.78%，但是网格数目增大所带来的计算负担和计算时间十分大，因此，在后续计算当中，均采用中等网格的配置，以减小计算负担。

本文采用的湍流模型为Realizablek-ε模型，SSTk-ω湍流模型下的KCS船模总阻力系数为4.43×10-3，与Realizablek-ε模型差距不大，说明湍流模型对本次计算的影响不大。因此在后续计算中将继续采用Realizablek-ε湍流模型。

2 仿真结果分析

为了充分验证该数值计算方法的可靠性，除了设计航速Fr=0.26外，本文还依照Gothenburg 2010研讨会中的算例，在中低速范围内选取了5个计算工况，均考虑船体自由度(升沉和纵倾)。本节将展示KCS船模在中低速范围内的总阻力系数变化，以及设计航速Fr=0.26下的船体表面压力分布、兴波状况、纵倾和升沉状况等，并作简要分析。

2.1 KCS船模在中低速范围内的总阻力系数

图6是不同航速下KCS的总阻力系数计算结果。从变化趋势上来看，KCS船模的总阻力系数CT先随着航速的增加而减小，达到Fr=0.195的工况后又快速上升。同试验值相比，本算例中的阻力计算结果较为准确。6个计算工况中，最大的误差发生在Fr=0.108处，为2.29%，这是由于低航速时阻力收敛较为困难导致。航速较高时仿真计算结果同试验值较为贴合。

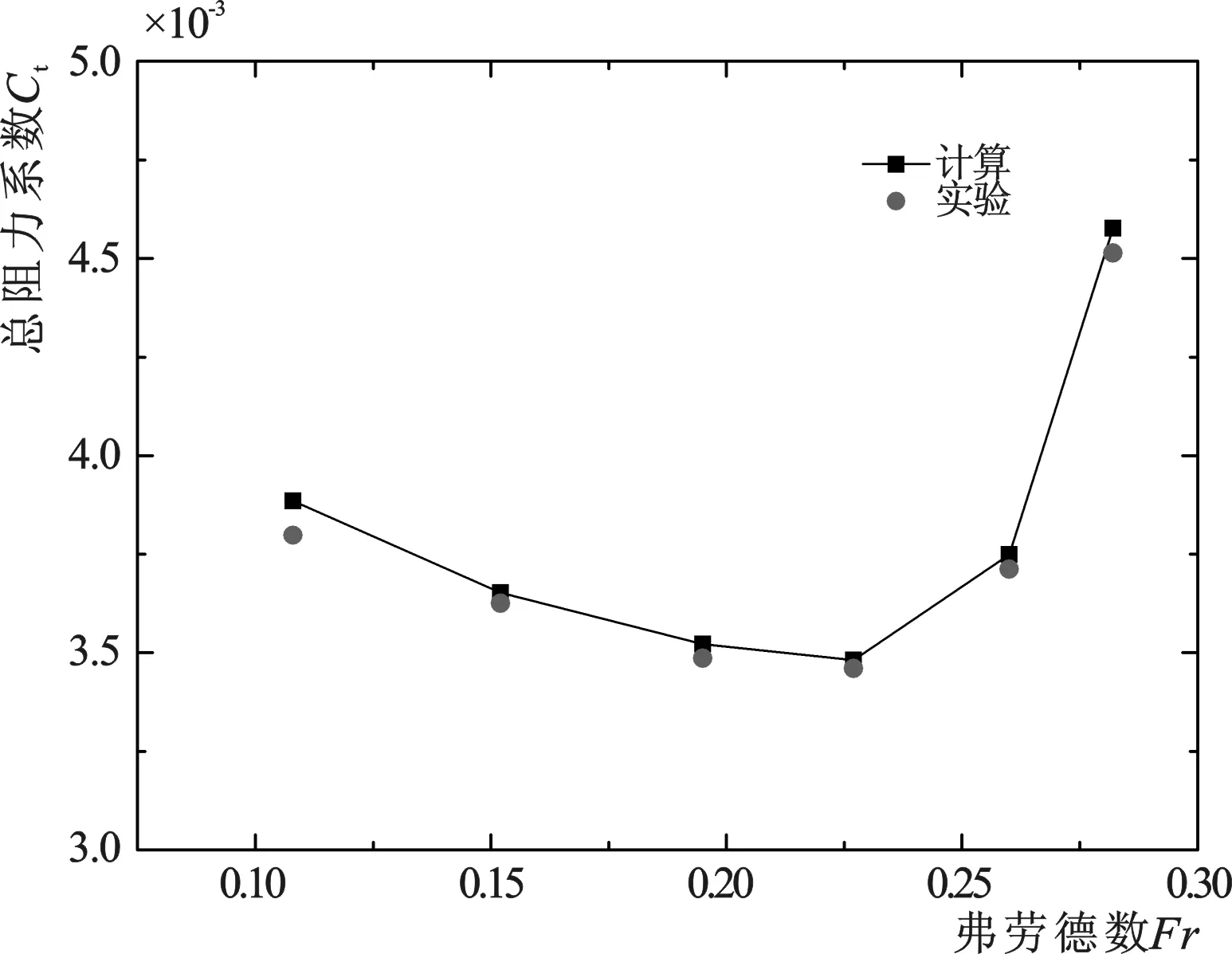
图6 总阻力系数比较Fig.6 Comparison of total resistance coefficient

2.2 KCS船模的船体表面压力分布

KCS船模在设计航速Fr=0.26下的船体表面压力分布如图7所示。由图7可知，船体的船艏劈水前行，导致艏部的压力峰值主要集中在球鼻艏最前端，球鼻艏中部存在一个低压区，说明球鼻艏能够对低速航行状态下的船舶起到一定的降压效果，而船体尾部的压力分布则比较平均。

7-a 船艏处压力分布 7-b 船尾处压力分布

7-c 全船压力分布

2.3 KCS船模的空间运动姿态

计算得到的KCS船模在不同航速下的升沉和纵倾结果与试验值的比较由图8所示。预报的升沉值和纵倾值与试验结果总体相近。从变化趋势上来看，升沉值随着航速的增加而增加，并且增速随着航速的增加而增加。纵倾值先往负值(艏倾)方向递增，在Fr=0.26达到负向最大值，然后往正值方向变化。

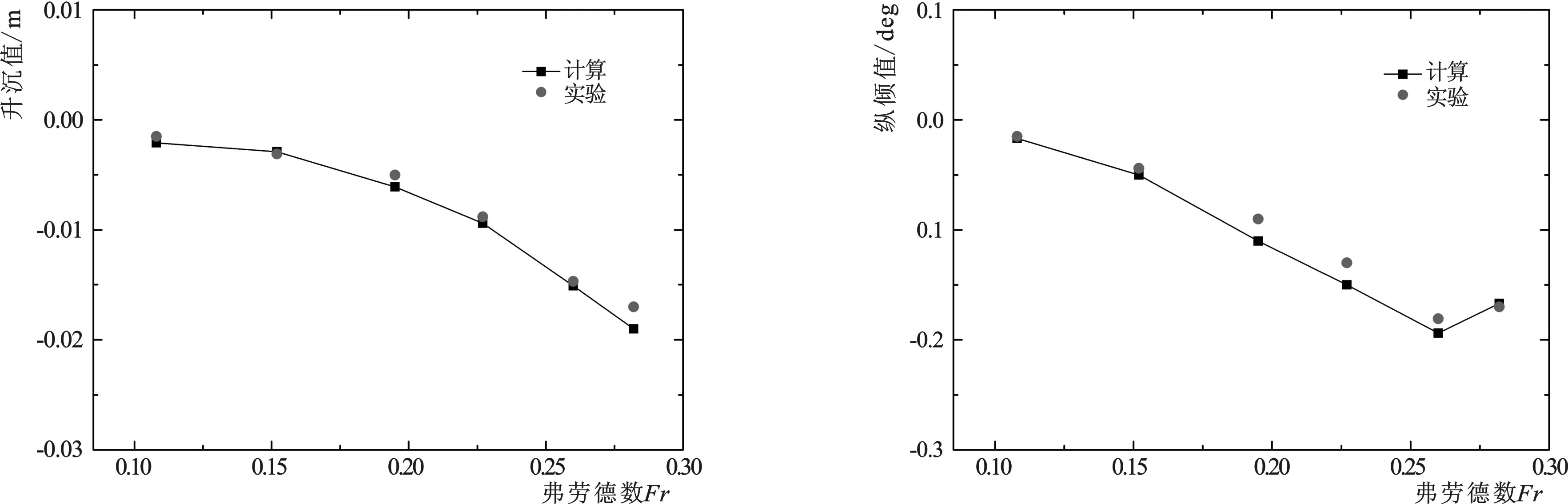
8-a 升沉 8-b 纵倾图8 升沉与纵倾比较

2.4 KCS船模在静水航行时导致自由液面的波形变化的仿真结果与试验结果的对比

当KCS船模以2.196 m/s的速度在静水中直航时，自由液面处的波形如图9所示。数值计算采用的VOF方法，对于肥大型船舶而言，可以精确地捕获凯尔文波。H/L是兴波高度与垂线间长的比值，该值越高表示船体兴起的波浪越高而且越陡。整个船波系基本上集中在凯尔文角所限定的扇形面范围之内，其中船艏和船尾处兴起的波浪最高。由于KCS船型加装了一个肥大的前伸型球鼻艏，该结构使得船体首部水线的坡度有明显减小，这导致船艏波的陡直程度有所下降，从而一定程度上减小了破波阻力，从图9中也可以看出船艏处的兴波高度略低于船尾。船艏波在船体表面最大波高处逐渐消失，波谷和波峰线的发散波分量会沿波浪区域边缘逐渐减小。船体进流段附近会产生一个明显的波谷，这将会增大船体的兴波阻力，对进流段处的型线结构进行优化可适当降低兴波阻力。目前，以船体阻力为目标函数的船体型线多学科设计优化仍是当下船舶CFD研究的热点方向之一，其中，进流段处的横剖面面积曲线便是重点优化对象。

当KCS静止时，方尾高出静水面，当KCS达到Fr=0.26设计航速时，其产生的波浪在方尾处上升。如果船的速度很高，在尾梁下面，波面将与船体表面平行。因此，方尾可能出现在水外区域，从而形成所谓的“干尾梁”。当船速很低时，波浪的产生可以忽略不计。然而，如果船舶以目前KCS情况下的中速前进，则在方尾上方上升的波浪和在横梁后面的逆流会形成不稳定且复杂的波形，从图9可以观察到横梁后方的波面看起来像不稳定的气泡。这种不稳定的复杂波形和流动状态会对螺旋桨和船舵产生不利的耦合作用。除此之外，若要在船尾处安装拖曳缆索或线列阵，其安装位置与长度也要综合考虑方尾处的兴波状况，避免复杂波形和流动状态给拖曳缆索带来不必要的疲劳损伤。对于此类型的船舶，船体去流段的波形较平缓，兴波高度较低，是安装缆索的较好位置。

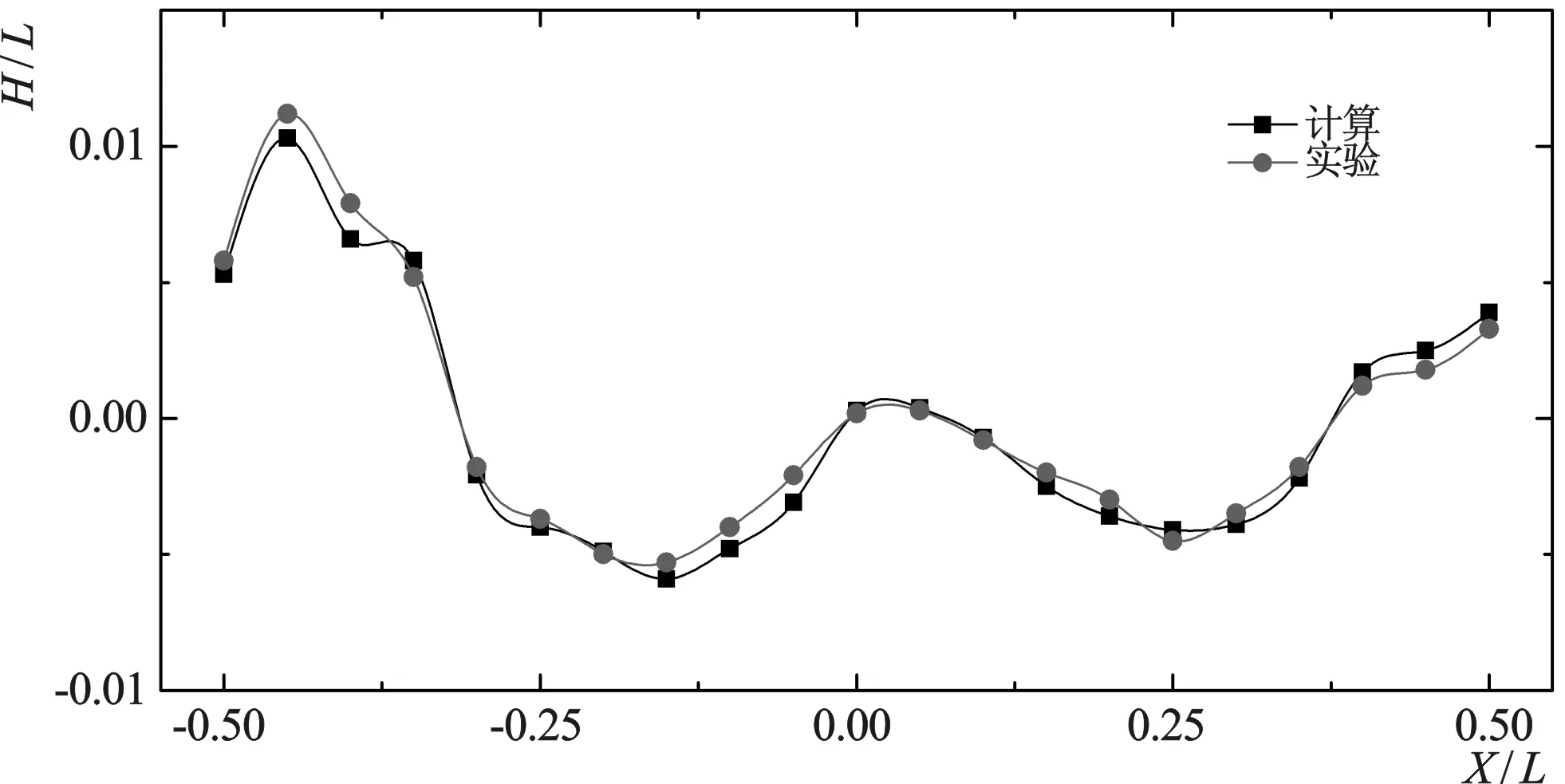
图10 船体表面波高Fig.10 Hull surface wave height

图10是仿真与试验船体表面波高的比较，与试验结果相比，计算得到的船体表面波高与试验测量值吻合较好。在Fr=0.26工况下，随着船速传播横波的相应长度为2πFr2，即0.425。船体表面预计有两个主要波长，波峰出现在X/L=-0.45和0.05处，波谷出现在X/L=-0.15和0.25处。第一个波峰超过了船长的1%，而第一个波谷为-0.5%。图中可以观察到，在第一个波峰之后的X/L=-0.4处存在来自前体的小波。船尾附近的波浪高度比船艏区域平坦得多。

2.5 KCS船模在波浪航行时的仿真结果与试验结果的对比

参考文献[16]的工作，KCS在波浪中的航行工况为：波高0.123 m、波长1.15LPP、航速Fr=0.26，波浪模型为一阶斯托克斯波。船模的运动通过重叠网格的运动来实现。由于船模在波浪中的运动和阻力具有一定的周期性，为便于比较和分析，需要对船体运动和受力进行Fourier变换。将得到的KCS船模在波浪中的阻力、升沉和纵摇随时间的变化进行Fourier变换，取Fourier级数的一阶量，与试验结果进行对比，列于表3中。

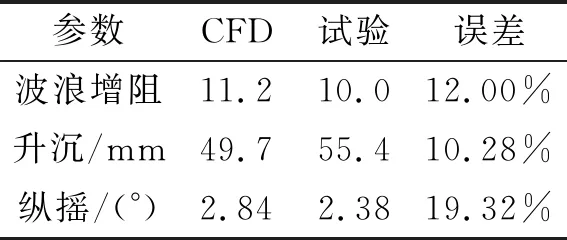
表3 波浪计算结果Tab.3 Calculation results of wave

由表3可知，波浪中阻力的计算值与试验值比较接近，但精度低于静水计算，尤其是船舶运动模拟的误差略大。原因在于，波浪中船模兴波与来波存在较强的相互干扰，计算中的非线性大幅度增加，且波浪中运动幅值高阶量，计算精度受到的挑战较大。但从整体上看，数值计算结果能比较好地反映出船舶的运动特点和受力大小。

图11是波浪流场中的典型时刻自由液面波形图。船舶在静水中以定常速率沿直线航行时存在两个波系：横波和散波，波系边界与船舶航向所夹的波浪半角为凯尔文角。当船舶在波浪中航行时，除了会产生与航行速度和水深相关的船行波外，还会产生另一种与入射波浪诱导船体运动相关的波。这两种波均会消耗船体的能量且互相叠加，因此船舶在波浪中航行时所消耗的能量要高于静水中，其中额外的能量损失即为所谓的波浪增阻。

11-a t=6.50 s 11-b t=6.75 s 11-c t=7.00 s 11-d t=7.25 s图11 波浪中典型时刻的波形

3 结论

运用STAR-CCM+进行船体的相关计算时，在建模阶段，模型的网格越密，阻力值达到收敛的时间越早，粗网格的计算会有较大的误差，加密网格可以有效提高计算精度，但是网格数目增大所带来的计算负担和计算时间却十分大，因此，在计算当中，建议用中等网格的配置，以减小计算负担，当且在仿真的初始阶段会出现较大的脉冲现象，这是船体在遭遇水流后调整自由度的结果。

运用STAR-CCM+软件计算的KCS船模在静水及波浪中直航所导致的波形与Kim等在2001年试验得到的波形高度吻合，从而了验证该软件数值的有效性以及良好的网格收敛性。