多锥构型摩擦副同步过程的影响因素分析

王延忠 窦德龙 张震 于祥云 孟祥文

(北京航空航天大学 机械工程及自动化学院，北京 100191)

湿式离合器广泛应用于车辆的自动变速传动系统，自诞生以来其结构形式未曾发生较大变化。传统多片式湿式离合器依靠轴向增加摩擦副对数来提高转矩容量以应对越来越苛刻的工况，如高能容和大冲击。然而，当前传动系统在朝着小体积和轻质量的方向发展，多片式湿式离合器为提高转矩容量而增加摩擦副对数，会直接导致车辆变速器的轴向尺寸变大。

多锥构型摩擦副是一种通过改变几何特征来提高摩擦副转矩传递能力的摩擦传动部件。不同于多片式湿式离合器在轴向增加摩擦副对数以提高转矩容量，多锥构型摩擦副以一种独特的结构，即沿径向同心排列多个不同几何参数的圆锥面来提高转矩传递能力。这种多锥宏观结构特征不仅提高了摩擦副的接触面积，而且每一组接触锥面都可看作一个楔形机构，起到自增力作用，能够以较小的轴向压紧力作用在锥面间产生较大的法向接触力，从而增大接触面间的摩擦力和摩擦转矩，实现小体积传递大转矩。

摩擦副接合传递转矩是一个动态过程，目前国内外研究人员主要通过仿真和试验手段来开展摩擦副动态接合过程的研究。Patir等[1- 2]提出了著名的Patir-Cheng平均流量模型，表征了三维粗糙表面对弹性流体动压润滑的影响，并利用平均流量模型建立了考虑压力流与剪切流因素、并以粗糙度特征为函数的平均雷诺方程。Natsumeda等[3]考虑纸基摩擦材料的渗透性、压缩应变和粗糙面接触，采用Patir-Cheng平均流量模型来分析油膜的挤压运动。 Berger等[4]利用所建立的有限元模型研究了施加的载荷、摩擦材料的渗透性和凹槽尺寸等对湿式离合器接合特性的影响。为了求解方便，Berger等[5]还将摩擦副等效为轴对称模型，从而简化了接合过程的数学模型。Gao等[6- 7]研究了表面粗糙度、流体黏度、材料渗透率、惯量、沟槽面积比和杨氏模量等参数对接合特性的影响规律。Razzzaque等[8]计算并分析了凹槽的几何形状、方向和施加的载荷对油膜厚度、传递扭矩、转速、挤压时间和黏性功率耗散等摩擦副接合过程物理量的影响。张志刚等[9]应用平均雷诺方程和粗糙表面弹性接触模型对湿式离合器的接合过程进行建模，研究了离合器的动态接合特性，并通过试验验证了模型的正确性和有效性。马彪等[10]基于改进的平均流量模型和Greenwood-Tripp接触模型建立了单摩擦副承载力方程和转矩方程,研究了离合器接合过程关键指标的变化规律。王成等[11]对湿式离合器的接合特性进行了仿真与分析。唐长亮等[12]针对湿式离合器的接合过程，设计并搭建了多模式加载试验台，对不同转速和控制油压下湿式离合器的接合特性开展了试验研究。于亮等[13]研究了润滑油黏度随温度变化后对铜基湿式离合器摩擦转矩的影响。杨辰龙等[14]对含沟槽湿式离合器的接合特性开展了数值与试验研究。以上的建模过程和试验研究均是针对传统多片式湿式离合器的平面摩擦副进行的。对于新型的多锥构型摩擦副，尚未见有学者对其动态接合特性开展系统研究。由于多锥构型摩擦副的宏观界面特征发生了颠覆性变化，故文中对多锥构型摩擦副的接合过程进行数学建模，分析结构参数对摩擦副接合过程的影响。

文中针对多锥构型摩擦副的几何特征，从简化的单锥结构出发，基于润滑力学理论和微凸体接触理论，建立油膜挤压模型、微凸峰接触模型、承载力模型和传递转矩模型，并将其进一步拓展到多锥面组合的多锥结构，应用四阶龙格库塔数值法进行求解，得到油膜厚度、传递转矩等随接合时间变化的结果，并进一步分析了各操作参数和摩擦副构型参数对接合过程的影响规律。

1 结构表征与数学建模

1.1 结构组成与参数化表征

多锥构型摩擦副的实物及模型简图如图1所示，由处于中间位置的摩擦元件和其两侧的对偶元件，以及起到脱开摩擦副作用的回位弹簧构成，摩擦元件与传动轴通过花键连接，既可随轴转动又可沿轴向运动，其中一个对偶元件靠近液压缸一侧，与离合器毂通过花键连接且只可做轴向运动。

为了便于程序编制，将多锥构型摩擦元件进行参数化表征。假设多锥构型离合器每侧摩擦副各有N(N=2n-1)个圆锥接触面，从内径到外径依次为每个圆锥接触面编号为2k-1(k=1,2,3,…,n)。摩擦锥面半锥角为α(即圆锥面与轴向的夹角)，圆锥顶部宽度为W，两相邻圆锥顶部间距为V，接触锥高为L，锥面径向排列的周期间距为δ，摩擦元件内径为R0，第一锥面近轴心端半径为Ri1，远轴心端半径为Ro1。根据几何关系，可得接触区长度b和锥面径向排列周期间距δ的表达式如下：

b=(V-W)/(2sinα)

(1)

δ=V+W

(2)

不考虑实际结构的制造误差和油槽结构，假设离合器两侧摩擦副的结构对称，文中只分析一侧摩擦副的接合过程，如摩擦元件与对偶元件1组成的摩擦副。由几何关系，可得编号为奇数2k-1的圆锥接触面母线的近轴心端半径为

Ri_2k-1=Ri1+(k-1)δ

(3)

远轴心端半径为

Ro_2k-1=Ri_2k-1+bsinα

(4)

同理，编号为偶数2k的圆锥接触面母线的近轴心端半径为

Ri2k=Ri1+(k-1)δ+bsinα+W

(5)

远轴心端半径为

Ro_2k=Ri_2k+bsinα

(6)

1.2 接合过程的分析模型

1.2.1 油膜挤压模型

根据多锥摩擦元件的构型特点，将其等效成多个独立的锥面摩擦副，又因整个摩擦副在圆周上可看作轴对称模型，对于任意圆锥接触面，不考虑润滑油受到的离心作用及其在锥面上的相对速度滑移，结合Patir-Cheng平均流量模型，引入压力流量因子对油膜压力进行修正，如图2所示，将摩擦副接合过程的润滑力学模型简化为一维修正雷诺方程

(7)

式中，φx为x方向的压力流因子，p为油膜压力，η为润滑油黏度，hT为油膜厚度，t为时间。

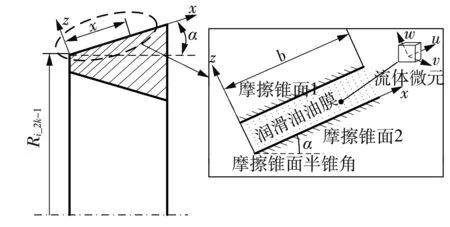
图2 锥面油膜挤压模型Fig.2 Oil film extrusion model on cone

根据文献[1- 2]，φx可表示如下：

φx=1-0.9e-0.56H

(8)

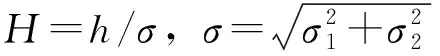
假设圆锥面接触边界处的流体压力为零，则油膜压力边界条件如下：

p(x=0)=p(x=b)=0

(9)

对式(7)积分两次并代入边界条件(9)，得到润滑油油膜在x方向上的压力分布：

(10)

根据链式求导法则，油膜厚度hT对时间t的求导可转换成摩擦副平均间隙h对时间t的求导，即

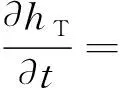
(11)

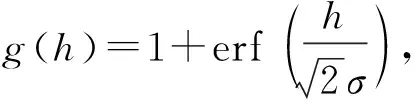
(12)

1.2.2 微凸峰接触模型

根据文献[3]，考虑粗糙接触的平均压力pc，将其设置为与当量弹性模量E成比例，同时与实际接触面积Ac和名义接触面积An之比成正比，即

(13)

实际接触面积Ac利用文献[15]中的经典粗糙表面接触模型确定，则有

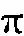
(14)

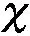
(15)

式中，z为微凸峰高度。

1.2.3 承载力模型

混合润滑阶段，名义接触面积内同时分布着润滑油膜和微凸体，当湿式摩擦副接合时，润滑油流体动压效应产生的油膜承载力Fh与粗糙表面微凸峰承载力Fc共同承担轴向加载力Fapp，其中微凸峰承载力Fc可通过粗糙表面接触模型计算，油膜承载力Fh可通过对油膜压力分布积分得到。考虑锥角效应，则

(16)

(17)

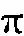
(18)

式中:S为摩擦副间的接触面积;p0为加载压力;Ra和Rb分别为对偶元件背面受加载压力作用的外径和内径;υs表示加载压力的上升速度，为无量纲量，文中取值为10。

1.2.4 传递转矩模型

湿式离合器摩擦副在动态接合过程中，其主动片带动从动片转动，直至二者的相对角速度减小至零，主、从动片之间传递的转矩T由油膜黏性剪切转矩和粗糙表面微凸体接触形成的摩擦转矩共同组成，可建立如下转矩平衡方程：

T=Th+Tc

(19)

式中,Th为黏性剪切转矩，Tc为摩擦转矩，其中

(20)

式中，φf和φfs为Patic-Cheng剪切流量因子，r为摩擦副中任一点到中心轴线的径向距离，ωrel为摩擦元件与对偶元件之间的相对转速。

(21)

式中，滑动摩擦系数fc是相对滑动速度ν的函数[16]，

fc=0.13+0.008logν

(22)

如果同时考虑多个锥面摩擦副，则名义接触面积为

(23)

油膜总承载力Fh_all与微凸峰总承载力Fc_all的表达式如下：

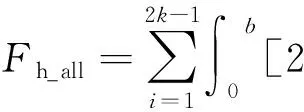
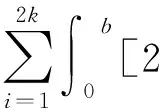
(24)

(25)

油膜总黏性剪切转矩Th_all与微凸峰总摩擦转矩Tc_all的表达式如下：

(26)

(27)

湿式摩擦副的从动片与负载端连接，在主动片对从动片的转矩作用下，从动片连同负载端开始转动。设从动片及负载的等效转动惯量为I，ω2为从动片角速度，则

(28)

2 同步转矩的计算

根据上述系列公式推导出的油膜厚度变化率公式和角速度变化率公式为常微分方程，可采用经典四阶龙格库塔法对二者的联立方程进行积分求解，时间步长取Δt=0.001 s，迭代结束条件为主从动片相对转速为零，仿真参数如表1所示，计算流程如图3所示。

表1 数值仿真输入参数Table 1 Input parameters of numerical simulation

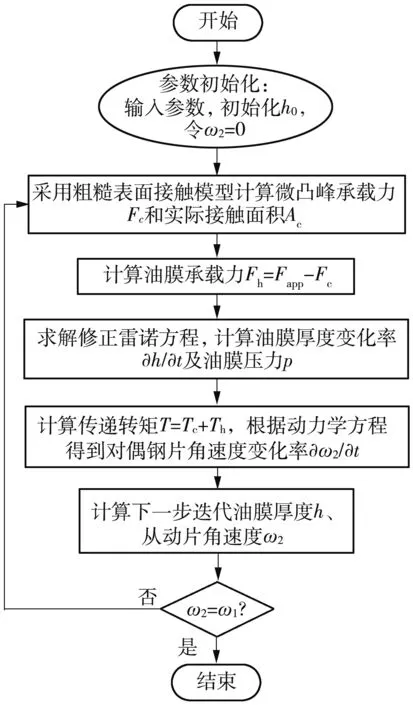
图3 同步模型计算流程Fig.3 Calculation process of synchronous model

3 同步过程影响因素分析

从宏/微观界面特征和工况操作参数出发，分析各因素对多锥构型摩擦副动态接合过程主要性能指标的影响，其中宏观界面特征主要包含多锥构型摩擦元件的锥面造型及尺寸，如锥角、摩擦锥面数量等；微观界面特征主要是指表面粗糙度。工况操作参数主要包含主从动片初始相对转速和加载压力。

3.1 锥角的影响

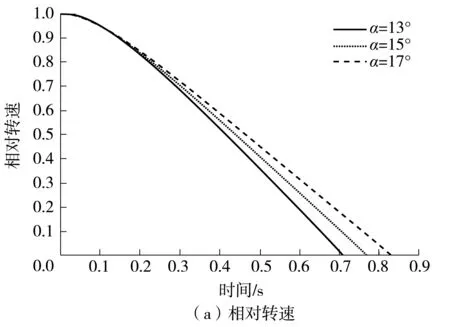
锥角是多锥构型摩擦副的典型特征参数，改变锥角可改变摩擦副的受力状态。锥面接触构成楔形机构，使锥面之间的法向接触力大于轴向加载压力，起到自增力效果。为探明锥角对多锥构型摩擦副接合过程的影响，分别对不同大小锥角(α=13°,15°,17°)的多锥构型摩擦副接合过程进行仿真分析，其他参数保持与表1中一致。

由图4可知:在所研究的锥角范围内，随着锥角的增大，同步时间逐渐延长，油膜厚度变化速率有所增加但不是十分明显；锥面法向微凸峰承载力和间隙油膜承载力显著降低，但二者随同步时间变化的趋势并未发生改变。同时可以发现，锥面法向微凸峰承载力远远大于轴向加载压力，即具有自增力效果。锥角为13°时锥面法向最大微凸峰承载力发生在同步结束时，达15.46 kN，锥角为15°时达13.61 kN，锥角为17°时达12.11 kN。油膜承载力最大值发生在开始接合的前0.1 s内，分别为3.480、2.541和1.953 kN。由于在同步阶段粗糙摩擦转矩占主导地位，因此不同锥角同步转矩的大小关系与锥面法向微凸峰承载力的大小关系一致，即锥角越小，同步转矩越大，同步时间越短。适当减小锥角有利于增大同步转矩，缩短同步时间，但锥角不易过小，否则易导致摩擦副自锁，不能正常脱离。

3.2 摩擦锥面数量的影响

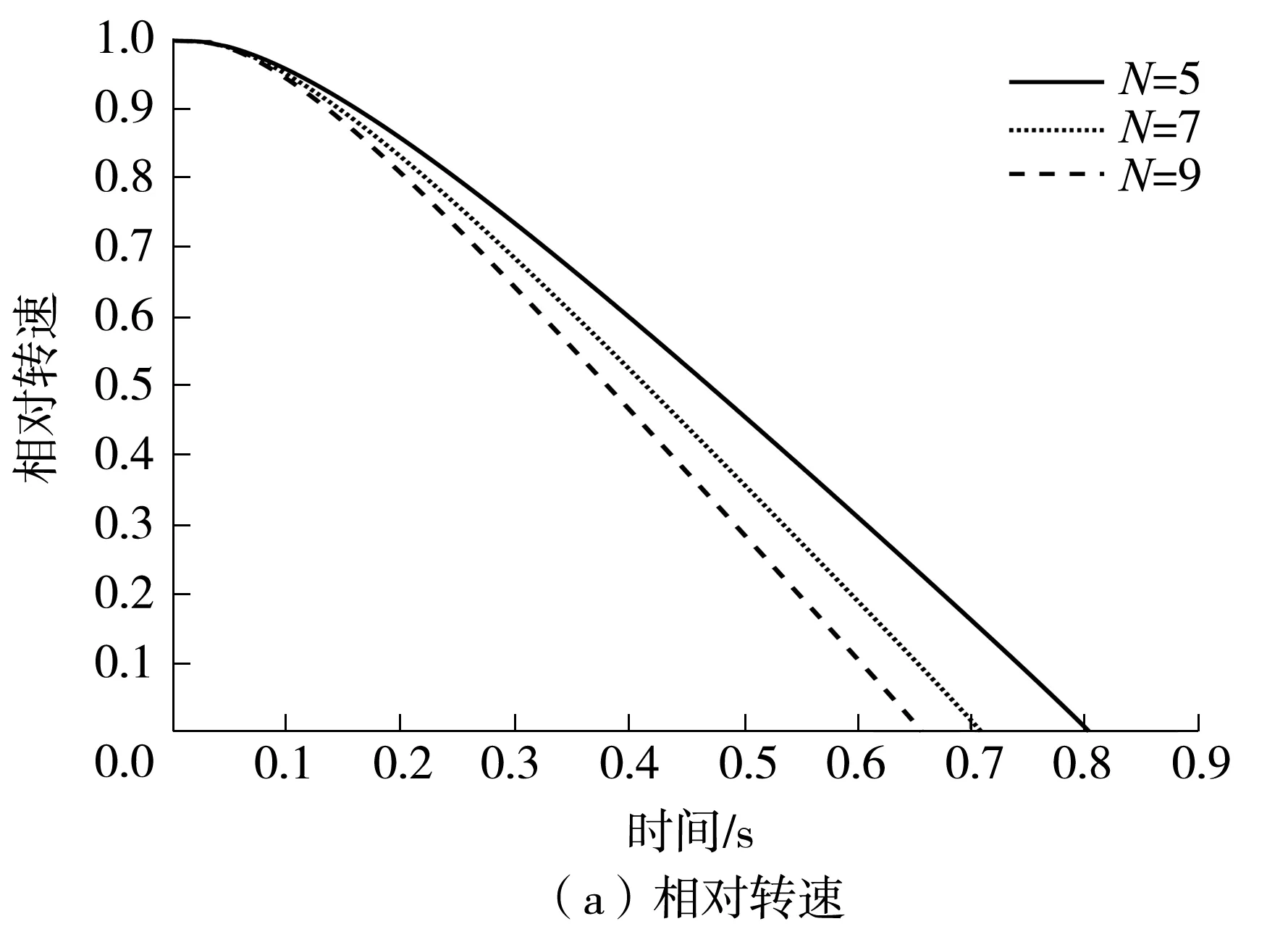
多锥构型摩擦副可以通过增加摩擦锥面数量来提高转矩传递能力，相应地也会增加摩擦元件的径向尺寸。为探明摩擦锥面数量对同步过程的影响规律，分别对不同锥面数量(N=5,7,9)的多锥构型摩擦副接合过程进行仿真，其他参数保持与表1中一致。

由图5可以明显地观察到摩擦锥面数量对同步过程的影响——在相同的轴向加载力下，增加锥面数量会直接增大摩擦接触面积，摩擦转矩峰值、黏性剪切转矩峰值增大，同步时间缩短，同步结束时最小油膜厚度逐渐增大。锥面数量为5、7、9时对应的同步时间分别为0.805、0.710、0.658 s。图5(c)中所示的微凸峰承载力和油膜承载力为所有锥面上的总和，随着锥面数量的增加，总的微凸峰承载力增大更为显著，油膜承载力峰值变化不明显，但是峰值过后油膜承载力随着接触面积的增大而逐渐减小。

3.3 表面粗糙度的影响

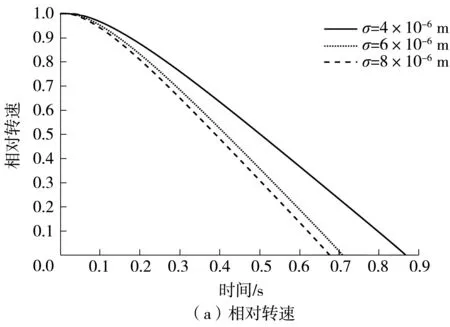
从湿式摩擦副接合模型可知，粗糙度的影响主要通过粗糙表面接触模型实现，对不同表面粗糙度(σ=4×10-6,6×10-6,8×10-6m)的多锥构型摩擦副接合过程进行仿真分析，其他参数保持与表1中一致。

如图6所示，摩擦表面粗糙度越低，接合过程中摩擦副间的最小油膜厚度越小，即摩擦副间的平均间隙越小。随着表面粗糙度的增大，更多表面微凸峰参与接触，微凸峰承载力增大，摩擦转矩增大，导致润滑油流体动压效应所产生的油膜承载力减小，润滑油黏性剪切转矩相应减小。从图6(c)可看出，表面粗糙度的增大使粗糙微凸峰接触的响应时间提前，从而使摩擦转矩更早地参与转矩传递，缩短了同步时间。同时，油膜承载力峰值出现的时间提前，在σ分别为4×10-6、6×10-6和8×10-6m时，油膜承载力峰值和相应的出现时间分别为(6 729 N，0.156 s)、(3 438 N，0.037 s)和(2 225 N，0.020 s)，其原因是粗糙度的变化主要影响微凸峰承载力，进而影响油膜承载力峰值，并未改变油膜承载力的变化速率，故在油膜承载力上升阶段，峰值越大，其发生的时间越滞后。

3.4 主从动片初始相对转速的影响

不同主从动片初始相对转速(n0=1 000,1 250,1 500 r/min)对多锥构型摩擦副接合特性的影响如图7所示。可以看出，主从动片初始相对转速对油膜厚度几乎没有影响，由于不考虑润滑油的离心作用，因此相对转速对微凸峰承载力和油膜承载力的影响也可忽略不计。文中假设从动片初始转速为零，则初始相对转速其实就是主动片的初始转速，随着初始相对转速增大，油膜剪切转矩有一定程度的增大，从而使粗糙表面摩擦转矩在总转矩中的比例有所减小。但是总体而言，同步时间增加得更为显著，在初始相对转速分别为1 000、1 250、1 500 r/min时，同步时间分别为0.529、0.621、0.710，由3组数据中相对转速增量与时间增量的比值可以发现，相对转速的变化与时间大致呈线性关系，可以认为在其他参数一定的情况下，同步时间与主动片初始相对转速大致成正比关系。

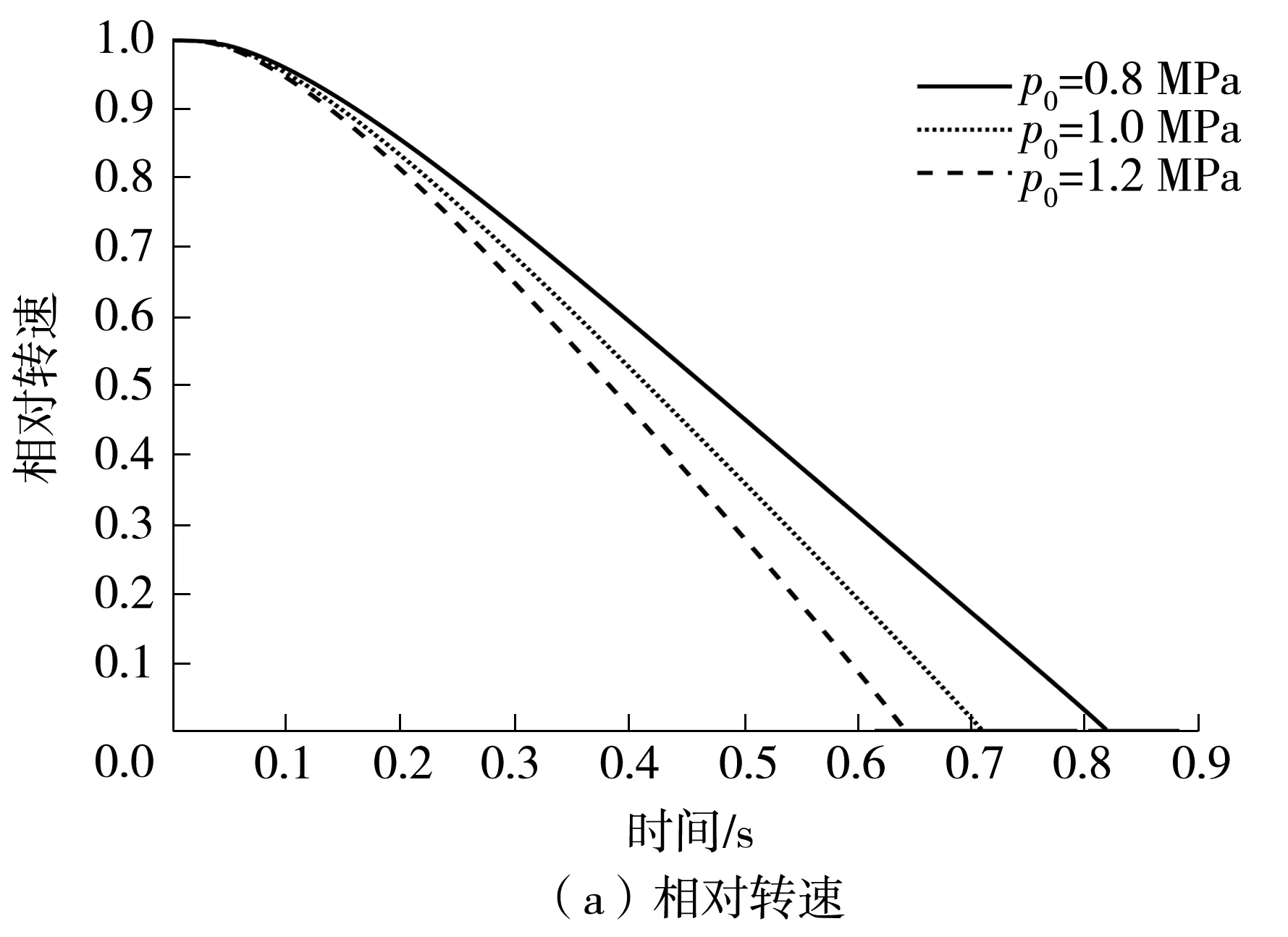
3.5 加载压力的影响

如图8所示，当加载压力增大时，粗糙表面微凸峰承载力和润滑油油膜承载力均增大，摩擦副平均间隙减小，最小油膜厚度减小。在相同的粗糙表面摩擦系数下，粗糙表面摩擦转矩增大，摩擦副传递的总转矩增大，同步时间因而缩短。加载压力p0分别为0.8、1.0和1.2 MPa时所对应的同步时间分别为0.819、0.710和0.642 s。进一步地，由图8(c)可以看出，在不同加载压力下，油膜承载力峰值拐点的时间基本一致，故加载压力对同步过程由挤压阶段过渡到边界润滑阶段的时间几乎没有影响，其影响的只是峰值大小。

4 结论

1)锥角对润滑油油膜厚度影响较小，对锥面法向微凸峰承载力影响较大，具有明显的自增力效应，适当减小锥角可有效提高摩擦副的转矩传递能力，但应避免锥角过小导致自锁现象的发生。

2)在一定轴向加载力作用下，摩擦锥面数量越大，同步转矩越大，同步时间越短，但并非呈线性规律变化。实际上，锥面数量过大会造成局部锥面润滑不良和过大的制造误差，反而影响多锥构型摩擦副的同步性能。

3)表面粗糙度会显著影响最小油膜厚度，表面粗糙度越低，摩擦副平均间隙越小，最小油膜厚度越小。表面粗糙度增大，微凸峰承载力增大，粗糙表面摩擦转矩增大，润滑油油膜承载力相应减小，润滑油黏性剪切转矩减小。特别地，微凸峰接触的响应时间提前，有助于缩短同步时间。

4)在其他工况参数和结构参数一定的情况下，主从动片初始相对转速主要影响同步时间，且二者大致呈线性关系，即初始相对转速越大，同步时间越长。

5)随着加载压力的增加，微凸峰承载力和油膜承载力的峰值显著提高，同步时间缩短，但加载压力对同步过程由挤压阶段过渡到边界润滑阶段的临界时间几乎没有影响。