控制子区内协调路径集的构成及优选方法

卢凯 吴蔚 邓兴栋 汪丽

(1.华南理工大学 土木与交通学院/亚热带建筑科学国家重点实验室，广东 广州 510640；2.东南大学 现代城市交通技术江苏高校协同创新中心，江苏 南京 211189；3.广州市城市规划勘测设计研究院 广东省城市感知与监测预警企业重点实验室，广东 广州 510060)

随着路网交通信号控制精细化管理要求的日益提高，区域协调控制的方向性需求也愈加明显，如何进一步细化交通信号控制的层次结构，使之能够满足各路段连线的不同协调控制需求，是现代交通控制所面临的一个基本问题。

传统的协调设计主要选取控制子区[1]或交叉口群[2]作为对象，其本质是研究交叉口的归属问题。不少国内外学者分别考虑路口间距[3- 4]、交通流量[3,5]、交通密度[6]、排队长度[7- 8]、信号周期[7- 8]、信号相位[9]、交通状态[10]以及饱和度[11]等因素对交叉口关联度进行分析，并以此作为控制子区与交叉口群划分的依据。现有研究多是利用单个或多个影响因素，通过建立关联度模型[7- 9]来综合评价交叉口之间的关联性强弱，控制子区与交叉口群的划分算法主要利用遗传算法[12]、模糊算法[13]、Newman算法[14]、Ncut算法[6]、k-均值聚类算法[15]、层次聚类法[16]。例如，卢凯等[12]提出了一种快速划分控制子区的方法，利用降维处理和遗传算法解决划分过程中出现的维数灾难问题；田秀娟等[14]通过对交叉口间关联性影响因素进行综合分析，利用改进的Newman算法实现了面向不同时段交通特性的控制子区动态划分；曲大义等[16]在传统关联度模型的基础上，考虑车辆的离散性、阻滞性及起讫点分布，建立了路径关联度模型与基于层次聚类法的交叉口群动态划分方法；段后利等[17]考虑车队行驶的离散性，建立了基于超图划分算法的控制子区划分模型，并通过实际路网分析了控制子区划分算法在高峰与平峰时段的适用性；别一鸣等[18]根据饱和度分析了不同状态下子区划分的目标与优先级问题，建立了关联度模型和子区划分算法，提出了控制子区划分框架及动态划分策略。

由于现有的协调设计对象优选方法多以交叉口之间的关联度大小作为参考依据，通过确定交叉口的归属特性来对控制子区或交叉口群进行划分，故而很少差异化对待控制区域内甚至交叉口之间的方向性协调控制需求，难以解决控制子区内协调路线之间的异质性问题，因此需要对控制子区与交叉口群进行再细化，充分结合路径上的交通需求及交叉口之间的可协调性，实现对区域交通协调设计对象的进一步优选。

文中提出细化控制子区(交叉口群)内的协调对象，通过建立协调路径、协调路径链、协调路径集这一组概念，实现对路网交通协调控制结构的分解与细化，并根据路径链所经过的交叉口数量(路径链长度)和所承载的交通流量，从路网中选取适当的协调路径链以构成协调路径集，使协调控制方案设计能够最大限度地考虑到子区内的行驶车流，实现信号协调控制对象的灵活选取，为区域协调控制结构的精细化提供技术支撑。

1 协调路径集的构成

1.1 协调路径集

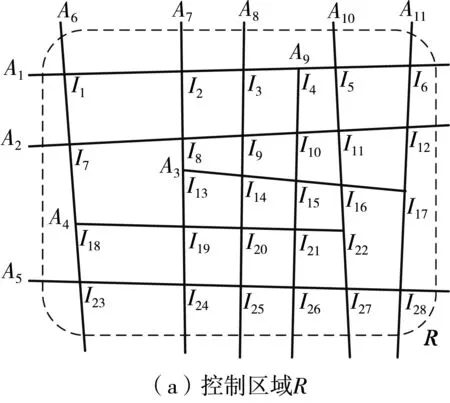
例如，如图1(a)所示，某控制区域R由11条道路A1、A2、……、A11相交而成，其中包含I1、I2、……、I28共28个交叉口，通过子区划分方法将其划分成3个控制子区G1、G2、G3，如图1(b)所示。

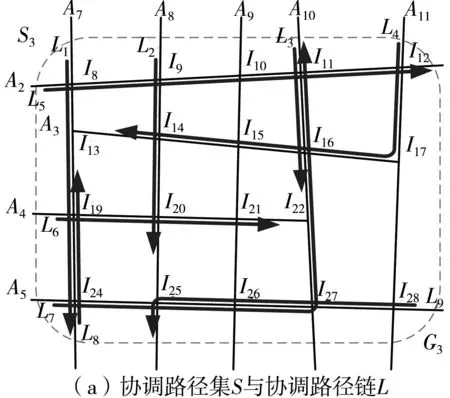
假定在控制子区G3中，行驶线路L1、L2、……、L9上的交通流量较大，协调控制需求较高，需选取它们作为协调对象，如图2所示。为此，定义协调路径、协调路径链、协调路径集的概念如下。

定义1协调路径协调路径是一条连接上下游交叉口相关进出口道的有向连线，它既反映了相邻交叉口之间的有向关联，也代表了需要进行协调设计的行驶车流。在同一条路段上，对于不同类型的行驶车流，例如公交车流与社会车流，如果它们的路段行驶特性或者路口控制相位存在差异，则需要将其定义为不同类型的协调路径。任意一条协调路径包含两个信号控制交叉口，通过信号交叉口节点实现与同类型上下游协调路径的连接。

定义2协调路径链协调路径链是一条由若干同一类型协调路径首尾相连构成的有向连线，它代表了一条需要进行协调设计的行驶路线。对于不同类型的协调路径，即使它们首尾相连，但由于上下游协调车流发生变化，因此也不能构成一条协调路径链，而需要作为两条协调路径链进行处理。两条协调路径链之间可以存在一个或多个交叉节点，通过在交叉节点设置相位时间基点约束条件，可以建立起协调路径链之间的交叉关系。

定义3协调路径集协调路径集是一个由若干条协调路径链构成的相交连线集合。协调路径集与控制子区包含同一个受控交叉口集合，即它们在交叉口归属特性上保持一致，但协调路径集还能够反映控制子区内所有需要进行协调设计的行驶路线，是对控制子区内所有协调控制需求的一种集中化描述。在协调路径集中，路径链数目越多、长度越长，则协调控制路段越多，但由于协调路径链之间的交点约束条件也将增多，部分线路协调控制效果可能下降。

为论述简便，在此不考虑车流类型对协调路径产生的影响，将协调路径命名为P(x,xa→xb;y,ya→yb)，其中x与y分别表示协调路径所经过的上游与下游交叉口编号，xa与xb分别表示协调路径穿过上游交叉口x的进口道与出口道编号，ya与yb分别表示协调路径穿过下游交叉口y的进口道与出口道编号；将协调路径链命名为L(x,xa→y,*→…→z,zb)，其中x、y、z表示协调路径链经过的交叉口编号，xa表示协调路径链进入第一个交叉口x的进口道编号，zb表示协调路径链离开最后一个交叉口z的出口道编号。

以图3所示的协调路径与协调路径链为例，协调路径P(1,4→2;2,4→2)表示选取从交叉口I1西进口至交叉口I2东出口的车流进行协调设计，其包含信号交叉口I1与I2；协调路径P(2,4→2;3,4→1)表示选取从交叉口I2西进口至交叉口I3北出口的车流进行协调设计，其包含信号交叉口I2与I3；通过交叉口节点I2将协调路径P(1,4→2;2,4→2)与P(2,4→2;3,4→1)相连，即可构成协调路径链L(1,4→2,*→3,1)，其表示选取从交叉口I1西进口至交叉口I3北出口的车流进行协调设计。协调路径链既可以由若干协调路径首尾相接而成，也可以仅由单条协调路径组成，如图3中的L(1,4→2,*→3,1)、L(2,2→1,4)、L(4,2→3,3)。

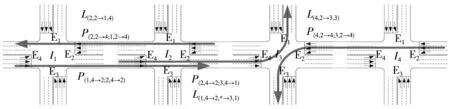
图3 协调路径与协调路径链的示例分析Fig.3 Example analysis of coordination paths and coordination path chains

图3中，由于协调路径链L(1,4→2,*→3,1)与L(4,2→3,3)存在1个交叉节点I3，因此交叉口I3的西进口左转相位时间基点O3WL与东进口左转相位时间基点O3EL将满足如下约束条件：

O3WL=O3EL+Δt3(EL→WL)+kC

(1)

式中：Δt3(EL→WL)为交叉口I3的西进口左转相位与东进口左转相位时间基点之间的时间间隔，其大小由交叉口I3的具体信号配时方案决定；C为信号周期；k为整数。

由于协调路径链L(1,4→2,*→3,1)与L(2,2→1,4)存在2个交叉节点I1与I2，因此交叉口I1、I2的西进口与东进口直行相位时间基点将满足如下约束条件：

(2)

由此可见，通过在交叉节点设置相应约束条件，可以实现协调路径链之间的共同优化。

图2中，协调路径集S3共包含9条协调路径链、12个交叉节点，其中由2条协调路径链相交形成的交叉节点共8个(I8、I9、I12、I14、I20、I25、I26、I27)，由3条协调路径链相交形成的交叉节点共4个(I11、I16、I19、I24)。对于1个由n条协调路径链相交形成的交叉节点，将确定n-1个相位时间基点约束条件，因此协调路径集S3总共将确定16个(8×1+4×2=16)相位时间基点约束条件。

协调路径集中协调路径链的交叉节点越多，则相位时间基点约束条件也越多，此时要获得理想的协调控制效果就越困难。若协调路径集中所有的协调路径链均不存在交叉节点，则所有交叉口都不存在相位时间基点约束条件，此时可以采取单向协调控制方式对控制区域内所有协调路径链进行信号控制。

由于相位时间基点约束条件是在协调路径集选取之后根据交叉口信号配时方案决定，因此文中不对其进行深入分析。

1.2 父路径与子路径

为了获得尽可能大的绿波协调控制效益，需要在考虑路径链交通流量与协调控制效果的条件下，最大限度地增加协调路径链的长度。为此定义父路径与子路径概念如下。

定义4父路径父路径是两条相连路径中的上游路径。

定义5子路径子路径是两条相连路径中的下游路径。

父路径与子路径是成对出现的。图3中，在协调路径链L(1,4→2,*→3,1)上，P(1,4→2;2,4→2)是P(2,4→2;3,4→1)的父路径，P(2,4→2;3,4→1)是P(1,4→2;2,4→2)的子路径。

再以图4所示的控制区域为例，对父路径、子路径以及协调路径链之间的关系分析如下：

①在协调路径链L(9,1→10,*→11,2)上，父路径为P(9,1→2;10,4→2)，子路径为P(10,4→2;11,4→2)，父路径与子路径在交叉口I10处通过共同的进出口方向E4→E2进行连接；

②父路径P(5,4→2;6,4→2)在下游交叉口I6的进出口方向E4→E2上产生4条子路径P(6,4→2;7,4→1)、P(6,4→2;7,4→2)、P(6,4→2;7,4→3)、P(6,4→2;7,4→4)，分别对应左转、直行、右转与掉头行驶方向，与之相应形成4条协调路径链L(5,4→6,*→7,1)、L(5,4→6,*→7,2)、L(5,4→6,*→7,3)、L(5,4→6,*→7,4)；

③在协调路径链L(5,4→6,*→7,1)的基础上，以P(6,4→2;7,4→1)作为父路径，在下游交叉口I7的进出口方向E4→E1上产生3条子路径P(7,4→1;3,3→4)、P(7,4→1;3,3→1)、P(7,4→1;3,3→2)，可延续分别形成3条协调路径链L(5,4→6,*→7,*→3,4)、L(5,4→6,*→7,*→3,1)、L(5,4→6,*→7,*→3,2)；

④路段掉头协调路径P(2,4→2;2,2→1)同样可以作为子路径与父路径P(1,4→2;2,4→2)相接，形成协调路径链L(1,4→2,*→2,1)。

由此可见，一条父路径可以衍生出多条子路径，因此在生成协调路径链时首先需要优选出延续父路径的子路径，即路径链的延伸方向。

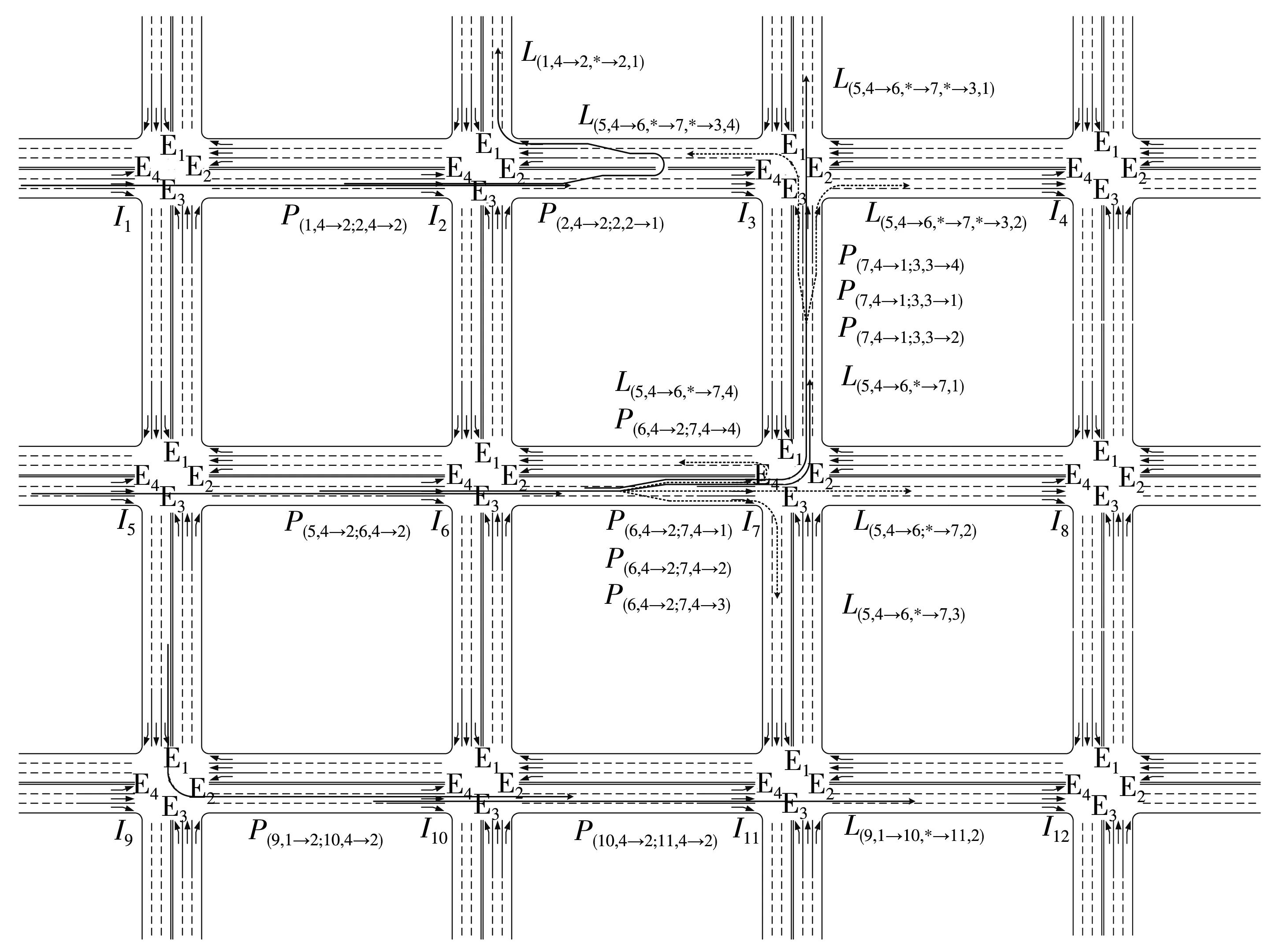
图4 父路径与子路径Fig.4 Parent paths and child paths

1.3 路径链计数方法

由于在路网中存在长度不同、起讫点不同以及中间点不同的路径链，因此对于各种路径链的数量应根据父路径与子路径之间的衍生关系进行分类统计。为讨论方便，文中不对掉头路径链进行统计。

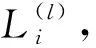
1.3.1 路径数量N1

由于任意一条有向路段的上游交叉口有3种驶入流向，下游交叉口有3种驶出流向(如图5(a)所示的有向路段I1→I2)，故任意一条有向路段存在9条(3×3=9)路径与之对应(如图5(a)中蓝色线段所示)。对于3×3、3×4、4×4、4×5、5×5、……、n×m的方格路网分别存在24、34、48、62、80、……、4nm-2n-2m条有向路段，可以推出路径数量N1的计算公式为

N1=9×(4nm-2n-2m)=36nm-18n-18m

(3)

(n≥3,m≥3)

1.3.2 路径链数量

对于终点处于控制子区范围内的路径与路径链，可以在下游交叉口的3个驶出流向分别生成1条新的路径链，如图4中的L(5,4→6,*→7,1)、L(5,4→6,*→7,2)、L(5,4→6,*→7,3)和L(5,4→6,*→7,*→3,4)、L(5,4→6,*→7,*→3,1)、L(5,4→6,*→7,*→3,2)。对于终点处于控制子区范围外的路径与路径链，则无法连接新的下游路径，此时将停止生成新的路径链，如图5(a)中交叉口I6的E2出口和交叉口I7的E3、E4出口。根据终点处于控制子区范围外的不同位置情况，需要对所涉及的路径与路径链分情况进行讨论。

(1)路径链数量N2

由图5(a)所示的方格路网可见，对于控制子区边界上的顶点交叉口，例如交叉口I7存在2个出口E3与E4无法连接下游路径，由于E3(E4)出口的上游交叉口可以为I4与I8，所对应的上游交叉口驶入流向包括交叉口I4的E1、E2、E4入口和交叉口I8的E1、E2、E3入口，因此对于子区边界上的每一个顶点交叉口，存在12条(2×2×3=12)路径不能生成新的路径链(如图5(a)中绿色线段所示)。对于控制子区边界上的非顶点交叉口，例如交叉口I6存在1个出口E2无法连接下游路径，由于E2出口的上游交叉口可以为I3、I5与I9，所对应的上游交叉口驶入流向包括交叉口I3的E1、E2、E4入口，交叉口I5的E1、E3、E4入口和交叉口I9的E2、E3、E4入口，因此对于子区边界上的每一个非顶点交叉口，存在9条(1×3×3=9)路径不能生成新的路径链(如图5(a)中灰色线段所示)。

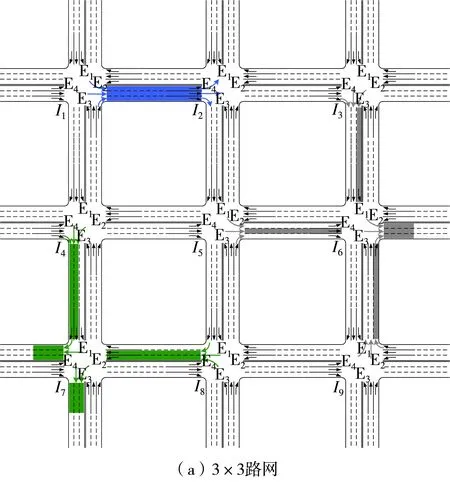
综合起来，对于如图5(a)所示的3×3方格路网，在其子区边界上共有4个顶点交叉口、4个非顶点交叉口，合计将有84条(4×12+4×9=84)路径不能生成新的路径链，因此包含2段路径的路径链数量为396条(3×(216-84)=396)。

对于更大规模如3×4、4×4、4×5、5×5的方格路网，其计算方式类似，由此可以推出n×m的方格路网在其子区边界上共有4个顶点交叉口、2n+2m-8个非顶点交叉口，故其路径链数量N2的计算公式为

N2=3×[N1-4×12-(2n+2m-8)×9]=

3N1-54n-54m+72

(4)

(2)路径链数量N3

与计算路径链数量N2的分析思路类似，需要分别针对控制子区边界上的顶点交叉口与非顶点交叉口，计算不能继续延伸的路径链数量。但需要注意的是，对于不同的路网结构，其边界交叉口出口所不能继续延伸的路径链数量计算公式不尽相同。

例如，对于图5(a)所示的3×3方格路网，控制子区边界上的每一个顶点交叉口都存在2个出口无法连接下游路径，每个出口的上游交叉口可以有4种路径组合，例如对于交叉口I7而言，其上游交叉口路径组合包括I1→I4→I7、I5→I4→I7、I5→I8→I7、I9→I8→I7，而最上游的起始交叉口又有3种驶入流向，因此存在24条(2×4×3=24)路径链不能生成新的路径链。控制子区边界上的每一个非顶点交叉口都存在1个出口无法连接下游路径，每个出口的上游交叉口可以有5种路径组合，例如对于交叉口I6而言，其上游交叉口路径组合包括I2→I3→I6、I2→I5→I6、I4→I5→I6、I8→I5→I6、I8→I9→I6，而最上游的起始交叉口都有3种驶入流向，因此存在15条(1×5×3=15)路径链不能生成新的路径链。综合起来，合计将有156条(4×24+4×15=156)路径链不能生成新的路径链，故包含3段路径的路径链数量为720条(3×(396-156)=720)。

对于图5(b)所示的4×5方格路网，控制子区边界上的每一个顶点交叉口都存在2个出口无法连接下游路径，与3×3方格路网情况类似，因此存在24条(2×4×3=24)路径链不能生成新的路径链。控制子区边界上的每一个非顶点交叉口都存在1个出口无法连接下游路径，但各个出口的上游交叉口路径组合情况却有所不同，需要分类讨论。其中一类交叉口的上游交叉口有6种路径组合(如图5(b)中紫色线段所示)，包括I2、I4、I6、I10、I11、I15、I17、I19共8个交叉口;另一类交叉口的上游交叉口有7种路径组合(如图5(b)中红色线段所示)，包括I3与I18共2个交叉口;同样由于最上游的起始交叉口都有3种驶入流向，因此合计将有282条(4×24+8×1×6×3+2×1×7×3=282)路径链不能生成新的路径链，故包含3段路径的路径链数量为2 934条(3×(1 260-282)=2 934)。

同理，可以计算其他路网结构下的路径链数量N3及N4，如表1所示。如前所述，由于不同路网结构将对控制子区边界上的非顶点交叉口路径链延伸产生不同影响，因此需要根据路径链长度与路网结构，分情况推导路径链数量的计算公式，例如通式f2(n,m)=126n+126m-288(m≥3，n≥3)和通式f3(n,m)=342n+342m-1 008(m≥4，n≥4)。

表1 不同规模路网的路径与路径链数量

2 协调路径集优选方法

2.1 优选法则

为了使协调控制方案能够最大限度地考虑到子区内的行驶车辆，在形成协调路径集时需要综合考虑各条路径链所经过的交叉口数量(路径链长度)和所承载的交通流量。

(1)路径链长度最大

为了尽量保持协调路径之间的连续性，同时兼顾协调控制方案应能获取到的最低实际效益，制定流量约束下基于路径链长度最大的路径集优选法则如下。其中通过设定流量阈值q0可以有效限制协调路径链的长度，以避免出现协调路径链上行驶车流量过小的情形。

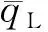
(5)

通过图6所示示例，对流量约束条件下基于路径链长度最大的路径集优选过程分析如下。

图6中：S1、S2、S3、S4、S5、S6分别表示满足流量约束条件的包含1、2、3、4、5、6段协调

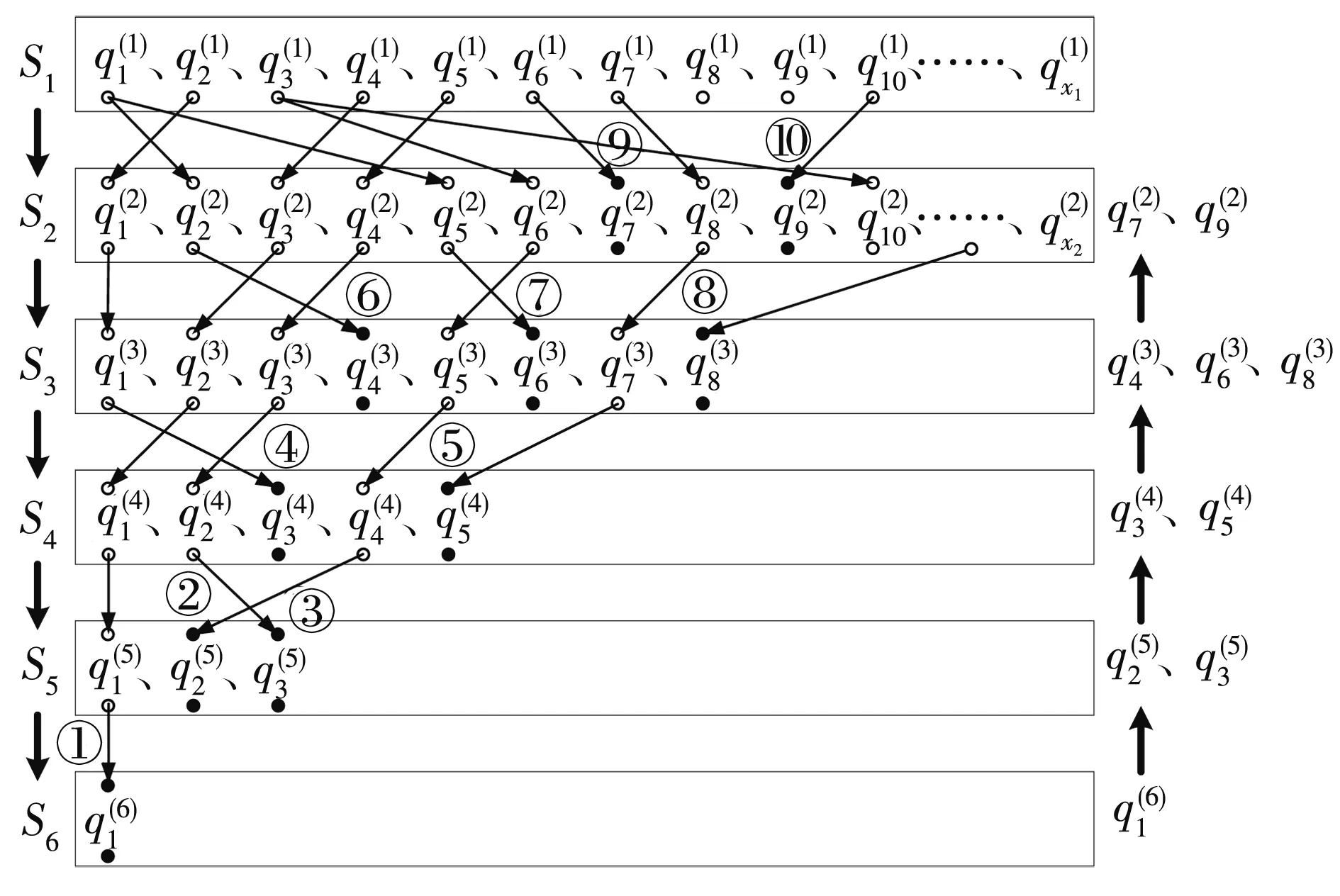
图6 流量约束下基于路径链长度最大的路径集优选示例

(2)路径链总流量最大

为了使得控制子区内尽可能多的行驶车辆获得协调控制效果，同时考虑到交叉口数量增加会逐渐减弱协调设计效果，制定长度约束下基于路径链总流量最大的路径集优选法则如下。其中通过设定长度阈值l0可以直接限定协调路径链的最大长度，以保证获得较好的协调控制效益。

法则2 在满足长度约束条件l≤l0的情况下，选出流量与长度乘积(总流量大小)排名处在前r位的协调路径链构成协调路径集。

对于长度阈值l0，可以根据控制区域的规模或可协调交叉口的数量进行设定。以l0=5为例，通过图7所示示例，对于长度约束下基于路径链总流量(路径链流量与长度乘积)最大的路径集优选过程分析如下。

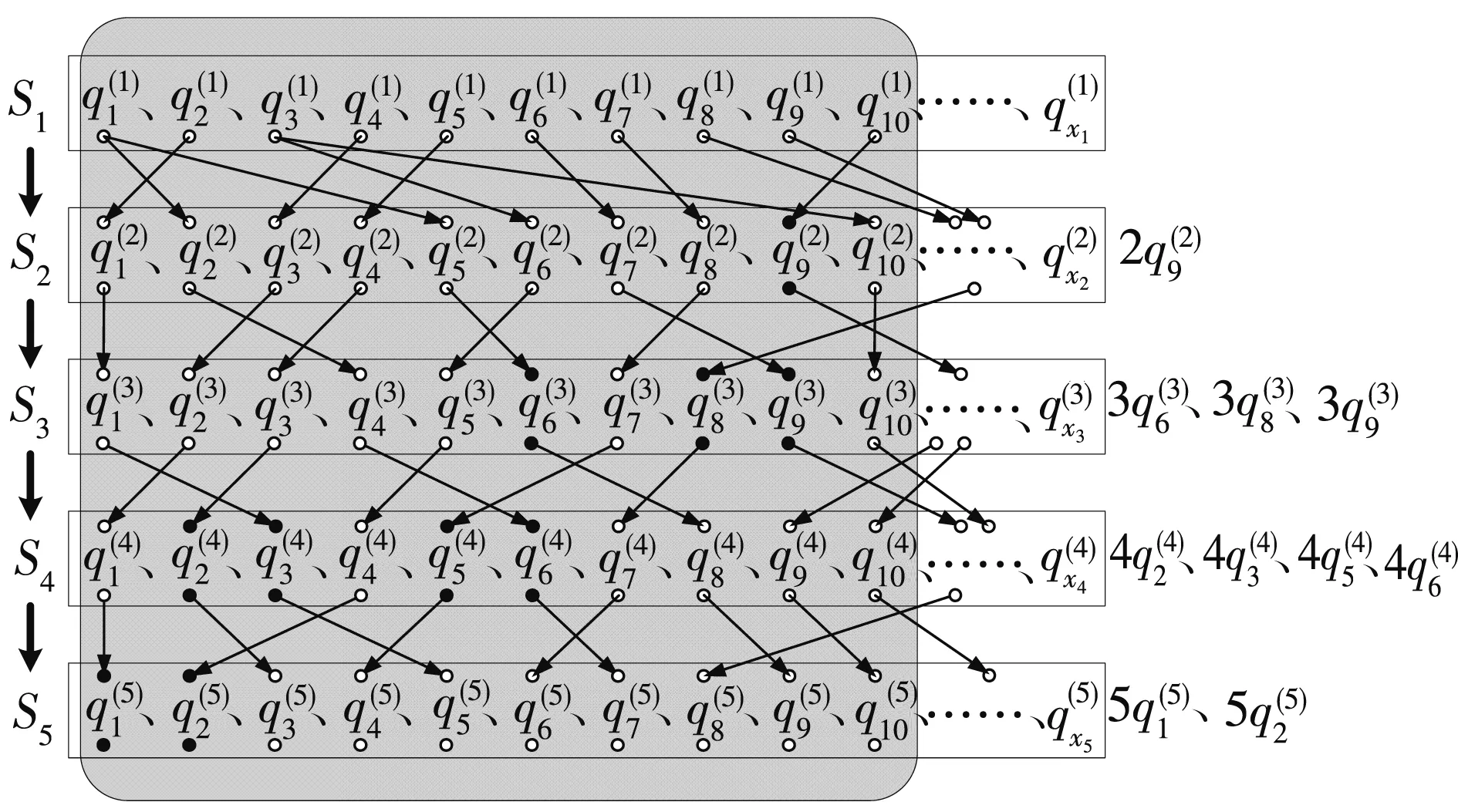
图7 长度约束下基于路径链总流量最大的路径集优选示例

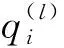
2.2 优选流程

制定法则1“流量约束下基于路径链长度最大的路径集优选”的流程，如图8(a)所示；制定法则2“长度约束下基于路径链总流量最大的路径集优选”的流程，如图8(b)所示。

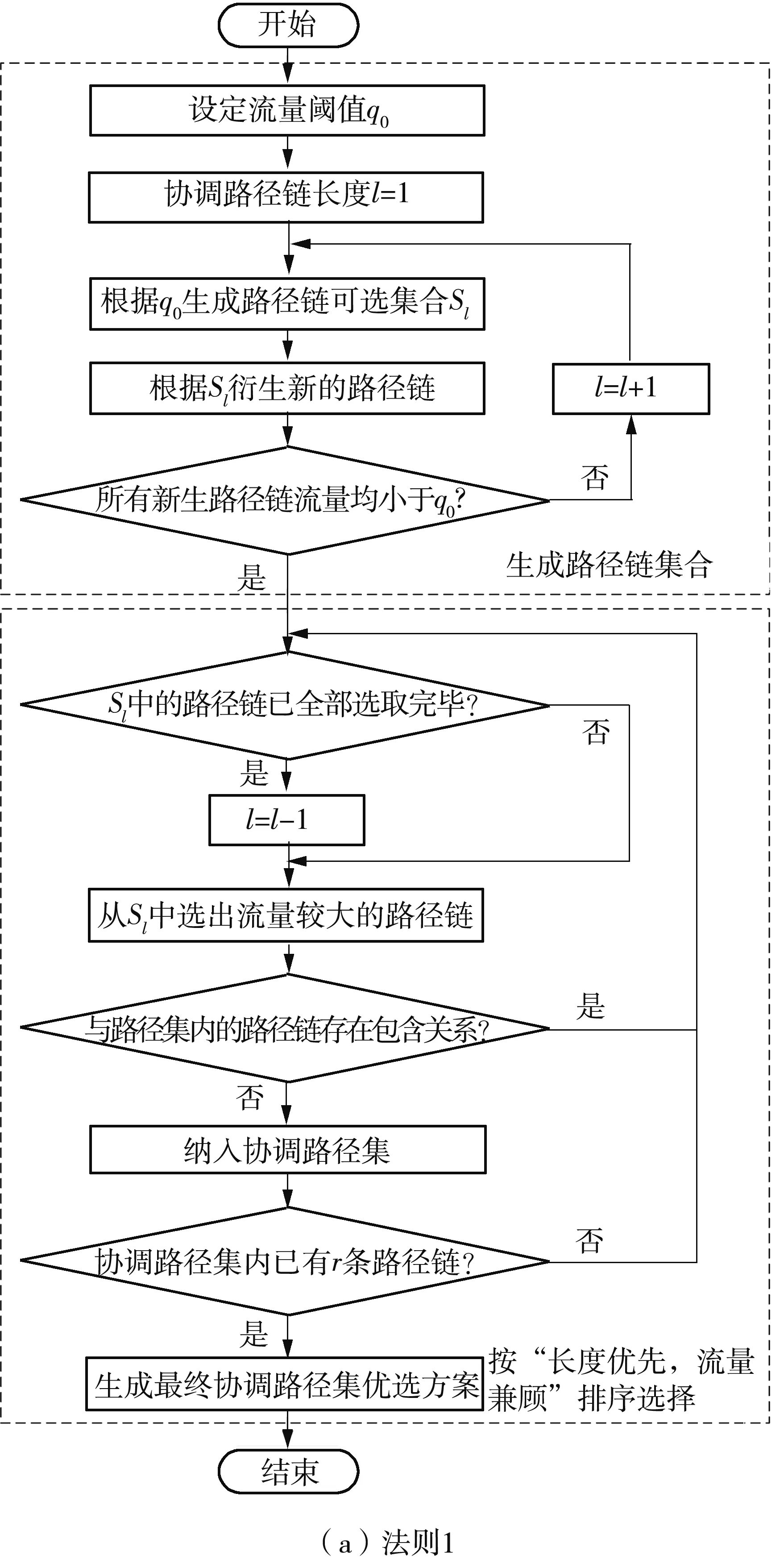
法则1是以路径链流量为约束条件，按“长度优先，流量兼顾”的原则排序生成协调路径集优选方案；法则2则是以路径链长度为约束条件，按“总流量最大”的原则排序生成协调路径集优选方案。可以看到，这两个法则都综合考虑了路径链的长度及其交通流量，但在优选评价指标的选择上存在一定差异。

需要注意的是，在每次选出流量(或总流量)较大的路径链后，均需判断是否与协调路径集内的已有路径链存在包含关系，若不存在，才能纳入协调路径集。

3 算例分析

已知某区域路网由4条东西向干线AEW1、AEW2、AEW3、AEW4与4条南北向干线ASN1、ASN2、ASN3、ASN4交叉形成，其中包含I1、I2、……、I16共16个交叉口，R1、R2、……、R40共40条路段，路网结构如图9所示。

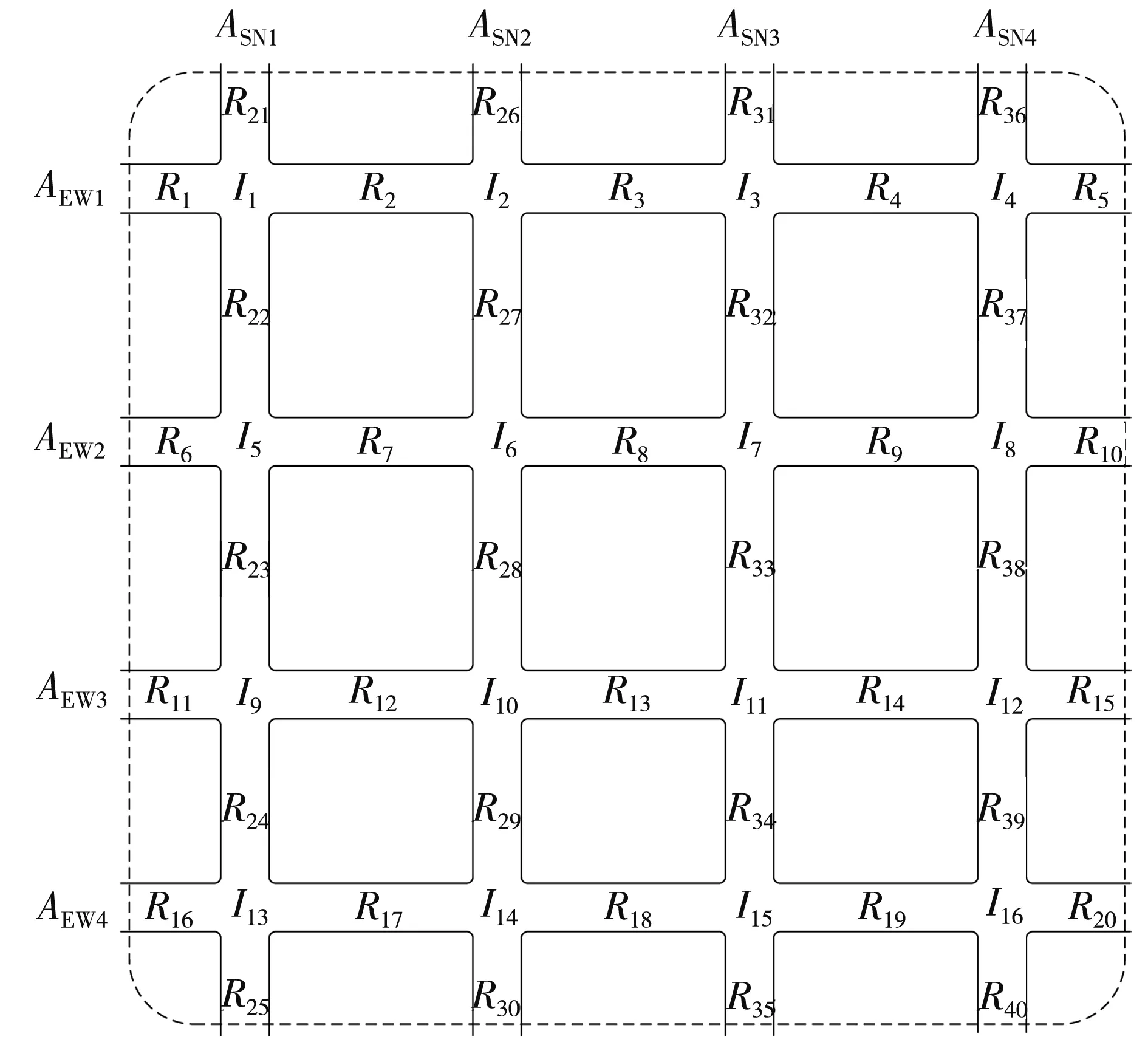
图9 路网结构图Fig.9 Structure of road network

路网边界驶入交通流量及各交叉口交通流量转向比例如表2和表3所示。

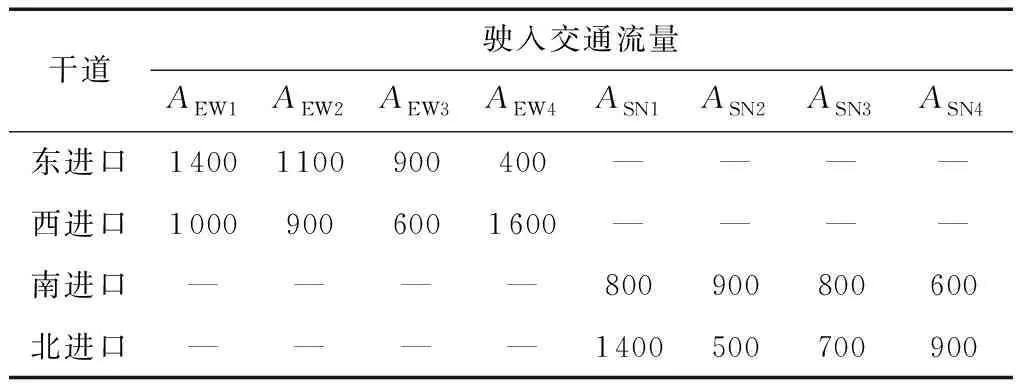
表2 路网边界驶入交通流量

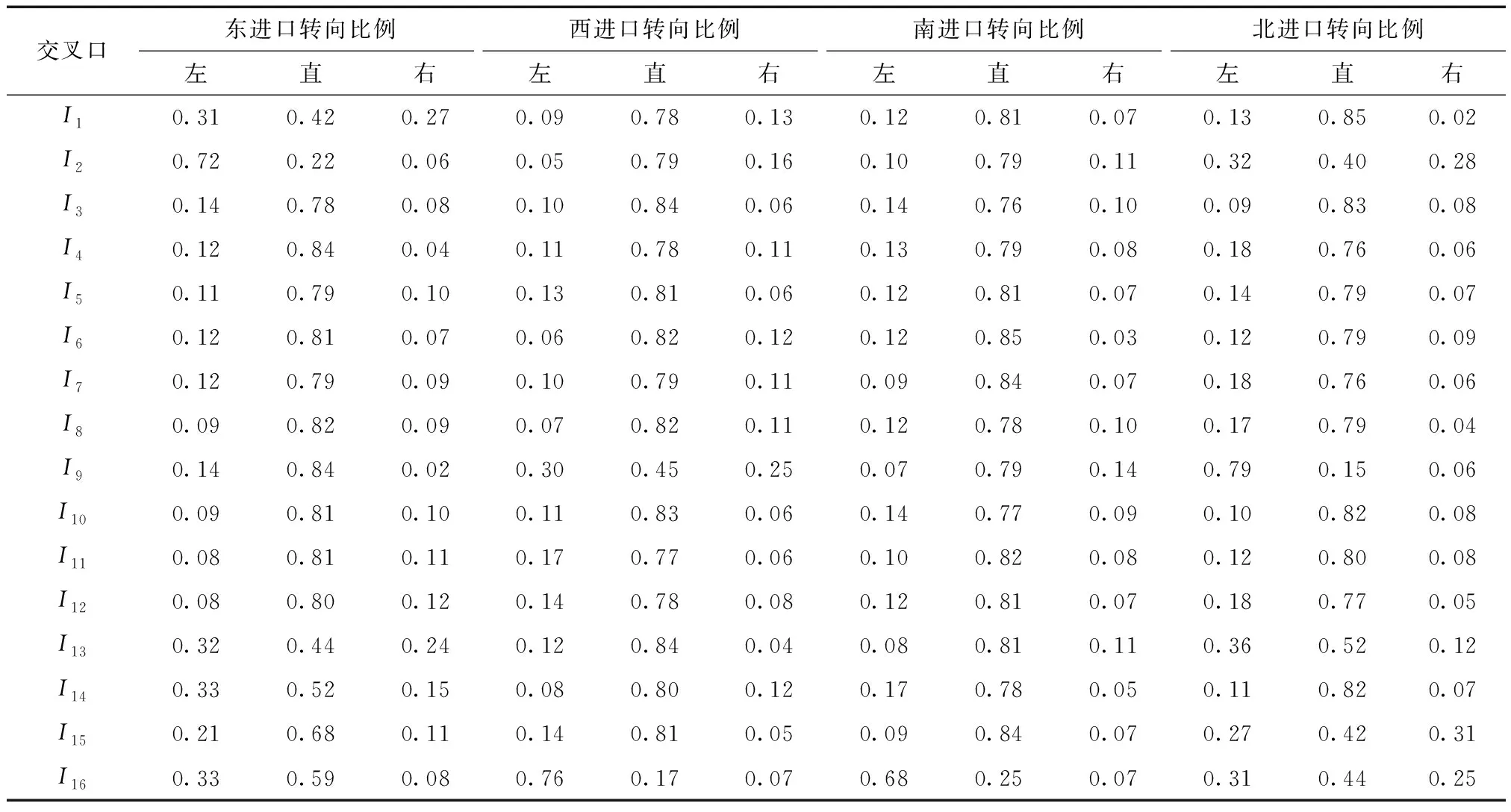
表3 各交叉口交通流量转向比例Table 3 Turn ratio of traffic flow at each intersection

利用Vissim仿真软件建立区域路网，输出车辆轨迹数据。对车辆行驶轨迹进行整理，将流向相同的轨迹线进行合并汇总，形成行驶路径流量示意图，如图10所示。

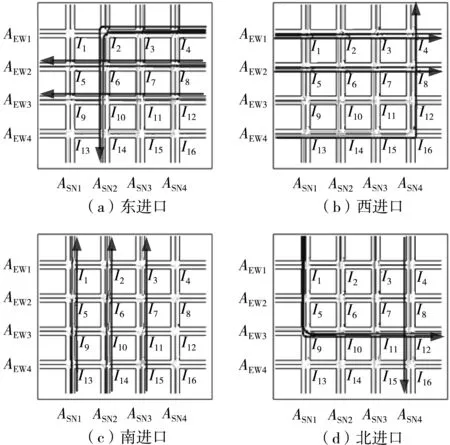
图10 行驶路径流量示意图Fig.10 Schematic diagrams of path flow

图10(a)、10(b)、10(c)、10(d)分别反映了路网中东、西、南、北各个进口方向的车流行驶路径流量大小，轨迹线越宽所对应的车流量越大。从图中可粗略看出，路径链L(4,2→3,*→2,*→6,*→10,*→14,3)、L(8,2→7,*→6,*→5,4)、L(12,2→11,*→10,*→9,4)、L(1,4→ 2,*→3,*→ 4,2)、L(5,4→ 6,*→ 7,*→ 8,2)、L(13,4→14,*→15,*→16,*→12,*→8,*→ 4,1)、L(13,3→ 9,*→ 5,*→ 1,1)、L(14,3→ 10,*→ 6,*→ 2,1)、L(15,3→ 11,*→ 7,*→ 3,1)、L(1,1→5,*→9,*→10,*→11,*→12,2)、L(4,1→8,*→ 12,*→ 16,3)等具有较大流量。

根据路网结构与车辆行驶轨迹数据，分别遵循法则1与法则2，编程求解得到不同流量阈值与长度阈值下的协调路径集优选结果，如图11与图12所示。编程求解过程包括：①遍历轨迹数据，根据车辆ID与时空属性进行排序，获取各个车辆经过的路段ID数据矩阵；②以路网中所有路径作为父路径，通过不断向下游衍生子路径，产生满足约束条件的新路径链；③当不能再产生满足约束条件的路径链时，形成可选路径链集合；④对可选路径链集合中的路径链进行排序，得到协调路径集优选方案。

从图11可以看出：当流量阈值较大时，选取出来的协调路径链之间将存在较多的重复路径，不利于找到更多相对独立的协调线路；随着流量阈值的减小，协调路径链的长度将逐渐增长，此时存在重复路径的路径链也将逐渐减少；当流量阈值减小到一定程度后，协调路径集的优选结果将基本稳定，但流量阈值也不能取值过小，否则可能将过小流量的较长协调路径链也纳入路径集，这样将不利于整个路网取得较大的协调控制效益。从图11也可以看到，不同流量阈值下的协调路径集优选结果与图10中的较大流量路径链基本对应。

从图12可以看出，不同长度阈值下的协调路径集优选结果与图10中的较大流量路径链也基本对应。随着长度阈值的减小，所选协调路径链的长度将逐渐缩短，一些流量较大的路径将重复出现在多条协调路径链上，协调路径集的优选结果最终集中在少数几条协调线路上，如图12(d)所示。

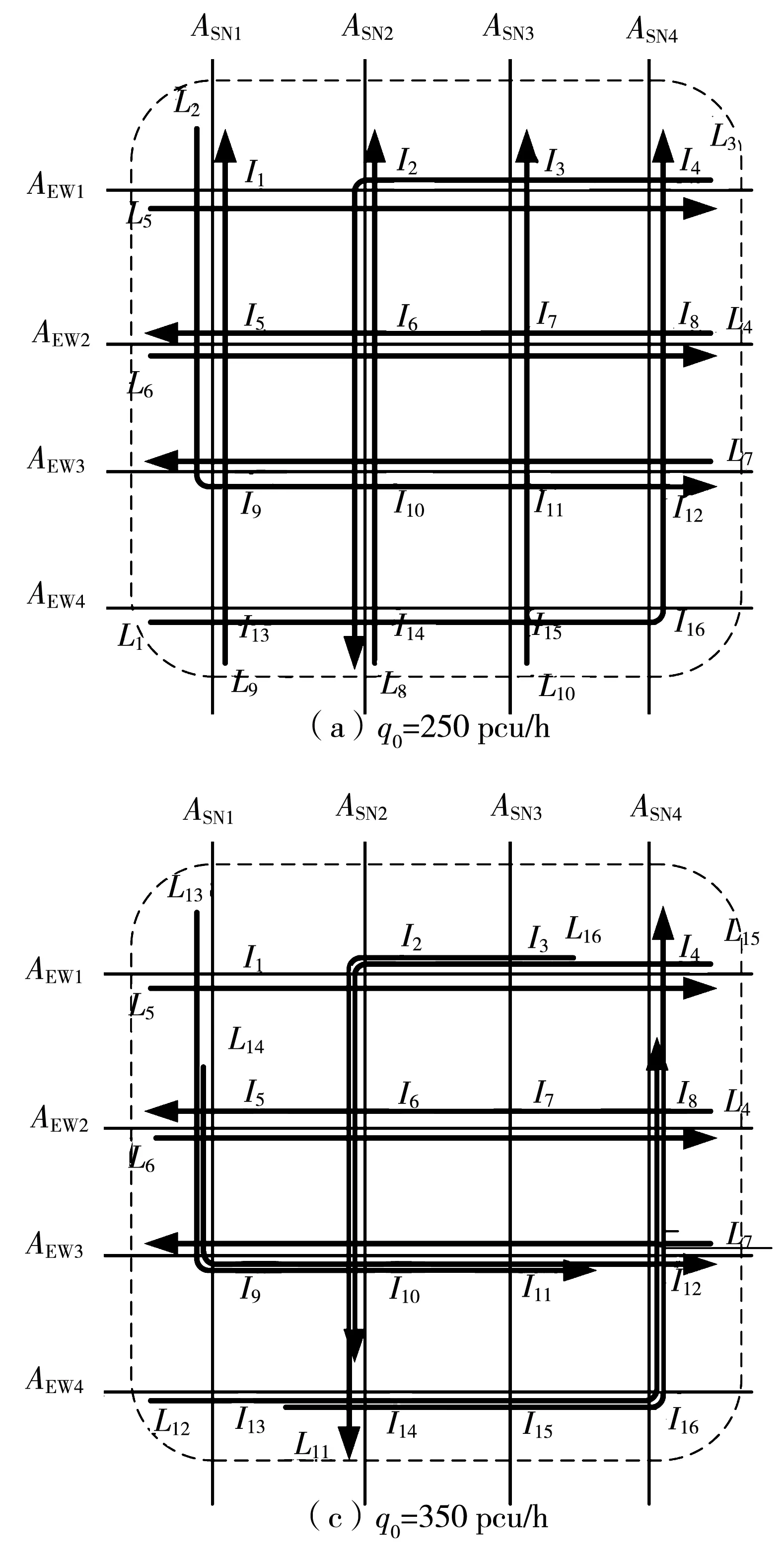
与法则1相比，由于法则2需要对所有路径链的总流量进行排序，因此其运算所需时间更长，且随着长度阈值的增加，法则2的运算量将明显增大；但由于长度阈值的确定较为容易，往往可以根据控制区域规模或可协调交叉口数量直接进行取值，因此法则2的筛选规则更加清晰明确，易于接受与操作。此外，通过对比法则1与法则2的优选结果可以发现，随着流量阈值的减小，法则1可以得到完全不重叠的协调路径集，但对于法则2，调节长度阈值并不能得到完全不重叠的协调路径集。

考虑到实际路网中交通流量变化的波动特性，分别以q0=250 pcu/h与l0=5作为约束条件，分析流量波动对法则1与法则2优选结果的影响。设定区域边界驶入流量分别在5%、10%、20%、40%的波动范围内随机上下波动，各通过10次模拟实验得到流量随机波动下的路径链排名情况，如图13与图14所示。图中，颜色越深表示路径链排名越靠前，其中图13与图11中的路径链L1-L15彼此对应，图14与图12中的路径链L1-L10彼此对应，此外图14的L11=L(14,3→10,*→6,*→2,1)，L12=L(1,1→5,*→9,*→10,2)，L13=L(13,3→9,*→5,*→1,1)，L14=L(14,4→15,*→16,*→12,*→8,*→ 4,1)，L15=L(15,3→11,*→7,*→3,1)。

从图13可以看出：当交通流量在5%的范围内波动时，法则1生成的协调路径集一直保持不变，但协调路径链排名有局部变化；当波动范围扩大到10%时，有2次实验的协调路径集发生略微变化，表现为协调路径链L1因无法达到流量阈值，被拆分为长度略短的协调路径链L11与L12，如图13(b)所示的实验4与实验10；当波动范围扩大到20%时，有3次实验的协调路径集发生变化，表现为协调路径链L1被拆分为L11与L12，协调路径链L2被拆分为L13与L14，协调路径链L3被替换为L15，如图13(c)所示；当波动范围扩大到40%时，则有9次实验的协调路径集发生变化，如图13(d)所示。

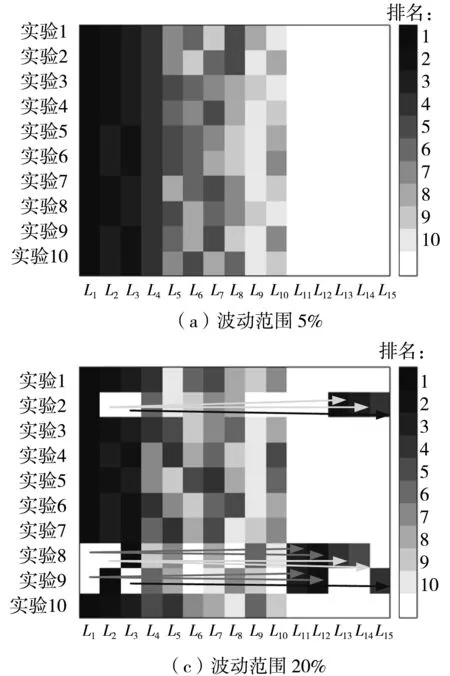
从图14可以看出，当交通流量在5%的范围内波动时，法则2生成的协调路径集就开始发生变化，其中只有4次实验的协调路径集未发生变化，如图14(a)所示。随着交通流量波动范围的逐步增大，协调路径集及其内部路径链排名的变化概率逐渐增大，并且由于优选法则规定协调路径集内任意两条协调路径链之间不存在包含关系，因此出现了两条较短协调路径链合并形成一条总流量更大的较长协调路径链的情况，如图14(a)、14(c)、14(d)所示。

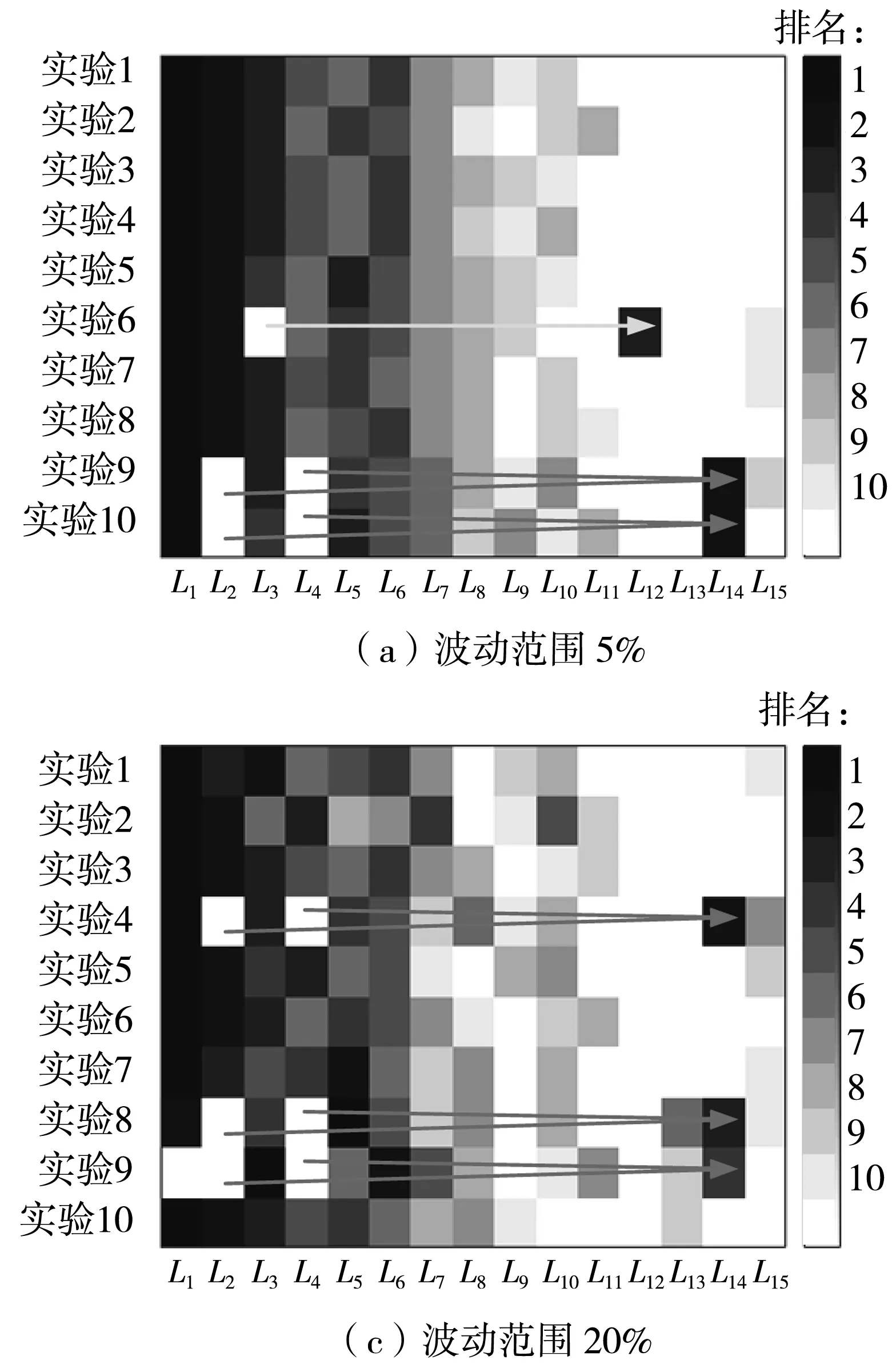
在使用法则1进行协调路径集优选时，为了能够选出尽可能长的协调路径链，将流量阈值设置为较小值(q0=250 pcu/h)，故在流量未发生波动时选出的协调路径链均是较长路径链(如图11(a)所示)，所以当流量发生波动时，仅出现路径链一分为二的情况。在使用法则2进行协调路径集优选时，为了能够选出总流量尽可能大的协调路径链，将长度阈值设置较大(l0=5)，在流量未发生波动时，方案选取了未达到长度阈值的路径链(如图12(b)中的L2、L4)；而在流量发生波动时，方案出现了选取更长路径链的情况，即表现为路径链合二为一(如图14(c)、14(d)中的L14)。

对比图13与图14可以发现，在同一波动等级上利用法则1优选得到的协调路径链排名变化幅度比法则2更小，表现出更好的稳定性。其原因在于，法则1是将流量大小作为路径集优选的约束条件，因此其路径链排名对于流量波动的敏感性较弱；而法则2是将流量大小直接纳入目标函数值计算，因此流量波动对其路径链排名将产生较大影响。

综上可知，上述两种优选方法均能够有效地选出路网中流量较大的路径链，其中流量约束下基于路径链长度最大的路径集优选方法具有计算量小、实时性好、稳定性强等优点，能够最大限度地选取互不重叠的较长协调路径链；长度约束下基于路径链总流量最大的路径集优选方法则具有规则简明、算法简单等优点，能够选取出总流量最大的协调路径链，协调控制效果将更容易得以保障。

4 结语

鉴于现有的交通控制子区划分方法无法反映控制区域内交叉口之间的方向性协调控制需求，文中通过对协调对象进行分解细化，给出了协调路径(包括父路径、子路径)、协调路径链、协调路径集的概念，分析了协调路径链的延伸规律，提出了基于路径链长度及交通量大小的协调路径集优选方法。文中方法能够更加细致地考虑交叉口之间的方向性协调需求，为区域协调控制对象的选取提供了一套新方法。

如何对协调路径集上的交叉口进行信号优化，建立面向协调路径集的区域交通信号控制优化模型，以及考虑控制区域内多种类型车流的协同优化，是后续研究中拟解决的科学问题。