概率问题常见典型考题赏析

■朱云飞

概率是高中数学的重要内容,也是高考的必考内容。高考主要考查随机事件与概率,考查事件的相互独立性以及概率与频率等。下面就概率问题常见典型考题进行举例分析,供大家学习与提高。

题型1:随机事件的表示

理解随机现象、样本点和样本空间的概念,理解随机事件的概念,在实际问题中,能正确求出事件包含的样本点的个数,并会写出相应的样本空间。

例1 抛掷红、蓝两枚骰子的试验,用(x,y)表示结果,其中x表示红色骰子出现的点数,y表示蓝色骰子出现的点数。

(1)写出这个试验的样本空间。

(2)写出这个试验的结果的个数。

(3)指出事件A={(1,6),(2,5),(3,4),(4,3),(5,2),(6,1)}的含义。

(4)写出“点数之和大于8”这一事件的集合表示。

解:(1)这个试验的样本空间Ω为{(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)}。

(2)这个试验的结果的个数为36。

(3)事件A的含义为抛掷红、蓝两枚骰子,掷出的点数之和为7。

(4)记事件B=“点数之和大于8”,则B={(3,6),(4,5),(4,6),(5,4),(5,5),(5,6),(6,3),(6,4),(6,5),(6,6)}。

题型2:随机事件的含义

解答此类问题,应先理解事件中样本点的意义,再观察事件中样本点的规律,才能确定随机事件的含义。

例2 柜子里有3双不同的鞋,随机抽取2只,用A1,A2,B1,B2,C1,C2分别表示3双不同的鞋,其中下标为奇数表示左脚,下标为偶数表示右脚。指出下列随机事件的含义。

(1)事 件M= {A1B1,A1B2,A1C1,A1C2,A2B1,A2B2,A2C1,A2C2,B1C1,B1C2,B2C1,B2C2}。

(2)事件N={A1B1,B1C1,A1C1}。

(3)事件P= {A1B2,A1C2,A2B1,A2C1,B1C2,B2C1}。

解:(1)事件M的含义是“从3双不同鞋中随机抽取2只,取出的2只鞋不成双”。

(2)事件N的含义是“从3 双不同鞋中随机抽取2只,取出的2只鞋都是左脚”。

(3)事件P的含义是“从3 双不同鞋中随机抽取2只,取到的鞋一只是左脚,一只是右脚,但不成双”。

题型3:事件的运算

事件的运算应注意的两个问题:一是要紧扣运算的定义,二是要全面列举同一条件下的试验可能出现的全部结果,必要时可利用Venn图或列出全部的试验结果进行分析。在一些比较简单的题目中,需要判断事件之间的关系时,可以根据常识来判断。如果遇到比较复杂的题目,需要严格按照事件之间关系的定义来推理。

例3 在掷骰子的试验中,可以定义许多事件。例如,事件C1={出现1 点},事件C2={出现2 点},事件C3={出现3 点},事件C4={出现4点},事件C5={出现5点},事件C6={出现6点},事件D1={出现的点数不大于1},事件D2={出现的点数大于3},事件D3={出现的点数小于5},事件E={出现的点数小于7},事件F={出现的点数为偶数},事件G={出现的点数为奇数}。根据上述定义的事件,回答下列问题。

(1)请列举出符合包含关系、相等关系的事件。

(2)利用和事件的定义,判断上述哪些事件是和事件。

解:(1)事件C1,C2,C3,C4发生,则事件D3必发生,所以C1⊆D3,C2⊆D3,C3⊆D3,C4⊆D3。

同理可得:事件E包含事件C1,C2,C3,C4,C5,C6;事件D2包含事件C4,C5,C6;事件F包含事件C2,C4,C6;事件G包含事件C1,C3,C5。

易知事件C1与事件D1相等,即事件C1=D1。

(2)因为事件D2={出现的点数大于3}={出现4点或出现5 点或出现6 点},所以D2=C4∪C5∪C6(或D2=C4+C5+C6)。同理可得:D3=C1∪C2∪C3∪C4,E=C1∪C2∪C3∪C4∪C5∪C6,F=C2∪C4∪C6,G=C1∪C3∪C5。

题型4:互斥事件与对立事件

互斥事件与对立事件的判断是针对两个事件而言的。一次试验中,两个互斥事件有可能都不发生,也可能有一个发生,但不可能两个都发生;两个对立事件必有一个发生,但是不可能两个事件同时发生,也不可能两个事件同时不发生。所以两个事件互斥,它们未必对立;反之,两个事件对立,它们一定互斥。

例4 某县城有甲、乙两种报纸供居民订阅,记事件A为“只订甲报”,事件B为“至少订一种报纸”,事件C为“至多订一种报纸”,事件D为“不订甲报”,事件E为“一种报纸也不订”。判断下列每组事件是不是互斥事件;如果是,再判断它们是不是对立事件。

(1)A与C;(2)B与E;(3)B与D;(4)B与C;(5)C与E。

解:(1)由于事件C“至多订一种报纸”中包括“只订甲报”,即事件A与事件C有可能同时发生,故A与C不是互斥事件。

(2)事件B“至少订一种报纸”与事件E“一种报纸也不订”是不可能同时发生的,故B与E是互斥事件。又事件B与事件E必有一个发生,故B与E是对立事件。

(3)事件B“至少订一种报纸”中包括“只订乙报”,即有可能“不订甲报”,也就是说事件B和事件D有可能同时发生,故B与D不是互斥事件。

(4)事件B“至少订一种报纸”中的可能情况为“只订甲报”“只订乙报”“订甲、乙两种报”。事件C“至多订一种报纸”中的可能情况为“一种报纸也不订”“只订甲报”“只订乙报”。也就是说事件B与事件C可能同时发生,故B与C不是互斥事件。

(5)由(4)的分析知,事件E“一种报纸也不订”是事件C中的一种可能情况,所以事件C与事件E可能同时发生,故C与E不是互斥事件。

题型5:古典概型

解古典概型问题时,要牢牢抓住它的两个特点和计算公式。这类问题的解法多样,技巧性强,解题时需要注意两个问题:试验必须具有古典概型的两大特征,即有限性和等可能性;计算基本事件个数时,要做到不重不漏,可借助坐标系、表格或树状图等列出所有基本事件。

例5 同时投掷两个骰子,向上的点数分别记为a,b,则方程2x2+ax+b=0有两个不等实根的概率为( )。

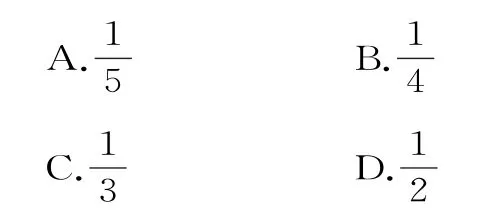
解:因为方程2x2+ax+b=0有两个不等实根,所以Δ=a2-8b>0。

同时投掷两个骰子,向上的点数分别记为a,b,则共包含36个样本点。

题型6:概率的基本性质

当事件A与B互斥(A∩B=∅)时,P(A∪B)=P(A)+P(B),这称为互斥事件的概率加法公式。一般地,如果A1,A2,…,Am是两两互斥的事件,则P(A1∪A2∪…∪Am)=P(A1)+P(A2)+…+P(Am)。若A,B为对立事件,则P(A)=1-P(B)。求复杂事件的概率的两种方法:将所求事件转化成彼此互斥事件的并事件;先求其对立事件的概率,再求所求事件的概率。

解:设“从中任意取出2 粒都是黑子”为事件A,“从中任意取出2 粒都是白子”为事件B,“从中任意取出2 粒恰好是同一色”为事件C,则C=A∪B,且事件A与B互斥。

题型7:相互独立事件的判断

对于事件A,B,若满足P(A∩B)=P(AB)=P(A)P(B),则称事件A,B相互独立,简称A,B独立。所谓独立事件就是某事件发生的概率与其他任何事件都无关,用集合的概念解释即集合之内所有事件发生的可能性范围互不相交。通过式子P(AB)=P(A)P(B)来判断两个事件是否独立,若上式成立,则事件A,B相互独立,这也是定量判断。

例7 一个家庭中有若干个小孩,假定生男孩和生女孩是等可能的,令事件A={一个家庭中既有男孩又有女孩},B={一个家庭中最多有一个女孩}。对下述两种情形,讨论事件A与B的独立性。

(1)家庭中有两个小孩。

(2)家庭中有三个小孩。

由此可知,P(AB)≠P(A)P(B),所以事件A,B不相互独立。

(2)有三个小孩的家庭,男孩、女孩的所有可能情形为Ω={(男,男,男),(男,男,女),(男,女,男),(男,女,女),(女,男,男),(女,男,女),(女,女,男),(女,女,女)},即8个基本事件。

题型8:相互独立事件概率的综合应用

求较复杂事件概率的方法:列出题中涉及的各事件,用适当的符号表示;弄清事件之间的关系(两事件是互斥还是对立,或是相互独立),列出关系式;根据事件之间的关系,准确选取概率公式进行计算。当直接计算符合条件的事件的概率较复杂时,可先间接计算对立事件的概率,再求出符合条件的事件的概率。

因为P(C)>P(B)>P(A),所以丙获得合格证书的可能性最大。

题型9:频率与概率的关系

在实际问题中,常用事件发生的频率作为概率的估计值。在用频率估计概率时,要注意试验次数n不能太小,只有当n很大时,频率才会呈现出规律性,即在某个常数附近波动,且这个常数就是概率。

例9 某公司在过去几年内使用某种型号的灯管1000支,该公司对这些灯管的使用寿命(单位:h)进行了统计,统计结果如表1所示。

表1

(1)求各组的频率。

(2)根据上述统计结果,估计灯管使用寿命不足1500h的概率。

解:(1)由表可知频率依次是0.048,0.121,0.208,0.223,0.193,0.165,0.042。

题型10:随机模拟法估计概率

随机数模拟试验估计概率时,先要确定随机数的范围和用哪些数代表不同的试验结果。可以从以下三个方面考虑:当试验的样本点等可能时,样本点总数即为产生随机数的范围,每个随机数代表一个样本点;研究等可能事件的概率时,用按比例分配的方法确定表示各个结果的数字个数及总个数;当每次试验结果需要n个随机数表示时,要把n个随机数作为一组来处理,此时一定要注意每组中的随机数字能否重复。

例10 某种心脏手术,成功率为0.6,现采用随机模拟方法估计“3 例心脏手术全部成功”的概率。先利用计算器或计算机产生0～9之间取整数值的随机数,由于成功率是0.6,故我们用0,1,2,3 表示手术不成功,4,5,6,7,8,9 表示手术成功;再以每3 个随机数为一组,作为3 例手术的结果。经随机模拟产生如下10组随机数:812,832,569,683,271,989,730,537,925,907。

由此估计“3例心脏手术全部成功”的概率为( )。

A.0.2 B.0.3

C.0.4 D.0.5