时变轴向力负载影响下滚珠丝杠副性能衰退特性

程 强， 计冬雪， 初红艳， 齐宝宝， 郝小龙， 刘志峰

(1.北京工业大学先进制造与智能技术研究所， 北京 100124；2.北京工业大学先进制造技术北京市重点实验室， 北京 100124；3.北京工业大学机械工业重型机床数字化设计与测试技术重点实验室， 北京 100124)

精密滚珠丝杠副具备优良的直线传动性能，在控制系统占据重要地位，因此研究精密滚珠丝杠副性能的衰退十分必要. 滚珠丝杠副的摩擦会造成滚珠丝杠的温度升高，寿命比较短[1-4]. 赵训贵等[5]将预紧力考虑在内建立了丝杠滚珠和滚道间的弹性变形模型. 黄寿荣等[6]研究了复杂工况对滚珠丝杠副摩擦力矩的影响，建立了摩擦力矩模型. 康献民等[7-8]分析了滚珠丝杠的单个滚珠在不同转速、预紧力及轴向载荷下对摩擦力矩波动的影响. 在实际服役过程中，由于机床随着切削参数的变化轴向负载也是变化的，这些具有动态时变特性的工况导致了滚珠丝杠副进给系统精度呈现时变衰退特性. 宋宪春、王兆坦教授等先后对滚道、返向器进行了研究,并设计研发了相关的实验装置[9-12]. 南京理工大学冯虎田、王志荣教授等也在这些方面进行了深入的研究[13-15]，建立了滚珠丝杠副行程误差模型，提出了一种考虑加速度来描述滚珠丝杠磨损特性的经验模型，并提出了滚珠丝杠副各项性能指标的具体测试标准. Chung等[16]对滚珠丝杠副接触变形引起的刚度变化进行分析，建立了接触变形时的刚度模型. Oyanguren等[17]通过对不同预紧力、不同工况下的滚珠丝杠进给系统建模，模拟分析了进给系统的动态性能.

综上所述，研究者对滚珠丝杠的性能进行了大量研究，但是对时变轴向力加载工况下滚珠丝杠性能衰退方面的研究很少. 本文在时变轴向力加载的基础上建立双螺母滚珠丝杠副的受力模型、磨损模型、预紧力的衰退模型和摩擦力矩衰退模型，并通过滚珠丝杠副精度保持性试验台测量序进轴向力加载与恒定轴向力加载工况下的滚珠丝杠磨损深度变化情况，与理论模型对比，从而验证了滚珠丝杠副时变轴向力加载工况下性能衰退模型的有效性与合理性，进而通过理论模型预测预紧力和摩擦力矩的变化. 深入地研究了时变轴向加载工况下滚珠丝杠性能衰退试验的统计分析方法，以期获得效率高且估计精度高的加载方式分析结论，为深入研究时变机床工程用机械设备和试验技术提供理论参考.

1 滚珠丝杠副的接触特性

1.1 时变受力与时变接触变性模型

对于预紧力作用下的双螺母滚珠丝杠副，加载情况如图1所示，在承受时变轴向工作载荷F(t)时，预设左螺母为工作螺母，右螺母为预紧螺母，则左螺母的实际受力相对于原来的预紧力Fp增加预紧螺母产生的时变弹性恢复力F′(t)，左螺母实际受力为FA(t)，则右螺母的实际受力相对于原来的预紧力Fp减小预紧螺母产生的弹性恢复力F′(t)，右螺母实际受力为FB(t)，FA(t)和FB(t)跟随时变轴向工作载荷F(t)变化，因此有

图1 滚珠丝杠副时变轴向加载示意图

FA(t)=Fp+F(t)-F′(t)

(1)

FB(t)=Fp-F′(t)

(2)

δA(t)、δB(t)分别为在预紧力Fp和载荷时变轴向工作载荷F(t)共同作用下2个螺母产生的随着轴向力变化而变化的轴向接触变形量，由Hertz弹性接触理论可得出

(3)

(4)

δP为预紧力Fp对2个螺母产生的轴向接触变形量，δ1(t)为左螺母压缩变形量，δ2(t)为右螺母弹性恢复变形量，由hertz弹性接触理论可得出

(5)

(6)

(7)

按照变形协调方程变形相等原理，压缩变形量δ1(t)与弹性恢复变形量δ2(t)应相等，即

(8)

将滚珠丝杠时变受力模型(1)～(8)用Matlab计算，轴向力F(t)是自变量，加载方式为序进时变载荷(如图2所示)，左螺母受力FA(t)和右螺母受力FB(t)是因变量，根据计算可知，FA(t)和FB(t)随着轴向力F(t)变化而变化，FA(t)随F(t)增加而增加，FB(t)随F(t)增加而降低，FA(t)上升速度大于FB(t)的下降速度.

滚珠丝杠的时变加载工况下的时变轴向力与时变法向力的关系为

(9)

1.2 滚珠丝杠临界载荷

结合赵哲[18]和顾旻杰等[19]根据滚珠丝杠副材料特性确定Mises屈服准则的研究，可得到单个滚珠与滚道刚达到屈服极限时临界法向载荷为

(10)

在最大载荷内是弹性变形，在最大载荷外就会产生塑性变形.式中：σs为材料的屈服极限；kst为0.300～0.325的一个常数；对于滚珠与滚道之间的弹性接触，a*3和b*3分别为滚珠与滚道接触椭圆长、短半轴的量纲为1的系数；∑ρ为滚珠与滚道接触点的主曲率和；E′为等效弹性模量.其中长、短半轴的量纲为1的系数a*3和b*3可以分别表示为

(11)

(12)

K(k)、E(k)分别为第1类、第2类完全椭圆积分，k为椭圆参数，为了简化计算，Hamrock和Brewe给出了K(k)、E(k)、k的近似表达式[20]，根据近似表达式计算的误差将不超过3%，分别为

(13)

等效弹性模量E′表示为

(14)

式中：E1、E2分别为滚珠丝杠接触和滚珠螺母接触的弹性模量；μ1、μ2分别为两接触物体的泊松比.丝杠、螺母、滚珠弹性模量和泊松比相等.

在考虑螺旋升角的情况下，滚珠与丝杠滚道接触点处的曲率半径通过计算主曲率可以表示为

(15)

式中：rb为滚珠半径；rm为丝杠半径；ri为滚道半径.滚珠与丝杠滚道接触点处主曲率之和

(16)

在考虑螺旋升角的情况下，滚珠与丝杠滚道接触点处的曲率半径通过计算主曲率可以表示为

(17)

滚珠与螺母滚道接触点处主曲率之和

(18)

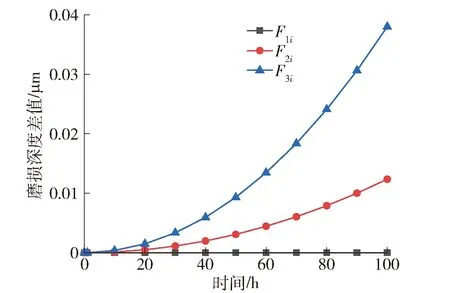
双螺母滚珠丝杠参数如表1所示.经计算，滚珠和丝杠滚道接触的最大接触载荷Qsmax为1 086.3 N，可以推算出滚珠丝杠副所施加的临界轴向载荷F1max为87 288.5 N；滚珠和螺母滚道接触的最大接触载荷Qnmax为1 536.7 N，可以推算出滚珠丝杠副所施加的临界轴向载荷F2max为123 482.5 N.F1max

表1 双螺母滚珠丝杠参数

2 时变工况下滚珠丝杠副性能衰退模型

在时变轴向力加载模型的基础上，本节在Achard理论基础上建立了时变轴向力加载工况下的丝杠滚道和螺母滚道的磨损模型、滚珠丝杠副的时变预紧力衰减模型和时变摩擦力矩衰退模型，由此可以预测在时变轴向力加载工况下丝杠和螺母滚道的预紧力衰退和磨损深度变化规律.

滚珠丝杠运动时既有滚动也有滑动，根据Lin等[21]的研究，在时变轴向力加载模型的基础上工作螺母中滚珠对于丝杠的时变滑动速度为

(19)

工作螺母中滚珠对于螺母时变滑动速度为

(20)

预紧螺母中滚珠对于丝杠时变滑动速度为

(21)

预紧螺母中滚珠对于螺母时变滑动速度为

(22)

将载荷细分，设试验一共使用n步载荷，当t=0时，初始工况参数如下：

F(t)=F1(F1=4 kN)，V(t)=0，δ(t)=0，经式(1)～(8)可计算得出FA(t)和FB(t)的初始值.基于Zhou等[22]理论和杨雪[23]对滚珠丝杠副磨损的研究，工作螺母中滚珠与丝杠滚道时变磨损深度和滚珠与螺母滚道接触面的时变磨损深度分别表示为

(23)

式中：K为黏着磨损系数，取10-6～10-7[23]；H为较软材料的硬度；Ls表示丝杠的有效行程，取300 mm；LN表示螺母的有效行程，取80 mm.

纯林中针叶树种和阔叶树种的碳储量构成：针叶树碳储量2649289 t，阔叶树碳储量494519 t。针叶树碳储量是阔叶树碳储量的5.36倍。针叶树种平均碳密度39.96 t·hm-2，阔叶树种平均碳密度37.30 t·hm-2。详见表3。

时变轴向加载工况下工作螺母中的滚珠与丝杠、螺母接触椭圆面的时变长半轴分别表示为

(24)

与丝杠滚道接触面的时变磨损深度和预紧螺母中滚珠与螺母滚道接触面的时变磨损深度可以分别表示为

(25)

时变轴向加载工况下预紧螺母中的滚珠与丝杠、螺母接触椭圆面的时变长半轴表示为

(26)

所以，滚珠与滚道间接触表面由于磨损所造成的2个表面在垂直接触面方向的位移变化量Δδ′(t)表示为

(27)

2个螺母之间的轴向间距发生改变后的相对轴向总位移Δδ(t)为

(28)

在时变轴向力加载模型和束芳婷等[24]建立的滚珠滚道磨损模型的基础上，建立时变预紧力下降模型

(29)

定义滚珠与丝杠和螺母滚道相互接触的变形系数为ks、kn，可以分别表示为

(30)

在时变轴向力加载模型的基础上，根据预紧力和摩擦力矩的经验公式，建立时变摩擦力矩，可表示为

(31)

3 轴向力加载方案

选择时变轴向力中的序进应力制定了双螺母滚珠丝杠副序进轴向力加载方案，序进轴向力加载方案如图2所示，试验应力从某一初始应力F1开始一直保持线性增加，直到试验结束刚好达到最大值F2，即

图2 序加轴向力加载方案

F(t)=F1+kt

(32)

由于序进轴向力的加载准确度较低，本文提出用步加代替序加.序加与步加试验的统计模型是利用恒加试验的模型建立的，序进应力相当于步进应力的极限形式，即步数趋近于无穷大，则每步应力水平间隔与每步持续时间都趋近于0.序进应力随时间线性增加，初始应力与最终应力为F1和F2，试验总时间为ts，应力上升斜率可以表达为

k=(F2-F1)/ts

(33)

设试验一共使用n步载荷，每步加载时间相同，即

T=ts/n

(34)

设每步的应力

Fi=F1+(i-0.5)kT，i=1，2，3,…,n

(35)

将式(33)(34)代入式(35)，故

Fi=F1+(i-0.5)(F2-F1)/n，i=1，2，3，…，n

(36)

由式(36)可知，对于代替序进应力的步进应力，除了每步的时间间隔相同外，每步的应力间隔也是相同的，为ΔF=(F2-F1)/n，故步进应力为阶梯应力，如图3所示.

图3 阶梯应力

施加轴向力应高于基准载荷,避免施加载荷过小导致性能衰退过慢，看不出效果. 根据相关文献[25]，定义滚珠丝杠副10%的额定动载荷为基准载荷；因为轴向加载超过30%额定动载荷，双螺母中工作螺母受力过大会挣开，只有预紧螺母工作，所以本文选取应力上限为30%的额定动载荷，应力设置上下限在理论上满足加速应力设置的要求即10%和30%，则失效机理不发生变化.

4 试验过程

4.1 滚珠丝杠性能退化试验测试

试验采用的双螺母预紧式滚珠丝杠副结构参数如表1所示，预紧力预设值为3.7 kN.

本文中讨论的时变轴向加载方案为线性增加，将其称为斜坡试验. 设置3组试验，实施方案如表2所示，在100 h内、转速为400 r/min的条件下，轴向力F1i为4 kN恒定不变，轴向力F2i由4 kN直线上升至6 kN，轴向力F3i由4 kN直线上升至8 kN.

表2 加速退化试验方案

序加试验一共使用100步载荷，每步加载时间相同，代入式(36)，则3组斜坡试验的时变轴向力表达式为

(37)

试验装置结构图如图4所示，实物图如图5所示，该试验测试平台具有实现模拟时变轴向负载、径向负载、进给速率、进给行程等功能. 试验台加载系统采用液压静压加载，自制液压站作为动力源，液压油源经过高精度比例伺服阀通过液压油管道连接至轴向液压加载油缸上，轴向液压加载油缸加载U轴驱动丝杠副与X轴滚珠丝杠副，高精度比例伺服阀内置放大器及阀芯位移传感器，高精度比例伺服阀、力传感器与PLC控制柜连接，PLC控制柜与计算机连接. 加载过程中，在计算机屏幕输入加载目标，比如三角函数、阶梯函数、三角波函数曲线，高精度力传感器实时采集加载力的实际值并反馈到PLC控制柜，与输入的指令值比较后，通过高精度比例伺服阀内置的放大器运算后，控制高精度比例伺服的开口，来控制作用轴向液压油缸上的油压，油压来控制轴向液压加载油缸向外运动与运动拖板产生相互作用力，从而对U轴驱动丝杠副施加轴向力，实现较高的加载精度.

1—床身； 2—线性导轨； 3—X轴交流伺服电机； 4—U轴交流伺服电机； 5—施力拖板； 6—轴向液压加载油缸； 7—力传感器； 8—运动拖板； 9—左横梁支撑臂； 10—横梁； 11—横梁盖板； 12—X轴滚珠丝杠副； 13—X轴轴承； 14—X轴轴承套； 15—U轴轴承套； 16—轴承支架； 17—U轴轴承； 18—U轴驱动丝杠副； 19—右横梁支撑臂； 20—螺栓； 21—线性滑块； 22—控制柜； 23—高精度比例伺服阀； 24—压力表； 25—液压油源； 26—PLC控制箱; 27—计算机.

图5 实验装置实物图

时变轴向力工况下滚珠丝杠副试验装置加载系统采用液压静压加载，自制液压站作为动力源，通过高精度比例伺服阀控制轴向液压加载油缸进行加载，通过控制阀芯开口大小控制油压从而控制轴向载荷，实现工作可靠控制精度高.

试验装置加载过程中，高精度比例伺服阀内置放大器及阀芯位移传感器，通过力传感器将轴向液压加载油缸的力反馈给PLC控制箱，PLC控制箱控制与电脑输入的模拟航天工况的函数信号进行比对从而控制比例伺服的开口，实现试验台工况模拟的高度一致.

试验步骤如下.

1) 测试滚珠丝杠副初始定位误差，测量行程为300 mm.

2) 初始工况预紧力设置为3.7 kN，温度为25 ℃，根据表2加速退化方案分别设置轴向负载、转速、加载时长.

3) 开始进行试验.

4) 每10 h用激光干涉仪采集并记录滚珠丝杠副的定位误差.

5) 验证试验周期为100 h，记录滚珠丝杠副的定位误差.

6) 将经磨损之后的定位误差与原始定位误差进行处理与分析，获得磨损前后的定位精度差值，即测试行程内总的磨损深度，将其等效为每个滚珠与滚道之间的磨损深度值.

4.2 试验结果与分析

预紧力退化量决定滚珠丝杠副轴向刚度和定位精度是否满足其使用要求. 由于试验中斜坡加载力差距较小，因此结合做差法来研究其具体趋势.

用Matlab对双螺母滚珠丝杠进行时变轴向力加载性能退化数值仿真，根据磨损深度计算模型仿真得到测试行程内总磨损深度曲线如图6所示，可以看出滚道磨损量随时间增加而增加，在相同时间内，时变轴向力坡度大的滚珠丝杠副磨损量大于坡度小的磨损量. 坡度为F2i和坡度为F3i的磨损量减去恒定轴向力F1i的磨损量，得到的磨损量差曲线如图7所示，可知随着轴向力线性增加，磨损量相对急剧增加.

图6 不同坡度轴向力滚道磨损量曲线

图7 不同坡度与恒定轴向力滚道磨损量差值曲线

将时变轴向力影响下的磨损深度理论计算与试验测试进行对比验证,如图8所示，对不同坡度轴向力加载工况下的磨损深度进行初步的对比,通过时变轴向力加载工况下的磨损深度试验与理论对比验证建立的时变模型有效. 验证了建立的时变轴向力工况下滚珠丝杠副的磨损模型正确性,把握滚珠丝杠副的磨损规律，为研究滚珠丝杠副的磨损规律以及滚珠丝杠副的进给系统进给精度的保持性分析打下了理论基础. 将此验证结果应用至预紧力(即式(29))及摩擦力矩(即式(31))的预测中.

图8 不同坡度轴向力滚道磨损量理论与试验对比差值曲线

根据时变预紧力衰退公式(29)，预紧力会随着滚道磨损量增加而逐渐衰减，根据时变预紧力衰退模型仿真可得到预紧力衰退曲线，如图9所示，可以看出预紧力随时间增加而衰退，在相同时间内，时变轴向力坡度大的预紧力衰退大于坡度小的预紧力衰退.坡度为F2i和坡度为F3i的预紧力衰退量减去恒定轴向力F1i的预紧力衰退量，得到的预紧力差值曲线如图10所示，可知随着轴向力线性增加，预紧力衰退量相对急剧增加.

图9 预紧力退化曲线

图10 预紧力退化差值曲线

根据时变摩擦力矩模型(31)可得到摩擦力矩衰退曲线，如图11所示，可以看出摩擦力矩随时间增加而衰退，在相同时间内，时变轴向力坡度大的摩擦力矩衰退大于坡度小的摩擦力矩衰退.坡度为F2i和坡度为F3i的摩擦力矩衰退量减去恒定轴向力F1i的摩擦力矩衰退量，得到的摩擦力矩差值曲线如图12所示，可知随着轴向力线性增加，摩擦力矩衰退量相对急剧增加.

图11 摩擦力矩退化曲线

图12 摩擦力矩退化差值曲线

由仿真数据可知：在F1i的作用下，摩擦力矩和预紧力在64 h衰退30%；在F2i的作用下，摩擦力矩和预紧力在62 h衰退30%，滚珠丝杠副性能加速退化3.1%；F3i的作用下，摩擦力矩和预紧力在61 h衰退30%，滚珠丝杠副性能加速退化4.7%.

5 结语

在滚珠丝杠副实际服役过程中，包括加速启动、稳定进给、减速停止以及不同加工切削力要求等进给工况中负载具有时变特性，导致性能衰退规律不断变化.本文研究时变轴向力加载工况下滚珠丝杠副进给系统性能时变衰退特性，主要研究成果如下：

1) 建立了时变轴向力加载的滚珠丝杠时变受力模型、时变磨损模型、时变预紧力衰退模型，通过试验验证的方式，验证了磨损深度理论模型的正确性，有利于预测预紧力与摩擦力矩的衰退.

2) 在相同时间内，时变轴向力坡度大的预紧力衰退量和摩擦力矩衰退量大于坡度小的预紧力衰退量和摩擦力矩衰退.随着轴向力线性增加，预紧力的衰退量和摩擦力矩衰退量相对急剧增加.

3) 根据在F1i、F2i、F3i的作用下，摩擦力矩、预紧力的衰退量，可得出滚珠丝杠在实际运行中，轴向力时变产生值越大，滚珠丝杠性能衰退越快.

需要指出的是本文中只试验验证了滚珠丝杠时变磨损深度模型，后续还需要购买器材试验求证时变预紧力衰退模型和时变摩擦力矩衰退模型，并且会继续提高改进试验台时变轴向力加载精度.