均匀场磁感应断层成像系统设计与仿真研究

齐宏波，杜 强，柯 丽，陈 红

（沈阳工业大学电气工程学院，沈阳 110870）

0 引言

磁感应断层成像（magnetic induction tomography，MIT）技术是20 世纪80 年代发展起来的基于电磁感应原理的新型过程层析成像技术[1]，其利用涡流原理，根据被测体中不同组织具有不同的阻抗特性，将激励磁场通过被测体，测量检测线圈的电压相位信号，从而得到被测体中的阻抗分布信息，进而完成被测体介质分布图像的重建[2]。

传统的MIT 系统多采用圆形激励线圈，激励线圈产生的磁场衰减速度快，尤其在被测体深层区域激励能量的幅值很低[3]，因此被测体深层的检测结果的准确率比较低。国内外针对如何提升MIT 系统检测深度的问题进行了很多研究。Li 等[4]利用实验数据研究了平面传感器阵列MIT 系统的性能，由各向同性和各向异性总变分（total variation，TV）获得的重建图像，能够精确地显示样本的位置和形状，验证了平面传感器阵列MIT 系统的深度检测能力，同时验证了各向同性和各向异性TV 算法比Tikhonov 正则化算法能产生更高质量的重建图像。张敬因等[5]提出用8 字形线圈作为激励线圈的设计方案，8 字形激励线圈聚焦了导体内的电磁能量，有效提高了涡流检测的深度。Guadagnin 等[6]研究发现，双锥形激励线圈的系统产生的电磁场能量可激励到更深的程度，系统产生的电磁场能量可刺激到白质以下直到小脑的位置，但电磁场能量的聚焦特性有待进一步提高。Klein等[7]设计了一种三维MIT 系统，在低导电性和体积较大的物体内部改善了中心区域的性能。刘锐岗等[8]设计了以2 个圆形线圈作为激励端的MIT 系统，双激励线圈在夹角为30°、60°、90°时，模型中心处的激励磁场强度约是单线圈MIT 系统激励下的2 倍，但夹角在180°时，磁感应强度小了一个数量级。

如何有效地增强被测体磁感应信号，是将MIT技术应用到临床上的关键。为增强磁感应信号，本文设计一种以亥姆霍兹线圈作为激励端的均匀场MIT系统，并通过仿真实验对MIT 系统与传统系统进行对比评估。

1 磁感应信号增强方法

1.1 MIT 原理分析

MIT 系统得到的信号为相位差数据，激励磁场B0作用于被测体，被测体产生感生涡流，从而感生二次磁场ΔB，二次磁场与激励磁场叠加，主磁场B 发生相位偏移[9]。MIT 中真正有效的信号为涡流产生的二次磁场信号ΔB，而其信号强度相对于激励磁场B0很低，在激励磁场的背景下检测精度并不高，这对于MIT 的成像质量造成了很大影响。为了提高二次磁场的强度，需要提高被测体中的因激励磁场产生的涡流强度。当保持激励磁场频率不变时，提高磁场强度或提升磁通量变化率就可实现涡流强度的提升。因此，被测体内部磁场强度的大小直接决定了MIT的成像质量。然而，当激励磁场强度整体提升时，虽然二次磁场强度有所提高，但是由于激励磁场B0的增强，被测体中心的检测精度并不能提升。因此，改变激励磁场分布，提高其在被测体深层与表面的磁场强度分布均匀性是解决磁感应信号弱的关键。

1.2 均匀场对磁感应信号的增强作用

MIT 中灵敏度矩阵通常定义为边界测量电压的变化和引起该变化的物场空间中某个单元像素上的电磁参数变化之比[10]。根据这一基本原理，采用场量提取的方法计算MIT 系统的灵敏度[11]。假设整个成像系统的边界足够远，可以包围整个电磁敏感场，那么MIT 系统中电导率、磁导率等各个物理参数的灵敏度值可以由公式（1）～（3）得到：

式中，Sσ、Sμ、Sε分别为MIT 系统中边界测量值对于电导率σ、磁导率μ 和介电常数ε 的灵敏度；EA和EB分别为激励线圈和检测线圈在单位电流激励时的电场分布，HA和HB分别为激励线圈和检测线圈在单位电流激励时的磁场强度分布；ω 为系统施加的激励信号频率。

针对MIT 系统灵敏度场的中心处灵敏度值较低，即中心磁感应信号差的问题，本文对传统MIT 系统的灵敏度进行研究。通过COMSOL 仿真软件，采用有限元方法，对研究中涉及的各情况进行有限元仿真及计算分析。传统MIT 系统多采用单线圈的激励方式，即采用1 个线圈通以激励电信号作为系统激励，该形式避免了不同激励线圈之间的耦合效应，并且其产生的激励磁场也较为简单，有利于后续的图像重建。本文建立传统MIT 模型，并对该模型进行仿真。

通过仿真计算得出成像系统边界内的电磁场分布情况，提取仿真结果中的数据，根据公式（1）～（3）计算不同激励检测线圈对下的系统灵敏度场。图1为传统激励场下的MIT 系统灵敏度场，由图1 可以看出传统MIT 系统中的灵敏度场具有以下特性：

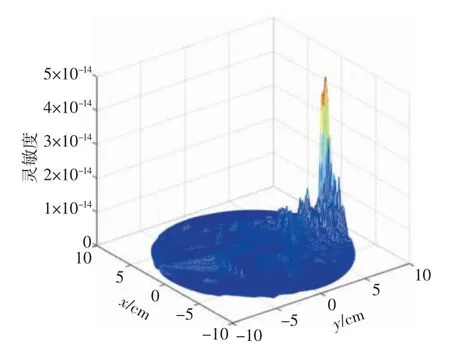
图1 传统激励场下的MIT 系统灵敏度场

（1）灵敏度场分布普遍不均匀、不平缓，各种灵敏度场之间的差异主要取决于激励线圈和检测线圈位置的不同，即特定的“投影”方向[7]。

（2）激励线圈和检测线圈附近灵敏度较高，而处在激励线圈和检测线圈之外的部分灵敏度场数值则较小，且个别点的灵敏度存在负值。

（3）无论是采用哪种激励检测方向，被测圆域的中心处灵敏度值都相对较小。

根据MIT 系统灵敏度场的分布并结合灵敏度场的计算表达式分析，造成灵敏度场中心灵敏度低、灵敏度分布不均匀的原因在于系统激励产生的激励磁场分布不均匀且在被测体中心处的激励磁场强度较低。目前针对被测体中心磁感应信号弱这一问题所设计的均匀场系统大多采用增强整体磁场强度的方法来增加成像区域的激励能量[12]。该方法虽然能提高被测体中心处的信号强度，但是整个被成像区域的磁感应信号全部增强了，故整个磁场的分布没有太大变化，并不能解决灵敏度场分布不均匀这一问题。

本文依据MIT 基本原理与灵敏度的表达式，提出了系统改进方案，并采用基于亥姆霍兹线圈产生的均匀磁场作为激励，从而达到提高被测体中心处磁场强度目的的同时保证整个灵敏度场的均匀分布，以确保磁感应检测结果的准确度。

2 均匀磁场设计

2.1 均匀磁场亥姆霍兹线圈对设计

亥姆霍兹线圈是一种制造小范围均匀磁场的器件，由一对完全相同的半径为R 的圆形线圈组成[13]，2 个线圈同轴放置，距离为H。2 个线圈载有同向电流I，当满足R=H 时，可以使得2 个线圈中心位置O（即原点）的磁场的不均匀程度极小化，达到建立均匀磁场的目的。

考虑到均匀磁场需完全覆盖被测体位置，对线圈大小、匝数、激励电流进行调整，采用半径为30 cm、线径为0.4 mm、匝数为50 匝的线圈构成亥姆霍兹线圈，线圈绕制后的横截面积为0.09 m2，对亥姆霍兹线圈通以频率为10 MHz 的1 A 电流。由于线圈的宽度问题，线圈之间的距离需要进行调整。对线圈摆放位置进行对比，取L（L 为单个线圈到系统中心点的距离，即L=H/2）的范围为13～18 cm，对线圈放置位置进行步长为0.1 cm 的扫描，并提取其中心轴线上的磁场强度。图2 展示了L 在16.4～17.6 cm 范围内的提取结果。

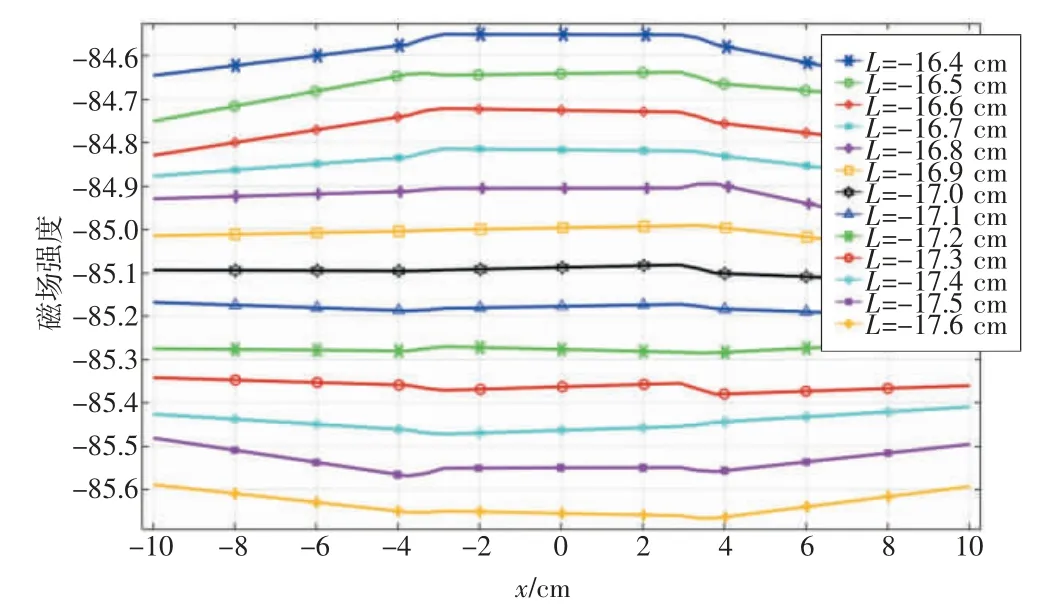
图2 亥姆霍兹线圈中心轴线磁场强度

通过分析得出在线圈放置于±17 cm 位置处时，线圈产生的磁场均匀度最高，所以在仿真中将亥姆霍兹的线圈放置于±17 cm 位置处。建立亥姆霍兹线圈仿真模型，并对其产生的磁场进行计算，仿真结果如图3 所示。

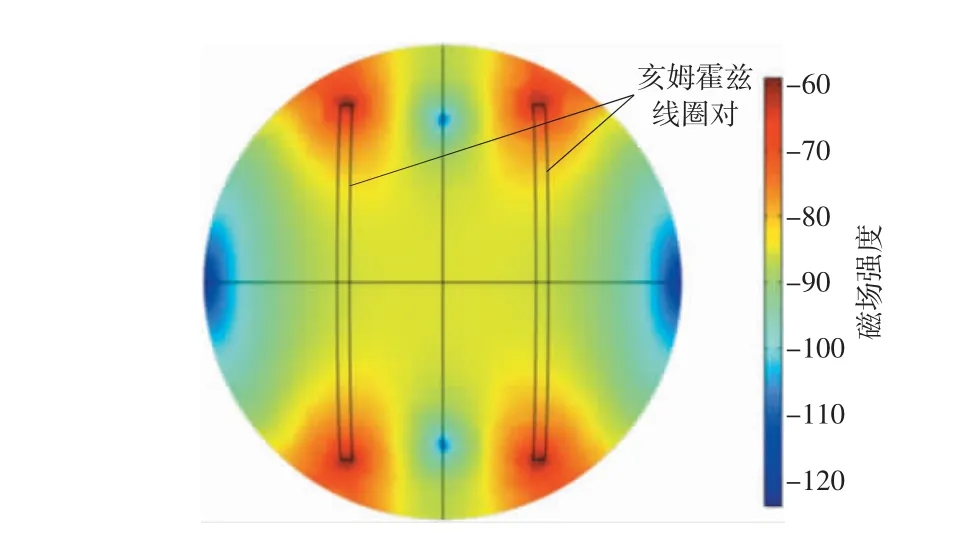
图3 亥姆霍兹线圈激励仿真结果

由图3 可以看出，在亥姆霍兹线圈中心处的磁场分布非常均匀。为探究亥姆霍兹线圈产生的均匀磁场区域能否覆盖整个成像区域，取半径为10 cm 的中心圆形区域计算该区域的磁场均匀性。通过计算得出，在成像区域内亥姆霍兹线圈产生的磁场变化小于3%，磁场分布均匀，符合系统改进的要求。

2.2 磁场驱动的设计

MIT 是利用生物组织的电特性（导纳、阻抗、介电常数等）及其不同的生理和病理变化，对生物体进行无损检测和评价。但是生物组织的电导率很低，提取反映生物组织电特性的信号很困难。除了优化传感器的结构参数，提高传感器检测精度的另一有效方法是增加励磁线圈的电流[14]。增加被测物体的生物组织涡流，有利于检测信号的提取，但是电磁场的作用会增加癌变的可能性。因此，有必要合理地选择激励电流的大小，使检测信号不会淹没在强背景信号中，同时不会对人体造成伤害。本文选择激励电流大小为1 A。

在磁感应系统中，当激励信号的频率非常接近谐振频率时，系统才有较高的检测准确性。同时，磁感应信号的强度与激励信号的频率基本呈线性关系，所以本文选择10 MHz 作为激励源频率。

2.3 被测体磁场分析

将传统MIT 系统与基于亥姆霍兹线圈为激励的均匀场系统中的被测体处的磁场强度进行对比，评估均匀场MIT 系统的优劣性。导入传统MIT 系统与均匀场MIT 系统模型计算出磁场强度B，并将两系统的仿真磁场强度结果进行色彩归一化处理，结果如图4 所示。

从图4 可以看出，在同样的激励下，亥姆霍兹线圈作为激励线圈产生的磁场强度较传统圆形线圈幅值更大，且在被测体内部的磁场强度也更高。计算成像区域中心处的磁场强度均值并加以比较，得出均匀场MIT 系统在中心区域磁场强度提升了近20.1倍。根据前文所述，如果只增强整个磁场强度，并不能解决系统灵敏度场分布不均匀的情况，为研究被测体内部磁场分布的均匀性，同时测量两系统在中心轴线上的磁场强度分布并进行比较，结果如图5所示。

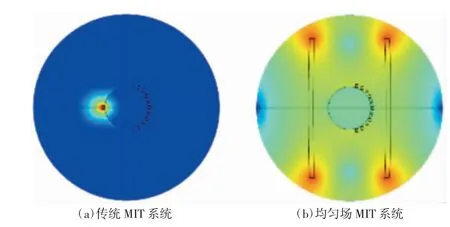
图4 传统MIT 系统与均匀场MIT 系统仿真结果对比

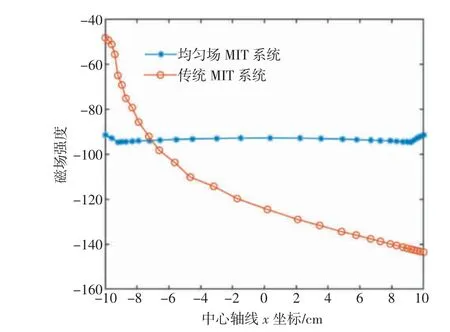
图5 传统MIT 系统和均匀场MIT 系统中心轴线磁场强度分布

由图5 可以看出，在成像深层区域（x 坐标为0处附近）均匀场MIT 系统产生的磁场强度较传统MIT 系统产生的磁场强度更高，且在整个被测体区域，均匀场MIT 系统的磁场强度分布明显更为均匀。与传统MIT 系统相比，均匀场MIT 系统在被成像区域处的磁场强度、磁场均匀度均表现出更为优越的性能。

3 均匀场MIT 系统设计

MIT 系统由激励线圈、检测线圈和后置电路3个部分构成。当高频交变激励电流通过激励线圈时，会产生交变磁场，且频率与交变电流相同[15]。常见的MIT 系统框图如图6 所示。当激励磁场通过被测体时，磁场的相位会发生偏移，相位的偏移量与被测体的电导率分布直接相关。检测线圈依据电磁感应定律，会因偏移后的磁场产生感应电流，通过后置电路对检测线圈电流进行分析可得作用在被测体后的磁场的相位。通过对相位数据进行重建可得出被测体的电导率分布图像。

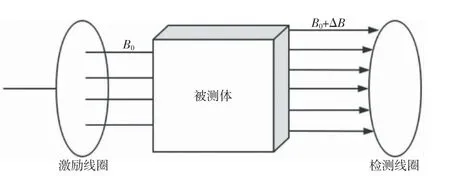
图6 常见的MIT 系统框图

为避免线圈出现串扰问题，本文设计的检测线圈采用扇形阵列结构。由于均匀场MIT 系统的磁力线较传统MIT 系统发生了变化，所以对检测线圈放置角度进行分析。

当激励场处于均匀状态时，磁场磁力线可视为沿亥姆霍兹线圈对轴线平行，如图7 所示。为保证检测线圈的磁感应效率，设计所有检测线圈垂直亥姆霍兹线圈对轴线放置。另外，当检测线圈位于中心轴线90°位置，即位于成像区域正上方时，穿过其所在位置的磁力线未经过成像区域，检测数据并未包含有效的被测体电导率信息，所以本文设计的检测阵列为11 个检测线圈在激励线圈轴线方向-75°～75°范围均匀且垂直于中心轴线放置。检测线圈与激励线圈同步进行步长为2°的旋转扫描。检测线圈采用半径为1.5 cm、匝数为10 的铁磁线圈。

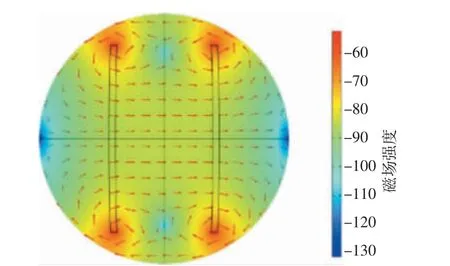
图7 均匀场磁力线分布

本文采用亥姆霍兹线圈作为激励线圈，设计均匀场MIT 系统，建立3 层球体作为被测体。将亥姆霍兹线圈对置于被测体两侧通以相同的同向激励电流。仿真模型如图8 所示。

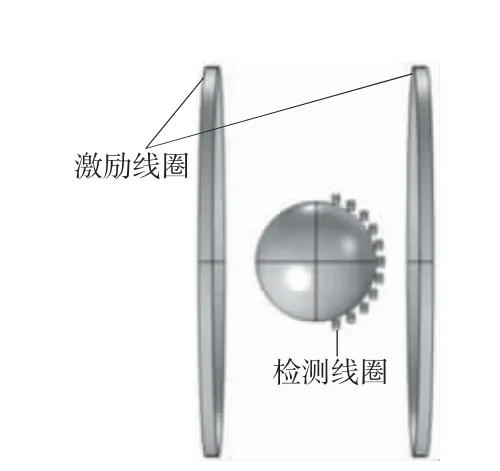
图8 均匀场MIT 系统仿真模型

4 仿真实验评估

4.1 磁感应信号分析

本文旨在通过对MIT 系统的改进提升磁感应信号。为保证在提升信号的同时能够提升系统对不同位置处干扰目标进行检测所得信号的差异性，建立检测模型，分析检测所得信号。首先，在建立好的均匀场MIT 系统中加入半径为1.5 cm 的球形扰动目标，分别将扰动目标依次放置在成像区域内的中心位置和以系统中心为原点的上、下、右各4 cm 处，如图9 所示。然后，进行仿真，提取检测线圈所得数据。其中，成像区域为半径9.2 cm 的圆形，背景电导率为0.1 S/m，扰动电导率为0.6 S/m。

图9 干扰目标示意图

在检测模型中提取加入干扰目标后产生的二次磁场，由于亥姆霍兹作为激励线圈产生的主磁场在成像区域内各位置处的方向一致，所以在检测线圈位置处提取复合磁场的y 分量即可提取出由检测目标感生的二次磁场，将加入干扰目标前后提取出的数据进行差值处理，所得数据即为扰动目标所感生的磁感应信号，同时在传统MIT 系统中进行相同处理，并提取副磁场强度数据。

由图10 可以看出，当干扰目标加入成像区域的中心与右侧时，检测线圈所接收到的磁感应信号皆为对称信号，但是数值与变化率有明显区别。当干扰目标加入成像区域的上侧与下侧时，磁感应信号的对称性被破坏，且与干扰目标位置相近的检测线圈接收到的磁感应信号变化较大。同时对比传统MIT 系统各位置加入扰动目标后感生的磁感应信号（如图11 所示），均匀场MIT 系统接收的磁感应信号在强度和对干扰目标位置的敏感度方面均远优于传统MIT 系统。

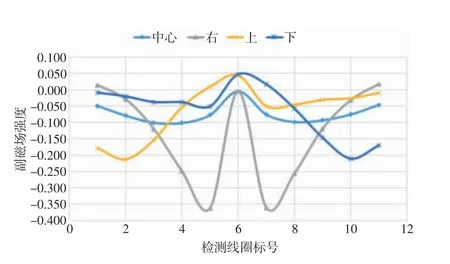
图10 均匀场MIT 系统各位置加入扰动目标感生的磁感应信号

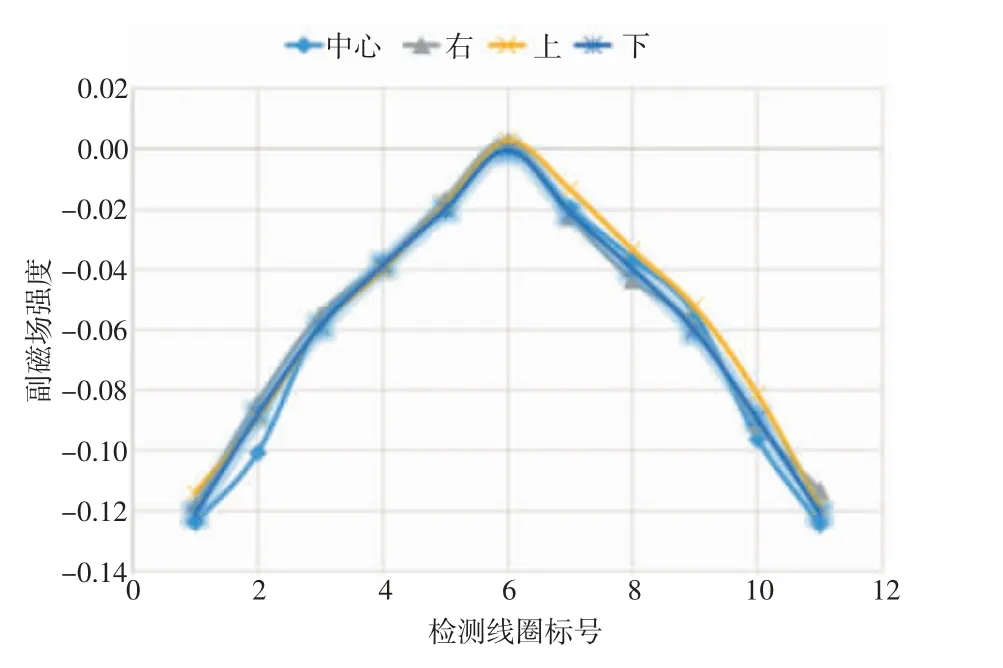
图11 传统MIT 系统各位置加入扰动目标感生的磁感应信号

4.2 灵敏度分析

本文从MIT 系统的灵敏度场出发，分析其特性与原因，提出系统改进思路，为保证改进后的系统能满足提高成像区域处的检测灵敏度的要求，对传统MIT 系统和均匀场MIT 系统的灵敏度场进行对比分析。

4.2.1 灵敏度场求解

计算传统MIT 系统和均匀场MIT 系统中的6号检测线圈与激励线圈对的灵敏度场，将模型中的成像区域剖分，形成6625 个单元点，分别计算当激励线圈与6 号检测线圈通以单位激励时成像区域处的电场分布，然后提取相应数据。根据公式（1）～（3）求解两系统的灵敏度场，得到的结果如图12 所示。

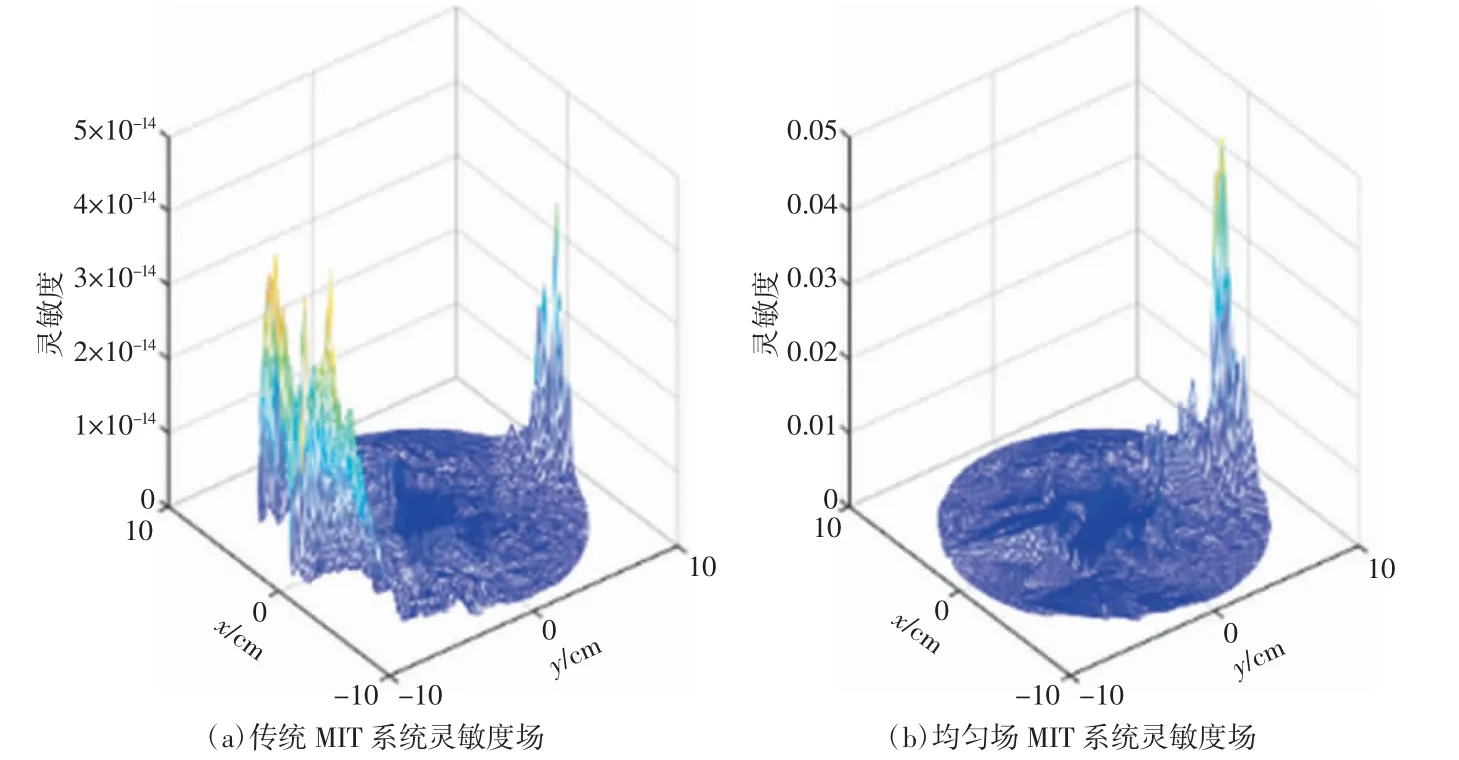
图12 传统MIT 系统与均匀场MIT 系统灵敏度场对比图

4.2.2 灵敏度对比分析

分析灵敏度场的分布均匀度特性，一般采用灵敏度数据计算标准差的方式来进行，但由于2 组数据的数值差别太大，不在同一数量级上，为了消除数量级的影响，采取通过变异系数（变异系数=标准偏差/平均值）来评价灵敏度场的均匀度。变异系数越小，表明数据的离散程度越低，即灵敏度场分布越均匀。

在成像区域内，以成像中心为圆心、R 为半径画圆，取R=9.2 cm 时为整个成像区域、R=4 cm 时为中心区域。计算整个被测区域中的所有点的灵敏度值，并计算2 个系统各自的变异系数，同时取中心区域（R≤4 cm）中的灵敏度变异系数来对比灵敏度场的均匀度，结果见表1。

表1 传统MIT 系统与均匀场MIT 系统灵敏度变异系数对比

为比较两系统中心磁感应信号的感应情况，取被测体中心处的半径为1 cm 的圆形区域的灵敏度进行对比，均匀场MIT 系统、传统MIT 系统的中心灵敏度均值分别为1.03×10-1、1.29×10-3，两系统中心灵敏度对比图如图13 所示。从两系统中心灵敏度对比的结果可以明显看出，均匀场MIT 系统的灵敏度数值较传统MIT 系统提高了近2 个数量级。

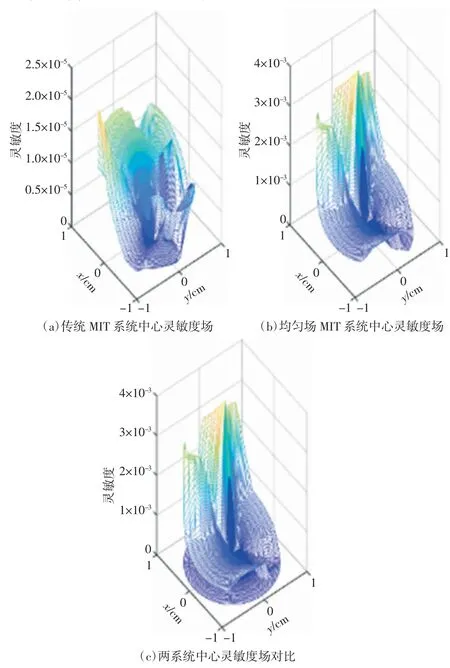
图13 传统MIT 系统与均匀场MIT 系统中心灵敏度场对比图

通过计算结果可以看出，均匀场MIT 系统无论在整体区域还是在中心区域，其灵敏度均匀性均高于传统的MIT 系统。同时，在成像区域深层，均匀场MIT 系统的灵敏度要远高于传统的MIT 系统。在响应均匀度与响应强度方面，均匀场MIT 系统均表现出优越性。

5 结语

本文通过对MIT 系统的灵敏度进行分析，总结出了传统MIT 系统磁感应信号弱的原因。然后设计了一种均匀场MIT 系统，采用亥姆霍兹线圈替代传统圆形线圈作为激励，通过对亥姆霍兹线圈进行有限元仿真并分析得出了适于本文所要求的结构与位置参数。从磁场、磁感应信号和灵敏度3 个方面对本文设计的均匀场MIT 系统进行分析评估，得出该系统在整个成像区域尤其在成像中心处产生的磁场能量更强。对不同位置变化所产生的扰动目标进行检测，本文设计的均匀场MIT 系统得到的磁感应信号更强且对位置变化所产生的差异性更加明显。均匀场MIT 系统在整个成像区域的灵敏度较传统MIT系统有较大程度提高。本文完成了均匀场MIT 系统的仿真实验与分析，确立了整个系统的参数与可行性，但未搭建硬件系统检测平台。今后将在现有的工作基础上建立系统检测平台、颅脑琼脂仿真模型，探究采用亥姆霍兹激励线圈的MIT 系统对颅脑组织琼脂仿真模型的检测实验效果，并对系统进行进一步优化。