基于光谱指数的晋西黄土区土壤黏粒含量估测

孙瑞鹏，丁皓希，毕如田，邓永鹏，朱洪芬

（山西农业大学 资源环境学院，山西 太谷 030801）

土壤黏粒含量是土壤最基本的物理性质之一， 对土壤的水肥气热等各种性质均有影响，土壤质地的实验室测定方法主要有沉降法和激光粒度仪法，其中，激光粒度仪法出现时间短，相比沉降法所测定的黏粒含量偏低，测定过程比较费时且成本较高[1-5]。目前，已有学者采用高光谱技术预测土壤黏粒含量，常用光谱变换来提高土壤黏粒含量的预测能力。王德彩等[6]引入正交信号校正（Orthogonal signal correction，OSC）处理后的光谱对土壤黏粒含量进行预测，结果表明，预测结果OSC处理高于原始光谱和微分处理，且OSC处理能消除不相关因素的影响。张雅梅等[7]选用7种光谱变换形式对土壤黏粒含量进行预测，结果表明，原始光谱的对数为最佳的光谱变换形式，且对土壤黏粒含量的预测能力最佳。虽然使用预处理光谱能够预测土壤黏粒含量，但这样只是通过多波段信息来建立预测模型，预测所用光谱信息比较单一，并未结合较多的光谱特征信息。

在基于高光谱的预测模型方面，近年来较多采用非线性模型用于土壤属性的预测研究。张娜等[8]采用一元线性回归、逐步多元回归和神经网络预测土壤砂粒和粉粒含量，结果表明，神经网络的预测效果更好。相比线性模型，采用非线性模型会提高土壤质地的预测精度，由于非线性模型的容错性强且有较强的鲁棒性，对预测模型起到了显著的优化效果。另外，还有不少研究者通过构建光谱指数以提高其预测能力，并筛选出各种土壤光谱特征指数解释其对光谱曲线的影响。例如，张娟娟等[9]构建差值光谱指数DI（CR1883，CR2065）较好地估测了土壤有机质、全氮和速效氮3种土壤养分。赵明松等[10]构建差值指数、比值指数和归一化指数，结合弓曲差较好地实现了土壤有机质的预测。尼加提·卡斯木等[11]对光谱指数进一步优化处理，结果表明，土壤光谱指数能更好地预测土壤有机质。还有相关学者采用不同光谱指数对土壤盐分、土壤电导率等土壤属性进行预测研究得出，模型预测良好[12-13]。以上研究表明，土壤光谱指数可以较好地预测土壤的基本属性。

黄土高原土壤颗粒组成主要以粉粒和砂粒为主，二者含量占颗粒总量的50%以上[14]，土壤黏粒含量较低，抗蚀性较弱[15-16]。而晋西黄土区是水土侵蚀较严重的区域，土壤黏粒含量是评价水土侵蚀的重要因子，较低的土壤黏粒含量为其光谱预测带来了挑战。

本试验以位于晋西黄土区的临汾市大宁县为研究区，基于土壤高光谱预处理数据构建光谱指数模型，通过相关性分析筛选出最优土壤黏粒光谱指数，并采用多种预测模型构建土壤黏粒含量预测的最优组合形式，旨在为晋西黄土区土壤黏粒含量的快速预测提供方法。

1 材料和方法

1.1 研究区概况

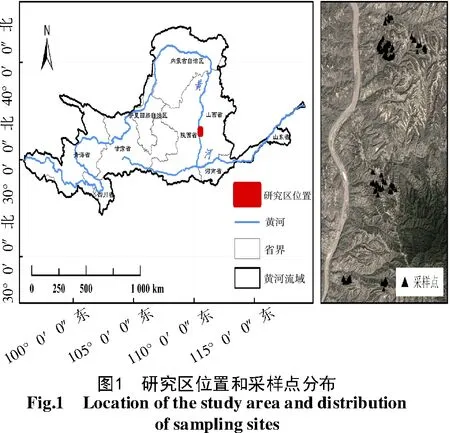
山西省临汾市大宁县位于黄河中游，晋西吕梁山南端，位置36°16′～36°36′N，110°28′～111°01′E。地形南北高、中间低，东部高、西部低，海拔最低481 m，最高1 740 m，属暖温带大陆性气候，年均气温11.1℃，年均降水量536.9 mm。根据国家土壤信息服务平台（http://www.soilinfo.cn/map/）中国1∶400万土壤类型图可知，区域内土壤类型主要有黄绵土和褐土两大类。

1.2 土壤样品采集与质地测定

土样采集时间为2020年11月，采样深度为20 cm，所采土样质量约1 kg，记录采样点的位置信息，共采集土样192个（图1）。土样带回实验室内自然风干后，将土样分成2份，一份原土过2 mm筛用于土壤质地测定；另一份研磨后过2 mm筛用于土壤高光谱测定。

土壤粒径数据使用激光粒度仪Mastersizer 3000进行测定，测定粒径范围为0.02～2 000μm，测定前采用H2O2-HCl-（NaPO3）6法对土样进行预处理：首先将2～5 g小于2 mm的土样放入高型烧杯中，缓慢少量逐次加入30%的H2O2，直至没有气泡产生；然后多次滴入10%的HCl，直至碳酸盐完全去除；最后多次使用蒸馏水洗至中性后，移除上清液并加入浓度为0.1 mol/L的（NaPO3）6分散剂，将样品放到超声波振荡器中10 min，待样品分散后用于测定[4，17-19]。根据美国农部制土壤质地分类法将测定所得土壤粒径划分为：黏粒（＜0.002 mm）、粉粒（0.002～0.050 mm）、砂粒（0.05～2.00 mm）。本研究选用土壤黏粒含量进行分析。

1.3 土壤光谱测定

土壤光谱使用ASD Field Spec 4 Std-Res地物光谱仪进行测定，波长范围为300～2 500 nm，在黑暗的实验室环境下进行。将土样装入深2 cm的培养皿中并压实，光纤探头采用10°镜头，保持与土样垂直距离15 cm，光源天顶角为30°，距离土样50 cm；每个土样旋转重复测定5次，以这5条光谱曲线的平均值作为土样的光谱数据。由于数据在350～400 nm和2 450～2 500 nm这2段光谱波段的信噪比大，在计算分析中剔除，然后对400～2 450 nm光谱数据进行Savitzky-Golay滤波9点平滑处理后并按5 nm间隔进行重新采样，共得到411个波段作为光谱分析数据。

1.4 光谱变换与光谱指数构建

首先将原光谱反射率（Reflectance，R）进行3种变换：倒数变换（Inverse of R，IR）、倒数的对数变换（Logarithm of 1/R，LGIR）、倒数的一阶微分变换（First derivative of 1/R，FDIR）；然后将以上4种形式的光谱曲线通过光谱指数两两组合，主要有差值光谱指数（Difference spectral index，DSI）、比值光谱指数（Ratio spectral index，RSI）和归一化光谱指数（Normalized difference spectral index，NDSI）；最后计算土壤黏粒含量，并将其与各个光谱指数进行相关性分析，在相关性等势图中用区域极值的方法，选择区域内相关性较高的光谱指数建立模型。

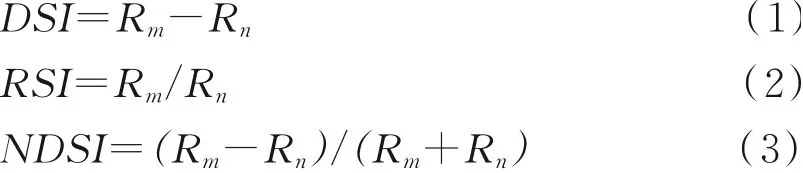
式中，Rm和Rn分别代表m和n波段的土壤光谱反射率（m＞n）。

1.5 建立模型与精度评价

采用土壤黏粒含量和选取的土壤光谱指数建立模型，模型包括多元线性回归（Multivariable linear regression，MLR）、偏最小二乘回归（Partial least squares regression，PLSR）、反向传播神经网络（Back propagation neural networks，BPNN）；对土壤黏粒含量依次排序，按照3∶1将全部样本分为建模集和验证集，分别为144个和48个样本；采用决定系数（Coefficients of determination，R2）、均方根误差（Root mean squares error，RMSE）、相对分析误差（Relative prediction deviation，RPD）3个参数对模型精度进行评价。

式中，yi为样本i实测值，y^i为样本i预测值，yˉ为样本实测平均值，n为样本数，SD为样本实测值的标准差。

R2值越大、RMSE值越小，表示模型精度越高。本研究将RPD值分为6类：RPD＜1.0表示模型预测非常差，不推荐使用；RPD在1.0～1.4表示模型预测比较差，只能用于区分高值和低值；RPD在1.4～1.8表示模型可用于预测；RPD在1.8～2.0表示模型预测良好；RPD在2.0～2.5表示定量模型预测非常好；RPD＞2.5表示模型预测极好[20-21]。

1.6 数据分析

光谱数据预处理使用View Spec Pro 6.2软件完成；光谱变换、光谱指数、相关性计算和模型计算均使用Matlab 2019b软件完成。

2 结果与分析

2.1 不同土壤黏粒含量的光谱特征分析

根据美国农部制土壤质地分类法[22]，192个土壤样本中有188个为粉壤土，3个为粉土，1个为砂壤土，其中，土壤黏粒含量最小值为4.03%，最大值为17.83%，平均为8.00%；按照土壤黏粒含量从小到 大 排 序 为1～17、18～64、65～120、121～165、166～184、185～192个 土 样 的 平 均 值 分 别 是5.00%、6.32%、7.50%、8.89%、10.85%、16.02%，共6组，计算每一组土样的光谱平均值如图2-A所示。土壤黏粒含量对土壤光谱的影响主要体现在近红外波段；随着土壤黏粒含量的增加，1 450 nm和1 950 nm处的水分吸收明显，即光谱吸收谷越深（图2-B、C），土壤黏粒含量越高，光谱曲线在近红外波段反射率越低，且光谱差异较大，反之，光谱曲线在可见光波段差异较小。AL-ABBAS等[23]在对土壤质地与光谱的研究中指出，土壤黏粒含量与其光谱反射率呈负相关，土壤黏粒含量越高反射率越低，与本研究结果一致。

2.2 土壤黏粒含量与光谱指数的关系

通过分析土壤黏粒含量与原始光谱（R）、倒数（IR）、倒数的对数（LGIR）及倒数的一阶微分（FDIR）的相关性可知（图3），相关系数较高值分别为-0.28、0.27、0.28、-0.61，经IR和LGIR变换后的相关系数并未提升，而经FDIR变换后其相关性明显提升，相关性较高的波段主要位于1 450、1 950、2 200 nm光谱吸收谷两侧。

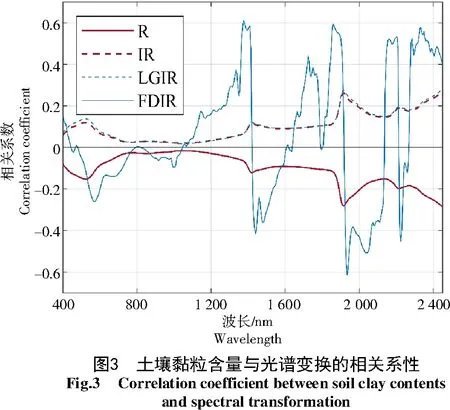
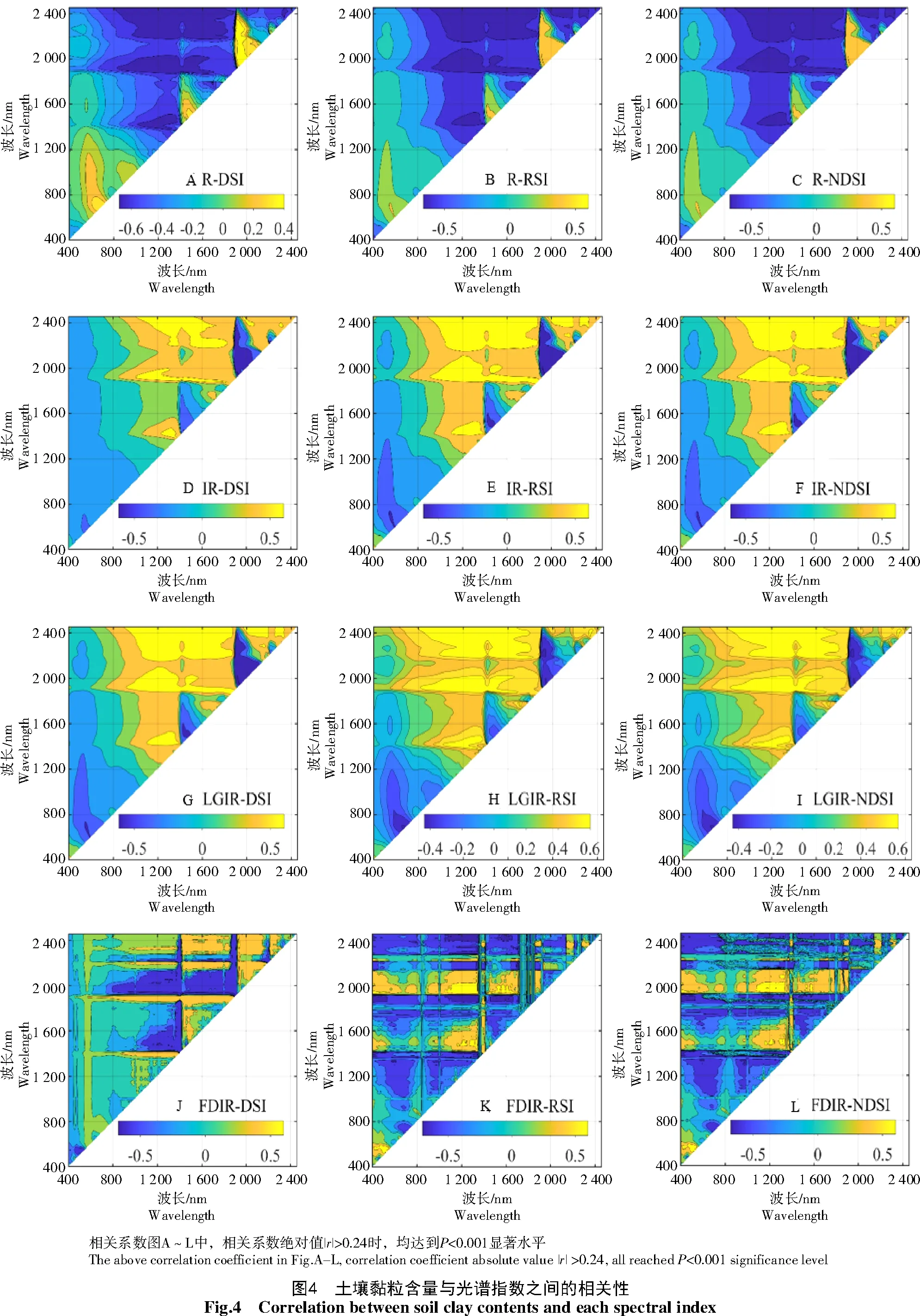
图4为光谱变换对应的差值（DSI）、比值（RSI）及归一化（NDSI）光谱指数与土壤黏粒含量的相关关系情况。从图4可以看出，在同一种光谱变换形式下，DSI、RSI和NDSI这3种指数的正负相关性区域相近，其中，DSI相关性图与RSI和NDSI存在较大差异，而RSI和NDSI相关性区域基本保持一致；在同一种光谱指数下，IR和LGIR这2种变换正负相关性区域比较吻合，且二者与原始光谱的正负相关性区域正好相反。总体来看，相关性区域相对集中，相关性最高的区域分布在波段1 450、1 950、2 200 nm吸收谷的两侧，波段组合为（2 245，1 515）、（2 425，1 155）、（2 440，1 155）、（1 900，1 460）、（2 240，1 515），相关系数绝对值在0.66～0.70；反之，FDIR变换对应的相关性区域比较分散，DSI、RSI、NDSI对应的显著相关性最高波段组合分别为（1 930，1 420）、（2 420，1 570）、（1 940，400），相关系数分别为-0.67、-0.70、0.69；相较于单波段，波段两两组合与土壤黏粒含量的相关性均有提升。从土壤黏粒含量与光谱指数的相关性来看，光谱指数RSI最优，NDSI和DSI表现次之（表1）。

由于相关系数区域比较集中，为减少构建模型时自变量之间共线性的影响，对相关系数图进行求极值，然后在每种光谱指数中筛选出相关系数极值绝对值最大的5个土壤光谱指数。基于以上最优土壤光谱指数，采用多元线性回归方法构建土壤黏粒含量的预测模型，建模结果如表1所示，12种形式的建模集R2在0.47～0.57，RMSE在1.42～1.59，对应大小与每一类型相关系数绝对值大小有关，波段组合与土壤黏粒含量相关性越高，建模精度越高；验证集R2在0.45～0.61，RMSE在1.42～1.71，RPD在1.30～1.57，除FDIR-DSI和FDIR-NDSI之外，其余10种形式的RPD均大于1.4，能够粗略地估测土壤黏粒含量；其中预测精度最高的是FDIR-RSI，建模集的R2和RMSE分别为0.57、1.42，验证集的R2、RMSE和RPD分别为0.61、1.42、1.57，其 次 分 别 为R-DSI、R-NDSI、IRNDSI、LGIR-DSI。

表1 各光谱指数与土壤黏粒含量的关系Tab.1 Relationship between each spectral index and soil clay contents

2.3 基于PLSR和BPNN的土壤黏粒含量估测

与MLR采取同样的光谱指数选取方法，通过极值结果选取相关系数绝对值最大的47个光谱指数，用于PLSR和BPNN预测，模型结果如表2所示，PLSR模型建模集R2和RMSE分别在0.60～0.67、1.25～1.38，验证集R2、RMSE和RPD分别在0.50～0.57、1.46～1.56、1.42～1.52，其中，RPD均大于1.4，预测精度高的是FDIR-RSI，建模集的R2和RMSE分别为0.63、1.32，验证集的R2、RMSE和RPD分别为0.57、1.54、1.52，预测精度其次依次为R-DSI和LGIR-RSI；BPNN模型建模集R2和RMSE分别在0.64～0.70、1.21～1.32，验证集R2、RMSE和RPD分别在0.55～0.74、1.13～1.49、1.50～1.96，同样RPD均大于1.4，预测精度高的是LGIRNDSI，建模集的R2和RMSE分别为0.64、1.32，验证集的R2、RMSE和RPD分别为0.74、1.13、1.96，预测精度其次为LGIR-RSI、LGIR-DSI和FDIRRSI。总体来看，在LGIR变换下3种光谱指数构建的BPNN模型精度都比较好，整体比较DSI、RSI和NDSI对应的模型精度，RSI和NDSI优于DSI。比较PLSR、BPNN模型建模集和验证集的R2和RMSE可知，BPNN表现最优，其次为PLSR。

表2 基于光谱指数的土壤黏粒含量估测结果Tab.2 Estimation of soil clay contents based on spectral indexes

图5是模型预测效果，对比实测值与预测值分布，存在低值高估和高值低估的现象；BPNN预测结果更接近1∶1线，预测结果有所改善，非线性模型BPNN用于预测土壤黏粒含量比传统线性模型表现更好。

3 结论与讨论

已有研究采用光谱指数预测其土壤属性，模型预测使用光谱范围主要为近红外光谱区域。同样，本研究结果表明，土壤黏粒含量与光谱指数显著相关性的区域主要分布在近红外区域，主要为（2 245，1 515）、（2 425，1 155）、（2 440，1 155）、（1 900，1 460）、（2 240，1 515）等相邻区域，这与已有光谱指数预测土壤属性结果一致。郭鹏等[13]通过构建光谱指数预测土壤盐分，发现相关系数高的光谱范围为1 430～1 862、1 934～2 150 nm，筛选出敏感亮度指数（1 750，1 620）,并采用随机森林（Random forest，RF）建立预测模型，且模型精度较高。张娟娟等[9]构建差值光谱指数DI（CR1883，CR2065）用于估测土壤有机质、全氮和速效氮3种土壤养分，结果发现均有较好的效果。

在光谱变量选取方面，本研究采用光谱指数结构固定、光谱波段随机组合的方式构建光谱指数，并使用与土壤黏粒含量的相关性筛选局部区域的最优光谱指数，以提升土壤黏粒含量的预测精度。已有研究常采用相关性、主成分变换等方法减少输入变量，例如，杨莎等[24]使用相关性分析筛选敏感波段用于预测土壤有机质。白燕英等[25]通过土壤黏粒含量与光谱的相关性选择波段用于建立预测模型，精度超过85%。乔天等[26]采用遗传算法选择变量并结合偏最小二乘回归建立土壤质地模型，结果减少了光谱变量，也提高了预测精度。王德彩等[27]采用光谱主成分为变量使用BP神经网络预测土壤黏粒含量，实现了高效预测。而本研究使用光谱指数一方面避免了筛选出相邻光谱存在的光谱互相关，提高了预测模型的稳健性；另一方面光谱指数能够更多选取到不同的光谱波段，涉及的光谱信息更多。

在土壤光谱预测方面，较多使用PLSR模型预测土壤属性。本研究同时使用PLSR和BPNN对土壤黏粒含量进行预测，结果表明，BPNN预测能力更强更稳定。同样，郭云开等[28]使用BPNN预测土壤Cu含量，结果表明，相比单元线性回归模型，BPNN具有良好的拟合优度和预测能力。虽然本研究使用光谱指数预测了晋西黄土区的土壤黏粒含量，可以为遥感估测土壤黏粒含量提供技术支持，但相比较大尺度范围遥感估测，研究区域还较小，土壤类型较单一，导致光谱指数预测土壤黏粒含量模型适用性较差，所以该方法用于不同区域还有待进一步探究。

本试验基于光谱指数的晋西黄土区的土壤黏粒含量估测研究结果显示，土壤黏粒含量对光谱曲线的影响主要为近红外波段，原始光谱与土壤黏粒含量呈负相关，土壤黏粒含量越高，土壤光谱反射率越低；通过构建光谱指数可以提高与土壤黏粒含量之间的相关性，是提高预测土壤黏粒含量的方法之一；基于LGIR-NDSI-BPNN的预测效果最好，验证集R2和RPD分别为0.74和1.96，能够有效地预测晋西黄土区的土壤黏粒含量。为了提高光谱指数预测土壤黏粒含量的精度，将针对不同土壤类型、多种光谱指数探究最佳的光谱预测指数和方法。