融合图注意力的多特征链接预测算法
张雁操,赵宇海,史 岚
东北大学 计算机科学与工程学院,沈阳110169
链接预测是复杂网络研究工作中重要研究方向之一,是指通过已知的部分网络结构预测网络中两个节点是否存在链接。这些链接可能是缺失的或未被观察到的,也可能是未来网络演变过程中可能产生的。因此链接预测可以帮助人们更好地补全网络或理解网络结构生成及演化的机制。
作为一个典型的交叉学科,链接预测已经成为数据挖掘领域重要的研究方向之一,其应用场景涉及许多领域。例如,在生物领域,可用于预测蛋白质之间的相互作用,在Yeast网络中,大部分细胞间相互作用尚不为人知;在社交领域,可用于预测社交活动的产生或消失;在交通领域,可以用于交通线路规划、城市道路规划;在推荐领域,可以进行商品推荐、好友推荐等。
目前有一类简单的链接预测方法是基于相似函数的链接预测,也称作启发式方法。该类方法假设:节点倾向于与其相似的节点形成链接。通过定义相似性函数计算两个节点的相似性,然后将节点对的相似性得分按递减顺序排列,位于排序顶部的链接更有可能为丢失链接或者未来可能相连的链接。
基于计算相似性所需节点的距离可将启发式方法分为三种:一阶、二阶及高阶。一阶启发式仅仅涉及两个目标链接节点的一跳邻居节点,例如共同邻居(common neighbors,CN)、Jaccard 指数(JA)、优先连接指数(preferential attachment index,PA)等。二阶启发式是通过目标链接节点的两跳邻居计算相似性的,例如Adamic-Adar 指数(AA)、资源分配指数(resource allocation index,RA)等。还有需要更大范围甚至是整个网络的相似性度量方法,称为高阶启发式,例如PageRank(PR)、Katz指数(Katz index,KI)、SimRank(SR)、随机游走(random walks,RW)等。尽管这类方法实践效果良好,但是对于链接的存在性有很强的人为假设。对于不同类型的数据集,相似性函数往往有着不同的定义。例如,CN 假设若两节点有更多的共同邻居,则它们更有可能相连,这种假设在社交网络中可能是正确的,但是在蛋白质交互网络(protein-protein interaction networks,PPI)中被证明是无效的;JA 通过计算两个节点的完整邻居集合中共同邻居的比例度量节点相似性;PA 假设两个节点之间形成链接的概率随着节点度的增加而增加。
另一类近年来被用于链接预测任务的是节点嵌入算法。本文按节点嵌入算法获取向量表示的过程将其分为两类:第一类是通过保留节点的局部邻域信息,用于特征提取、节点分类、链接预测等任务的算法,例如DeepWalk、LINE、N2V(node2vec)等。第二类算法从全局角度挖掘每个节点的潜在特征信息,通过保留节点的结构特征相似性、社区信息、全局排序信息等生成节点嵌入向量,例如struc2vec、M-NMF(modularized nonnegative matrix factorization)、NECS(network embedding with community structural information)、PRUNE(proximity and ranking-preserving unsupervised network embedding)等。
node2vec 节点嵌入算法第一次将链接预测作为下游任务评估算法性能。它从广度优先和深度优先两个角度,使用有偏随机游走最大限度地保留节点的邻域信息,并利用低维向量表示进行链接预测等任务。PRUNE 设计了保留多种特征信息的目标函数,使用孪生神经网络进行无监督学习,将得到的向量表示用于链接预测等任务。另外由网络的同质性原理,同一社区中的节点比不同社区间的节点更相似。M-NMF 和NECS 节点嵌入算法利用矩阵分解,以学习网络的社区结构、保留节点的社区信息为目的,在链接预测任务中取得了良好的效果。但是节点嵌入算法不具有任务特定性——不是针对链接预测任务设计的,被用于特征提取、节点分类、链接预测等多个下游任务,无法捕获对链接预测最有效的信息。
在监督学习中几乎所有的分类器都可以用于链接预测。Lichtenwalter 等人提到将多种分类器用于链接预测,包括决策树、支持向量机、近邻算法、多层感知器、朴素贝叶斯等。Cukierski等人利用随机森林取得了良好的结果。针对启发式方法和节点嵌入算法的缺陷,Zhang 和Chen 首次提出将启发式看作预定义的图启发式特征,利用神经网络学习合适的启发式进行链接预测,并据此提出了WLNM(Weisfeiler-Lehman neural machine)算法。首先提取包含指定节点数的局部子图,然后利用启发于Weisfeiler-Lehman算法提出的PALETTE-WL标记方法获得子图节点标记,最后根据节点标记重构子图邻接矩阵,输入到全连接神经网络中训练。进一步的,Zhang和Chen提出了目前表现最优异的链接预测算法SEAL(learning from subgraphs,embeddings and attributes for link prediction),其中使用的图神经网络DGCNN(deep graph convolutional neural network),具有更好的图特征学习能力,且该算法允许从节点特征中学习,包括DRNL(double-radius node labeling)节点标记和node2vec 节点嵌入特征。但是SEAL 算法具有以下几个问题:
(1)局部性:对于目标链接,该方法通常考虑一跳或两跳局部子图,利用的特征如局部子图的邻接矩阵、局部子图的DRNL 独热编码标记矩阵和node2vec向量表示等。通过神经网络的学习,只能获得低阶启发式特征。
(2)特征无效性:由于目标链接的局部子图可能是不连通的,会导致DRNL 节点标记矩阵具有较强的特征无效性(见1.1 节)。
(3)节点无偏性:在图卷积的过程中,未考虑到不同节点对于链接存在性的影响应该不同,因此对于局部子图中节点信息的聚合过程应该是有偏的(见1.1 节)。
针对SEAL 算法存在的问题,本文提出了融合图注意力的多特征链接预测算法ADNSL(learning from double-radius node labeling,node2vec and struc2vec for link prediction with attention mechanism),主要贡献如下:
(1)针对上述问题(1),提出了一种支持不同类型特征输入的链接预测算法。在局部特征生成模块中,该模型将局部角度的节点嵌入特征输入到图神经网络,学习预定义的启发式特征。在全局特征提取模块中,利用struc2vec 从全局角度提取节点的结构特征,通过重构图上的随机游走生成游走序列,并得到节点嵌入向量,进而提升链接预测性能。
(2)针对上述问题(2)和(3),在局部特征生成模块中提出双向无参注意力图卷积,可以有效弥补特征无效性和节点无偏性(见1.1 节)。
(3)为了降低模型复杂度,在全局特征提取模块中提出了有效的迭代公式,将struc2vec的重构多层图转化为聚合图,在保留结构特征相似性的同时,可以有效减少I/O 时间、内存消耗及磁盘消耗(见1.2 节)。
(4)在八个不同领域公开经典数据集上的实验表明,ADNSL 相比于多个基准模型,ACC 和AUC 值有十分明显的提升。对于平均度较小的数据集NS、Power 和Router,AUC可有10个百分点以上的提升(见2.5 节)。
1 融合图注意力的多特征链接预测算法
本章将详细介绍融合图注意力的多特征链接预测算法模型ADNSL。首先,针对SEAL 算法的局部性,给出了ADNSL 的整体框架图(图1);然后,给出了局部特征生成模块的介绍,针对SEAL 的特征无效性和节点无偏性,给出了双向无参注意力图卷积过程;接着,介绍了全局特征提取模块,并针对重构多层图的特性,提出迭代公式用于生成聚合图。
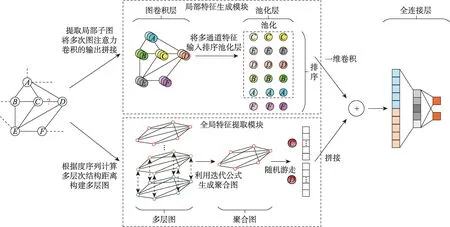
图1 ADNSL 框架Fig.1 Framework of ADNSL
如图1 所示,针对SEAL 算法的局部性,ADNSL框架主体分为两部分,上方为局部特征生成模块,下方为全局特征提取模块。局部特征生成模块利用局部子图的DRNL 节点标记矩阵和node2vec 节点嵌入矩阵作为特征输入,经过多次图注意力卷积得到多感受野的节点特征向量,然后将每一层图卷积的输出结果拼接,并通过排序池化层和一维卷积层,生成局部特征向量,详细过程在图2 中展示。全局特征提取模块使用全局角度struc2vec 方法提取节点嵌入向量,根据多跳度序列计算输入图中节点间的结构距离,并利用结构距离重构原图生成多层图,再利用迭代公式得到聚合图,通过聚合图上的随机游走,提取目标节点的全局特征向量,详细过程在图3 中展示。之后,将两个模块得到的特征表示融合,输入到全连接层预测链接是否存在。整个框架通过有效的多特征融合,可以合理地利用节点嵌入特征,明显地提升链接预测的性能。

图2 局部特征生成模块Fig.2 Local feature generation module
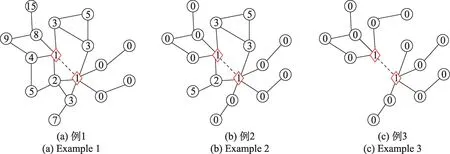
图3 DRNL 特征无效性Fig.3 Ineffectivity of DRNL features
1.1 局部特征生成模块
给定无向无权图=(,),=||,表示节点的集合,表示边的集合,表示节点个数。对图,有邻接矩阵和特征矩阵∈R,其中由DRNL节点标记矩阵和node2vec 节点嵌入矩阵拼接而成。如图2 所示,利用图注意力卷积生成局部特征。
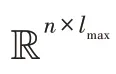
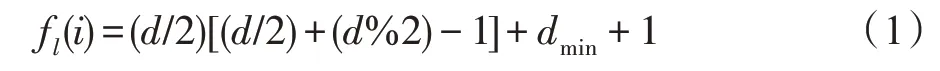
其 中,=d+d,=min(d,d),d=(,) 和d=(,)分别表示节点到目标节点和的距离,(/2)和(%2)分别是除以2 的整数商和余数。特别地,f()=f()=1;若(,)=∞或(,)=∞,则 f()=0 。需要注意的是,在计算距离(,)和(,)时,路径不可通过目标节点和。
式(1)所示的DRNL 节点标记哈希函数具有如下特性:对于局部子图中的任意两个节点、及目标节点、,当(,)+(,)≠(,)+(,)时,(,)+(,)<(,)+(,)⇔f()<f();当(,)+(,)=(,)+(,) 时,(,)(,)<(,)(,)⇔f()<f() 。因此子图中的节点到两个目标节点的距离之和越小,则标记值越小;子图中的节点到两个目标节点的距离之和相等时,距离之积越小,标记值越小。
利用式(1)计算得到的节点标记如图3 所示。菱形节点表示目标节点和。除了标记为0 的节点外,局部子图中标记越小的节点,对于目标链接的存在性越重要。由于计算距离时,路径不可通过目标节点,局部子图中可能含有大量标记为0 的节点。这些节点的标记值对于链接的存在性是无意义的,因此DRNL 节点标记矩阵具有较强的特征无效性。


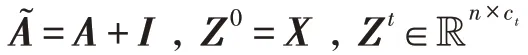
启发于图注意力网络(graph attention networks,GAT),在上述两个问题的基础上,提出融合注意力机制的图卷积过程,可以更加注重有效的特征信息,更好地捕捉节点特征的差异性。对于图中的任意两相邻节点、,在+1 层,有注意力系数:
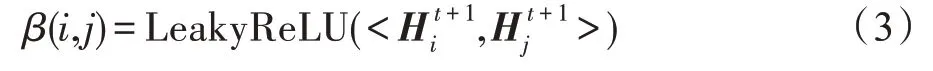
其中,<*,*>表示向量的内积。本文ADNSL 中注意力系数的计算过程与GAT 有两点不同:(1)特征矩阵H是子图中的节点聚合邻居节点的特征后得到的,在计算某两个节点的注意力系数时,除了考虑这两个节点的特征外,还考虑了它们所有邻居节点的特征,这显然更合理。(2)在得到特征矩阵H后,采用式(3)计算注意力系数,该过程不涉及可训练参数,可以有效降低计算复杂度。
在归一化前,图注意力权重见图4。随着图注意力卷积层数的加深,节点和节点对于、之间链接存在性的影响逐渐增大,而节点对于链接的存在性的影响降到最小。在此基础上,对应于图2 中排序池化层所展示的,可以更果断地将节点的特征向量去除。
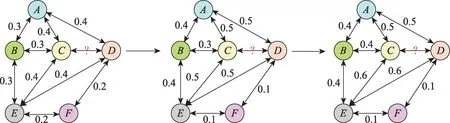
图4 softmax 前图注意力权重示意图Fig.4 Graph attention weights before softmax

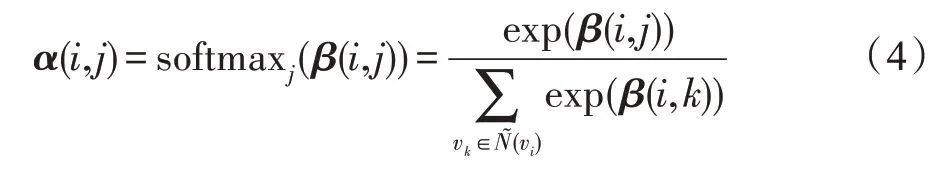
在得到归一化后的双向注意力权重后,第+1层的输出为:


1.2 全局特征提取模块
本模块利用struc2vec 节点嵌入算法提取结构特征。该算法利用图中每对节点不同邻域范围的结构距离构建多层图,并利用迭代公式将多层图转化为聚合图,然后利用随机游走和SkipGram 生成节点序列和节点嵌入向量。具体过程见图5,可分为四步。
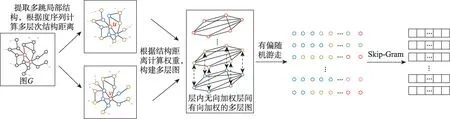
图5 全局特征提取模块Fig.5 Global feature extraction module
(1)度量结构相似性
度量结构相似性时不使用节点或边的属性信息,也不基于任何特定的相似性度量。此处的相似性仅仅依赖于节点的度,这种相似性是分层的,随着邻域范围不断增加,可以捕获更精确的结构特征相似性。对于两个节点,如果它们的度相同,它们是结构相似的,而若它们的邻居具有相同的度序列,则它们更加结构相似。
对于图=(,),=||表示图中的节点数。若有图中的节点,R()定义为的第跳点集。对于⊂,()表示中节点的有序度序列。令为图的直径,指图中任意两个节点间距离的最大值。对于图中任意两节点、的跳子图,=0,1,…,,考虑它们在层的结构距离定义为:
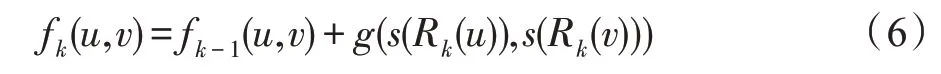
其中,=0,且|R()|,|R()|>0,度量了两个有序度序列的距离。注意只有当节点和均有跳邻居时,f(,)才有意义,当或不存在跳邻居时,与在多层图的第层无边相连,见式(9)。
采用动态时间归整(dynamic time warping,DTW)算法计算度序列的距离。对于两个有序度序列、,匹配它们中的每一个元素、,每一对元素的距离定义为:
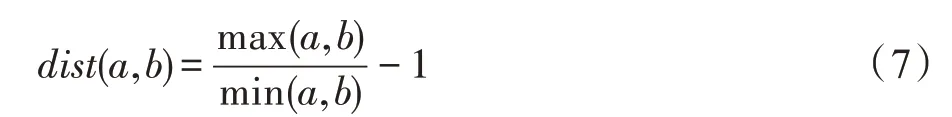
和的距离即为所有元素对距离之和。
另外,为了降低DTW 算法计算结构距离的时间复杂度,令′、′分别为度序列、的压缩形式,=(,),=(,)分别是′、′中的元组,元组中和表示度值,和对应和出现的次数。式(7)调整为:
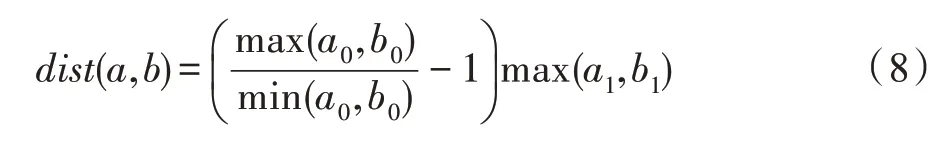
(2)构建多层图
利用结构距离构建多层图。由于多层图内存消耗较大,为了降低复杂度,在度量结构相似性时没有必要计算每个节点与其他-1 个节点的相似性,即多层图的每一层并非完全图。将原始图中的节点度按序排列,对每个节点,在度序列前后各选取lb个节点与其连接。另外当多层图的层数接近时,跳邻居数较少,度序列的长度相对较短,f(,)与f(,)差别不大。故对于层数,选取一个固定值′<,能有效降低构建多层图的计算和内存需求。
此时构建的多层图是层内无向加权层间有向加权的。式(9)表示层内权重,在第层,两个点、的结构距离越远,权重越小。只有当f(,)有意义时,、在层才有边相连。
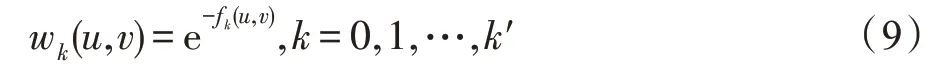

(3)生成节点序列
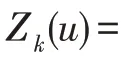
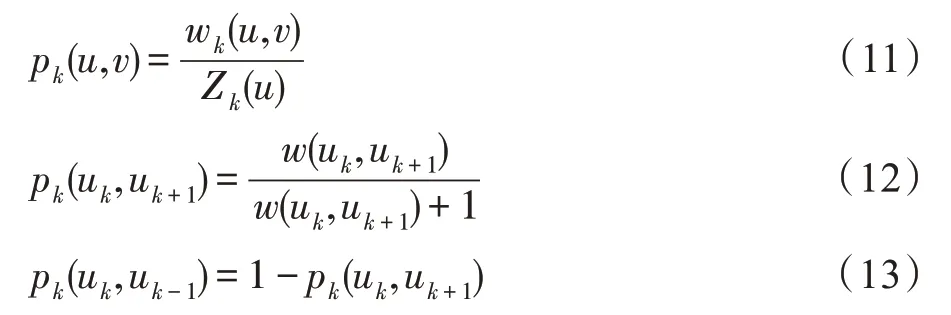
进一步地,为了降低I/O 时间、内存消耗以及磁盘消耗,利用式(12)的层间权重将多层图中的信息汇聚到同一层,生成聚合图。为此要求每一层节点间的连接情况完全相同。
在多层图中,每个节点与2×lb个节点相连,但是根据式(6)和式(9)可知,每一层的连接情况可能不同,因为当或在跳无邻居时,f(,)无意义,此时,在层无边相连。为了使每一层的连接情况完全相同,对于在第0 层有边相连的节点对,,若它们在>0 层无边相连,则令w(,)=0。
在保证每层节点间连接情况相同后,提出迭代公式(14),利用多层图中的信息生成聚合图。
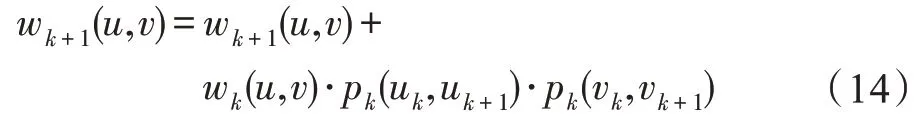
根据式(6)、式(9)和式(11)可知,在低层结构特征不相似的节点对在高层一定不相似;两个节点结构特征越相似,节点间边的权值越大,转移概率越大。因此,如图6 所示,对于节点(,)在信息聚合过程中有三种情形:
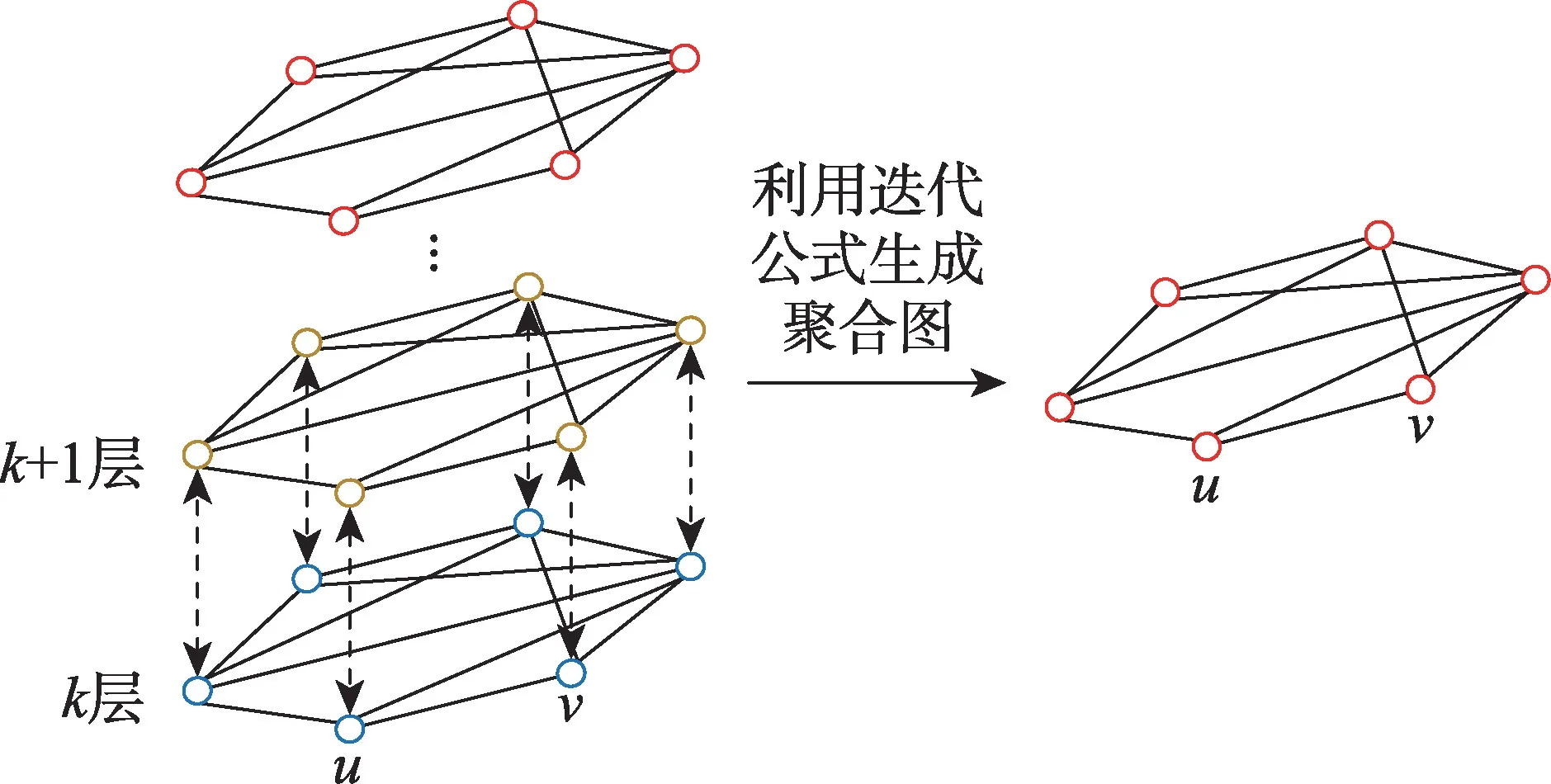
图6 聚合图Fig.6 Agglomerative graph
若节点对(,)在层结构特征不相似,则在+1 层一定不相似,由多次小权值累积,可以得到更加精细的权重。
若节点对(,)在层结构特征相似,在+1 层也相似,低层的权重汇聚到高层降低了其影响力,倾向于依赖高层权重进行随机游走。
若节点对(,)在层结构特征相似,在+1 层不相似,通过迭代公式减小从层获得的权值,倾向于利用+1 层的权重与情形2 区分。
综上,利用式(14)生成的聚合图具有三个显而易见的特性:低层的权重汇聚到高层降低了其影响力;结构特征越相似的节点对之间的权重越大;聚合图上的有偏随机游走不存在层的切换,相较于多层图,聚合图的内存和磁盘占用更少。
(4)生成节点嵌入向量
在聚合图上通过有偏随机游走得到节点序列后,利用自然语言处理模型SkipGram 生成嵌入向量。给定一个节点,SkipGram 的目标是最大化其上下文出现在序列中的概率,其中节点的上下文由以其为中心的大小为的窗口得到。
对于这一任务,采用分层softmax 优化策略,通过霍夫曼二叉树计算条件概率。对于窗口内的节点∈,在霍夫曼二叉树中有一条由树节点构成的路径,,…,b,其中为根节点,b即为节点,有:

其中,是二元分类器逻辑回归。
2 实验
本章在第1章的基础上,将衍生出的模型ASEAL(learning from subgraphs,embeddings and attributes for link prediction with attention mechanism)、DNSL(learning from double-radius node labeling,node2vec and struc2vec for link prediction)以及最终模型ADNSL与启发式方法、节点嵌入算法还有神经网络模型在八个数据集上进行了全面的对比。本章接下来主要介绍数据集、评价指标、负注入、模型结构及超参数设置,并进行实验对比分析。
2.1 数据集
实验包括八个真实数据集:USAir(美国航空线路网络)、NS(网络科学研究人员协作网络)、PB(美国政治博客网络)、Yeast(蛋白质交互网络)、C.ele(秀丽隐杆线虫的神经网络)、Power(美国西部电网)、Router(路由器级因特网)和E.coli(大肠杆菌代谢产物成对反应网络)。八个数据集涉及的领域有交通网络、社交网络、生物网络等。它们的具体信息见表1,其中||为网络中节点数量,||为网络中边的数量。
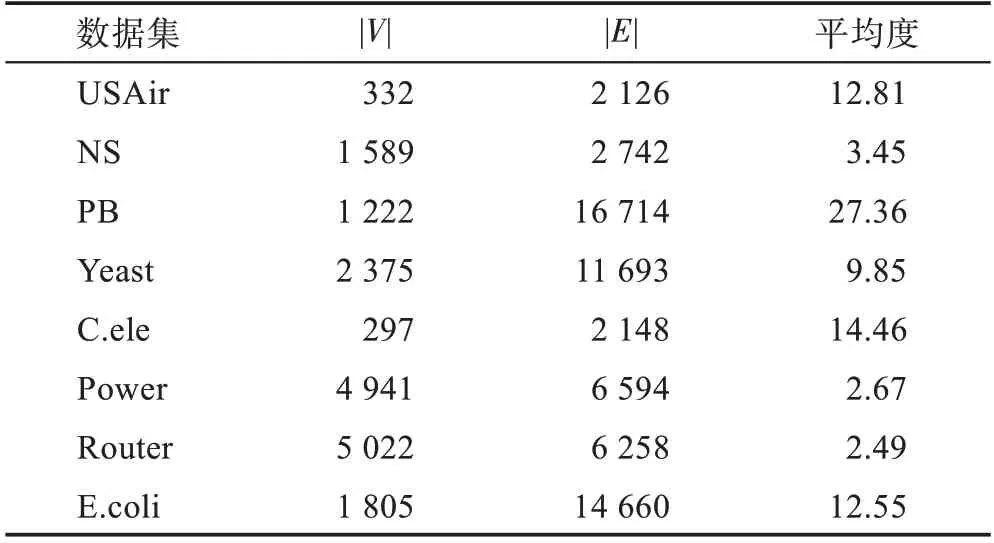
表1 实验数据集Table 1 Experiment datasets
2.2 评价指标
本文的实验结果主要使用ACC(准确率)和AUC(ROC 曲线下面积)评估二分类的优劣。每个实验进行30 次,取平均值作为实验结果。
对于每个数据集,将网络中存在的链接随机分为训练正例和测试正例,并选取等量的不存在链接的节点对作为训练负例和测试负例。在实验中,考虑了50%和90%的链接作为训练正例两种情况。另外,在生成节点嵌入特征之前,需将测试正例从网络中移除以防止测试集泄露。
2.3 负注入
假设给定网络=(,),有训练集正例⊂,以及训练集负例⋂=∅。在网络上利用节点嵌入算法得到的嵌入向量作为节点特征。若该过程记录了网络中某些边的存在信息,即,则在神经网络训练过程中,仅仅对这部分信息进行拟合就能得到很好的训练效果,但是这会导致模型的泛化性能很差。因此,对于存在这一问题的节点嵌入算法,通过负注入将训练集负例加入网络中,即在′=(,⋃E)上学习节点嵌入向量,可以有效地提高泛化性能。
在局部特征提取中,特征矩阵包含节点标记矩阵和节点嵌入矩阵两部分。如果直接在上利用node2vec 提取节点嵌入向量,由于随机游走过程依赖于网络中存在的边,该过程会记录边的存在信息,图神经网络只需要对这部分信息进行拟合即能得到很好的训练效果,但是在测试时模型的泛化性能很差。因此node2vec 需要在负注入后的′=(,⋃E)上学习节点嵌入向量。
与node2vec 不同,在利用struc2vec 提取全局结构特征时,使用负注入是不合理的。struc2vec 在生成向量表示过程中,仅仅利用了节点度信息,且随机游走是在重构的聚合图上进行的,未涉及原图中任何边信息。若struc2vec 在负注入的图上生成节点嵌入向量,反而会对节点度和节点结构特征产生较大影响,严重影响性能。经过实验发现,不使用负注入的struc2vec 可以保留更有效的结构特征相似性,对链接预测的效果有显著提高。
2.4 模型结构及超参数设置
局部特征生成模块的输入为目标链接一跳或两跳子图,∈{1,2}。对于SEAL 和DNSL,为了适应内存,数据集PB 和E.coli 选择=1,其余数据集=2。对 于ASEAL 和ADNSL,数 据 集NS 和Power 选 择=2,由于加入了双向注意力机制,为了适应内存,其余数据集=1。另外,对于E.coli,限制子图中最大节点数为150。特征矩阵中node2vec生成的节点嵌入向量为128 维,node2vec 有偏随机游走参数=1,=1,游走路径数为10,路径长度为80,SkipGram 中窗口大小为10。
局部特征生成模块采用四个图卷积层,通道数分别为32、32、32、1。为了方便起见,仅使用最后一层通道排序,排序后,截取行,其中值使得60%的子图的节点数大于。接下来是两个一维卷积层,输出通道数分别为16 和32。第一个卷积层的输入维度为97×1,卷积核大小为97×1,卷积核个数为16,步长为97,输出维度为×16,之后的最大池化层的卷积核大小为2,步长为2。第二个卷积层的卷积核大小为5×16,卷积核个数为32,步长为1。图卷积层使用tanh 作为非线性函数,在其他层中使用ReLU 作为激活函数。
全局特征提取模块中,struc2vec 将′=6 的多层图的信息汇聚到单层图,生成32 维的节点嵌入向量,并将64 维的目标链接节点向量表示输入到全连接层。与node2vec 相同,对于聚合图上的随机游走,每个节点的游走路径数为10,路径长度为80,SkipGram中窗口大小为10。
局部特征生成和全局特征提取模块的输出维度均固定为64 维。全连接层的隐藏单元数为128,dropout比率为0.5。
2.5 实验结果及分析
表2 和表3 分别是50%和90%的链接作为训练正例的情况下,模型性能的对比,其中带下划线的AUC为次优的,加粗的AUC 为最优的。
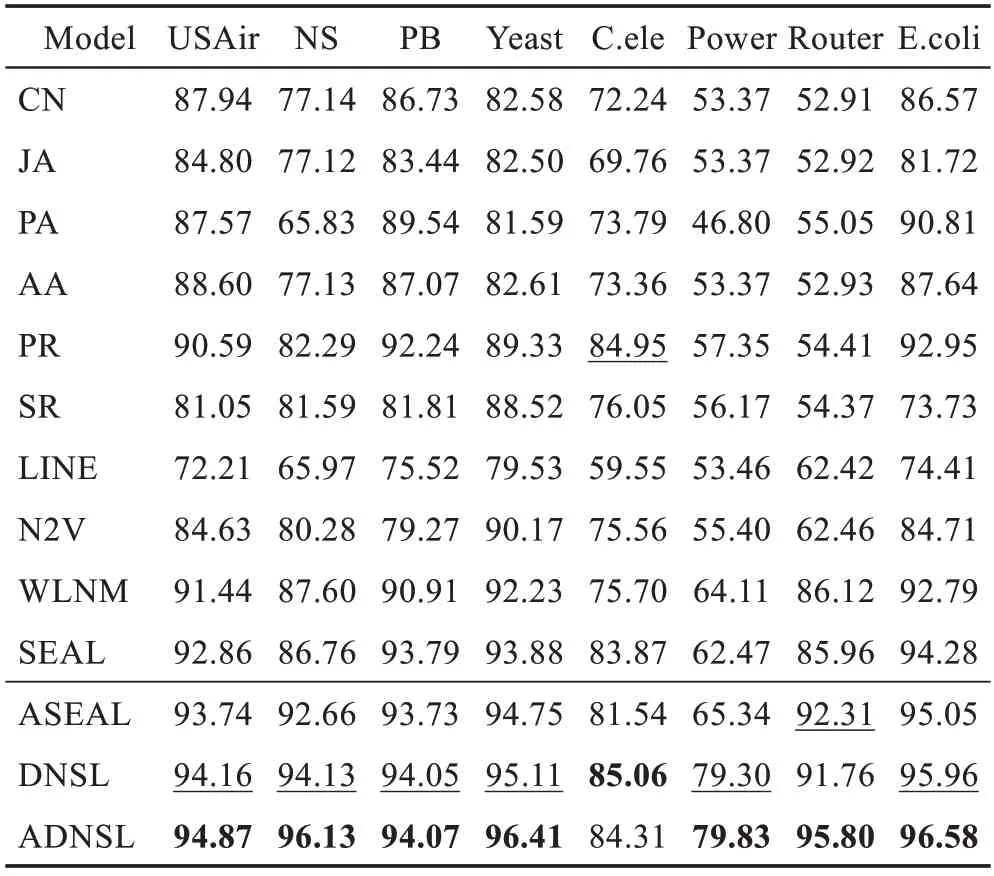
表2 模型AUC 对比(50%训练链接)Table 2 AUC comparison of different approaches(50%training links) %
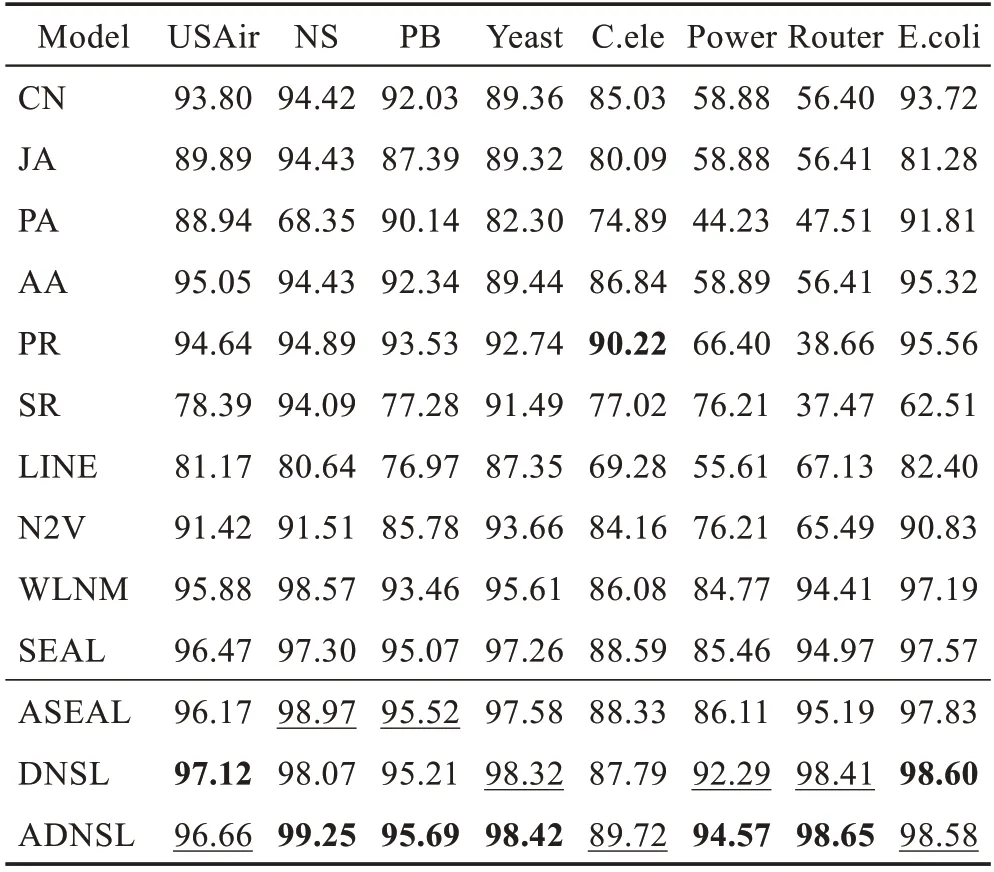
表3 模型AUC 对比(90%训练链接)Table 3 AUC comparison of different approaches(90%training links) %
表中前六个方法为引言中提到的链接预测启发式方法。
LINE 和N2V 为经典的节点嵌入算法,它们利用源节点周围的节点信息生成向量表示,进而用于链接预测。
WLNM 算法利用目标链接局部子图的节点标记重构邻接矩阵,输入全连接神经网络链接预测。
SEAL 算法是表现十分优异的链接预测算法,利用图神经网络学习局部启发式信息,进行端到端的链接预测。
ASEAL 是本文提出的结合双向无参注意力机制的SEAL 算法链接预测模型。
DNSL 是本文提出的链接预测模型,其中图卷积用于局部特征生成,struc2vec用于全局特征提取。
ADNSL 是本文提出的链接预测模型最终版本,结合多特征和图注意力卷积,可以显著提升链接预测的性能。
在八个数据集两种情况下,结合表2 和表3,可以看出:
(1)ASEAL 相较于SEAL 有一定程度的性能提升,说明融合双向无参注意力机制的图卷积模型,可以在一定程度上弥补特征无效性和节点无偏性。
(2)DNSL 模型利用图卷积作为局部特征生成模块,struc2vec 作为全局特征提取模块,可以有效结合局部和全局特征,很好地针对SEAL 的局部性获得图卷积部分无法学到的特征信息。
(3)ADNSL 模型相较于其他所有模型,均有非常显著的性能提升。相较于SEAL,尤其对于NS、Power和Router这三个数据集,ADNSL 的提升尤为明显,在表2 中AUC 值提升分别有10 个百分点、17 个百分点和10 个百分点左右。即使在表3 中,数据集中90%的边作为训练正例时,其他方法的AUC 表现良好,ADNSL 仍能有进一步提升。
对于NS、Power 和Router 提升十分明显的原因,分析认为:ADNSL 等模型对于平均度较小的数据集,可以更好地捕捉式(7)所示节点度序列的差异,进而区分节点结构特征。例如,度为1 和2 的节点之间的距离为1,要远远大于度为101 和102 的节点之间的距离1/101。
图7 为SEAL、ASEAL、DNSL 和ADNSL 四个模型在NS、Power 和Router 三个数据集,50%训练链接情况下,训练过程中LOSS 和ACC 值变化对比。
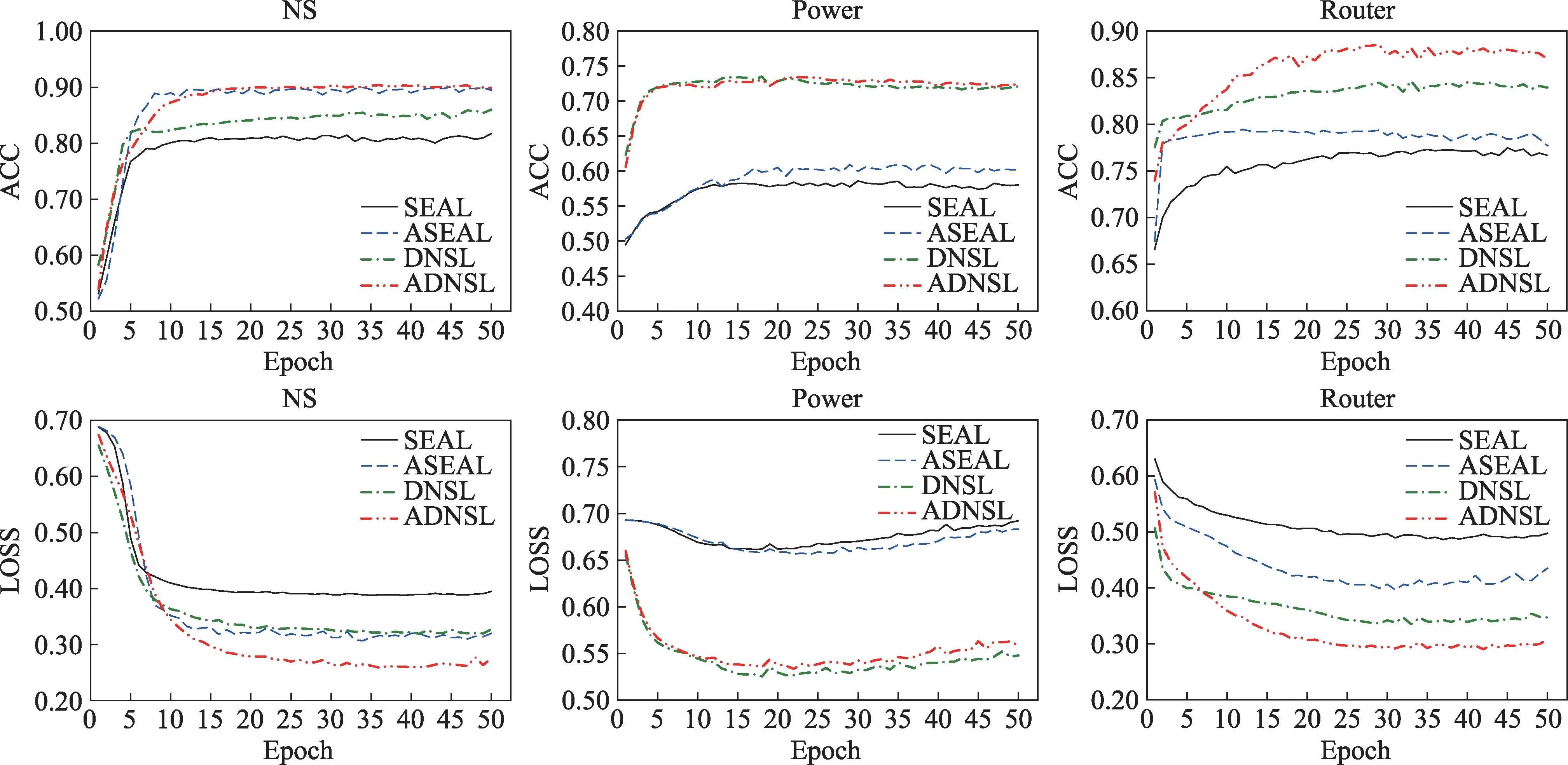
图7 收敛性分析(50%训练链接)Fig.7 Convergence analysis(50%training links)
可以很明显地看出,相较于SEAL,本文提出的模型训练起始值优于SEAL,且可以达到更优状态。对于Power 数据集,次优模型SEAL 在训练过程中的损失略有下降后,很快开始上升,而本文的模型可以较好地学习并达到稳定状态。另外目前基于图神经网络的链接预测算法一般可以在50 轮以内达到最优值,而WLNM 等基于全连接神经网络的算法往往需要100~150 轮才能得到稳定的结果。
3 结束语
在启发式方法和节点嵌入算法研究的基础上,利用神经网络自动学习启发式特征进行链接预测表现出优越的性能。本文在表现优异的算法SEAL 的基础上,提出了融合图注意力的多特征链接预测算法ADNSL。ADNSL 分为局部特征生成和全局特征提取两个模块,第一个模块利用双向无参注意力图卷积学习启发式特征,第二个模块利用聚合图提取目标节点的结构特征,然后将两个模块输出的特征向量利用全连接层融合。
两个模块的特征融合可以有效解决基准算法SEAL 的局部性。图注意力卷积中的双向无参注意力可以在一定程度上弥补特征无效性和节点无偏性。利用迭代公式生成的聚合图可以有效减少有偏随机游走的时间,降低内存消耗和磁盘消耗。
实验表明,本文提出的ADNSL 模型性能远超传统的启发式算法,优于SEAL、WLNM 等表现优异的神经网络算法。对于之前的工作中表现不理想的数据集,ADNSL 的表现有了巨大的提升。在未来的工作中,可以考虑更多更丰富的全局信息,例如社区信息(M-NMF、NECS 等)作为全局特征,进一步提高链接预测的性能。

