基于机器学习的跨海管道泄漏位置预测模型

卓美燕，林文介

(1.福建水利电力职业技术学院，福建 永安 366000； 2.福建省莆田水利水电勘测设计院有限公司，福建 莆田 351100)

输送石油、天然气、水等的管道系统会因为管道材料选择不当、接头薄弱、土方运动、泥沙等问题[1-3]造成管道泄漏。跨海引水工程，如国内的汕头市南澳岛供水工程[4]、獐岛农村引水跨海供水工程[5]等泄漏位置多处于海底，位置难以检测。

尽管泄漏检测和定位很重要，但目前对于管道的泄漏影响因素还没有很完善的研究。Ali等[6]将现有的检漏方法进行了分类：第一类方法依赖于从声学仪器、照相机、探地雷达(GPR)、光纤等收集数据[7-8]。这些方法的主要问题是可扩展性差、安装和维护成本高、功耗高。第二类方法是使用水力学稳态方程计算得出泄漏位置，瞬态流在网络发生泄漏时可以带来更多的信息。该方法将传感器收集到的瞬态水利参数与稳态方程的计算参数进行比较[9]，通过参数的差异识别异常情况。但研究表明，该方法在泄漏量比较轻微或者背景噪声较大时精度较低[10]。第三类方法是依靠传感器的实时数据结合机器学习进行预测，Soldevila等[11]提出了一种基于分类器(K- Nearest Neighbor和Bayes)和压力模型的配水网络(water distribution networks,WDNs)泄漏检测方法，通过收集压力数据，然后应用K-Nearest Neighbor和Bayes分类器获取残差，以确定泄漏位置。该方法的优点是采集和传输数据的时间间隔较短，成本较低，可考虑因素较多。

本文以莆田平海湾跨海供水应急工程为例，使用EPANET软件建模，分析使用水力学方程计算和使用多种神经网络进行预测泄漏位置的可行性，并与实际工程结果进行比较，以期能为跨海输水管道泄漏问题提供参考。

1 研究方法

1.1 EPANET软件

EPANET软件是由美国国家环境保护局开发的管网模拟软件，可用于模拟世界各地的水分配系统，也常用来模拟水分配系统中的泄漏情况[12-13]。建立好管网模型后，EPANET可以对管网的水利、水质等各种特征进行模拟，来跟踪管道流量、节点压力、水龄以及模拟期间整个网络的水源等。

1.2 泄漏预测方法

1.2.1水力学稳态方程

跨海管道中，依据重力场中不可压缩流体恒定流的Bernoulli’s方程，对于管道中任意两节点有如下方程：

(1)

式中：z1、z2分别为输水管道1、2节点的当地高程；p1、p2分别为输水管道1、2节点的内水压力；v1、v2分别为输水管道1、2节点平均流速，沿程不变；h2为输水管道2节点总水头损失，包含沿程水头损失hf和局部水头损失hj；ρ为水的密度；g为重力加速度。

实际工程中，管道泄漏处的总水头难以测得，因此该计算方法只适用于完全泄漏时，即泄漏处流量等于总流量且泄漏处管道流速与海面近似(v2=0)，因此令

(2)

式中：h1为陆地上测压管所测水头；h3为潮平面水头。

输水管道和配水管道的hj可按hf的10%计算，将式(2)代入式(1)可得：

h2=h1-h3=1.1hf

(3)

根据Hazen-Williams方程，泄漏处距陆地测压管距离为

(4)

式中：Lleak为计算管段的长度；h2为单位管长水头损失；C为Hazen-Williams系数，本文管道为钢丝网骨架聚乙烯复合管材质，根据SL 310—2004《村镇供水工程技术规范》取为130；Q为管段流量；d为管道直径。

1.2.2支持向量机模型

支持向量机(support vector machine，SVM)是将输入向量非线性映射到一个高维特征空间的机器学习模型[14]，在这个特征空间中根据选定的核函数构造了一个线性决策面，决策面的特殊性质保证了学习机具有较高的泛化能力。SVM用于回归问题时，对于特定的训练样本集D={(x11,x12,…,x1n,y1),(x21,x22,…,x2n,y2),…,(xn1,xn2,…,xnn,yn)}，希望能够得到一个f(x)使其与y尽可能接近。与SVM不同，支持向量回归(support vector regession,SVR)允许f(x)与y之间差值大于误差ε时才计算损失。当训练样本落入宽度为2ε的样本带时，预测被判断为正确。

1.2.3BP神经网络模型

反向传播神经网络(back propagation neural network，BPNN)是一种最常用的前向神经网络[15]，又称误差反向传播网络，是一种多层映射网络，在信息向前传播的同时，最大限度地减少反向误差。单隐层BP神经网络可以近似任意精度的任何非线性函数[16]。BPNN使用梯度下降算法进行优化[17]：首先，对网络的连接权值和阈值进行随机初始化；然后，利用训练样本调整网络的连接权值和阈值，通过梯度下降使网络输出值和实际值的均方误差(MSE)最小。单个隐含层BPNN由输入层、隐含层和输出层组成。相邻层通过权值连接，权值总是分布在-1和1之间。

1.3 模型框架

本文采用相关系数和均方根误差对不同模型的预测结果进行评价。对于管道泄漏位置预测问题，对比了2种机器学习方法的预测精度，分别构建了K-CV-SVR模型和BP神经网络模型，图1为2种机器学习模型的流程，主要分为两部分：

图1 BP神经网络模型和K-CV-SVR模型流程

图2 EPANET构建的供水管道模型

a.首先使用SVM-SCALE程序对初始数据进行归一化，形成训练集和测试集。然后使用K-CV方法对SVR模型中参数c和g进行寻优，将获得的最优参数分别带入核函数。使用不同的迭代次数计算SVR模型的相关系数和均方根误差判别预测模型的好坏，最终将测试集带入SVR机器学习模型输出预测值。

b.将训练集的数据分别带入BP神经网络不同的激励函数中，由于输入输出层各有3种激励函数和5种学习算法，对各种函数和算法的组合进行遍历，选出满足误差条件的最优函数和算法组合，带入训练集构建预测模型。最后将测试集带入预测模型得到管道泄漏位置的预测值。

2 实例验证

2.1 EPANET模型构建

莆田平海湾跨海供水应急工程位于秀屿区东南部，主要解决南日岛和平海湾缺水问题，是一项民心工程。南日海岛岛内居住约5.6万人，地表水人均不足300 m3，属极度贫水区[18]。为解决岛上军民的用水问题，当地政府决定建设平海湾跨海供水工程。设计日供水规模6.5万 t，水源来自东圳水库，取水口驳接北岸供水工程笏石新厝店分叉口，建设东峤、南日水厂各一座，中途建加压泵站两座。供水主管道长44.06 km，其中海底管道长9.86 km。海底管道采用钢丝网骨架聚乙烯复合管，管径为500 mm，其余管段为直径500 ～800 mm的玻璃钢管。已知平海湾跨海供水管网的基本参数，如各管段材料、管长，各节点高程等，使用EPANET软件构建其基础模型，如图2所示。

2.2 训练集样本获取与处理

当管网存在泄漏时，前后管段的压力和流量会发生改变，并且和泄漏量有关。因此前后管段的流量读数和压力读数具有很强的特征性，考虑到实际测量数值的方便性，本文采用海底管道在陆地两侧的管段流量作为输入样本。

模拟漏失形式时，使用EPANET自带的射流点模型。射流点是EPANET模型的节点属性之一，通过射流点的流量与该节点压强的关系如下：

q=Clpγ

(5)

式中：q为节点的流量；p为压强；Cl为流量系数；γ为压强指数，对于喷嘴，γ=0.5。

射流点可以模拟与连接节点相连的管道渗漏，节点的渗漏情况与压强系数和流量系数均有关，EPANET只支持对流量系数的修改，所以本文调整不同的节点流量系数以模拟现实中可能发生的泄漏情况。节点流量系数调整的最大值为使后管流量为零的值，选择范围从0至最大值均匀四等分的4组节点流量系数作为试验参数。模拟泄漏点的间隔为200 m，因此对于总长约10 km的海底管道，得到200组流量作为输入样本，200个泄漏点位置作为输出样本，即输入样本共计200×2个数据。200个输出数据。在神经网络训练时随机选取60%的数据作为训练集数据，15%的数据作为验证集数据，25%的数据作为测试集数据。

2.3 BP神经网络模型优化

隐含层层数与节点个数会影响BP神经网络的阈值和权值大小，输入数据经过隐含层进行加权求和，随后将求和的值通过方程映射获得预测值和实际值的差会反向传播到学习算法中，学习算法进而对隐含层的阈值和权值进行调整。因此隐含层层数和学习算法的选取对于BP神经网络十分重要。

2.3.1隐含层层数寻优

由Kolmogorov定理可知

(6)

式中：n2为隐含层节点数；n1为输入层数目；o为输出层数目；a为隐含层调节常数，取值范围为1～10。因此该模型的隐含层数目范围为3～12。

2.3.2学习算法寻优

BP神经网络常用的学习算法有trainlm、trainbr、trainscg 3种，3种学习算法分别搭配3～12层隐含层，得到了30个BP神经网络模型，对这30个神经网络模型进行训练，迭代次数设置为1 000次，结果见表1。由表1可以发现使用trainbr学习算法，隐含层层数取11时得到的相关系数最大，均方根误差最小，因此本文选取隐含层层数为11的预测模型。

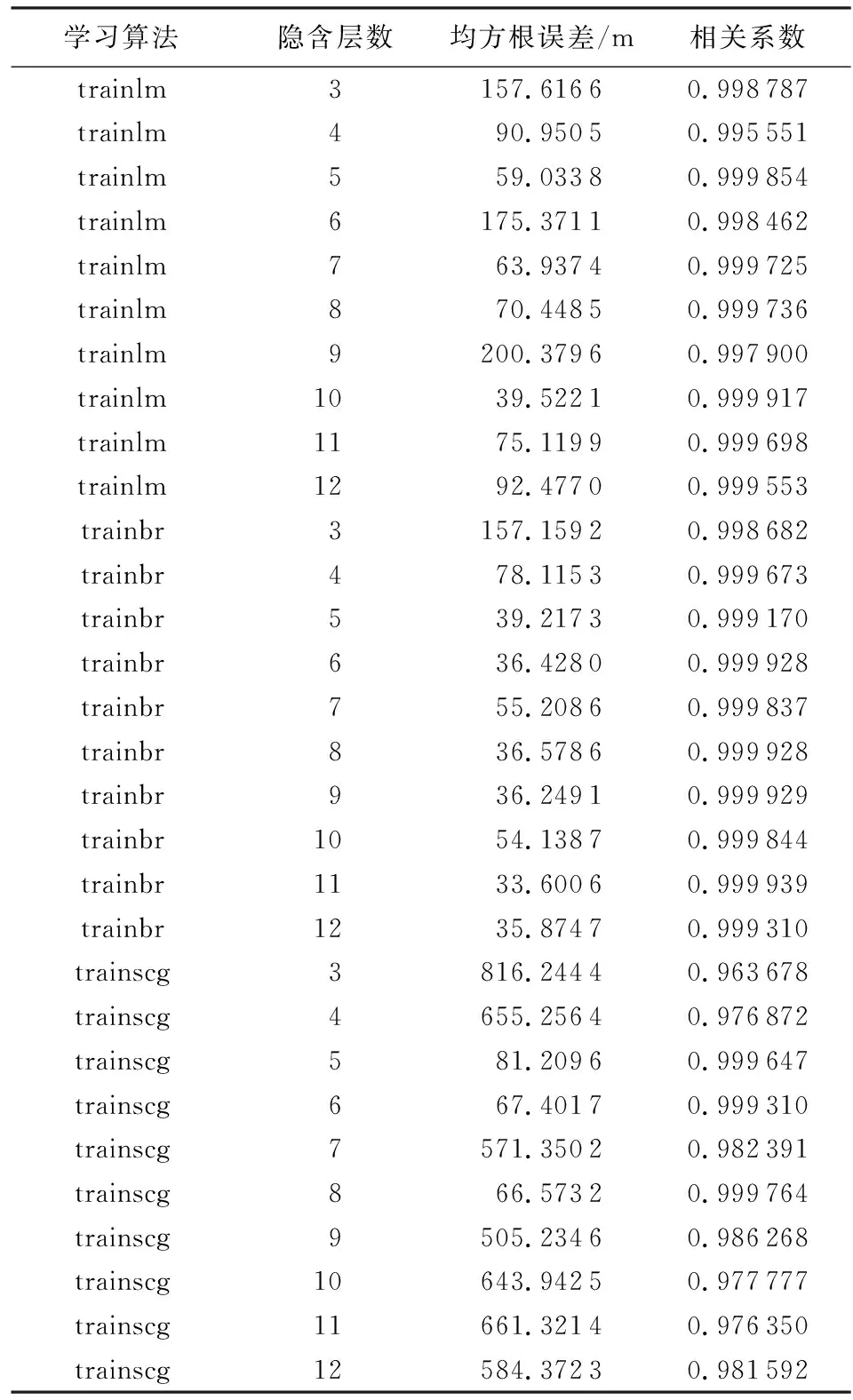
表1 BP神经网络模型不同学习算法和隐含层层数的均方根误差和相关系数

2.4 K-CV-SVR模型

a.数据归一化。由于输入的流量数值范围大，波动大，为了避免产生奇异数据，导致模型收敛速度慢，预测精度降低，使用数据归一化将输入的两组流量按照公式映射到[-1,1]区间内。

b.K-CV方法寻优惩罚系数c和核函数参数g。惩罚系数c和核函数参数g对SVR回归模型的回归效果十分重要，过高的c会导致回归模型过学习，降低预测精度，同时增加了学习时间，提升了收敛难度；过低的c会导致回归模型欠学习，无法满足要求。本文采用了K-CV(交叉验证)方法对c和g进行寻优。设置交叉验证的均方根误差小于105，多次试验确定log2c范围在[12，13]，log2g范围在[7，8]，采样步长为0.1，当均方根误差低于105时停止寻优，最终得知log2c取12.5，log2g取7.6时均方根误差最小。

c.核函数的选择。SVR模型常用的核函数类型包括线性核函数、多项式核函数、RBF核函数、Sigmoid核函数4类，设定SVM类型参数为3，损失函数值为0.1，nu值设置为0.5，分别用训练集训练4种核函数，获得模型后输入训练集进行预测，计算4种模型的均方根误差和相关系数，结果见表2。由表2可知，使用RBF核函数进行预测的均方根误差仅为114.36，相关系数为0.998 61，明显优于其他种核函数，相较于其他核函数能够更加准确的通过流量预测管道泄漏的位置。

表2 不同核函数的迭代次数、均方根误差和相关系数

2.5 EPANET模型预测效果分析与评价

将EPANET建模获得的数据进行归一化，并分别带入BP神经网络模型、K-CV-SVR模型以及未优化的SVR模型中进行训练和预测；同时使用EPANET软件建立9个在不同位置的完全泄漏(泄漏点流量等于总流量)的测试集带入2种机器学习模型中预测，并与传统水力学稳态方程进行比较。

2.5.1部分泄漏情况预测

归一化的EPANET数据随机选取60%和15%作为训练集和验证集，分别代入3种模型中进行训练。得到训练的模型后将剩余25%测试集数据代入模型进行预测，结果如图3所示。

由图3可知，对于提供的测试集，3种机器学习模型都能够较好地预测泄漏节点的所在位置，且BP神经网络模型在大部分测试点的预测精度均高于其他2种模型。进一步计算了3种模型的均方根误差和相关系数，结果见表3。由表3可见，经过K-CV参数优化的SVR模型精度有显著提高，但是预测精度还是低于BP神经网络模型，BP神经网络模型和K-CV-SVR模型的相关系数都高于0.995，证明运用这2种机器学习模型预测管段泄漏具有一定的可行性和可信度。

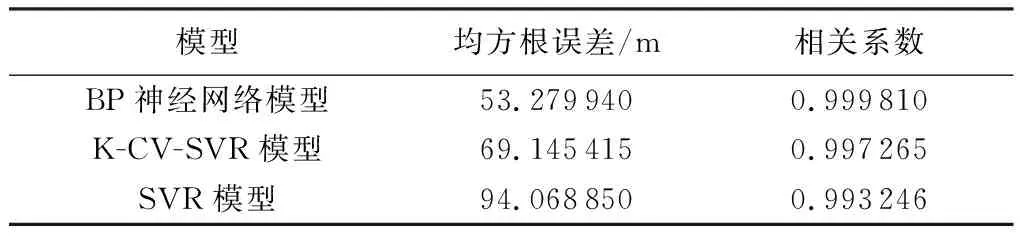
表3 3种模型预测结果均方根误差和相关系数

2.5.2完全泄漏情况预测

对于完全泄漏的情况，使用BP神经网络模型、K-CV-SVR模型和水力学稳态方程进行预测。由表4可知，对于前2个泄漏位置较靠近始端的测试点，3种模型的相对误差都较大，随着泄漏位置逐渐远离管道始端，2种机器学习模型的预测精度上升，水力学稳态方程预测精度降低，推测是由于方程设定的Hazen-Williams系数过小，由管道摩擦引起的水头损失偏小，致使预测精度随泄漏位置距始端长度增加而增加。但是由表4看来，3种预测模型的绝对误差都小于200 m，对于实际工程问题完全能够接受。

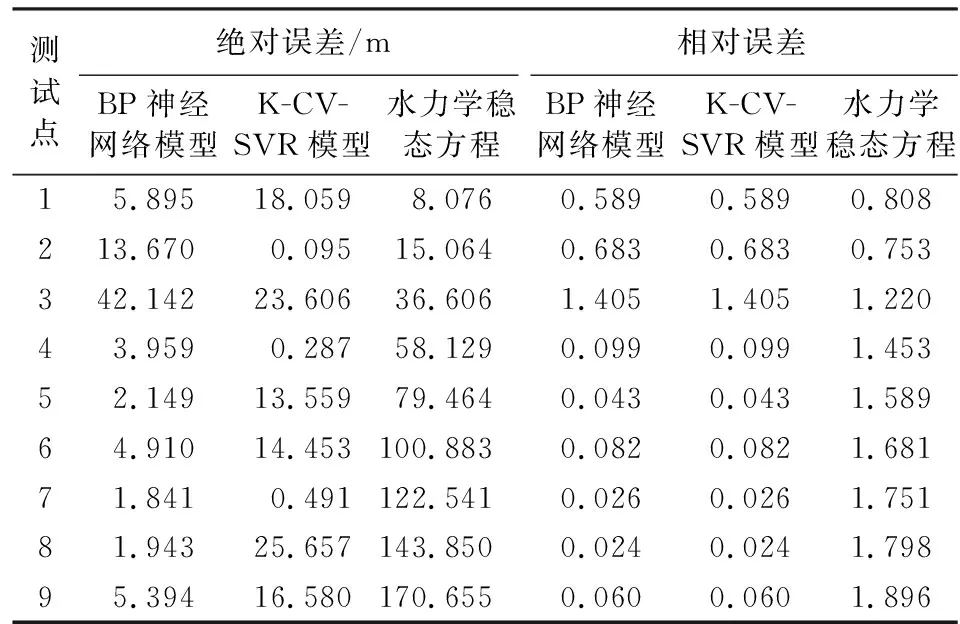
表4 BP神经网络、K-CV-SVR模型和水力学稳态方程预测结果的绝对误差和相对误差

2.5.3工程实例问题预测

在2016年左右，从笏石到南日岛段引水工程海底管道段突然出现一处泄漏，测得海底管道始端流量在0.135～0.137 m3/s之间，末端管道流量为零，使用测压管测得海底管道始端和潮平面水头差为9.2 m，将上述数据分别带入预测模型中对与泄漏位置进行预测，结果见表5。

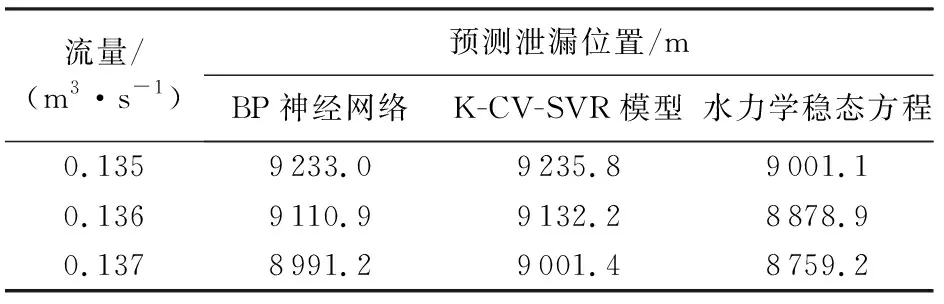
表5 BP神经网络、K-CV-SVR模型和水力学稳态方程预测结果

由表5可以发现3种模型预测泄漏位置都在9 km附近。事实上，利用物理介质油和乒乓球标识，并在海上大致范围搜寻并探测得知，海底管道确实是在距海底管道始端约9 km处发生了泄漏，进一步证实了使用机器学习预测的可行性和可靠性。

由上述实例可以发现，在海底管道泄漏位置预测中，机器学习模型和水力学稳态方程能够较好地通过海底管道始端和末端的流量大小海底管道泄漏位置。相较于水力学稳态方程预测，机器学习预测模型能够适用于更多泄漏场景，BP神经网络模型相较于其他预测模型拥有最好的预测精度，可为今后的海底管道泄漏位置预测提供参考。

3 结 语

本文通过EPANET软件建立了海底管道泄漏模型，克服了难以进行海底管道泄漏试验的问题，对于海底管道不同位置泄漏以及不同泄漏情况进行了模拟获得了充分的训练和测试数据。为提升机器学习模型的准确性和稳定性，对BP神经网络的隐含层数和学习算法进行寻优，最终确定隐含层数11和学习算法trainbr作为最终预测模型。使用K-CV方法对SVR算法进行参数优化，确定最优的log2g和log2c分别为7.6与12.5，确定RBF核函数为最佳核函数，避免了SVR常见的过学习情况。实例结果发现K-CV方法能够充分优化SVR模型，但预测精度弱于BP神经网络模型。

通过建模和工程实例验证表明，机器学习预测模型能够较好地通过管道流量变化预测海底管道泄漏位置。本文建立的海底泄漏模型仅考虑一处泄漏的情况，在实际工程问题中很可能出现多处泄漏的情况，因此管道流量和管道泄漏位置可能有更复杂的映射关系，而机器学习预测模型的准确性就存在未知，需要更深入的研究。未来应该加强对于机器学习参数优选的研究，多比较不同机器学习模型的优劣，使之更好地应用于海底管道泄漏的预测中。