基于高斯粒子滤波与消息传递的协同导航方法

陈明星，熊 智,2，王 融,2，刘建业,2，熊 骏，田世伟

(1.南京航空航天大学自动化学院导航研究中心，南京 211106；2.先进飞行器导航、控制与健康管理工业和信息化部重点实验室，南京 211106；3.南京邮电大学物联网学院，南京 210023；4.国防创新研究院，北京 100000)

近年来无人机集群由于其高效率、功能分布化等优势在军事和民用领域都取得了广泛的关注。导航信息是无人机可靠飞行的关键，尤其是在密集编队飞行环境下，无人机需要高精度的位置、速度信息来实现精确控制和防撞[1]。惯性/卫星组合导航系统是目前最广泛应用于无人机的导航手段，基于卫星导航的RTK技术可以为无人机提供厘米级的定位精度[2]。但为集群中所有无人机配备RTK 设备的成本较高，且在某些受限环境下如城市、森林等，GNSS 接收机可能因为无法搜索到足够的卫星而无法提供精确可靠的导航信息[3]。

为了充分利用集群的优势，国内外学者开始研究融合无人机机间量测信息的协同导航方法。文献[4][5]通过卡尔曼滤波实现本地量测与协同网络中相对量测信息的融合。以卡尔曼滤波为基础的分布式协同导航方法实现简单，但仅对相邻节点的协同信息进行了融合，没有充分利用网络中非相邻节点的约束关系。因子图为协同导航问题的处理提供了一个有效的框架，基于因子图框架的贝叶斯协同导航方法是目前协同导航领域研究的热点。文献[6]在GNSS 定位信息和无人机之间的距离信息基础上建立协同导航因子图，通过集群中少量配备RTK 设备的无人机辅助，提升了整个无人机群的定位精度。不过这种方法需要无人机群存在高精度定位节点，且每架无人机都能进行GNSS 定位。文献[7]提出了一种基于因子图和粒子化消息传递的混合和积算法（Hybrid Sum-product Algorithm for Wireless Network,H-SPAWN），能够将卫星伪距和用户间量测信息融合进行协同定位。该方法可以在卫星受限的情况下取得较好的定位性能，但该方法通过单一运动模型来描述载体的运动，不适用于复杂动态的无人机飞行场景，也无法提供连续可靠的导航信息。

本文提出了一种因子图框架下基于高斯粒子滤波和消息传递的协同导航方法，将INS 加入到因子图框架以描述无人机的动态过程，可以分布式地融合INS、气压计等本地传感器数据、卫星单差伪距以及机间测距信息，并通过无人机之间消息的迭代传递实现整个无人机群协同导航信息的有效融合，从而提升无人机群的整体导航性能。

1 协同导航因子图框架

考虑如图1所示无人机群工作场景，集群中所有无人机配备卫星接收机、IMU、气压高度计等导航设备，同时配备UWB 进行机间距离测量。在飞行过程中，无人机通过无线数据链与其他无人机交互导航信息，从而形成协同导航网络。

图1 无人机群协同工作场景Fig.1 Cooperative work scenario of UAV swarm

协同导航网络中导航状态的相互依存关系可以通过因子图来表示。以无人机的导航参数和IMU 的误差构成因子图的变量节点，无人机i在k时刻的变量集可定义为：

无人机在k时刻接收到的距离观测集和伪距观测集定义为：

其中：表示无人机i与j之间的UWB 距离观测，Ui为与无人机i存在距离观测的无人机集合，表示导航卫星sn（i）与无人机i之间的伪距观测，Si为无人机i搜索到的导航卫星集合。

由此可得无人机群导航状态的联合后验概率分布：

Zk表示k时刻无人机群接收到的所有观测信息：

根据无人机群的飞行特性和传感器特性，联合后验概率分布可被因式分解为如下形式：

其中，p（X0）表示导航状态的先验信息。结合式(5)和机载传感器类型，可定义四种因子：

• 惯性因子：

惯性因子连接无人机两个时刻的变量节点，表征导航状态的变化。

• 测距因子：

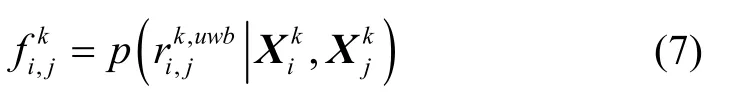
测距因子表征无人机i与j之间的距离关系。

• 高度因子：

高度因子表征无人机所在海拔高度与测得气压高度的关系，假设无人机飞行环境气压分布标准，则气压高度计得到的气压高度经过处理可视为海拔高度[8]。

• 单差伪距因子：

考虑到在城市等环境中无人机不一定能观测到足够的卫星实现定位，因此利用伪距作为观测信息。对于机载卫星接收机收到的伪距信息，其误差项中包含电离层误差和对流层误差在内的信号传播误差和卫星钟差通常可采用相应修正模型或星基增强系统播发的消息来消除，多径或非视距误差可通过故障识别的方式进行剔除，处理后的卫星伪距可建模为：

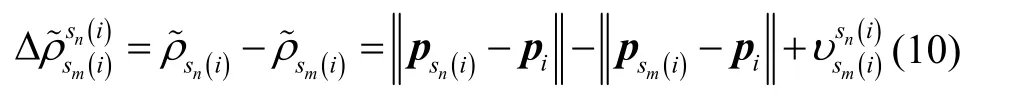
结合所定义的变量节点和因子节点，可将式(5)无人机群导航状态的联合后验概率分布分解和描述为图2所示因子图。在建立起协同导航的因子图框架，并完成变量节点和因子节点的建模后，本文结合高斯粒子滤波和消息传递算法设计协同导航方法，从而获得因子图中变量的最大后验概率估计。

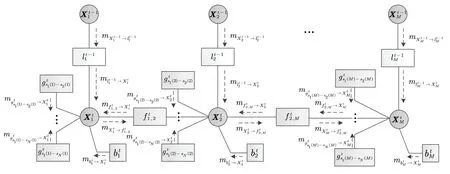
图2 无人机群协同导航因子图Fig.2 Cooperative navigation factor graph of UAV swarm

2 协同导航方法设计

协同导航因子图通过相邻节点之间的消息传递来实现概率分布的更新。本文利用一系列高斯粒子及其权重来对消息进行描述。因此，变量节点的概率分布估计问题转变为粒子值和权重的更新问题。

2.1 高斯粒子滤波

高斯粒子滤波的基本思想是将非线性系统中被估计状态的后验概率密度函数近似为多维高斯分布，利用粒子滤波技术求取高斯分布的相关参数并得到滤波结果[9]。对于一个随机系统，它的状态方程和量测方程的离散形式可以分别描述为：

其中f（·）和h（·）为已知函数；uk，υk分别为服从一定分布的系统噪声和量测噪声。高斯粒子滤波的目的是用一组粒子和权值来求取系统状态的边缘后验假设可由高斯分布近似逼近，高斯粒子滤波可以表述为：

其中Ck为归一化因子。

对于协同导航因子图来说，节点之间传递的消息包含了量测信息和变量的状态信息，消息的迭代传递过程即粒子的时间更新和量测更新过程。

2.2 消息形式

结合定义的因子类型，在协同导航因子图中需要考虑的消息主要有以下形式：

时进消息是由惯性因子传递给变量节点的消息，表示为：

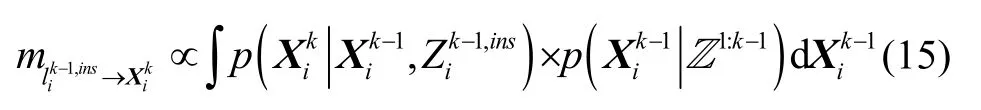
气压高度观测仅与当前时刻当前位置相关，因此气压高度因子与变量节点单连接，气压高度消息完全来自因子高度消息可表示为：

其中为无人机i在k时刻对应的海拔高度，为气压高度噪声方差。

与高度因子类似，由于卫星位置已知，单差伪距因子仅与变量节点之间单连接，因此，单差伪距消息完全继承自因子可表示为：

对于UWB 测距来说，在视距内的量测可建模为：

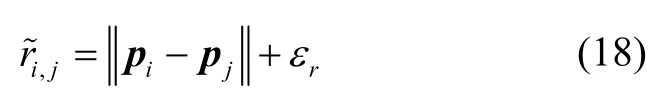
其中εr是方差为的测距噪声。由机间测距因子传递给变量节点的消息为：

式中为测距噪声和无人机j的位置协方差的叠加：

其中Hj→i为方向余弦：

变量节点传递给惯性因子的状态消息实质上就是变量节点自身状态的后验概率分布，其形式如下：

2.3 基于高斯粒子滤波和消息传递的协同导航方法实现过程

基于消息形式和高斯粒子滤波的相关定义，协同导航方法的实现过程如下：

①初始化各无人机的惯导系统和高斯粒子滤波器，给出导航状态的先验概率分布

③进行时进消息的传递，对所有粒子进行惯导递推，更新粒子的值，得到

④计算单差伪距消息和高度消息，更新此时的状态消息：

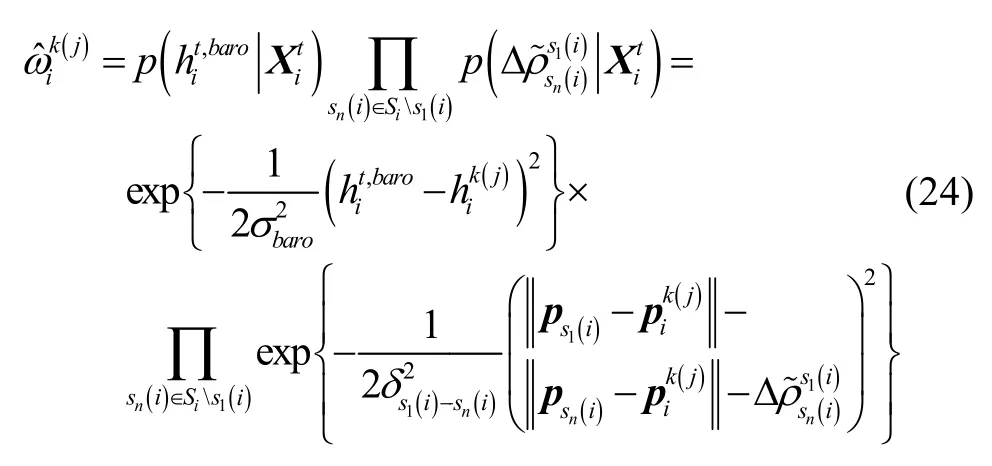
权重更新后对其归一化；

⑤测距消息的迭代传递，主要分为两步：

3 仿真验证与分析

3.1 仿真条件设置

根据第二节给出的协同导航因子图框架，对基于高斯粒子滤波和消息传递的协同导航方法进行MATLAB仿真验证。仿真条件如下：仿真10架无人机组成的无人机群，仿真时间3600s，无人机集群的初始位置和其中一架无人机的运动轨迹如图3-4所示，每架无人机粒子数目选定为2000，阈值α设定为0.01。每架无人机均配备IMU、气压计、卫星接收机和UWB，所有无人机均可与自身60m 范围内的相邻无人机测距和通信，每架无人机搜索到的卫星数为3颗，表1列出了无人机所搭载设备的仿真参数[10]。

表1 传感器配置与仿真参数Tab.1 Sensor configuration and simulationparameters

图3 无人机群初始位置Fig.3 Initial position of UAV swar m

图4 无人机运动轨迹Fig.4 Trajectory of UAV

3.2 仿真结果与分析

基于上述仿真条件，对无人机群的定位精度进行仿真分析。为了使验证具有代表性，将本文算法与无协同情况下基于卡尔曼滤波的INS/卫星伪距/气压高度组合、基于EKF的分布式协同算法以及基于H-SPAWN算法[7]的协同导航方法进行对比。以其中一架无人机的定位结果为例，仿真结果如图5所示。

由图5可以看出，本文所提出的协同导航方法相比无协同、基于EKF的协同方法以及基于H-SPAWN的协同方法定位精度得到明显的提升，为了定量地分析四种不同方法下的定位误差，对无人机群定位均方根误差(RMSE)进行了统计，统计结果如表2所示。表2中的位置估计误差的计算公式为：

图5 定位误差对比曲线Fig.5 Comparisonon position error

从表2可以看出，通过融合无人机之间的相对导航信息，基于EKF的协同导航方法提升了无人机群的定位精度，而通过对自身量测以及无人机群约束关系的充分利用，本文方法相对于基于EKF的协同导航方法定位精度提升89%，由于融合了INS信息，本文方法的定位精度同样优于基于H-SPAWN的协同方法，定位精度提升54%。

表2 定位误差统计结果Tab.2 Statisticsof position error

为考察本文所提出方法在可见卫星较少情况下的协同导航性能，在航迹、传感器配置等条件不变的情况下，设定无人机群中7架无人机可搜索到2颗卫星，初始高度最低的3架无人机无法搜索到卫星。图6给出了其中一架无法搜索到卫星的无人机的协同导航位置误差对比曲线，表3对比了该条件下的无人机群协同导航位置误差统计结果。

图6 定位误差对比曲线(可见星较少情况)Fig.6 Comparison on position error (Fewer visible satellites)

由图6和表3可以看出，在可见星较少的仿真条件下，无协同和基于EKF的协同方法定位结果已经发散，而基于H-SPAWN 的协同方法和本文方法由于充分利用了集群协同信息仍能实现定位。对比表2和表3可以看出，对于通过单一运动模型来描述载体的运动的H-SPAWN，在卫星导航信息减少的情况下其定位性能恶化程度要高于融合了INS信息的本文方法。本文方法相对于H-SPAWN方法定位精度提升了60%。

表3 定位误差统计结果(可见星较少情况)Tab.3 Statisticsof positionerror (Fewer visible satellites)

4 结论

本文以卫星受限环境下无人机群协同导航为背景，研究因子图框架下基于高斯粒子滤波和消息传递的协同导航方法，该方法利用因子图来描述无人机群导航状态与不同类型量测之间的关系，并通过高斯粒子滤波来完成因子图中节点间的消息传递，有效融合INS、气压高度、卫星单差伪距与无人机群相对量测信息，从而实现导航状态的后验概率估计。仿真结果表明，本文所提出的方法能够实现无人机群量测信息的精确融合，提升整个无人机群的定位精度，适用于卫星受限环境下无人机协同编队场景。