网格紧致化存储系统的分区设计和ABC分类分析
马云峰, 吴北平, 金钰清
(1.武汉科技大学 恒大管理学院,湖北 武汉 430065; 2.武汉科技大学 服务科学与工程研究中心,湖北 武汉 430065; 3.通城县第一中学,湖北 咸宁 437400)
0 引言
在自动化仓库存储系统中,控制成本是一个重要的管理问题,而仓库的大小与成本往往是正相关的,因此减少专用于存储的空间可以帮助控制仓储成本。在基于过道的存储系统中,通道占据了原本可以用来存放物品的空间,减少用于运输货物的通道大小和数量可以提高空间利用率。
基于网格的存储系统是受到儿童拼图游戏的启发(见图1),最早由Gue和Kim提出,称之为PBS(Puzzle-Based-Storage)系统,该系统使用单个或多个空位(escort)检索单位货物[1]。PBS的优点是提供更有效的空间利用、货物存储密度高、可以自动化完成并且能够利用近年兴起的智能控制和智能决策技术。

图1 一个15拼图
在实践和文献中,基于拼图系统的概念产生了几种紧致化存储系统变体。Furmans等[2]研究了网格流系统的设计,发现将I/O点放在一车一空位网格区域较长一边的中间是最优的。Alfieri等[3]在Furmans等[2]基础上探讨了车辆工具有限情况下的网格流系统。Gue等[4]基于相同数量的存储货物,研究网格存储系统的最优形态,针对网格存储系统提出分散评估协商的传输控制方案。Uludag等[5]研究了分散控制下的网格取货系统,该系统没有任何固定的通道和传送带,货物不会离开网格。Kota等[6]提出一个解决PBS系统中两个以上空位的启发式方案。Zaerpour等[7~9]提出了一个混合整数非线性模型,分析了具有两类存储的活立方体紧凑存储系统的响应时间,并通过最小化响应时间优化系统的尺寸大小和边界;然后进一步研究了基于多层的活立方体拼图存储系统,他们通过创建虚拟通道减少取货时间。
Yu等[10]假设多个货物和空位可以同时移动,即“块移动”(Block Move),设计了取货时间最短的精确算法。Mirzaei等[11]研究了一种PBS系统中同时取多个货物的启发式算法。Azadeh等[12]概述了自动化仓储的最新发展趋势,并对基于网格存储系统的性能提出了建模技术以及相应的解决方案。Yalcin等[13]分析了在网格存储系统中多智能体路径规划方法,一年以后Yalcin等[14]对网格中随机存在多个空位、最小化移动能耗为目标的问题进行了研究,不允许“块移动”,因此,在这个前提下能耗最小和时间最短是等价的。他们巧妙地设计了基于A*算法的精确算法和启发式算法,在小规模问题上表现非常出色。
Roy等[15]开发了一个封闭排队网络模型。他们使用基于周转率分类的存储策略来估计机器人移动系统的订单吞吐时间。Lamballais等[16]扩展Roy等[15]的工作。通过推导分区时订单行程时间表达式,他们研究了一个半开放排队网络模型来估计平均订单周期时间和机器人、工作站的利用率。Yuan等[17]分析了一个开放排队网络来估计系统的总吞吐时间,计算出机器人的最佳数量和达到一定吞吐量所需的平均速度。Roy等[18]利用多类半开放排队网络对AVS/RS进行了性能分析,探讨了系统参数以及操作决策对性能指标的影响。由于半开放排队网络没有闭合表达式,他们设计了一种分解方法来评估系统性能。
综上所述,在网格紧致化存储系统的现有研究中,从系统区域划分的角度来分析系统效率的研究尚未展开。本文利用Yalcin等[13]的实验数据,分析基于网格的紧致化存储系统分区和ABC分类情况下对取货时间的影响。假设有外接快速传送带与各I/O点连接,在给定存储面积条件下将其分成几块小的区域,分析这种分区对响应速度的影响,也可以更好地利用现有算法在求解小规模问题上精度和速度的优势。另外,我们建立了排队网络模型对订单的平均等待时间和排队长度等绩效指标进行分析。
本文的其余部分安排如下:第1节介绍基于网格的紧致化存储系统;第2节构建系统分区和排队网络模型;第3节数值实验分析,最后是总结和展望。
1 系统描述
不失一般性,假设一个基于网格的紧致化存储系统是由方形传送模块构成的矩形网格(见图2),总长度为L,总宽度为W。每个模块是一个存储单元,可以在四个基本方向(上、下、左、右)上从一个位置移动到其相邻的位置。图中的灰色方块表示货物,白色方块表示未占用的存储位置(空位),黑色方块表示要取出的目标货物。

图2 基于拼图的存储系统俯视图(PBS)
在基于网格的紧致化存储系统中,一个订单到达并等待,直到它可以被分配到某一个I/O点。如图3所示,一旦订单被分配到一个I/O点,假设只有一个空位,首先需要将空位移到货物旁边,而后借用空位将货物移到I/O点,则完成取货,该订单将离开系统,然后下一个订单可以分配给该I/O点。当货物移动的下一个相邻位置被占用时,需要通过一系列空位与被占用的位置交换的方式移动到这个位置,因此,网格中必须有一个或多个空位可用。拼图策略的目的一般是最小化货物移动的次数。拥有更多的空位可以缩短取货时间,正如Gue[1]的研究结果表明,在密度不受限制的情况下,基于过道的系统是首选,但如果存储密度超过90%,则基于网格的存储系统是最优的。存储密度是专用存储空间与总存储空间之比,更高的存储密度意味着需要移动更多干扰货物,导致取货时间的增加,但却可以减少存储空间甚至总成本。排队模型可以将空位移动时间和订单等待时间等随机特性结合起来,估算出订单吞吐量、订单周期等性能指标。因此,有必要对空位数量、系统分区等因素对取货时间、排队时间等绩效的影响进行研究。
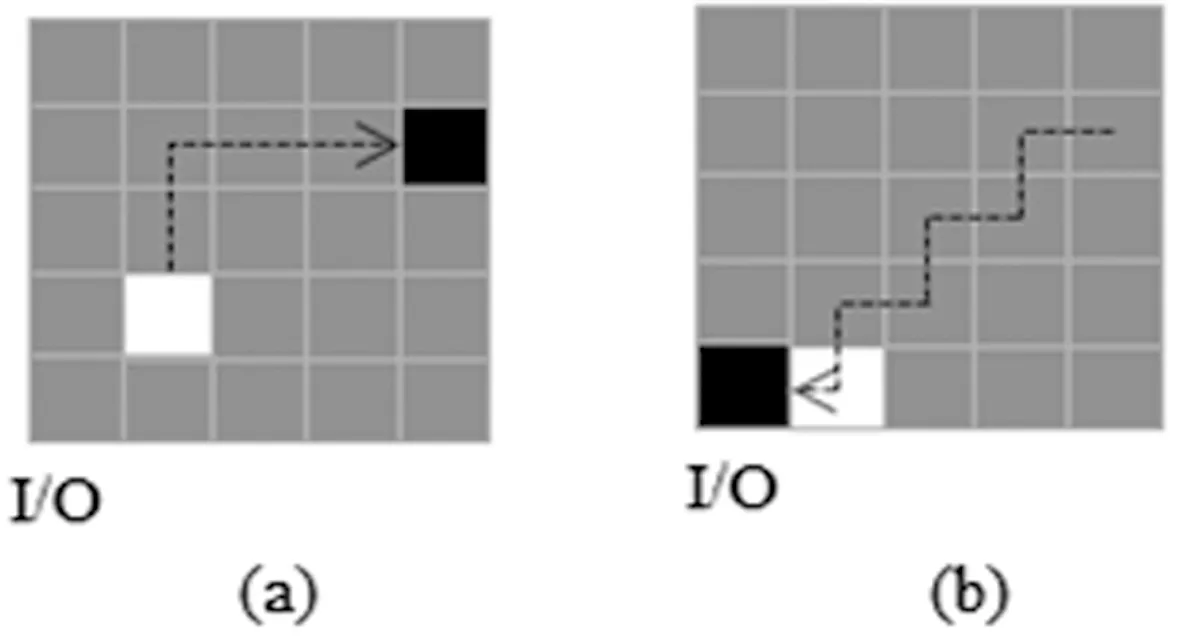
图3 取货移动步骤
论文做出以下假设:
1)系统内货物随机分布。对存储区实行分区或分类的情况,则分区或分类后货物在对应的区域内也是随机存储;
2)系统中有多个小区的情况下,不失一般性,假设I/O点位于每个小区域的左下角或左上角;
3)分区情况下,某一区内的空位不会移动到其他区域;
4)考虑在一个矩形的存储区中,一个位置最多只能被一个货物占用;
5)订单到达过程服从泊松分布。
2 模型构建
2.1 建模思路
基于网格的紧致化存储系统分区设计问题涉及要素多、情境复杂,难以精确量化,因此不易描述成数学规划模型,而排队网络方法能较好地处理这类问题。本文利用排队网络模型评估网格紧致化存储系统的性能和空位使用,这些模型可以描述网格紧致化存储系统中的取货过程,还可用于快速评估仓库布局或空位分布策略。假设需要将仓库存储区域分成s个小区域,就需要有s个I/O点独立工作。如图4所示,订单到达之后首先要排队等待;订单到达过程服从泊松分布,订单是逐个到达,且来源无限;提取每个订单货物所需的时间是独立的,订单服务时间由系统取货时间决定。若I/O点不忙,则在订单到达时直接执行服务;如果I/O点繁忙,则订单到来时排队等待。本文讨论系统若干参数的影响,例如货物数量、I/O点的数量、空位数量及分布等。另外使用三个指标来度量网格紧致化存储系统的性能,即排队长度、订单的等待时间和订单停留时间。队列长度包括系统中排队等待服务的订单数和接收服务的订单数。订单停留时间是订单等待时间和I/O点服务时间的总和。网格紧致化存储系统的分区模型由两部分构成,分别是:(1)基于取货时间的分区仓储子系统;(2)仓储分区内基于货物需求频率的ABC分类子系统。
2.2 分区模型
Yalcin等[13]基于A*算法设计了总能耗最小的精确算法,在不允许块移动条件下,总能耗最小的目标等同于时间最短的目标。他们在实验中给出了充足的最优取货时间数据,本文利用这些数据研究网格存储系统在不同面积情况下的分区布局问题,符号及其说明如表1所示。

图4 单队列:s个I/O点服务的并联排队系统

表1 符号及说明
2.2.1 基于取货时间的分区仓储子系统
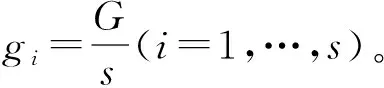

图5 基于取货时间的分区仓储子系统
2.2.2 仓储分区内基于货物需求频率的ABC分类子系统
根据ABC分类原理,需求频率高的产品存储在I/O点附近,而那些需求频率不高的产品存储在离I/O点远的地方,其主要目的是缩短取货时间。

图6 存储区分为三块区域的示例
在基于取货时间的分区仓储子系统基础上,再对已经分区的每个小区域根据订单需求频率对货物进行分类。根据Lamballais等[16]的研究,将系统分成3个区域,区域1大约占总存储区的20%,区域2大约占30%,区域3大约占50%。在同一行或同一列的位置上,对角线上的位置虽然距离I/O点较远,但容易进行3步移动的操作,而在偏离对角线的位置需要更多的5步移动操作,需要更长的移动时间,因此我们的分区形状是正方形而不是以I/O点为圆心的扇形,如图6所示。在分区仓储子系统中,每个存储区域都对应于ABC分区的某一分区,并根据产品的需求频率将产品分配到存储区域。PR是指订单所需产品刚好定位在R区范围内的概率。在任何存储区域中,空位都可以随机分布。货物也随机存放在相应区域。存储区域不重叠,因此所有存储区域一起覆盖整个存储区,多个空位可以同时位于同一存储区域。
2.3 排队网络模型
本文使用开放排队网络(OQN)模型,研究网格紧致化存储系统的排队长度、订单的等待时间和停留时间。在此模型中,每个订单都是单个独立抵达的,其订单相继抵达的时间间距遵从泊松分布。在订单排队过程中,我们从整个服务系统的角度来理解它的含义:队长不仅包括系统中等待服务的订单数量,还包括接收服务的订单数量。订单停留时间是系统中订单等待时间和服务时间的总和。订单等待时间是从订单进入系统到接受服务的时间段。相关参数及说明见表2。

表2 参数符号与说明
在基于取货时间的分区仓储子系统中,假设服务速率为ω,依照先到先服务的原则,订单进入系统,从I/O点受服务,空位根据订单的需求进行定位并取货,取货完成后订单离开系统。分区后的排队过程如图7所示。对于系统分区后进行ABC分类的排队模型,该模型总共包含R区。这意味着该模型包含R个服务站,每个存储区域一个服务站。如图8所示,ωR是表示拣取属于R区域目标货物的服务速率。
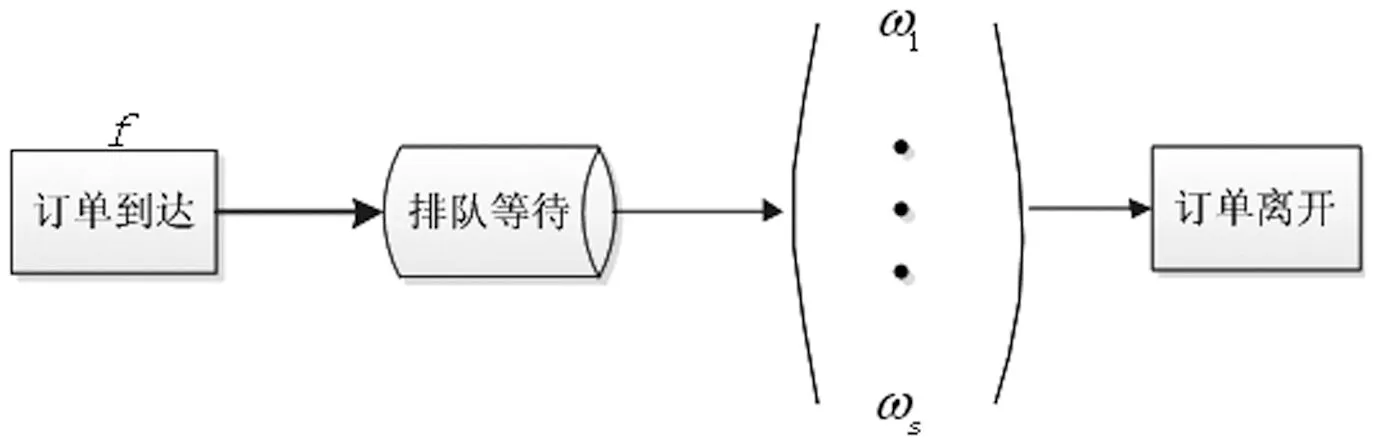
图7 分区的排队模型

图8 分区内的ABC分类排队模型
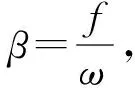
(1)
从订单进入系统,如果此时有闲暇的I/O点,则服务立刻开始,当服务完毕后I/O点再次变为闲暇状态,在此期间是I/O点忙碌的时间。根据唐应辉等[19]的研究,当βs<1时,其I/O点被占用的概率为
(2)
式(2)中,a代表订单数,当订单到达的数量少于I/O点的数量时,订单无需等待即可被服务;反之,如果订单的数量超过I/O点服务站数量时则订单需要排队等待,依照订单抵达的先后次序接受服务,其中P0是I/O点空闲的概率。
平均队长等于平均等待队长加正在被服务的订单数,因此其平均队长为
(3)
平均等待时间为
(4)
根据Little公式,由于订单的平均停留时间等于平均等待时间加上其I/O点服务的时间,即
(5)
3 数值实验分析
3.1 基于取货时间的分区分析
为了简要说明分区和分类对结果的影响,结合现有研究数据的可获得性,本文以10×10网格面积为实例,将其分成四个5×5的子网格区域进行分析。首先,根据Yalcin等[13]论文附录表Table A.1的数据,对空位数量和取货时间关系拟合如下:
10×10网格区域期望取货时间表达式:
E[q]=-0.00005q3+0.0129q2-1.2349q+58.245
(6)
5×5网格区域的期望取货时间表达式:
Em[q]=-0.00002q3+0.0052q2-0.5263q+26.702
(7)
根据关系式(6)和(7)可以绘制出期望取货时间和空位数量之间的关系(图9)。

图9 分区与不分区的期望取货时间比较
由图9容易看出,空位对取货时间的边际贡献是递减的,所以在小区的面积相等的情况下,空位尽可能在各小区内平均分布会使总的取货时间最短,也就是不同小区内空位数量的差不大于1。按此原则,将10×10网格区域分成5×5网格区域后,空位分配及期望取货时间如表3所示。其中,期望取货时间减少百分比v是使用随机存储分配规则作为基准,对比分区和不分区的差异,按公式(8)计算得到。
(8)

表3 10×10网格面积的分区结果
由表3和图9可知,分区与不分区的期望取货时间均随着空位数量的增加呈下降趋势,但下降速度递减。所有情形下,期望取货时间减少均超过50%,随着空位数量的增加,改善范围从52.1%到55.7%。分区后,虽然系统取货时间的改善程度也是空位数的增函数,但存储密度低于90%时是不符合网格紧致化存储系统定义的,故选用表3的第二行数据,即53.8%为说明分区后取货时间改善的依据。
3.2 分区内基于货物需求频率的ABC分类子系统订单队长与停留时间分析
在前述分区的基础上,即在10×10网格存储系统内划分四个5×5的小区域,每个小区域各设置1个I/O点。考虑将订单按需求频率分成A、B、C三类,相应地在每个小区内也根据储位到I/O点的期望移动成本划分成三个区域。具体分区方法是以I/O点为原点,2×2的区域为A区,3×3的区域去掉A区的部分是B区,其他区域为C区。
为了问题的简洁并不失一般性,假设货物每移动一步花费的时间为一秒。事实上,海康威视仓储机器人华域视觉项目已经落地[20],在武汉生产基地使用海康威视仓储机器人进行搬运货物的机器人移动一步的时间也在1秒左右。因此,如果每移动一步的时间是一秒,定义一分钟内系统能够完成的订单取货量为服务能力或服务率,由表4可以算出ABC分类的情境下不同的服务率。根据Hausman等[21]的研究,实验中ABC曲线通过函数G(i)=ik计算得出,其中k表示斜率。
定义ABC曲线斜率为1时的服务能力(服务率)为基本服务能力,那么每个小区的基本服务能力为2.75,系统中有四个小区,则总的基本服务能力为2.75×4=11。考虑到一般情况下系统的工作负荷(订单到达率)都会留有余地,首先我们观察订单到达率约为基本能力的50%的情况下排队系统的表现,取整为f=6,这时,实际订单到达率为基本能力的54.5%,是分区前服务能力的4.7倍。此时排队系统有4个服务站,用2.3节的排队网络模型计算结果见表4。

表4 仓储分区内三类存储策略的比较
表4中平均停留时间是平均等待时间与服务时间的总和,平均队长和平均停留时间由公式(3)、(5)计算得到。可见,系统的各项指标都随着ABC曲线斜率的降低而变好,其中,服务率最高可以提高46.5%,只要存在需求频率的差异,哪怕ABC曲线是20%~30%的情况,也有33.73%改善,可见ABC分类存储对PBS系统取货效率的改善幅度是很可观的。如果考虑到排队的作用,改善将会更大,最多可以达到72.34%。然后再观察其他几种订单到达率的情况对系统的影响,我们考虑到达率分别为基本能力的60%、80%、100%、120%,即订单到达率分别是6.6、8.8、11、13.2等四种情况,订单平均停留时间及停留时间的改进情况见图10。
与表4的结果类似,不同到达率的平均停留时间都随着ABC曲线斜率的降低而减少,平均停留时间改进百分比范围从19%至59%。可见,ABC分类后订单的平均停留时间都有不同程度的改善。对于20%~80%的ABC曲线,比分类前随机存储分配的改善都超过了52%。从图10(b)可以看出,随着到达率的增加,其ABC分类对系统的贡献逐渐减小。

图10 不同到达率下的平均停留时间趋势图(a)、平均停留时间改进百分比(b)
总之,仓储分区内的基于货物需求频率ABC分类子系统比基于取货时间的分区仓储子系统更有优势。因此,使用仓储分区内的基于货物需求频率ABC分类的方法明显降低订单的等待时间和停留时间、以及订单的排队长度。
4 结论和展望
本文研究了基于网格的紧致化存储系统的分区设计分析问题,讨论了PBS存储区域增加I/O点并划分小区以及小区内按ABC分类方法分区两种情况,并建立了开放排队网络模型,对系统的服务效率、顾客排队时间和停留时间等作业绩效进行了分析,主要有以下三个结论:
1)通过外接快速传送带的办法增加小区划分可以提高取货速度,因而能够提高系统服务能力。本文实验中将一个区域划分成4个小区,期望取货速度提高了53.8%;
2)根据帕雷托原理对小区进行ABC分类可以进一步提高系统服务能力,计算实验显示可以提高46.5%,平均订单停留时间最多可以缩短72.4%;
3)随着系统负荷(订单到达率)的增加,ABC分类对系统能力的提高效果会有所降低。
总之,对网格紧致化存储系统使用仓储分区内基于货物需求频率分类的设计方法能够显著提高系统的性能,可以为PBS系统在不同情境下的布局规划提供参考。
PBS系统分区和分类的研究对于推广PBS这一新型仓储系统的应用有重要的参考价值,仍有许多需要研究之处,未来的研究可以考虑从以下几点深入展开:首先是系统分区和快速传送带、PBS硬件等资源成本的对比关系研究,决定了系统总投资和运营成本,由于当前缺少数据支持,需要以后进行研究;其次,在问题建模方面,我们建立的是分析模型,而且假设小区之间不能共享空位,虽然结论也能够反映基本规律和正确的方向,但面对更具体的问题,松弛掉不能共享空位的假设并去掉小区边界限制,按照数字孪生的方法建立仿真模型会更加准确。

