具有工作站数量约束的多人工作站混合装配线平衡问题研究
赵文燕, 张世哲, 师柳柳
(河北工业大学 经济管理学院,天津 300401)
0 引言
多人工作站装配线平衡问题是客车、工程机械等大型产品生产线设计中的主要问题。目前多人工作站装配线平衡问题的研究多针对单一产品,通过建立单目标或多目标数学模型,利用启发式算法或智能算法求解,目标多为装配线总人数最小、工人负荷量均衡、各工作站装配不同产品所需时间的差异最小等。Dimitriadis首先研究了多人工作站装配线平衡问题,指出多人工作站装配线能够有效缩短装配线长度[1]。Chen等针对多人工作站资源受限装配线平衡问题,建立了以最小化工作站和工人数量为目标的优化模型,并采用混合遗传算法求解[2]。Fattahi等则在节拍已知条件下,以最小化人员数量为第一目标,最小化工作站数量为第二目标,设计了一种蚁群算法求解该问题[3]。Roshani和Giglio在工作站数量已知情况下,对以节拍和装配线总人数最小为目标的多人工作站单一产品装配线平衡问题利用模拟退火算法进行了求解[4]。童科娜等建立了以装配线节拍、工人数量以及工人负荷标准差最小为目标的多人工作站单一产品装配线平衡问题的数学模型,并设计了一种结构式译码遗传算法对该问题求解[5]。张梅等考虑工序复杂程度与工人能力差异情况,建立了以最小化工作站数量和工人数量为目标的优化模型,提出了一种改进的离散水波优化算法,并将其应用于动车装配线平衡优化中[6]。Zhang等以最小化工作站和操作员的总数为目标,采用模因蚁群算法求解了优化模型[7]。Yilmaz 建立了在给定周期内使工人数最小化的多人工作站装配线优化模型,采用禁忌搜索算法进行了求解[8]。
在多人工作站单一产品装配线平衡问题的基础上,学者们进一步研究了多人工作站混合装配线平衡问题。Roshani和Nezami[9]以工作站数量和装配线总人数最小为目标,利用模拟退火算法求解多人工作站混合装配线平衡问题。Kazemi和Sedighi[10]等则对以最小化生产成本为目标的多人工作站混合装配线平衡问题,利用遗传算法和粒子群算法进行了求解。国内学者针对多人工作站混合装配线平衡问题的研究还相对缺乏。
综上可知,现有多人工作站装配线的研究多以单一产品装配线为对象,混合装配线的研究要么以工作站数量为优化目标,要么对工作站数量不加限制。然而,多人工作站混合装配线设计或改造过程中,由于场地、成本等因素的影响,装配线工作站数量可能受限或不易变更。针对这一特点,本文研究具有工作站数量约束的多人工作站混合装配线平衡问题,在节拍已知情况下,以装配线人数最小、工人负荷量均衡、各工作站装配不同产品所需时间的差异最小为目标,建立相应的数学模型,并设计一种结合差分进化的多目标混合遗传算法对该问题求解。
1 模型建立
1.1 问题描述
设装配线生产NP种类型的产品,装配线共有NW个工作站,每个工作站最多容纳Mmax名工人,给定NP种产品的生产比例、作业要素标准时间、装配线节拍,在满足作业要素优先顺序的情况下,为每个工作站合理分配工人数量,并合理安排每个工人所需完成的作业要素及顺序,使装配线在所有工作站均被有效利用的条件下,达到以下三个目标:装配线总人数最小、装配线工人负荷量波动最小和各工作站装配各产品的装配时间波动最小。针对该问题做出如下假设:
(1)不同工人完成相同作业要素的时间相等。
(2)同样的装配作业需要分配至相同的工作站和工人。
(3)不考虑产品在工作站之间的搬运时间。
(4)不考虑产品切换时间。
(5)各工作站最大人数限制已知。
(6)工作站数量已知且需充分利用。
(7)每个作业要素只能由一个工人独立完成。
1.2 数学模型
本文模型中用到的符号定义如表1所示。
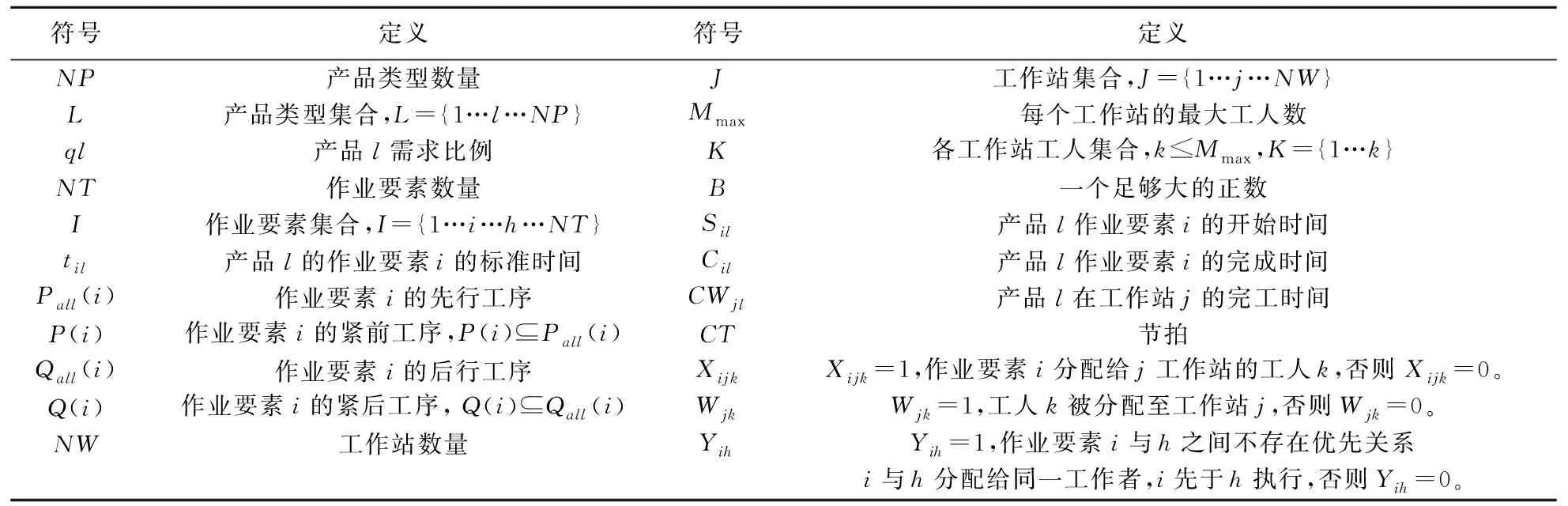
表1 符号定义
在多人工作站混合装配线平衡问题中,由于各品种在各个工序的工作时间不同,且工人在工作过程中可能存在等待现象,工人的完工时间并不能很好地描述其负荷量,因此将每个工人完成每种产品的有效工作时间的加权平均时间作为工人负荷量,因此,工作站j的工人k的负荷量为:
WLjk=∑i∈I∑l∈LqlXijktil
(1)
装配线总人数最小、工人负荷均衡、产品在各工作站的加工时间与节拍差值最小的具有工作站约束的多人工作站混合装配线平衡问题的数学模型为:
Objective min(∑j∈J∑k∈KWjk)
(2)
(3)
(4)
s.t.∑j∈J∑k∈KXijk=1,∀i∈I
(5)
(6)
∑k∈KWjk≥1,∀j∈J
(7)
(8)
∀i∈I,h∈P(i),∀j∈J
(9)
Shl-Sil+B(1-Xhjk)+B(1-Xijk)+B(1-Yih)≥til
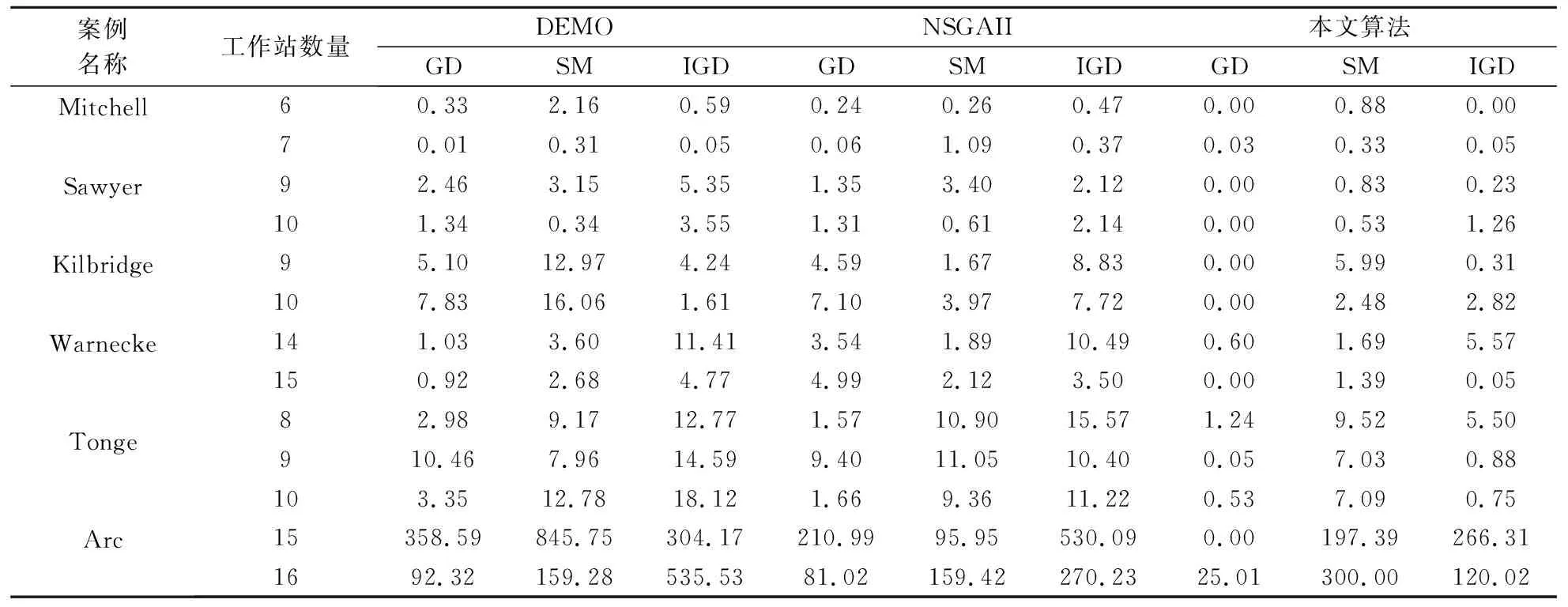
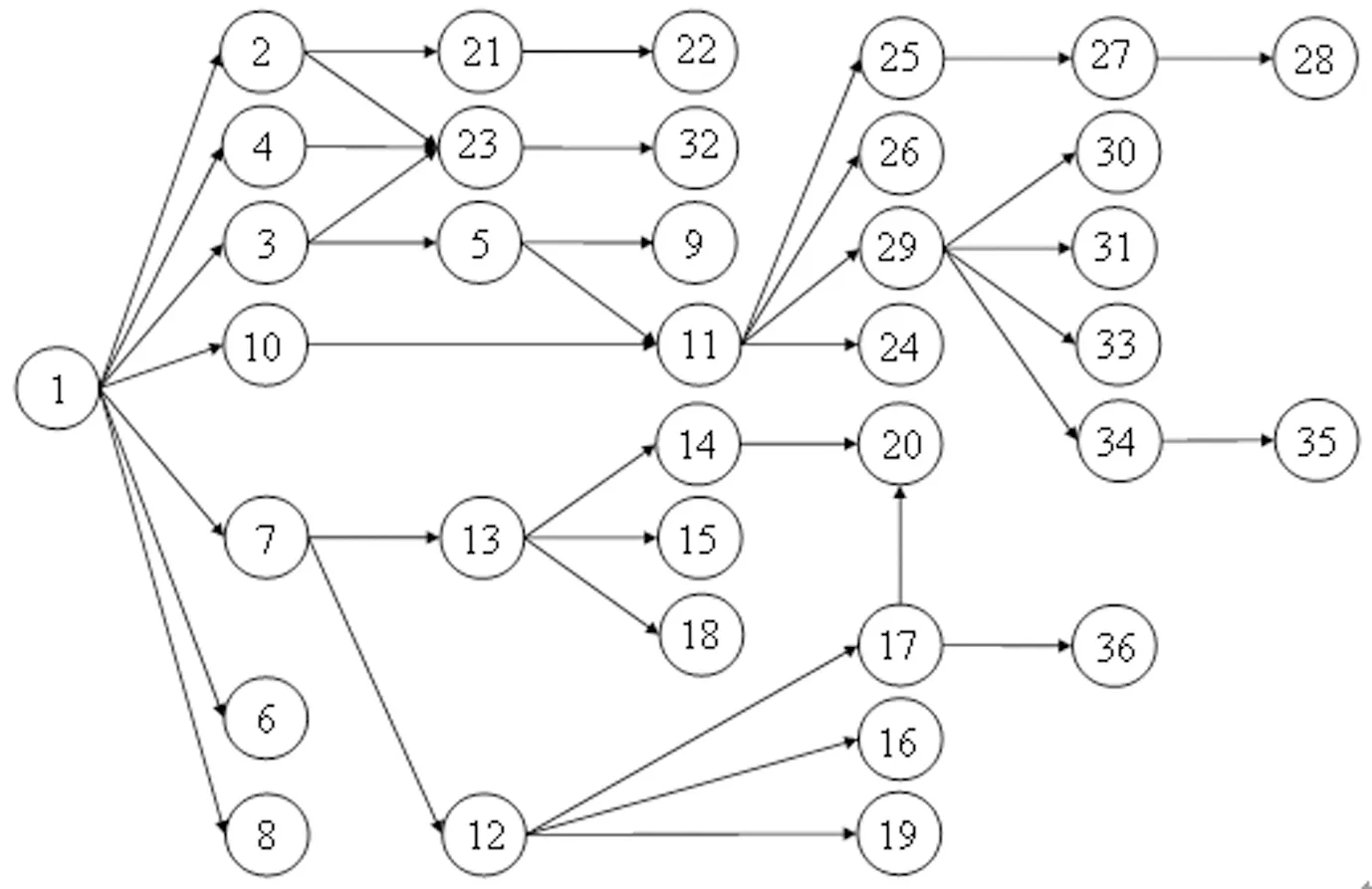
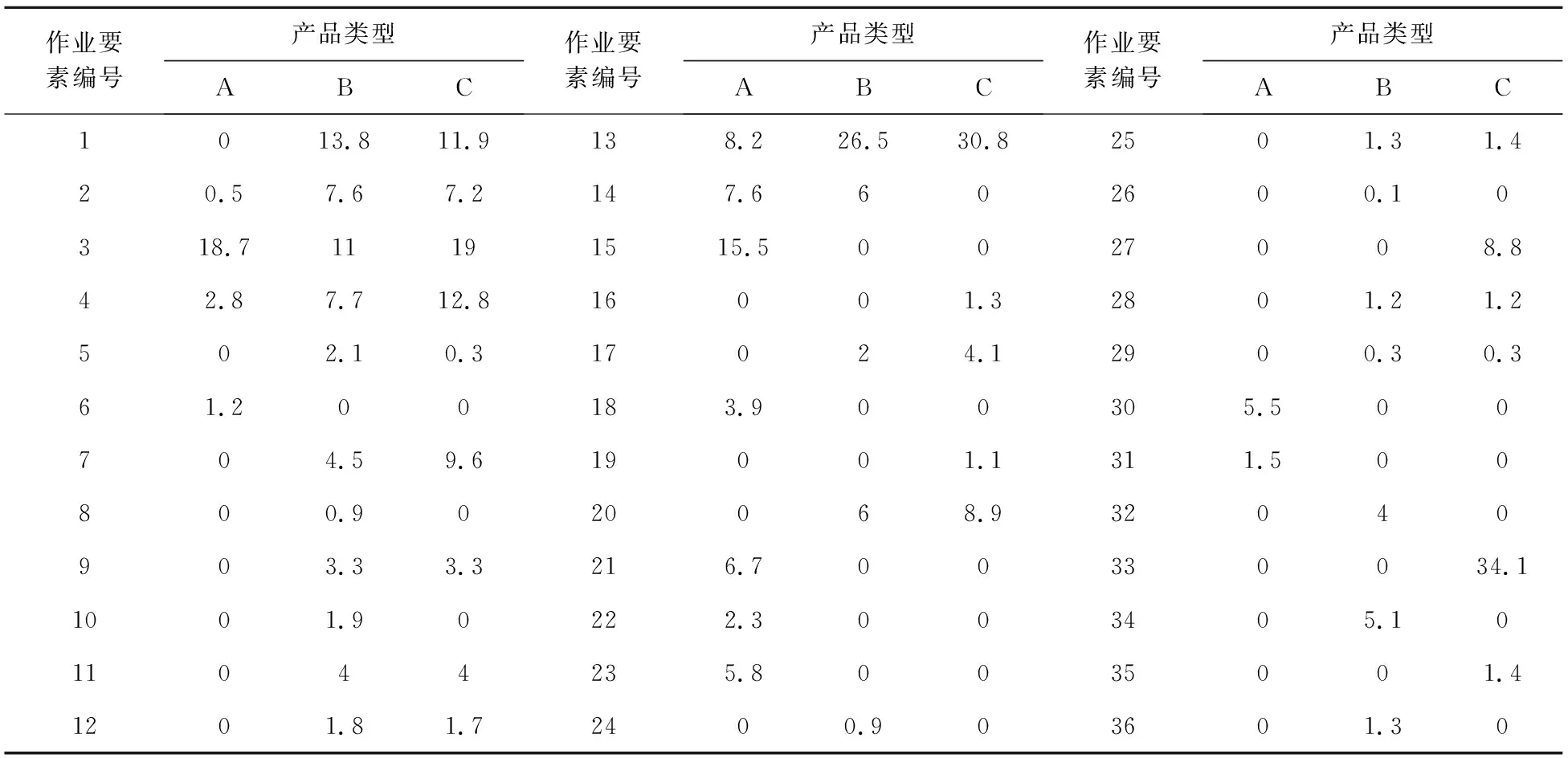
∀i∈I,h∈{r|r∈I-(Pall(i)∪Qall(i))andi ∀j∈J,∀k∈K,∀l∈L (10) Sil-Shl+B(1-Xhjk)+B(1-Xijk)+BYih≥thl ∀i∈I,h∈{r|r∈I-(Pall(i)∪Qall(i))andi ∀j∈J,∀k∈K,∀l∈L (11) (12) (13) Wj(k+1)≤Wjk,∀j∈J,∀k∈K,k (14) Sil+til≤Cil,∀i∈I,∀l∈L (15) (16) (17) 0≤Sil,∀i∈I (18) Xijk∈{0,1},∀i∈I,∀j∈J,∀k∈K (19) Wjk∈{0,1},∀j∈J,∀k∈K (20) Yih∈{0,1},∀i∈I,h∈{r|r∈I-(Pall(i)∪Qall(i))andi (21) 模型中,(2)~(4)分别表示三个目标函数:装配线总人数最小、工人负荷量标准差最小和各工作站各产品装配时间对于节拍的标准差之和最小;(5)表示每个作业要素只能被分配一次;(6)表示所有作业要素必须被分配;(7)表示每个工作站至少分配一个工人;(8)表示作业要素分配必须满足优先关系;(9)表示产品l的作业要素h为i的先行作业要素,当h与i分配在同一工作站时,i必须在h完成之后才能开始;(10)表示产品l的作业要素h与i不具备先行或者后行关系,作业要素i与h分配给同一工作站同一操作者,且作业要素i的操作顺序先于h,h必须在i完成之后才可开始;(11)表示产品l的作业要素h与i不具备先行或者后行关系,作业要素h与i分配在同一工作站同一操作者,且作业要素i完成顺序在h之后,i必须在h完成之后才可开始;(12)表示每个工人必须分配至少一个作业要素;(13)表示作业要素i分配给工作站j的工人k,则Wjk必须等于1;(14)表示各工作站工人按增序进行索引;(15)表示作业要素必须完成;(16)表示各作业要素的完成时间必须小于工作站总操作时间;(17)表示工作站平均装配时间满足节拍约束;(18)表示作业要素开始时间大于0;(19)~(21)分别表示变量X、W、Y的取值范围。 装配线平衡问题是一类典型的NP-hard问题,普通的精确算法难以进行求解。本文设计了一种多目标混合遗传算法用于求解本文多人工作站混合装配线平衡问题。 将染色体编码分为两部分,前者对应作业要素的分配顺序,后者对应每个工作站分配的工人数量,染色体采用随机键编码的方式,编码长度分别为作业要素数量和工作站数量,为每个作业要素分配一个0到1之间的随机数作,为每个工作站分配一个0到最大工人数Mmax之间的随机数。 在编码得到染色体后,进行解码得到装配线配置方案。设工作站j的工人集合为Kj;工作站j中工人k完成作业要素i后,工作站的平均装配时间为tijk;装配线节拍为CT。解码步骤如下: Step1令j=1。 Step2对工作站j人员分配部分编码向上取整,得到工作站j的人员分配。若取整后工作站人数大于Mmax,则将工作站人数设置为Mmax;若取整后工作站人数小于1,则将工作站人数设置为1。 Step3找出无紧前作业要素或紧前作业要素已分配的作业要素作为可选作业要素集A,从可选作业要素集中选出权重最大的作业要素作为待分配作业要素,若权重最大的作业要素有多个,则随机选择一个,设该作业要素为i。 Step4计算工作站j内工人k完成作业要素i后工作站j的平均完工时间tijk,∀k∈K。 Step5若min(tijk)≤CT(∀k∈K)则将作业要素i分配给min(tijk)所对应的工人,若min(tijk)所对应的工人有多个,则将作业要素i随机分配给其中一个工人, 并转Step 7。 Step6若min(tijk)>CT(∀k∈K),则工作站j分配完毕。若所有工作站分配完毕,则退出,否则,令j=j+1,转Step2对工作站j=j+1进行分配。 Step7判断作业要素是否分配完毕,若分配完毕,则结束,否则,转Step3继续分配。 经解码后的种群(染色体个数为N),其染色体可能会两种不符合约束的情况:(1)作业要素无法全部分配,(2)工人或工作站未利用。对情况1所对的应染色体,采用罚函数法进行处理;情况2所对应染色体将产生较大的目标函数值。这两部分个体将会在之后的更新中被淘汰。 设种群中的染色体x的第i个目标函数值为fi(x)(i=1,2,…,p),fi(x)∈f(x)。若两个染色体x1和x2的目标函数值均有fi(x1)≤fi(x2),其中只要任意一个fi(x1) 按照f(x)对种群排序,最优的染色体排到第1层,次优的排到第2层,依次进行。若同层有多条染色体,则需计算各染色体的拥挤度。根据每个目标函数对种群中的所有个体按升序进行排序。将同层两个边界染色体的拥挤度设为无穷大,第i个个体的拥挤度则设为第i+1和第i-1个体的所有目标函数值之差的和。在之前分层排序的基础上,对同层内染色体按照拥挤度由高到低排序,完成种群内染色体的排序。 采用联赛选择算法,从种群中随机选择m条染色体形成交配池,要求m≤N/2。本文采用的基本方式是随机从种群中选择两条染色体,将排序层次低的染色体放入交配池,当两条染色体处于同一层时,选择拥挤度较大的染色体放入交配池。重复进行,直到形成m条染色体的交配池。 在进行交叉操作时,按交叉概率分别对作业要素排序和工作站人员进行两点交叉。在完成交叉操作后,按照变异概率,任选一个作业要素重新为其分配一个0到1之间的权重,随机选择一个工作站重新为其分配一个0到Mmax之间的随机数。经交叉变异形成m条子代染色体后,与原种群中排序最后的m个染色体共同组成染色体集Y,对该集合按照2.2节的规则排序,取最优的m条染色体遗传至下一代。 由于遗传算法局部搜索能力较弱,为解决这一问题,本文将差分进化操作嵌入遗传算法,以增强遗传算法的局部搜索能力。算法对种群中最优的k条染色体进行差分进化操作,其中k≤N/2,其步骤为: Step1从排序的种群中,选择前k条染色体进行差分进化。 Step2设k条染色体组成染色体集为X,当前进行差分进化操作的染色体为Xl,随机从染色体集X中选择3条染色体:Xa、Xb、Xc,其中l≠a≠b≠c,借助缩放因子F得到变异染色体Hl,其公式为: Hl=Xa+F×(Xb-Xc) (22) Step3对染色体Xl进行交叉操作生成新染色体Ul。设染色体长度为D,则Xl={Xl,1,Xl,2,…,Xl,D},Hl={Hl,1,Hl,2,…,Hl,D},则新染色体Ul={Ul,1,Ul,2,…,Ul,D}按如下规则确定: (23) 式中,CR为交叉概率,drand为染色体中随机选择的一个基因。所有Ul共同构成染色体集合U。 Step4染色体集U与染色体集X合并形成染色体集Z,对Z排序后选择最优的k条染色体替换染色体集X遗传至下一代。 本文设计的结合差分进化的多目标混合遗传算法流程图如图1所示。本算法既借助遗传算法保持样本多样性,又借助差分进化操作加快优化速度,进而快速获得全局最优。 图1 算法流程图 将本文算法与DEMO[11]、NSGAII[12]和Roshani和Nezami在文献[9]中提出的算法进行对比。用MATLAB编写算法程序,在配置为Intel Core i5-7300HQ CPU、8.00GB RAM的PC上运算。 选用10个装配线平衡案例进行实验,其中作业要素数7~10的小规模问题案例4个,作业要素数21~58的中等规模问题案例4个,作业要素数70以上的大规模问题案例2个。作业要素优先关系可以从www.assembly-line-balancing.de下载。由于这些案例的原问题均为单一品种装配线平衡问题,因此,对案例稍加更改。根据文献[9],保持这些案例的作业要素优先顺序不变,将作业要素时间设置为0到原案例中最大作业要素时间之间的随机值,工作站最大工人数设置为2,产品类型数量设置为2,各产品比例均设置为0.5。各算例相关信息如表2所示。 表2 案例相关信息 表3中LBw表示装配线理论最小人数,其计算公式为: (24) 式中,「 ⎤表示向上取整。 在进行比较之前,以案例9为例,以IGD[13]反世代距离为指标对各算法进行参数效验,各算法参数组合与最优参数如表3所示,本文遗传算法信噪比主效应图如图2所示。 表3 算法参数组合与最优参数 图2 信噪比主效应图 在本文算法与DEMO、NSGAII进行对比时,采用世代距离GD[14]、空间评价指标SM[15]、反世代距离IGD分别作为算法收敛性、均匀性、综合性评价指标,其计算公式如式(25)(26)(27)所示。 (25) 式中,n为算法所得到解集中解的数量,di为算法所得到解中个体与参考集中最近解之间的欧几里得距离。 (26) (27) 式中,P为参考解集,Q为算法求得的解集,d(v,Q)为解v与Q中最近的解的欧氏距离。 将三种算法所求得全部解中的非劣解集作为GD与IGD中的参考集,每种算法运行3次取最终得到的非劣解进行计算。由于案例1~4三种算法所得到结果一致,因此仅展示案例5~10的计算结果,如表4所示。由表4中信息可知,本文遗传算法的GD以及IGD明显优于DEMO以及NSGAII,这说明本文算法的收敛性以及综合性能明显优于另外两种算法。在解集均匀性方面,本文算法分别有9个案例中的SM小于DEMO和NSGAII,因此,本文算法在均匀性方面也优于DEMO和NSGAII。 表4 计算结果 将本文算法与文献[9]算法进行比较,两种算法每个案例运行3次,取最优结果和平均CPU时间。本文算法中各工作站数量均设置为文献[9]算法计算后所得工作站数量,在本文算法得到的非劣解中,按照工人数最少、工人负荷标准差最低和各工作站产品装配时间标准差之和最小的顺序选择一个方案对比,得到的结果如表5所示。其中,Ns表示工作站数量,Nw表示工人人数,DL表示工人负荷量标准差,DT表示各产品各工作站装配时间与节拍标准差之和,CPU表示CPU时间。 由表5可知,除Jaeschke和Jackson两个案例外,其他案例中本文算法得到的工人数量均小于文献[9]算法,在工人数量相同的情况下,得到工人负荷标准差也优于文献[9]算法。在运行速度上,两种算法在小规模问题上相差不大,随着问题规模的扩大,本文算法明显优于文献[9]算法。 表5 测试结果对比 某挖掘机上车架混流装配线共226个作业元素,A、B和C三种产品,产品比例为3:5:2,装配线共12个工作站,每个工作站最大人数为5,原装配线节拍为88min,装配线总人数为18,工人负荷量标准差约为14.43。为满足不断增加的客户需求,新的装配线节拍设置为52min。经本文算法优化,在满足节拍约束,保持现有工作站数量的情况下,装配线总人数由18人减少至16人,工人负荷量标准差由14.43减少至5.67左右。限于篇幅,此处仅给出挖掘机部分线路装配线平衡过程和结果。 挖掘机线路装配过程共包含36个作业要素,作业要素综合优先顺序如图3所示,作业要素标准时间如表6所示。设定2个工作站,在节拍52min和各工作站最大工人数5的限制下,经本文算法优化得多个优化方案,其中一个优化方案如表7所示。两个工作站共需3个工人,其中工作站1工人数为2,工作站2工人数为1,装配线工人负荷量标准差为4.49。 图3 作业要素优先顺序 表6 作业要素标准时间 表7 计算结果 针对装配线设计或改造过程中,节拍已知条件下,工作站数量存在约束的多目标多人工作站混合装配线平衡问题进行研究,建立了数学模型,并设计了一种结合差分进化算法的多目标遗传算法进行求解。实验结果表明,本文算法的计算结果在收敛性、综合性能方面明显优于DEMO、NSGAII,在均匀性上略优于DEMO、NSGAII,另外,本文算法所得到的解在装配线人数最小以及工人负荷标准差最低方面明显低于Roshani和Nezami在文献[9]中提出的算法,这也为企业更好解决类似装配线问题提供了理论基础以及相关方法。但是,本文未考虑装配线调整过程中将会出现的各项成本,这也是未来的研究中需要解决的问题之一。2 混合遗传算法设计
2.1 编码与解码
2.2 排序以及拥挤度计算
2.3 选择
2.4 交叉和变异
2.5 差分进化
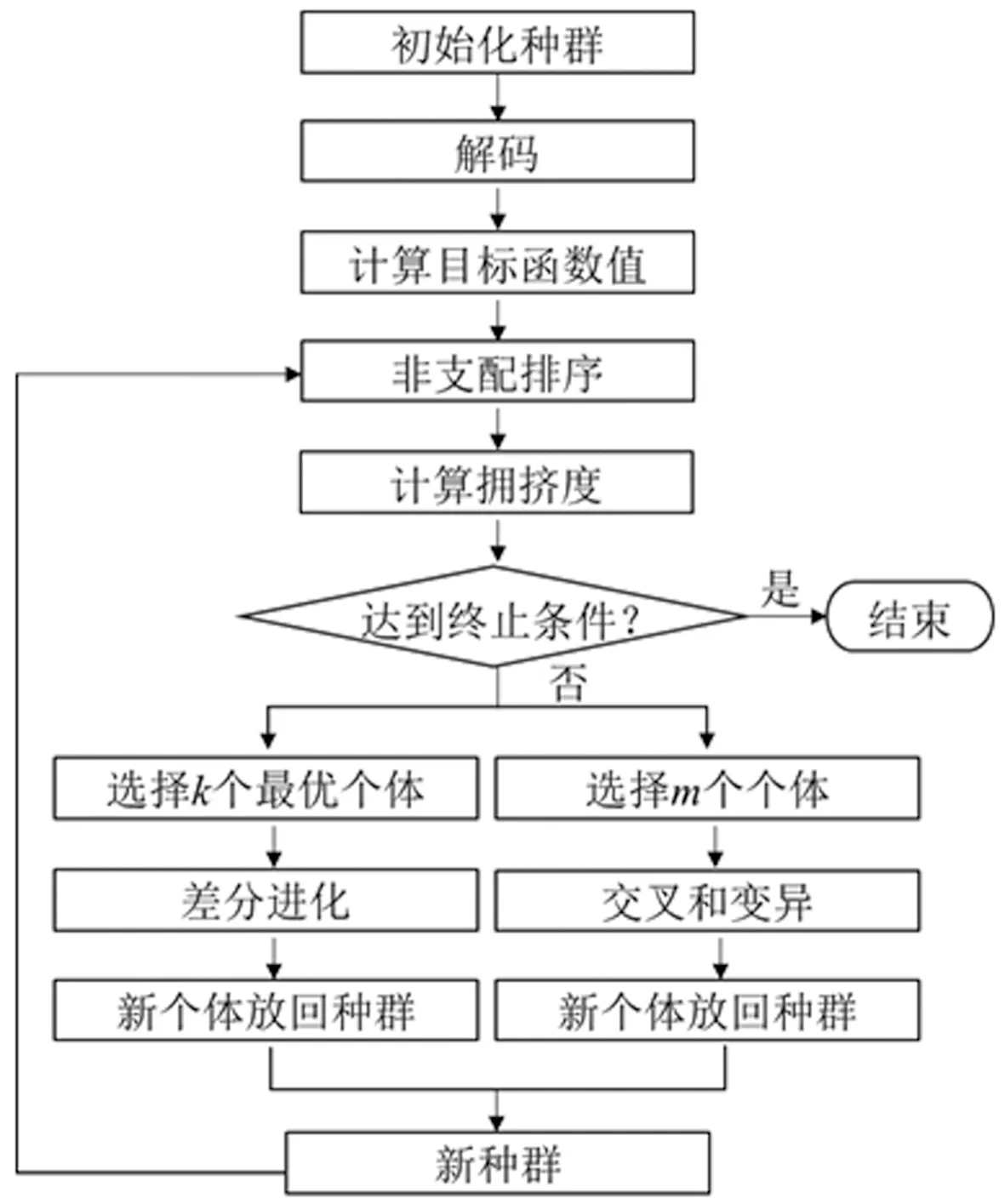
3 数值计算
3.1 参数效验
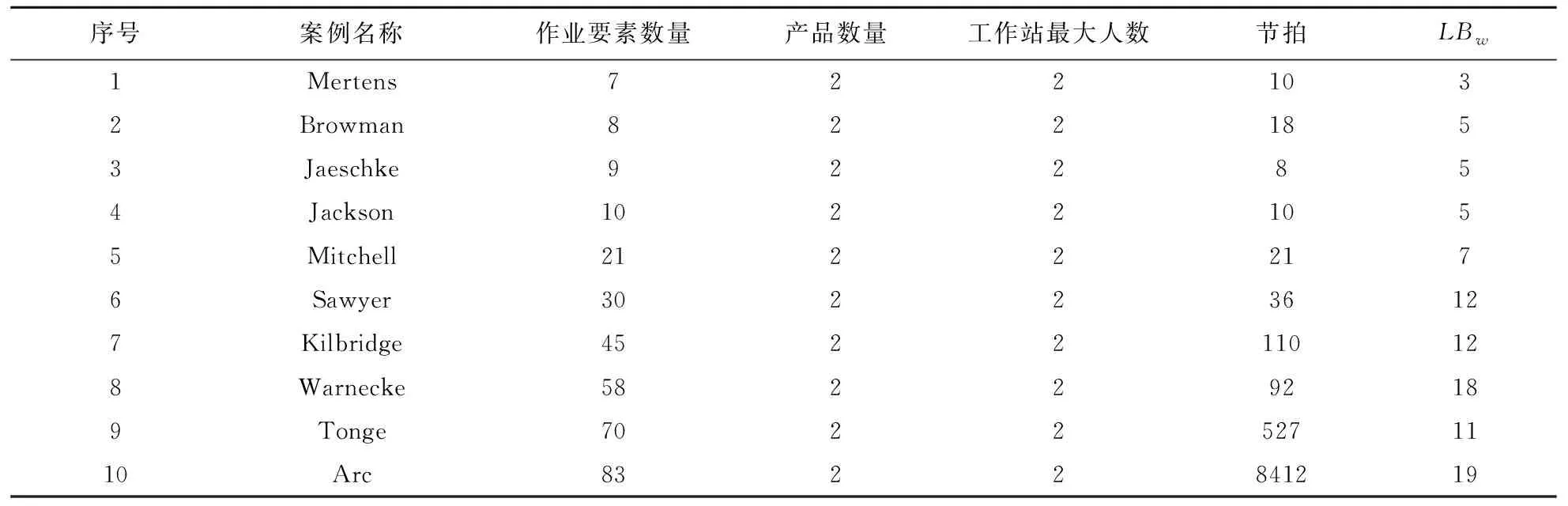

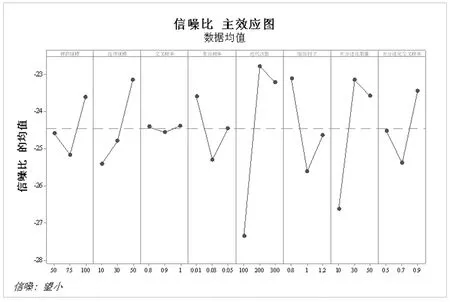
3.2 方法对比分析
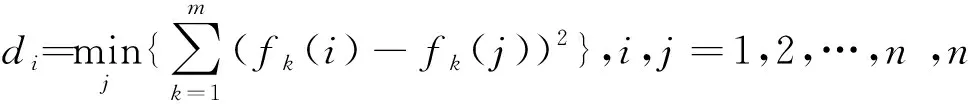

3.3 实例计算

4 结论

