变风量空调系统房间温度控制研究
杨世忠,李善伟,于瀚博
(青岛理工大学信息与控制工程学院,山东 青岛 266520)
1 引言
变风量(Variable Air Volume, VAV)空调系统在能耗、舒适性等方面存在很多明显优势,因而在空调系统设计中占据很大市场,但其系统在实际控制中由于存在自身非线性、时变性等问题,难以建立精确的数学模型。众多研究表明,针对此类系统,模糊PID控制能取得较好效果,具有不错的鲁棒性。但是在实际的控制过程中,随着控制过程的进行,控制系统的输出误差越来越小,模糊论域却固定不变,使得模糊划分变得粗糙,而模糊控制在变量分级不够的情况下,控制精度无法满足控制要求。
针对模糊PID控制算法存在的以上问题,引入变论域思想,提出了一种变论域模糊PID控制方案,并且通过细致分析误差变化过程中对论域模糊规则的要求以及伸缩因子对论域变化的影响规律这两大方面,设计出一种改进型输入端伸缩因子,使得控制过程在模糊规则数量不变的前提下,通过设计的伸缩因子来调节论域范围,论域变化相当于模糊规则数量的变化,从而提高了控制精度,保证了系统的稳定性。
2 VAV空调室温控制系统
2.1 变风量空调房间温度控制原理
变风量中央空调系统以调节区域的温度变化作为控制信号,通过VAVBOX对送风量进行自动调节使房间温度维持在设定范围内。改变送风量是通过调节末端风阀开度大小实现的。本实验平台采用压力无关型VAVBOX,其控制回路如图1。

图1 压力无关型VAVBOX控制回路
控制方式采用双闭环串级控制,主环为温度控制环,副环为风量控制环。通过对主副环的输入和输出值进行相应处理,从而对风阀开度进行调节,实现房间温度调节。
2.2 “VAV风阀开度-送风量”模型建立
本文基于LabVIEW软件采集到的输入输出数据的基础上,通过系统辨识的方法确定该被控对象的控制模型。分为下列4个步骤:
第一步:确定“风阀开度-送风量”变化的线性范围。由于实验平台本身原因,风阀开度设置在20以下检测不到风量,因此设置风阀开度范围为20-100。程序运行结果如图2所示。由图2可知,风阀开度变化会导致送风量随之改变,其线性区间为30-80.

图2 送风量随风阀开度变化的特性曲线
第二步:通过“风阀开度-送风量”阶跃响应测试,确定系统的延迟时间和调节时间。通过第一步所确定的线性区间,加载开度40-50的阶跃信号,实验结果如图3所示,由图中数据分析可知延迟时间约为4s,调节时间约为13s。

图3 风阀开度-送风量阶跃响应
第三步:输入幅值不变,对风阀开度控制端加载正弦信号,观察送风量的变化情况,确定系统的截止频率。结果如图4所示。

图4 加载正弦信号求截止频率
调整正弦信号的频率为0.01Hz时,送风量输出幅值基本没有发生变化,确定基准幅值为46m3/h,频率变为0.05Hz时,幅值为36.1m3/h,约为基准值的78%。确定系统截止频率为0.05Hz。
第四步:加载M序列信号,采集辨识所需要的数据,导入到MATLAB/Ident工具箱中所得图像如图5。其中M序列采样时间、采样周期、阶次各参数由公式计算可得,Δt=3s;Np=5s;n=3。

图5 加载M序列运行结果
经系统辨识,并对拟合出的模型进行相应处理,以方便控制器设计,得出VAVBOX风阀开度-送风量数学模型为

(1)
房间模型可以通过能量守恒定律,并查实验室变风量空调实验手册,获得各参数数据,进行数学模型建立。
3 变论域自适应模糊
3.1 变论域模糊原理
一般来说,模糊控制器的论域范围在模糊规则设计完成后都是固定不变的。随着控制过程的进行,控制系统的输出误差越来越小,在输入论域本身任何没有变化的前提下,不断变小的误差就使得模糊划分变得相对粗糙,模糊规则对输出参数的调节作用变小,控制效果变差。从数学角度对模糊控制器进行分析可知,模糊控制模型的实质基本都是某种插值函数,模糊集合即为插值的基函数。由插值得到的控制函数对真实控制函数的逼近程度越高,那么控制精度越高,而逼近程度就是模糊集峰点之间的距离所决定,峰点间距离与逼近程度成反比。因此若想要控制器精度变得足够高,就要使模糊集峰点的距离缩短,即模糊规则划分更加细致,大量增加模糊控制规则,实际操作中无法实现。于是引入变论域思想:通过引入论域伸缩因子,使得论域随着误差变化而发生改变,即误差变小,论域收缩,误差变大,论域膨胀,但控制规则未发生变化,从另一角度看,相当于是对模糊控制规则的补充,控制精度随即提高。
对于输入变量x和输出变量y,设其初始论域分别为X=[-E,E]和Y=[-U,U]。A={Ai}、B={Bi}(1 IfxisAi,thenyisBi, 设xi、yi表示Ai与Bi的模糊集峰点,那么模糊控制器就可以用如下插值函数进行表示 (2) 引入论域伸缩因子,变量的初始论域变换为[-α(x)E,α(x)E]和[-β(y)U,β(y)U],其中α(x)和β(y)分别是输入论域和输出论域的伸缩因子,输入变量与输出变量所对应的模糊推理论域分别为[-N,N],[-M,M]。变论域模糊控制器可用如下函数进行表示 (3) 其中x(t)(x(t))T. 在引入变论域思想后,输入变量的量化因子与输出变量的比例因子两者的关系改变为 (4) (5) 论域的变化可以与Kx、Ky相结合,使得变论域思想在实际控制中得到更好的理解与应用,量化因子与比例因子的取值发生改变时,论域在某种角度来看也会发生相应的变化。误差不断缩小,如果量化因子不变,那么此时的论域范围相对模糊控制器的输入模糊量而言过大,控模糊规则划分过于粗糙,所使用的控制规则数量减少,调节作用减弱,因此要增大量化因子,使论域范围相对于输入模糊量而言进行压缩。同理,减少比例因子,使论域范围对输出量而言进行压缩。结合上式可以得出变论域模糊控制在应用中,只需将输入变量的量化因子与输入变量对应的伸缩因子相除,输出变量的比例因子与输出变量对应的伸缩因子相乘即可。 图6 论域压缩与膨胀 在研究误差变化的过程中,详细分析伸缩因子对论域伸缩的控制作用,从而将误差变化与伸缩因子变化的规律总结如下: 在误差较大时,模糊控制规则无需进行细致的划分,采用粗略的控制规则,规则不需要增加,即论域不用进行伸缩或膨胀,伸缩因子变化速度缓慢。在误差中等时,粗略的控制规则控制效果不佳,不再适用,需要将控制规则进行细化,论域进行适当缩小,伸缩因子变化速度中等。当误差向零逼近时,需要模糊划分更为精细的控制规则,因此伸缩因子变化速度较快,论域快速收缩,使得在此误差范围内,控制器的模糊控制规则数量快速增加,消除误差。 优化准则推导如下: 通过以上分析,在输入端指数函数型伸缩因子的基础上,根据增量法来确定一种改进型伸缩因子,由于Δx与Δα成正比,当任意给出一个增量Δx,对应一个增量Δα。同时,由上述总结的伸缩因子变化规律可以得出,对相同的增量Δx,当x越大时,Δα应越小,因此有 Δα=k×Δx×(1-α)×(E-|x|)/E (6) 求解方程可以得出: α(x)=1-λe-k1|x|+k2x2 (7) 其中k1>0,k2>0,λ>0,α(x)的取值范围为(0,1),且k1、k2和λ的取值在一定程度上反应了系统控制的灵敏度与精度,需要综合考虑系统的各项性能指标。该式便是根据伸缩因子优化推导准则所得出得改进函数型伸缩因子表达式,从式(7)中可以看出存在三个可调参数,所以在线调整时灵活性更大。 变论域模糊PID控制器的结构如图7所示。该系统选用变风量空调房间温度与温度设定值的偏差e和偏差变化率ec作为输入,选取PID参数增量ΔKP、ΔKi、ΔKd作为模糊控制器的输出量。 图7 控制系统整体结构图 由于输入量和输出量均为精确量,因此设其模糊语言变量分别为E、EC、KP、Ki、Kd,选取语言值NB、NM、NS、ZO、PS、PM、PB对这些量进行模糊化。 参照PID三参数在控制过程中实现的作用,以ΔKP为例建立模糊控制规则表见表1。 表1 ΔKp模糊控制规则表 设各个变量的初始论域分别是:Ue0=[-Ee0,Ee0],Uec0=[-Eec0,Eec0],Uk0=[-Ek0,Ek0](k=Δkp,Δki,Δkd),实际论域变为:Ue=[-Ee,Ee],Uec=[-Eec,Eec],Uk=[-Ek,Ek]。 采用变论域思想,即引入上述提出的伸缩因子,因此初始论域与实际论域的关系为:Ue=α(e)Ue0,Uec=α(ec)Uec0,Uk=β(k)Uk0(k=Δkp,Δki,Δkd)。 输入端伸缩因子 (8) 输出端伸缩因子 (9) PID控制器参数初值KP0、Ki0、Kd0的初值可用临界比例带法确定。于是PID控制器各参数的修正量为 (10) 为验证本文所提控制策略的优势所在,使用Matlab/simulink模块搭建仿真模型,房间温度设定值分别为19℃与21℃,送风温度设定为13℃,房间体积为39m3。 图8 VAVBOX变论域模糊控制仿真框图 图9 变论域模糊PID封装模块 图10 伸缩因子α(e)封装模块 图11 伸缩因子β1封装模块 对本文所提控制方法与常规模糊PID控制进行仿真,为保证算法对比的优势所在,整个过程中内环与外环采用相同的KP,Ki,Kd初始参数值。 表2 仿真控制器参数 图12 常规模糊作用下的房间温度曲线 图13 变论域模糊作用下的房间温度曲线 通过仿真曲线可以看出,在温度调节过程中,经过改进的变论域模糊PID算法控制效果明显优于模糊PID控制,具体表现为:调节速度快,且超调量小,房间温度实际值基本维持在设定值附近且波动范围小,并且当房间温度设定值发生变化时,变论域模糊PID初始阶段具有很快的上升速度,具有较好的动态性能。 为进一步验证所提控制策略的实际控制效果,在2020年7月10日到13日选取天气情况相差不大的两天的10:00-13:00时间段,通过LabVIEW软件模块化编程,将变论域模糊PID控制器与传统模糊PID控制器分别应用到变风量空调实验平台。 图14 变风量空调实验平台 图15 变风量空调系统智能控制柜 在基本相同的条件下,模糊PID控制器与变论域模糊PID控制器下的房间温度变化曲线如图16、17所示: 图16 常规模糊作用下的房间温度曲线 图17 变论域模糊作用下的房间温度曲线 通过温度曲线对比可以得出,实验结果与仿真结果基本走向一致,可以确定本文所搭建仿真模型的合理性。并且证明本文所提控制方法的可行性。 针对变风量空调系统中存在的时变性,非线性等特点,为了提高系统的稳定性及控制精度,本设计提出了串级变论域模糊PID控制器,细致分析误差变化过程中对论域模糊规则的要求以及伸缩因子对论域变化的影响规律,从而对原有的伸缩因子进行改进,改进后的伸缩因子能够使得论域变化速度更快,且不会出现跳变,能够使论域变化过程更加平滑,从而实现在不用增加模糊控制规则的前提下,使论域随误差变化而发生变化,提高了控制器精度。最终通过仿真与实验结果证明:在变风量空调系统温度控制过程中,相较于传统模糊PID算法,采用变论域思想的模糊PID控制器能够使得房间温度调节迅速,温度波动小,充分验证了控制策略的优越性,为变风量空调温度控制提供一种可行性的方案。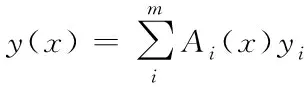




3.2 伸缩因子优化准则




4 变论域模糊PID控制器设计





5 系统仿真与实验
5.1 仿真研究







5.2 平台实验




6 结语

