点融合进近模式下的多机协同优化排序方法

魏志强，曹 格

(中国民航大学空中交通管理学院，天津 300300)

1 引言

随着民航运输业的持续、快速发展，终端区的进离场繁忙程度越来越高。欧洲控制试验中心提出点融合技术可提高多机运行效率并且降低管制员的工作负荷[1]。传统终端区进场模式下，Beasley等对飞机进场排序问题进行了研究，并建立了整数线性规划模型利用树搜索法对该模型进行了优化求解[2]；魏志强等研究了基于连续下降运行方式的下降阶段飞机性能参数计算模型，并数据拟合分析了该模型的影响参数[3]；谷润平等建立了基于到达时间约束下的连续下降进场模型，并通过精英保留的遗传算法求解，降低了飞机在终端区进场中的燃油消耗[4]；谷润平等对单架飞机多航路点到达时间约束的飞机性能参数进行了优化并预测了单架飞机飞行轨迹[5]；魏志强等对多条航路上飞行下降至同一航路点多架飞机的总运行成本进行了优化研究，建立了考虑间隔约束的参数优化模型，并通过遗传算法对其求解[6]。点融合技术进场模型下，Favennec等研究了高密度交通负荷下，点融合进近模式在人员配置、可预测性和环境等方面对特定终端区空域的适应程度[7]；Bruno等对现有技术相互协调作用和改进终端区航班到达流进行了描述，研究表明点融合进近模式可以解决高密度终端区航班拥挤问题[8]；邹朝忠等对比分析了传统终端区进场模式和点融合进近模式，并介绍了点融合进近模式的运行原则、运行优点和应用前景[9]；晁绵博等结合管制间隔要求针对长沙黄花国际机场设计点融合进近程序，并分析了其静态容量[10]；赵向领等对长沙黄花国际机场点融合技术的近地风险给出评估方法[11]。

以上研究介绍了点融合进近模式的结构特性、飞机在传统进场模式的排序问题和飞机性能参数的计算方法，但未将点融合进近模式与飞机性能结合研究多架飞机协同进场的飞行航迹及排序优化问题。本文在考虑飞机性能的基础上，首先介绍点融合进近4D航迹预测模型；其次优化点融合进近模式多机协同进场排序，提高飞行效率和降低运行成本。

2 基于点融和进近模式的多机排序优化模型

2.1 点融合进近模式结构描述模型

点融合进近模式的进场分为三个飞行阶段：阶段1，排序边飞行阶段；阶段2，直飞融合点阶段；阶段3，下降飞行阶段。经典的点融合进近模式如图1，其中弧AB为外排序边；弧CD为内排序边；航路点E为直飞融合点时飞机所处的位置；航路点F为开始下降时飞机所处的位置；航路点G为融合点；θ为汇聚角；航路点O1和O2为飞越航路点，飞机在内或外排序边飞至末端还未收到直飞融合点指令时，飞机可自主飞至飞越航路点后飞向融合点；由于飞机从外排序边飞向融合点时要经过内排序边，防止发生冲突，一般内排序边的高度高于外排序边。

2.2 点融合进近4D航迹预测模型

设飞机Fij是排序边j飞行的第i架飞机，有n架飞机通过内排序边进入点融合进近模式，有m架飞机通过外排序边进入点融合进近模式，j的取值范围是j=1，2，j=1为内排序边，j=2为外排序边，i的取值范围是i=1，2，…，n，m。其飞行位置可用四维坐标(d，φ，h，T)表示，其中d为飞机当前位置距融合点的水平距离(m)，φ为飞机当前位置和融合点的连线逆时针旋转到点融合进近模式对称轴所经过的角度(度)，h为飞机当前的飞行高度(m)，T为开始计算的时刻到飞机所处的位置为(d，φ，h)时所经过的飞行时间(s)。

阶段1：排序边飞行阶段。进入点融合进近模式至收到直飞融合点指令前，飞机的四维坐标计算如下方法

图1 点融合进近模式系统结构

(1)

式中：dj为内或外排序边距融合点的水平距离(m)；t为飞机当前的飞行时刻；te，Fij为飞机Fij进入点融合进近模式的时刻；VTAS，Fij(VCAS，Fij)为飞机Fij在当前飞行高度的真空速，由指示空速VTAS，Fij计算得到(m/s)；lj为内或外排序边的长度(m)；hj为内或外排序边的高度(m)。

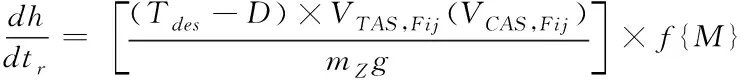
(2)

式中：D为飞机所受的阻力(N)；mz为飞机在航段r的重量(kg)；g=9.80665m/s2；Tdes为飞机在航段r下降时的推力(N)；f{M}为飞机分配给爬升的能量分担系数。

hs为飞机当前位置距融合点的垂直距离(m)，飞机从点融合进近模式排序边下降到融合点所用的飞行时间tdes的计算方法如图2。

图2 计算下降段飞行时间流程图

点融合进近模式中飞机Fij获得管制员下发的可以下降指令时刻td，Fij计算如下方法

(3)

式中：tt，Fij为飞机Fij收到直飞融合点指令的时刻。

阶段2：直飞融合点阶段。收到直飞融合点指令至收到可以下降指令前，飞机的四维坐标计算如下方法

(4)

阶段3：下降飞行阶段。收到可以下降指令至飞离点融合进近模式前，飞机的四维坐标计算如下方法

(5)

2.3 排序优化模型

2.3.1 决策变量

若飞机Fij在t时刻得到管制员下发的直飞融合点指令，决策变量Xt，Fij取值为1；若飞机Fij在t时刻未得到管制员下发的直飞融合点指令，决策变量Xt，Fij取值为0。

2.3.2 目标函数

为提高终端区的飞行效率和降低管制员的工作负荷，考虑先到先服务原则，应保证多机在点融合进近模式排序边的总飞行时间farc最低的前提下减小管制员调整各架飞机飞向融合点先后顺序的次数fc。目标函数计算如下方法

(6)

式中：TFij为飞机Fij在排序边上可行飞行时刻的集合(s)；C为管制员下发调整各架飞机直飞融合点指令先后顺序的次数。

2.3.3 约束条件

飞机Fij在点融合进近模式排序边上飞行时须获得管制员下发的直飞融合点的指令，如式(7)所示

(7)

飞机获得管制员下发的直飞融合点指令时前后两架飞机应满足规定的尾流间隔，设飞机Fab和飞机Fcd均为点融合进近模式内排序边上飞行或均为外排序边上飞行的前后两架飞机，则飞机Fab和飞机Fcd之间应满足如式(8)所示的尾流间隔

(8)

式中：tkl为多架飞机之间应当确保的最小尾流间隔(s)，其中k代表前机的机型，l代表后机的机型。

设飞机Fab为前机并且于点融合进近模式内排序边上飞行，飞机Fcd为后机并且于点融合进近模式外排序边上飞行，则飞机Fab和飞机Fcd之间应满足如式(9)所示的尾流间隔

(9)

式中：d0为内排序边与外排序边的纵向间隔(m)。

设飞机Fab为后机并且于点融合进近模式的内排序边上飞行，飞机Fcd为前机并且于点融合进近模式外排序边上飞行，则飞机Fab和飞机Fcd之间应满足如式(10)所示的尾流间隔

(10)

多机之间应确保其尾流间隔tkl满足尾流间隔规定的要求。为提高终端区运行效率，中南地区空管局与2019年12月5 日开始了航空器尾流重新分类(RECAT-CN)实验运行工作，采用的RECAT-CN最小尾流间隔标准见表1。

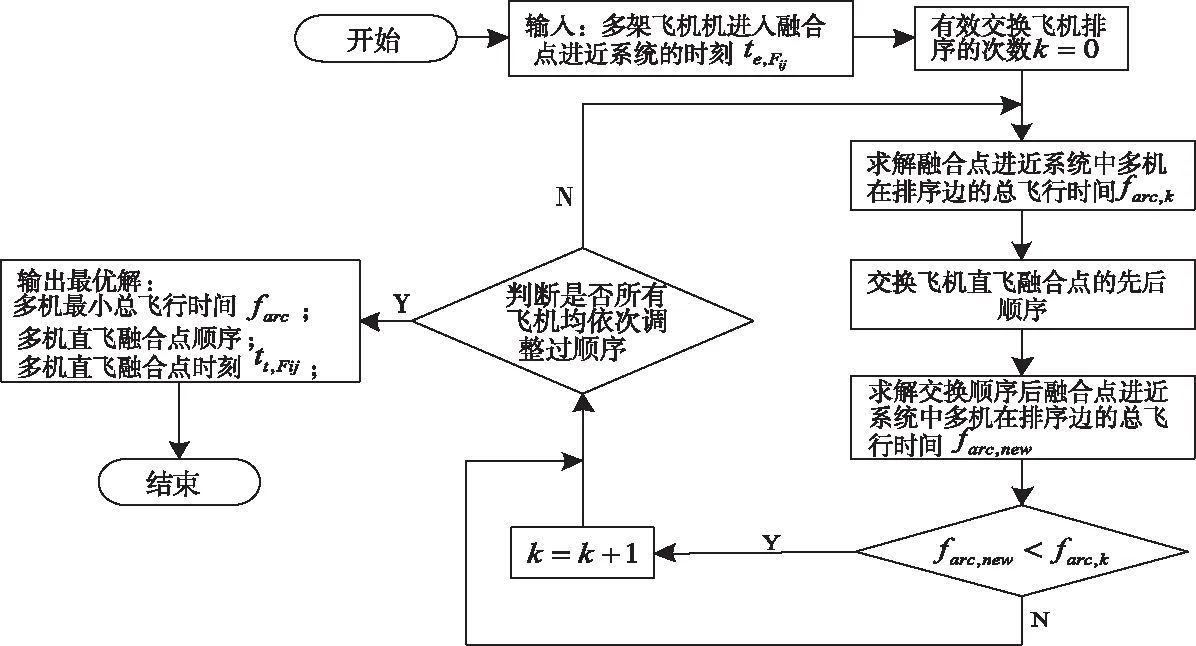
图3 优化系统总模型流程图

表1 RECAT-CN雷达间隔的尾流间隔标准(km)

2.4 优化模型的实现方法

利用分层迭代的思想在MATLAB中编程搜索求解，由于过大尺度的调整多机进近的先后顺序，不仅严重违背了先到先服务原则，且对在其之前到达飞机的飞行时间产生了延误累加。所以应在优化多机飞行效率的前提下减小调整各架飞机直飞融合点先后顺序的次数，其步骤可总结如下：

1)记录飞机进入点融合进近模式的时刻，按先到先服务准则，利用RECAT-CN雷达间隔的尾流间隔标准编程计算各架飞机直飞融合点的时刻，并将其设定为初始解。

2)将点融合进近模式外排序边上飞机转向融合点的时刻加上按其飞行速度飞到内排序边上所需时间，把两条排序边优化排序问题转化成一条排序边优化排序问题。

3)从较早进入点融合进近模式的飞机开始，按照顺序交换飞机直飞融合点的先后顺序，比较未交换顺序前多机在排序边上的总飞行时间与交换顺序后多机在排序边的总飞行时间，保留在点融合进近模式排序边上多机总飞行时间较小的多机直飞融合点的顺序。

4)固定第三步中求得的点融合进近模式多机在排序边上总飞行时间最小的直飞融合点顺序，转回第三步。

5)直到所有飞机都调整过直飞融合点的顺序比较过较小的总飞行时间后，保留多机在排序边总运行时间最小的可行解。

6)在搜索计算得到点融合进近模式多机在排序边总运行时间最小的可行解后，筛选出管制员下发调整各架飞机直飞融合点指令先后顺序的次数最小的可行解，求得最优解。

具体的优化系统总模型流程图如图3。

3 典型机场的点融合进近排序分析

3.1 仿真计算条件

构建的点融合进近模式系统结构的具体数据如下：内排序边与外排序边的纵向间隔d0=2nm；内排序边到融合点的水平距离d1=27nm；外排序边到融合点的水平距离d2=29nm；内排序边的长度l1=28.26nm；外排序边的长度l2=30.4nm；内排序边的高度h1=12000ft；外排序边的高度h2=10000ft；融合点的高度hmerge=6000ft；点融合进近模式的汇聚角θ=60°。

假定有20架飞机Fij排序等待进场，其中10架飞机Fi2从点融合进近模式的外排序边进入点融合进近系统，有10架飞机Fi1从点融合进近模式的内排边进入点融合进近系统，飞机Fij进入点融合进近模式的指示空速VCAS，Fij=250kt，不同机型之间应当保持的最小尾流间隔tkl满足RECAT-CN尾流间隔标准，飞机从外排序边飞到内排序边所需时间t0=25s，飞机Fi1在点融合进近模式内排序边可行飞行时刻的集合TFr1∈(1，353s)，飞机Fi2在点融合进近模式外排序边可行飞行时刻的集合TFr2∈(1，362s)，多架飞机Fij的进场数据见表2。

表2 多架飞机进场数据

3.2 优化模型的有效性验证

根据多架飞机进入点融合进近模式的时刻te，Fij，结合先到先服务原则和RECAT-CN雷达间隔的尾流间隔标准，利用MATLAB编程求解出点融合进近模式各架飞机直飞融合点的时刻tt，Fij作为初始解，求解得到的多架飞机初始解数据见表3。

序号机型tt,Fijtarc,Fij/s序号机型tt,Fijtarc,Fij/s5B76307:16:5011715A32007:24:301846B73807:17:3411316B74407:24:461707B76307:17:5010617B76307:26:011828A32007:18:5915218B76307:26:171359B73807:19:1514119B73807:27:2615310B74407:19:5612720B73807:27:4293farc2574 s

根据建立的考虑间隔约束的点融合进近多机排序模型，利用分层迭代的思想在MATLAB中编程求解得到使得点融合进近模式多机在排序边总飞行时间最小的多机排序和各架飞机直飞融合点的时刻如下表所示，由表4可知，通过考虑间隔约束的点融合进近多机排序模型的优化求解，点融合进近模式多机在排序边的总飞行时间减小到了1908s，优化调整后各架飞机的进近顺序为1、3、2、4、5、7、6、8、9、11、10、13、12、14、15、17、16、18、19、20。通过调整2和3、6和7、10和11、12和13、16和17航班直飞点融合的顺序相较于优化前的飞行时间减少了25.9%，明显有效的提高了点融合进近模式多机协同进场的飞行效率。

表4 最优多机进场排序与直飞融合点时刻

3.3 多机4D航迹预测方法有效性验证

20架飞机Fij在终端区点融合进近模式中进入终端区点融合进近模式的时刻te，Fij、直飞点融合的时刻tt，Fij、开始下降的时刻td，Fij和飞离终端区点融合进近模式的时刻tf，Fij飞机所处的飞行位置见表5。

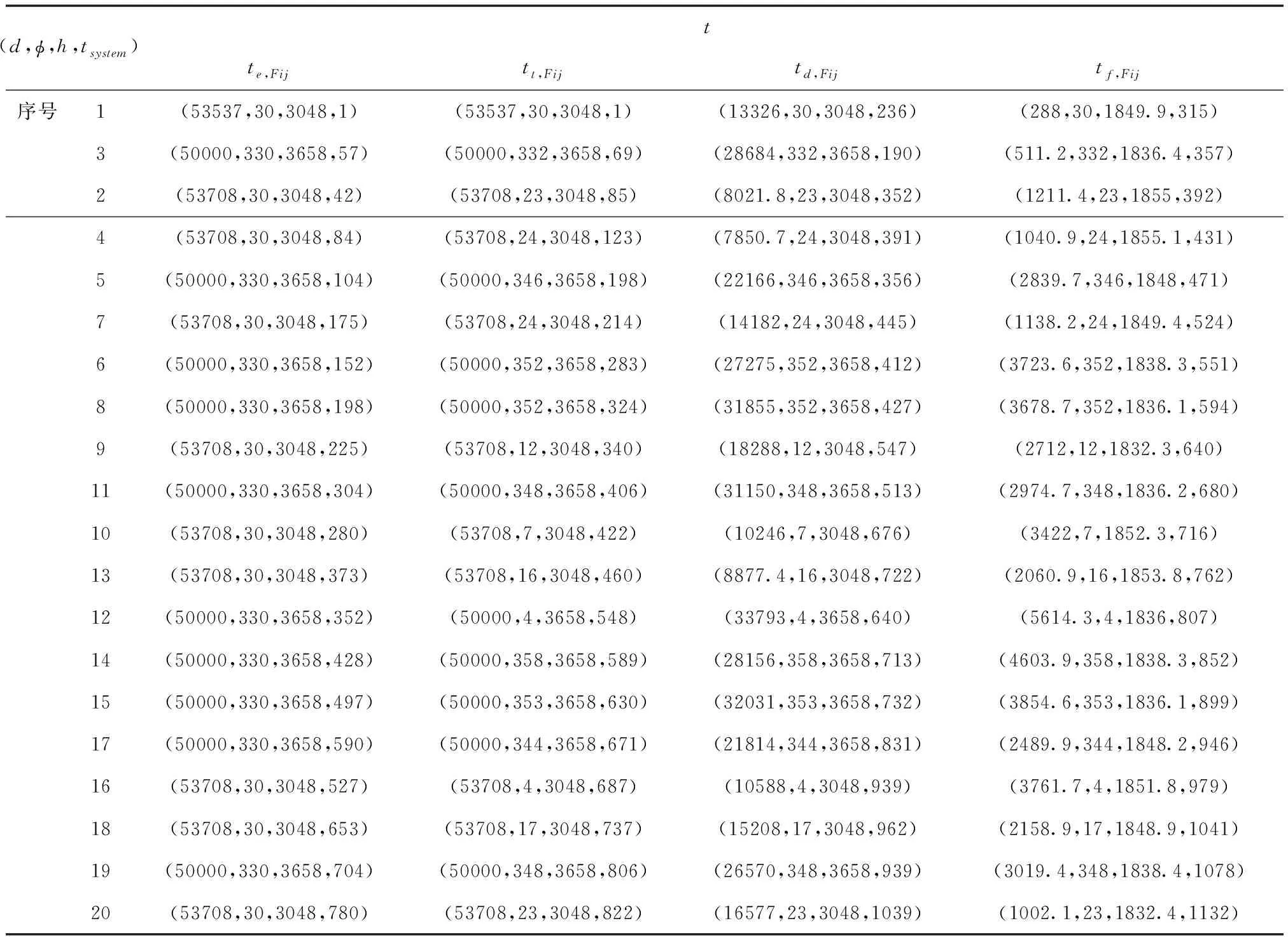
表5 终端区点融合进近模式飞机飞行位置

终端区点融合进近模式20架飞机Fij的4D航迹如图4。

图4 20架飞机的4D航迹

4 结论

本文构建了终端区点融合进近模式多机排序优化模型并对其优化求解，并且介绍了终端区点融合进近模式飞机4D航迹的预测方法，通过算例仿真验证，提出的方法能满足运行的实际需要。所得结论如下：

1)通过分层迭代的思想在MATLAB中编程对构建的终端区点融合进近多机排序模型优化求解，可降低终端区点融合进近模式多机的总飞行时间，进而降低多机运行成本。

2)考虑飞机性能来预测终端区点融合进近模式飞机4D航迹，能在实际运行中更加准确有效的定位飞机在终端区点融合进近模式的实时位置，更进一步确保运行安全。