RB工况下“机跟炉”协调控制系统分析与仿真
解剑波,胡伯勇,何郁晟,王印松
(1. 浙江省能源集团有限公司,浙江 杭州 311121;2. 浙江省火力发电高效节能与污染物控制技术研究重点实验室,浙江 杭州310000;3. 浙江浙能技术研究院有限公司,浙江 杭州310000;4. 华北电力大学自动化系,河北 保定 071000)
1 引言
随着我国清洁能源电力事业的迅速发展,可再生电力能源得到了不断的利用[1]。为了确保电力系统能够对清洁的电力能源做到正常消纳,火电机组需要在40%额定负荷甚至更低负荷进行调峰任务,维持电力系统安全运行。
相比于高负荷段,低负荷段火电机组对象的特性有很大差别,机组主要运行参数的稳定性更低,辅机运行的状况对机组的影响也更大。伴随着火电机组在运行时存在诸多的不确定因素,机组自动处理问题的能力不足,现场运行人员的应急操作不及时,导致重要辅机在机组投入AGC的情况下易发生跳闸突发事件。
除制粉系统外,在低负荷下一旦单侧的辅机发生故障,另一侧的辅机仍然能够保证机组的正常出力。当参与深度调峰的机组在低负荷下辅机跳闸,一般不会触发RB控制,而是会将负荷响应速率更快的“炉跟机”协调运行方式切换为“机跟炉”的运行方式,以维持各运行参数的稳定。
目前,有关RB工况下“机跟炉”协调控制系统的机理分析与仿真研究还比较少。在RB工况下,如果机组在运行期间处理问题不合理,对该工况下系统对象的特性理解不深刻,将为机组运行甚至电力系统的负荷分配工作带来不便。为了火电机组能够安全运行,维持电力系统调度的正常工作,本文进行了RB工况下“机跟炉”负荷控制系统的分析与仿真工作。结合有关文献内容,建立了350 MW超临界单元机组对象模型,该模型根据机组低负荷滑压运行的工作特点,利用蒸汽量方程实现了炉侧与机侧的分离,为系统的机理分析带来了便利。同时,根据对象特性建立了 “机跟炉”仿真协调控制系统,通过仿真结果,对参与深度调峰的机组给出了系统调节措施建议。
2 系统模型的建立
有关协调控制系统对象的研究有很多成果,其中文献[2]以文献[3]给出的单元机组锅炉侧汽压被控对象机理模型为基础,提出了一种单元机组增量式机理模型,对系统机理做到了详细的描述且得到了验证。文献[4]通过理论推导得到的“机跟炉”机侧等效对象,能够反应系统机侧输入输出的特性,便于对单元机组对象进行炉、机侧的分离。
本文考虑,机组在低负荷发生辅机跳闸事故后,以“机跟炉”的协调方式在RB工况下继续进行发电任务,此时炉侧是对机组负荷和主蒸汽压力造成主要影响的一侧(滑压运行)。要对“机跟炉”协调控制系统的炉侧做到详细的分析与研究,需要做到炉侧和机侧的有效分离。保证炉侧对机组重要参数造成影响的机理模型不变,将机侧的扰动特性进行简化。由此,本文以典型的汽包炉为例,得到了单元机组控制对象,如图1所示。

图1 单元机组控制对象
图中相关参数说明:M-燃料量;KM-燃料量M变化引起炉膛热负荷Qr变化的比例系数;τM-M变化到Qr变化的滞后时间;DQ-用蒸汽流量单位表示的锅炉汽水容积吸热量,是代表热负荷Qr的信号,又称为热量信号;Cb-蓄热系数,代表锅炉的蓄热能力(即锅炉蒸汽压力每改变1MPa时锅炉所释放出的蒸汽量);Pb-汽包压力;Rgr-过热器的动态阻力;D-锅炉蒸汽量;DT-汽机通汽量;CM-蒸汽管路的容量系数;PT-主蒸汽压力;PTμ-汽机扰动后的主蒸汽压力;RTr-汽机动态流通阻力系数;KT-汽机调节阀静态放大系数;DTM-汽机通汽分量,接通2路时有效;μT-汽轮机进汽调节阀阀门开度;W1(s) -为变对象;W2(s) -为等效一阶“负”对象;W3(s) -为等效二阶对象。
图1中,1通路是以锅炉蒸汽量作为扰动变量的通路,2通路是以汽轮机进汽阀门开度作为扰动变量的通路。当接通1路时W1(s)为整体汽轮机通汽量至机组功率间的传递函数,当接通2路时该对象为炉侧汽轮机通汽分量至机组功率间的传递函数。W2(s)在接通2路时有效,与文献[4]中G12(s)环节相似(汽轮机调节阀门开度至主蒸汽压力的扰动特性,“负”指主蒸汽压力随阀门开度呈反向变化,可等效通汽量至蒸汽压力的环节)。W3(s)在接通2路时有效。与文献[4]中G22(s)环节相似(汽轮机调节阀阀门开度至机组功率的扰动特性,可等效通汽量至机组功率的环节)。
“机跟炉”运行方式下的协调控制系统,当汽轮机调门开度不发生变化的情况下(滑压运行),系统各重要参数会取决于炉侧。由于汽机流通蒸汽量DT是主蒸汽压力PT、汽机背压及汽机调节阀开度μT的函数,是系统炉侧和机侧重要的结合点。因此本控制对象主要依据汽机流通蒸汽量DT进行系统炉侧和机侧的拆分。通常汽机背压变化很小,可假定汽机调节阀为线性,该环节的动态特性一般近似为

(1)
定义来源于炉侧的汽机通汽分量DTM,该环节的动态特性为

(2)
如图1所示,在滑压运行下,汽轮机进汽调节阀门开度不变,将汽机流通蒸汽量进行分离后,控制对象能够对炉侧和机侧进行拆分。接通1路时,系统模型即类似于文献[2]中给出的机理模型,该模型炉侧与机侧为整体,可根据机理对整体系统的特性进行分析。接通2路时,由于机侧利用了阀门扰动等效替代蒸汽量扰动,炉侧机理模型不变,便于单独对系统的炉侧进行机理分析。
在RB工况下,该单元机组控制对象又主要呈现出以下几个特点:
1)一般而言,主蒸汽母管容积容量系数Cm远小于汽包炉汽水系统蓄热系数Cb[5]。
2)辅机减少,锅炉蓄热系数会发生变化。燃烧不稳定,炉膛温度低。要避免燃料量出现过大波动,防止炉膛灭火。
3)避免汽机进汽阀门开度出现过大波动,防止汽轮机振动、胀差、轴向位移增加。
4)负荷较低,避免进汽阀门开度激减,防止蒸汽压损,应适当进行滑压。
5)在低负荷段,机组各参数的稳定性下降,对外界扰动更加敏感。
6)AGC未投退,负荷需要跟随调度指令。
根据以上特点,本文依据“机跟炉”协调控制的一般方式(炉侧调节功率,机侧调节蒸汽压力),针对图1的控制对象建立了“机跟炉”负荷控制系统,如图2所示。

图2 “机跟炉”控制系统
控制系统在低负荷段发生跳闸时,除制粉系统外,不存在辅机出力不足的问题,其控制的重心应放在保证各项主要参数的稳定上。图2建立的控制系统,炉侧根据功率偏差进行PID运算,通过燃料量进行负荷调节。机侧汽轮机阀门开度不变,适当滑压,避免阀门开度出现大波动,防止蒸汽冲转前由于节流带来的能源损耗。由于该系统炉侧对象为增量式对象,其内部主要反映了系统重要参数的波动特性。若给予主蒸汽压力初值需要等待系统达到稳态,因此在仿真过程中蒸汽压力主要以观察波动范围为主。
3 控制系统稳定性分析
对于图1中的控制对象,主要有以下几个环节构成:
1)燃料量对锅炉的影响

(3)
燃烧和传热过程是一个复杂的化学过程,燃料量改变,首先将释放的热量传给受热面的锅炉金属管壁,再传给锅炉的汽水容积。式(3)为较为实用的一个关系式。
2)锅炉受热面
若利用蒸汽流量单位代表锅炉汽水容积吸热量,则流入热量与流出热量的动态热平衡方程如下

(4)
对于锅炉受热面,流入热量是燃烧后传给受热面的热量,并有一部分储存在锅炉中;输出量为蒸汽中的热量。根据动态平衡方程可得
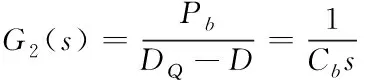
(5)
3)汽机动态流通阻力

(6)
该方程仅考虑了过热器的流通特性,汽包压力Pb为进口压力,主蒸汽压力PT为出口压力。锅炉蒸汽量与过热器流通阻力及进、出口压力差有关,其动态关系可近似为比例特性。
4)蒸汽管路的容量

(7)
蒸汽管道及汽机调节阀门组成的环节,其流入量是锅炉的蒸汽量D,流出量是进入汽机的蒸汽量DT。主汽压力PT可反映流入、流出蒸汽量的物质平衡关系。
5)汽轮机动态流通阻力
该环节关系式已给出,见式(1)、式(2)。
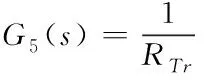
(8)
6)汽轮机做功环节:
①当接通1路时,根据文献[2]、文献[3]给出的机理模型可知,W1(s)为二阶对象,假设
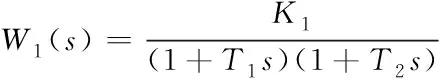
(9)
②当接通2路时,燃料量对蒸汽压力和机组负荷的扰动特性极为相似,故W1(s)可近似为一比例环节,假设
W1(s)=K2
(10)
由于控制系统保持汽机调门开度不变,机组滑压运行,负荷和主蒸汽压力完全取决于炉侧扰动,此时系统可视作SIMO控制系统。综上,根据图1可利用Mason公式[7],得到燃料量M至机组负荷Ne的闭环传递函数
前向通道:
P=G1(s)G2(s)G3(s)G4(s)G5(s)W1(s)
三个回路
l1=-G2(s)G3(s)
l2=-G3(s)G4(s)
l3=-G4(s)G5(s)
其中,l1与l3不相交。
则特征式
Δ=1+G2(s)G3(s)+G3(s)G4(s)+G4(s)G5(s)+
G2(s)G3(s)G4(s)G5(s)
若按照1通路的模型进行系统分析,则系统的传递函数为
其中
M(s)=T1T2CbRgrCMRTrs4+
(T1T2(CMRTr+CbRgr)+(T1+T2)CbRgrCMRTr)s3+
(T1+T2)(CMRTr+CbRgr)s2+T1T2s2+CbRgrCMRTrs2+
(CMRTr+CbRgr)s+(T1+T2)s+1
若按照2通路的模型进行系统分析,则系统的传递函数为

(11)
经过相关运算,通过结果可知,在分析系统时,若采用1通路进行系统分析,得到的系统传递函数较为复杂,炉侧和机侧作为整体,为“机跟炉”协调控制系统进行机理分析带来了较大困难。将系统机侧利用等效环节替代后,炉侧和机侧能够合理的分离,燃料量至机组功率的关系可得到极大的简化。
结合工程实际,燃料量对机组负荷的扰动特性应当是自稳的。但是当系统是以1通路为机理模型的系统,得到的传递函数较为复杂,若使用相关系统理论进行分析时,如Routh[7]判据,则要利用复杂的Routh阵列,且当机组发生跳闸后,系统多个参数均会发生变化,机理分析十分困难。以2通路为模型的系统,由于系统各项参数均大于零,利用Routh判据可知系统始终稳定,结论与实际相吻合。
4 仿真研究
利用MatLab/Simulink进行系统仿真,机组参数参考了文献[6]中给出的相应参数。
4.1 两个通路的模型比对
试验目的:分别搭建1、2通路模型,采用相同的控制器参数,观察曲线结果是否接近以验证等效模型的有效性。
本仿真过程:超临界350 MW机组,机组投入AGC,功率跟随调度指令。起始指令130 MW,50 s时目标负荷135 MW,400 s时目标负荷130 MW。仿真结果如图3所示。
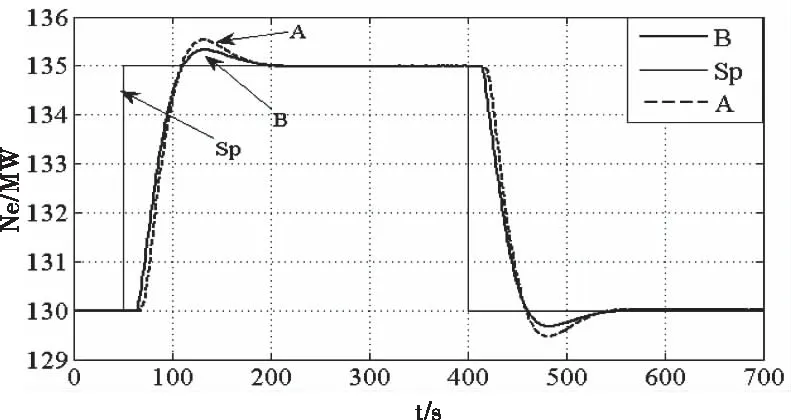
图3 两个通路模型的功率仿真结果对比图
图3中,A曲线为1通路模型,B曲线为2通路模型,Sp为拟调度功率指令。根据图3仿真结果,可以计算系统相应的品质指标,结果列为表1。

表1 系统调节品质指标
由表1的结果可知,通路1和通路2的功率调节品质指标数值接近,在汽轮机调节阀门开度不变时(即机组滑压运行),通路2和原通路1的系统调节特性极为相似。由于2通路中,功率扰动将汽机侧的通汽分量简化,造成功率的超调更小。1、2通路的系统峰值相差的数值很小(0.03 MW),各项调节品质指标接近,均在可接受范围内。同时,2通路系统对象传递函数更为简便,需要进行分析的系统参数更少,该模型可有效替代通路1模型。
通过系统分析和仿真的结果,均验证了本文给出的机组等效机理模型的有效性。
4.2 RB工况仿真
试验目的:炉主控制器参数不变,根据辅机跳闸情况改变系统参数。观察系统调节品质变化,以提供RB工况下系统调节措施。
对于协调控制系统,可以针对不同的辅机跳闸情况给予相应的处理方法,一般的跳闸情况有三种:制粉系统跳闸、送引风机跳闸以及一次风机跳闸。
制粉系统跳闸,当某台制粉系统停运后,燃料量迅速降低,但由于给煤机的出力会迅速上升,使得总煤量得到回升。当某侧引风机跳闸时,同侧送风机会联锁跳闸。因为单侧辅机能够带载机组半额定负荷左右的能力,当单侧风机跳闸后,另一侧侧送、引风机出力能够迅速上升。当单台一次风机跳闸后,相应的磨煤机会联锁跳闸,另一台一次风机液耦开度会迅速提升。这三类辅机跳闸在低负荷下,机组依然能够保持协调控制方式运行。
三种跳闸情况,会对机组的燃料量、炉膛压力、汽包水位、一次风压以及总风量造成影响,这些参数使得工况发生了变化,会使机组炉侧对象参数相应改变。由此进行系统仿真,改变机组炉侧的相应参数,控制器参数不发生变化,观察控制过程是否会发生变化甚至出现失调情况。
仿真过程:超临界350 MW机组,机组投入AGC,功率跟随调度指令。处于低负荷130 MW,给煤量58 t/h,主蒸汽压力为9.1 Mpa,滑压运行,汽包压力10.1 Mpa。调度起始指令130 MW,200 s时目标负荷135 MW,1500 s时目标负荷127 MW,1800 s时目标负荷137 MW。
仿真结果见图4、图5,仿真过程中机组相应的参数见表2。

图4 机组功率仿真结果图

图5 机组主蒸汽压力仿真波动图
观察图4和图5的仿真结果,可知在机组滑压运行下,汽机调节阀门开度不变,机组功率和主蒸汽压力的变化趋势相似,且三组曲线功率均能够跟随指令数值,主蒸汽压力波动在可接受范围内。机组在“机跟炉”运行方式下,负荷调节速率较慢。
由结果可知,当机组发生辅机跳闸情况时,如若未采取跳闸应对措施,系统各参数的变化会对调节过程产生影响。若控制器参数不发生变化,辅机跳闸后,随着各机组各参数的改变,系统始终接受外部调度指令,机组调节品质下降严重。

表2 单元机组仿真参数
5 RB工况下系统调节措施建议
在实际工程中,机组低负荷段运行时,由于辅机跳闸不会对机组的出力产生限制,因此一般不触发RB控制,而是在这种RB工况下继续进行发电任务,机组协调控制的运行方式切换为“机跟炉”方式,并在投入AGC的情况下继续接受调度指令。根据仿真结果,可知辅机跳闸后低负荷段各参数的稳定性较差,继续接收外部指令进行变负荷将对参数造成更大的扰动,不利于机组的运行安全。因此,在低负荷段,如发生辅机跳闸时,也应仿照高负荷段的RB控制策略,将锅炉主控切为手动控制,并保持当前的出力;同时,汽机进入跟随模式,稳定主汽压力。采用该运行方式,锅炉侧输出基本保持不变,有利于锅炉参数的调整和稳定,可避免辅机跳闸时外部指令和信号对机组出力产生扰动,保障机组运行安全。
除制粉系统跳闸外,为应对单侧辅机跳闸后造成的出力不足情况,控制回路中设计了相应的超驰回路。使得机组在单侧辅机跳闸后,控制逻辑会自动将跳闸前辅机指令叠加至运行侧辅机,以达到快速增加运行辅机出力的目标。在高负荷阶段,由于单侧辅机出力不足,发生辅机跳闸后采用该方法一般都将运行侧辅机的出力提升至最大,以满足RB过程中的参数控制要求。但对于低负荷工况来说,单侧辅机运行时其出力依然有裕量,且单侧辅机运行的工作点、效率都发生了变化,采用简单的指令翻倍方法很可能造成出力过大,反而影响机组的运行安全。
在本次仿真中,使用相同的控制器参数,系统在低负荷段的调节性能对于机组参数的改变表现十分敏感。由于实际火电机组中,各调节系统的主要参数设置均主要考虑高负荷段的工况,对于低负荷段的自动调节品质,特别是在单侧辅机运行时的调节参数方法调整并不多。低负荷段,各调节对象的特性和辅机工作点的变化,其控制参数与高负荷段有较大差别。因此,建议对相关PID控制器采用变参数设计,在参数赋值时考虑辅机运行工况、机组运行负荷等因素,根据不同的组合确定控制参数,以达到最佳的控制性能。
6 结论
本文针对工程实际中机组低负荷的RB工况,给出了一种RB工况下的“机跟炉”协调控制系统模型。根据机组滑压运行的特点,通过蒸汽通汽量方程对系统进行炉侧和机侧的分离,从而实现了系统的简化。并通过理论计算以及系统仿真,验证了模型的有效性。同时,通过进行机组跳闸仿真,为RB工况下系统调节提出了改进措施建议,为工程实际中机组面临的辅机跳闸问题提供建议性的解决方案。
限于篇幅,本文仅针对三种炉侧机组参数进行了仿真对比。在工程实际中若利用本模型进行控制系统的分析,需要得到较为精确的机理模型参数,这类参数辨识方法可参考有关文献。本文意在对低负荷RB工况的协调控制系统进行介绍和分析,从而对控制对象以及控制系统做到深入理解,对电厂安全运行、电力系统电力分配工作有重要的意义。

