基于混合数值算法的锯齿形喷管气动噪声仿真

闫国华，冯叔阳

(中国民航大学航空工程学院，天津 300300)

1 引言

随着大涵道比涡扇发动机的广泛应用，作为现代涡扇发动机主要噪声源之一的喷流噪声已经降低到与风扇噪声相当的量级[1]。但随着国际民航组织(International Civil Aviation Organization，ICAO) 开始采用更加严厉的第五阶段噪声标准[2]，我国国产大飞机也将面临更严峻的适航审定。因此在建立自己的拥有噪声预测评估能力的民用航空器噪声审定技术研究体系方面，在整机噪声中依旧占主导地位的喷流宽频噪声依旧是研究重点，

对喷流噪声的产生机理、噪声预测以及降噪手段等方面的探索有很多的理论和实验研究。TAM、VISWANATHAN等人[3][4]揭示了亚音速喷流噪声的产生主要是由于湍流的掺混导致的。Kawai S[5]等分析了亚音速到超音速下自由剪切层的不稳定性对喷管整体基础流场的影响。Samimy[6]等人对Tab齿形的降噪原理进行分析，揭示了锯齿产生的对旋涡对喷管流场剪切层内的掺混的增加作用。NASA开展多项实验[7][9]，在消声室对一系列不同锯齿结构小型喷嘴(Small Metal Chevron Nozzles)在不同测试条件下进行噪声测量，这一系列试验既取得了喷管流场的时均值和湍流脉动量的信息，也得到了喷管远场检测点的噪声总声压级和频谱信息，其实验数据常被用来检验喷流噪声预测方法的可靠性和精度。

通常使用两种计算方法来计算预测喷流噪声，一种基于半经验公式的预测模型，如SAE算法[10]、Pao算法[11]和Stone算法[12]等。二是基于声类比的数值计算方法，如基于FW-H方程的Ligthill声类比方法[13]以及考虑流体可压缩性的Mohring声类比[14]。尽管半经验模型在快速评估噪声级方面具有先天的优势，但是其无法精确的解析噪声频谱结构，不能对噪声的产生机理进行分析，且有严格的使用范围。如今，伴随着计算机技术的发展，数值计算已经渐渐成为了计算喷流噪声的主流方法。

采用计算流体力学(Computational Fluid Dynamics，CFD) 和计算航空声学( Computational Aeronautical Acoustics，CAA) 混合方法对喷管进行噪声数值计算[15]。首先对喷管的喷流流场进行瞬态数值计算，在瞬态流场的计算结果的基础上提取喷流噪声体声源，对其进行声传播计算，得到近场和远场的声学求解，并采用 NASA 的实验数据[7]对流场以及噪声计算结果进行对比验证。

2 喷管几何模型

研究对象是NASA实验用的SMC002号4锯齿小型金属喷管[7]，根据 NASA 提供的喷管数据完成建模，其三维模型如图1所示。喷管为单流通通道的收缩喷管，尺寸如图2所示，喷管进口直径65.85mm，出口直径53.6mm，出口安装4个Chevron型锯齿，齿长32mm，齿弯角5°。

图1 喷管模型

图2 喷管尺寸

3 喷流流场数值计算

3.1 流场计算方法

精确的流场解析是声学仿真的基础，为了保证流场计算量适中以及流场计算的精度要求。瞬态喷流流场的计算选择介于直接求解N-S方程和雷诺时均模拟之间大涡模拟(LES)，来提取喷流噪声声源。LES首先将N-S 方程进行滤波处理，其中对平均流动影响较大的大尺度量涡流通过N-S方程直接求解，而主要起耗散作用的小尺度涡流因其各项同性的特点，则通过亚格子模型求解，从而保证流场解析的精度。

(1)

其中由滤波操作而得到的大尺度量定义为

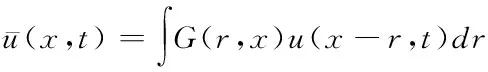
(2)

式中积分遍布整个流体域，G(r，x)是空间滤波函数，喷流流场的小尺度运动的尺寸和结构由其决定。

将过滤函数作用于N-S方程，得到紊流的控制方程

(3)

(4)

3.2 流体计算域及网格

为保证喷流流场充分发展，以半径为500 mm、长2070 mm的圆柱体作为喷流计算域，将SMC002喷管包裹。采用结构网格对计算域进行六面体网格划分，喷流流通区域进行O型拓扑。为了满足大涡模拟计算要求，设置壁面附面层第一层网格距离y+值为1，使得第一个网格位于湍流粘性底层区域。为了更好捕捉喷管出口剪切层内的涡流，在喷管出口区域进行局部加密，生成初始网格，总节点数184万，总网格数190万。计算域网格分布细节如图3所示。

图3 喷嘴周围的网格

为了确定喷流流场瞬态计算中网格数量与计算结果之间的无关性，再准备一种90万数量网格和150万数量网格，分别对三种不同密度网格进行试算，监测出口中心线马赫数并进行比较，结果如图4所示。稀疏网格计算结果与初始网格和加密网格结果有微小差别，而初始网格与加密网格计算结果几乎相同。因此，初始网格可以满足LES计算需求。

图4 网格无关性验证

3.3 边界条件及求解设置

为了加快喷流流场的收敛，首先使用RNGk-e模型进行稳态喷流流场计算，将此稳态流场作为LES瞬态求解的物理初场。选取NASA实验中的冷喷流实验来确定边界条件[7]，具体边界条件如下：

1) 进口边界条件：喷嘴入口采用压力入口，进口总压178200 Pa，总温288.15 K；

2) 出口边界条件：喷嘴出口采用压力出口，总压97700 Pa，总温280.2 K；

3) 远场边界条件：远场采用压力远场，总温总压与出口边界条件相同。

3.4 流场计算结果

图5为SMC002喷流速度时均分布云图，其中喷口流速达到297.773 m/s，接近 NASA[7]实验要求的出口流速0.9马赫的工况。由此可见，该实验为亚音速无限空间内淹没射流。整个喷流流场可大致划分为三段，混合区包括了保持与喷管出口速度相当的势流核心以及混合层，其中势流核心区长度0.25 m；过渡区域内即为时均速度衰减区，这一区域内喷流速度急速衰减到100 m/s左右，区域长度与混合区大致相同；之后即为流体自维持流动的充分发展区，流体保持低速流动。

图5 SMC002喷流流场结构

图6为SMC002喷流湍流动能的时均分布云图，可以明显看出势力核心区域湍流动能极小，可视为层流流动区域；而整个混合区域内围绕在势流核心周围的混合层为强湍流区域，中间区域湍流动能最大，并一直向后延神，并超过势流核心区延伸到过渡区内，强湍流区域围绕势流核心上下对称，沿轴线方向面积增大，在过渡区内开始衰减，在最后的充分发展区维持低水平状态。

图6 SMC002喷流湍流动能结构

图7是喷口出口截面时均速度云图，喷流高速区域在两锯齿之间向外部低速区域扩散，相比于锯齿顶尖由喷流最大速度到外界静止空气间巨大的速度梯度，高速喷流从两锯齿之间逐渐地向外渗出，两锯齿之间的流体速度梯度减小。Chevron型锯齿有效的增大了喷流面积，从而起到了更好的掺混作用。

图7 喷管出口速度云图

图7为喷管出口截面的湍流动能云图，锯齿顶尖湍流动能极小，而强湍流区域出现锯齿两边，沿锯齿顶尖的轴向对称，并在两个锯齿之间开始向外部衰减扩散，只要的湍流分布区域向两锯齿之间集中。

图8 喷管出口截面湍流动能云图

在定常计算基础上进行瞬态计算，图9喷管出口附近涡量云图，喷管出口之后，高速气流与外部低速气流形成了脱落涡，涡流主要分布在混合区的混合层内和过渡层和充分发展层内，及涡流集中强湍流区域以及湍流扩散区域内，势流核心区域内涡流分布不大，整体的涡流伴随气流向后高速流动；图10为喷管出口截面涡量云图，出口处，高速气流与外部低速气流之间形成了强烈的剪切环，涡流集中大声在两锯齿之间，向四周扩散。

图9 喷管出口附近的涡量云图

图10 喷管出口截面涡量云图

由此可见，高速射流喷入静止空间，强烈冲击静止空气，与其进行了急剧的掺混，高速的喷流气体与周围静止空气形成了环形的混合层，混合层内的涡流带来强烈湍流，涡流伴随高速流体向后流动衰减，湍流也在过渡发展区之后开始衰减；而锯齿的加入，增大了两锯齿间的掺混，也使得两锯齿间的涡流增大，湍流增大。

图11为瞬态0.025 LES计算的喷管出口之后中心线速度分布曲线。其中纵坐标u/Uj为喷流速度u与喷流最大速度Uj的比值，横坐标X/Dj为喷口出口中心向方向距离X与喷口出口直径Dj的比值。与NASA实验[7]SMC002号喷管结果进行对比，可以看出，LES方法的计算结果在靠近喷口出口的位置与实验值符合得更好，即核心区和实验结果吻合更好。

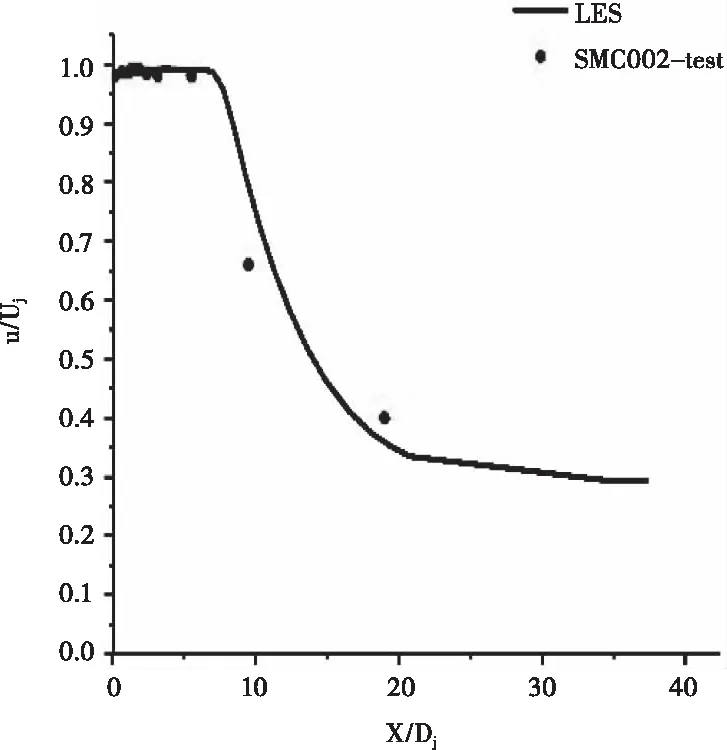
图11 SMC002喷管中心线速度分布

4 声场计算

4.1 CFD/CAA 混合求解流程

CFD计算得到产生声源的流场脉动量，以此为基础进行CAA声传播计算，完成声场求解。基于瞬态CFD和CAA联合求解气动噪声已经成为成熟且广泛使用的计算方法。图12为混合数值算法求解喷流噪声的基本流程图。

图12 声场求解流程图

SMC002号喷管声学求解过程如下：

1) 使用LES方法进行喷流瞬态流场计算，获得喷流流场密度、速度矢量；

2) 利用瞬态流场密度、速度矢量进行时域的喷流噪声体生源提取，在Actran中icfd模块完成；

3) 利用离散傅里叶变换( Discrete Fourier Transform，DFT)，将时域的声源信号变换到频域信号；

4) 将喷流噪声的声源点集映射到声学网格，基于Ligthill声类比理论进行喷流噪声声场求解。

4.2 Ligthill声类比方法

考虑到流动和声场的耦合以及方程的非线性给求解带来困难，因此将声学现象假设为线性问题，把声场分为近场声源区域和远场声传播区域，使流动与声场相分离。由此从N-S方程得到Ligthill方程

(5)

对(5)进行频域转[16]换得

(6)

式(6)中：ω为频率；Tij为Ligthill应力张量，可表示为：

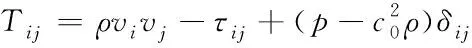
(7)

式(7)中：v为流体流速；c0为静止介质的声速；p为流体压力；xij为空间固定坐标。对(7)式进行有限元变分离散化即可得到以下声学解

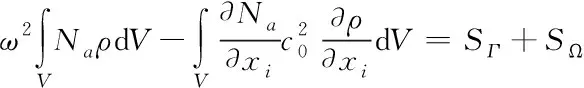
(8)

4.3 离散傅里叶变换

由于声传播的计算是以频域形式进行的，因此，必须将时域的喷流体声源进行离散傅里叶变换，公式如下

(9)

式(9)中，N为非定常流场采样的时间步数；Qn为频域信号，qk为时域信号。

4.4 声学网格和声学计算域

近场声压采用有限元计算喷流噪声声源以及近场声传播，远场场点采用无限元插值求解，从而精确求解整个喷流噪声声场。

4.4.1 网格尺度

4.4.2 声学计算域

在有限元计算区域，以流体计算域作为声源区；并向外增加10层网格区域，以此区域为声传播区域，将声传播区域边界面全部定义为无限元边界，噪声没有能量损耗以及反射，全透射传播出去。声学近场有限元计算域如图13所式。

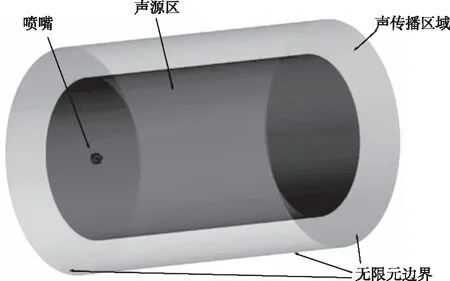
图13 声学计算域

声学远场区域部分，按照NASA实验要求建立远场场点[7]。喷流为轴向X轴，径向为YZ方向。在XY平面，以喷口出口中心为圆点，2.54 m为半径，在180°范围内每隔10°建立19个远场声压接收点，如图14所示。

图14 远场场点示意图

4.5 声场计算结果

近场噪声声压级如图15所示。与流场结果对比可以看出，声压级比较大地方集中在喷流混合区域内，特别是势流核心周围的强湍流区域的混合层内，相比于核心势流的声压，混合层的声压级要高其10dB以上。喷管出口的混合层内，大量涡量间的相互作用产生各种脉动量，因此强烈脉动湍流造成了喷流噪声的产生。整体喷流噪声沿着喷流方向发展，声压集中分布区域与湍流动能较大区域比较耦合，喷流噪声实质上反应了喷流湍流混合过程的涡旋变化。但是伴随频率升高，整体声压级逐渐降低，声压级的分布也更均匀。

图15 近场声压级

喷管出口近场声压级如图16所示，可以明显看出，声压级较高的地方集中在两锯齿之间周围，围绕齿缺处形成环状，并向外扩散。在1500.94 Hz下，锯齿之间周围声压级达到最大143 dB，而齿顶尖区域只有119 dB；2501.56 Hz下，锯齿之间周围声压级达到最大144d B，而齿顶尖区域只有121 dB；3302.6 Hz下，锯齿之间周围声压级达到最大130 dB，而齿顶尖区域只有110 dB；4552.85 Hz下，锯齿之间周围声压级达到最大124 dB，而齿顶尖区域只有109 dB；由此可见两锯齿相比于锯齿顶尖，锯齿周围声压级要高20 dB左右。随着频率升高，喷管出口整体声压级减小，而锯齿与齿顶尖的声压差距也有所减小。对比喷管出口的流场结果以看出，强声压区域同样于强湍流区域耦合；而锯齿的安装则大大增加了流场的掺混，使得流场的大尺度涡量破碎成小尺度涡量，从而使得齿顶尖噪声减小。

图17为远场场点噪声总声压级(OSPL)指向性图。噪声总声压级越靠近喷流流动方向越大，正对喷口方向的喷流噪声可达113 dB，从30°到120°范围内声压级变化平稳，在105 dB上下浮动。

图16 喷口出口近场声压级

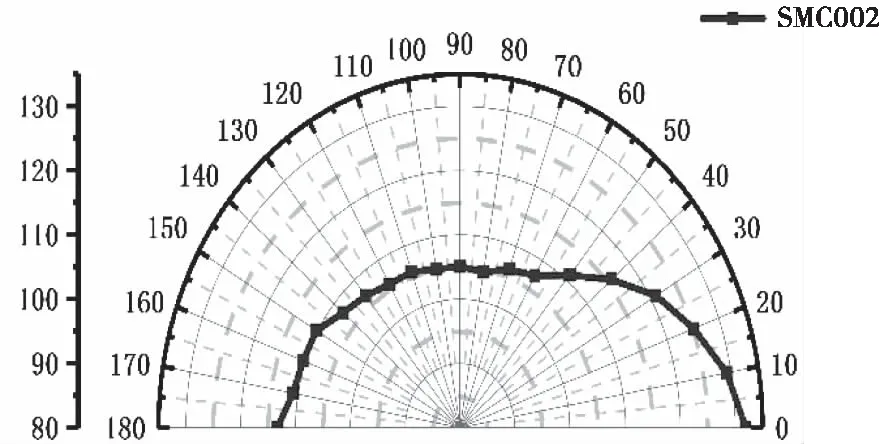
图17 噪声指向性特征图

取场点中0°、60°、90°、120°、150°为主要测量点，其频谱图如图18所示。其中，正对喷流方向的0°场点各个频率下的声压级都是最大。可以看出，整个喷流噪声声压级较大的部分都集中在2000 Hz以下的中低频段；2000Hz到8000 Hz段噪声变化平稳；而从8000Hz以上开始，声压级急剧衰减，高频段噪声因其在空气中容易被损耗有明显降低。

图18 主要测量点的噪声频谱曲线

为验证结果准确型，取4个主要场点与文献[7]的实验结果进行对比。使用实验中不同极坐标角度下的场点总声压级(OSPL)进行验证，数值计算结果与实验值的结果比较如表1所示。

表1 数据对比与计算误差

由表1可见，数值计算结构大多小于实验值，但是最大误差不超过3.5%，且大部分结果都偏小，出现此误差的原因可能是计算量的限制，使得在喷流流场的瞬态仿真计算上，网格不够密，从而无法捕获更破碎的涡，脉动涡量的计算误差从而使得声学仿真计算出现误差。但在航空器噪声适航噪声评估的工程计算上，这个计算精度可以接受。

5 结论

1)文章综合非定常喷流流场数值模拟方法、Ligthill声类比方法、有限元结合无限元方法实现并完成了对单通道的Chevron型锯齿喷管喷流噪声声辐射数值模拟，相比于适航上常用的半经验公式以及传统基于FW-H方程的声辐射数值模拟，能够得到近场噪声结果，以及详细声辐射特性，并且与流场信息得到更好的耦合，可以为发动机噪声结构设计提供参考。

2)喷流产生噪声的重要原因是高速气流冲击周围静止空气，形成的湍流带来了强烈脉动量形成噪声，喷流噪声主要在喷流流场中的混合层内产生，涡量大的地方湍流动能大，同时喷流噪声大。

3)Chevron型锯齿的安装使得喷管的喷流出口与外界静止空气的接触面积增大，掺混增大，两锯齿之间湍流动能相比于齿顶尖增大，脉动量也增大，在中地频段，齿顶尖声压级比锯齿之间声压级小20 dB左右。

4)喷流噪声主要是低频噪声，并且具有明显指向型，指向喷流流动方向，在远场噪声计算方面，喷流噪声数值计算结果与实验结果相比，误差小于3.5%，结果可靠。可用来进行飞机发动机喷流噪声预测，为喷管设计以及航空器噪声适航审定提供参考。