浮法锡槽入口段玻璃液流动过程模拟分析
陈淑勇,陈家睿,李 瑾,李从云,欧元勋,江 琦,左泽方
(1.浮法玻璃新技术国家重点实验室,蚌埠 233000;2.硅基材料安徽省实验室,蚌埠 233000;3.玻璃新材料创新中心(安徽)有限公司,蚌埠 233000;4.安徽凯盛基础材料科技有限公司,蚌埠 233000)
0 引 言
浮法玻璃工艺具有成本低、规模大等优点,可生产0.1~25 mm厚的平板玻璃,浮法玻璃在建筑、汽车、电子信息显示、光伏发电等领域具有广泛应用[1-2]。熔融玻璃液流入盛满锡液的锡槽,在锡液表面铺展、拉薄成一定厚度的玻璃带,玻璃液与锡液的接触、锡液氧化等原因将造成玻璃板锡斑、气泡、光学畸变点等缺陷,严重影响玻璃成形质量[3-5],因此,锡槽是浮法玻璃成形的关键设备。锡槽分为入口段、抛光区、拉薄区、冷却区,其中,锡槽入口段连接熔窑与锡槽,是影响浮法玻璃成形质量的关键。
在锡槽入口段,高温玻璃液由流道连续流入锡槽,并漂浮于锡液表面,在重力、表面张力、黏滞力作用下形成稳定的玻璃液层,继续流入抛光区、拉薄区、冷却区得到厚度均匀的玻璃带[6]。针对浮法玻璃锡槽入口段成形过程,国内外研究者进行了大量研究工作。Fernndez Oro等[7]建立了锡槽入口段气氛-玻璃液-锡液三相模型,基于流体体积法(volume of fluid, VOF)捕捉相界面,采用Fluent软件模拟分析了玻璃液流动与锡液循环流特征,并模拟得到了玻璃液平衡厚度。Xing等[8]采用Ansys Fluent 14.0软件建立了600 t/d锡槽入口段三维多相模型,采用流线分析了玻璃液成形过程与湿背砖区液流,并与玻璃断面条纹图进行了对比。Li等[2]采用Ansys Fluent 14.0软件模拟分析了唇砖高度对入口段玻璃液流的影响,结果表明增加唇砖高度有利于促进污染玻璃液流向玻璃带边缘,提高成形质量。Li等[9]采用Ansys Fluent 14.0软件建立了500 t/d锡槽入口段三维多相模型,分析了湿背砖宽度、八字砖夹角对玻璃液成形质量的影响,得到了优化的湿背砖与八字砖结构尺寸。锡槽正常投产后,难以对结构进行调整,而拉引量与玻璃液黏度易于调控,因此,深入研究流道玻璃液流量与黏度对锡槽入口段玻璃液流动的影响规律,对锡槽入口段的操作优化具有重要意义。
文献报道中对锡槽入口段的模拟研究均采用瞬态多相流方法,存在计算时间长、难以获得稳态结果的问题。因此,本文针对浮法玻璃锡槽入口段的玻璃液流动成形过程,提出了简化稳态多相模型,并采用Ansys Fluent 2019 R3软件对模型的可靠性进行了分析验证。进一步采用所建立的锡槽入口段模型,对不同拉引量、玻璃液黏度条件下玻璃液流动成形过程进行了模拟分析,得到了拉引量与黏度对玻璃液成形过程的影响规律。
1 锡槽入口段数值模型
本文研究的锡槽模型为锡槽流道入口至八字砖出口处。对于普通浮法玻璃,根据表1所示气氛、玻璃液、锡液的物性参数可知,锡液的黏度远远小于玻璃液(μG∶μT>105,其中μG、μT分别为玻璃液、锡液黏度),锡液对玻璃液流动的黏滞影响可忽略[10-12]。因此,本文对锡槽入口段模型引入如下简化假设:(1)忽略锡液对玻璃液流动的黏滞影响;(2)忽略玻璃液-锡液界面张力作用;(3)锡槽入口段温度恒定;(4)熔融玻璃液为不可压牛顿流体;(5)气氛为理想气体。

表1 物性参数
为降低模拟计算量,本文基于锡槽系统几何结构与流动状态的对称性[7],对锡槽宽度方向的半侧结构进行建模,如图1所示。
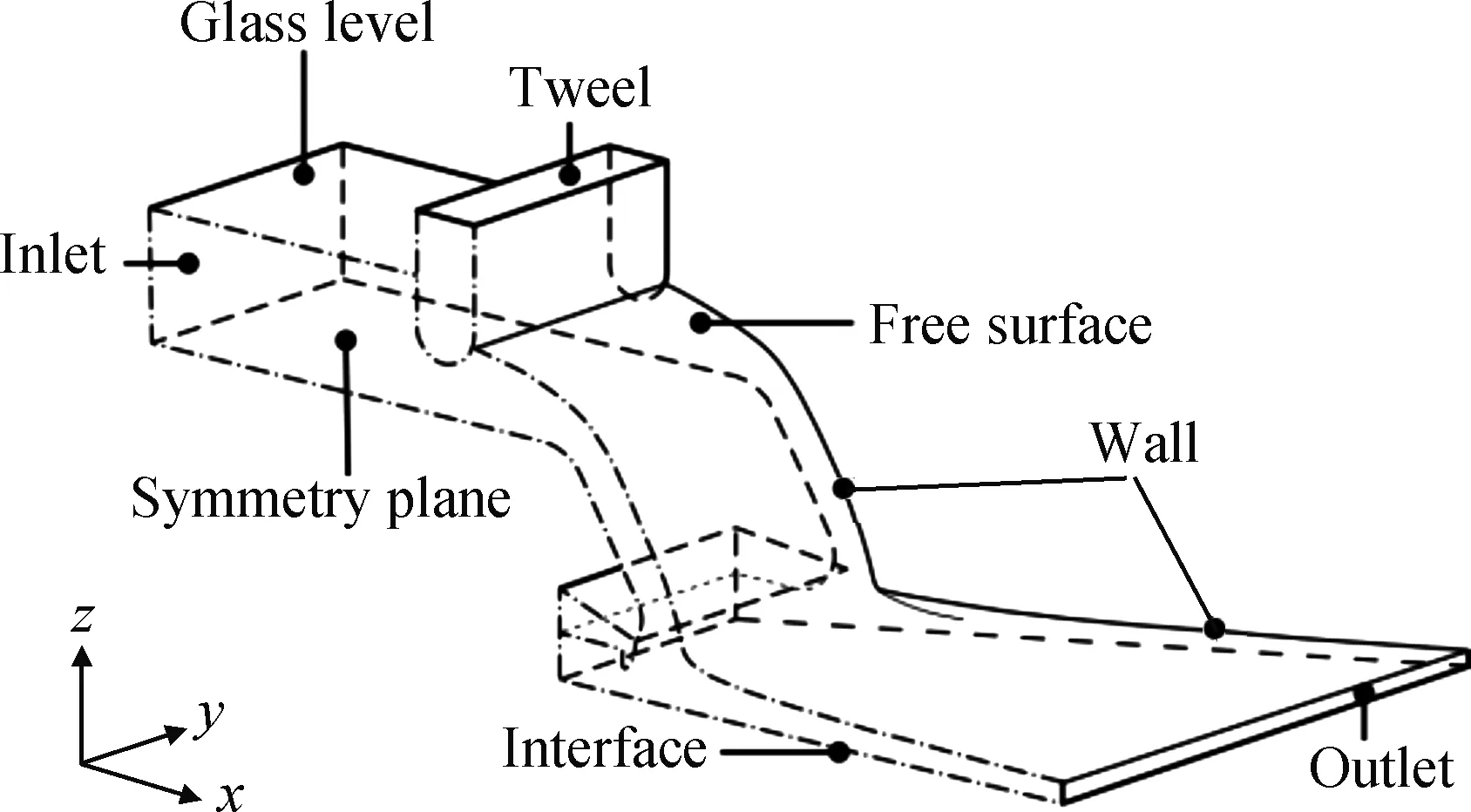
图1 锡槽入口段几何模型
1.1 稳态多相模型
浮法玻璃锡槽生产过程中,玻璃液的流动、温度分布等均处于稳定状态,可采用稳态多相模型进行描述。玻璃液在锡槽内为层流状态,基于前文引入的简化假设,图1所示简化锡槽模型中稳态多相流动过程的控制方程如下:
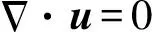
(1)
(2)

模型中气氛与玻璃液的相界面采用VOF处理。定义α为玻璃液相体积分数,控制方程如下[7]:
(3)
ρ=(1-α)ρA+αρG
(4)
μ=(1-α)μA+αμG
(5)
式中:α为玻璃液相体积分数;ρA、ρG分别为气氛、玻璃液密度,kg/m3;μA、μG分别为气氛、玻璃液黏度,Pa·s。
1.2 锡槽入口段数值模型
本文对某一拉引量为500 t/d的普通浮法玻璃锡槽进行模拟分析,锡槽入口段结构尺寸如图2所示。锡槽模型网格划分采用分块扫略方法,生成全六面体网格,并对重点区域网格进行加密,网格划分如图3所示。
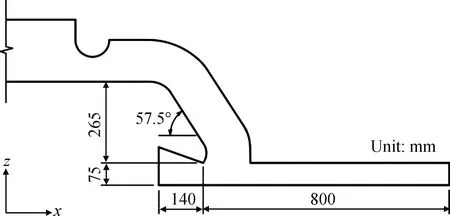
图2 锡槽入口段结构尺寸
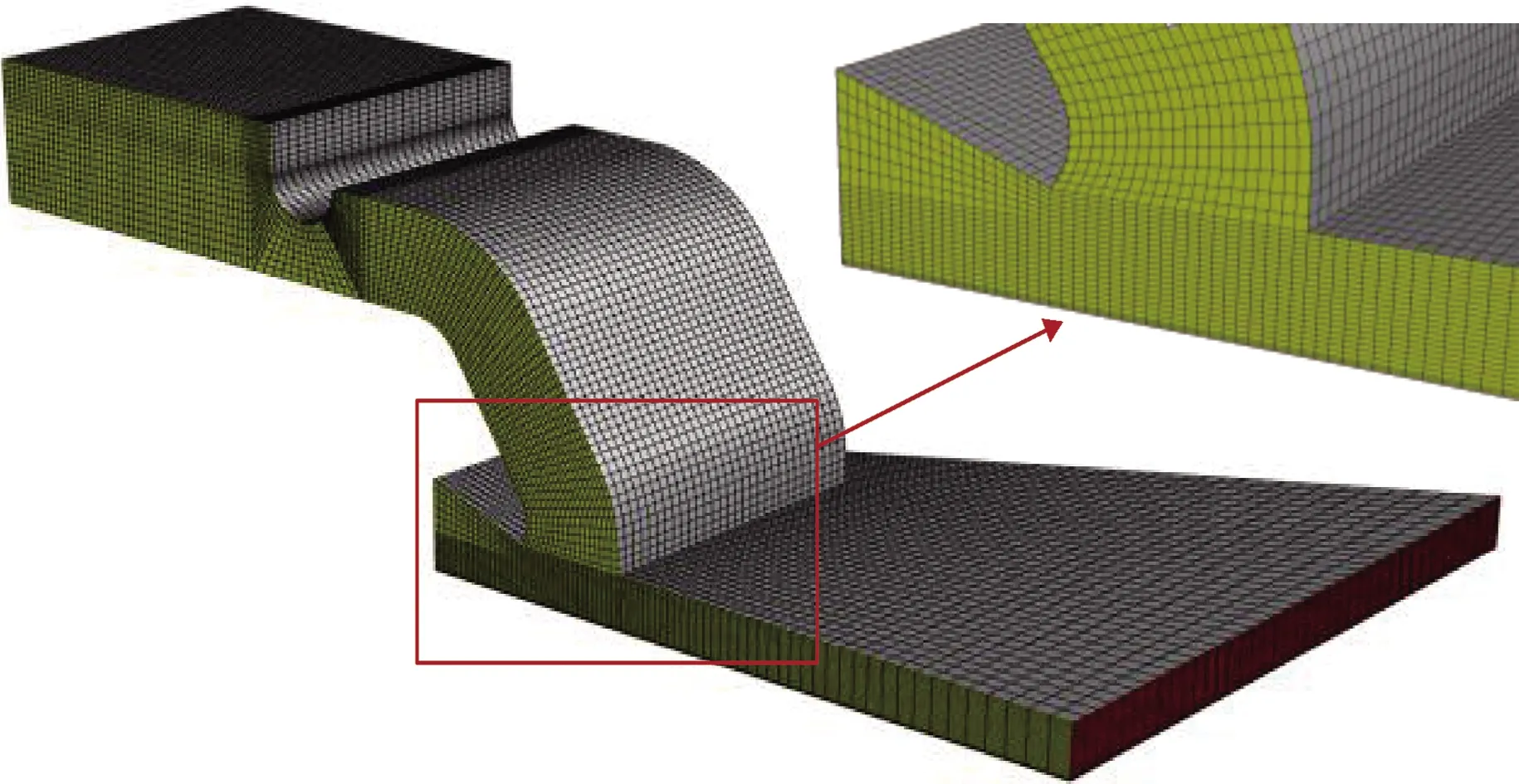
图3 锡槽入口段模型网格划分
选择的数值模型如下:速度项采用二阶迎风格式(second order upwind),压力项采用交错压力格(PREssure STaggering Option, PRESTO!),VOF采用基于压缩格式和交界面模型的变体格式(compressive scheme and interface-model-based variants),速度-压力耦合问题采用速度-压力同步更新求解的耦合算法(coupled scheme);采用伪瞬态(pseudo transient)欠松弛算法,以提高模型的计算稳定性;相间表面张力作用采用连续表面张力模型[2,7]处理,同时考虑相界面与壁面的接触角作用,对玻璃液的平衡厚度进行准确模拟。
图1所示锡槽模型中,模型边界条件如表2所示,表中uin为对应拉引量条件下玻璃液入口流速,n为边界处单位法线矢量,un为边界处法线方向上的速度大小。

表2 锡槽玻璃窑池模型边界条件
根据前文的简化假设,本文仅考虑锡液对玻璃液的浮力支撑作用,即图1所示Interface边界根据玻璃液层的厚度与压力发生变形。本文采用动态层(dynamic layering)动网格模型处理边界变形,并引入层状非对称加密方法对网格沿z方向进行加密,以保证模型网格的质量。
1.3 物性参数
本文所研究的锡槽生产的是普通浮法玻璃,所用保护气氛为H2体积含量为3%的N2和H2的混合气体,各材质的物性如表1所示。
2 玻璃液平衡厚度
玻璃液漂浮在锡液表面,在重力与表面张力作用下,将形成有限厚度的玻璃液层,其平衡厚度如下[10,14]:
(6)
γ=γG+γGT-γT
(7)
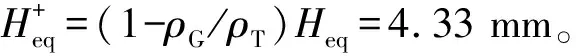
2.1 平衡厚度稳态多相模型
漂浮于锡液面以上的玻璃液部分,其界面轮廓符合杨-拉普拉斯(Young-Laplace)方程[15]:
Δp=γG(κ1+κ2)
(8)
Δp=ρgΔz
(9)
式中:Δp为界面两侧压差,Pa;κ1、κ2为界面主曲率,1/m;Δz为距离界面顶部的距离,m。
为验证本文所建立锡槽入口段稳态简化模型的准确性,对玻璃液漂浮于锡液表面的平衡状态进行了模拟,模型如图4所示,并采用前文所述稳态模型,对初始厚度为10 mm的玻璃液层铺展于锡液表面的平衡状态进行了模拟分析。
2.2 平衡厚度模拟结果
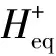
图4 玻璃液平衡厚度验证模型
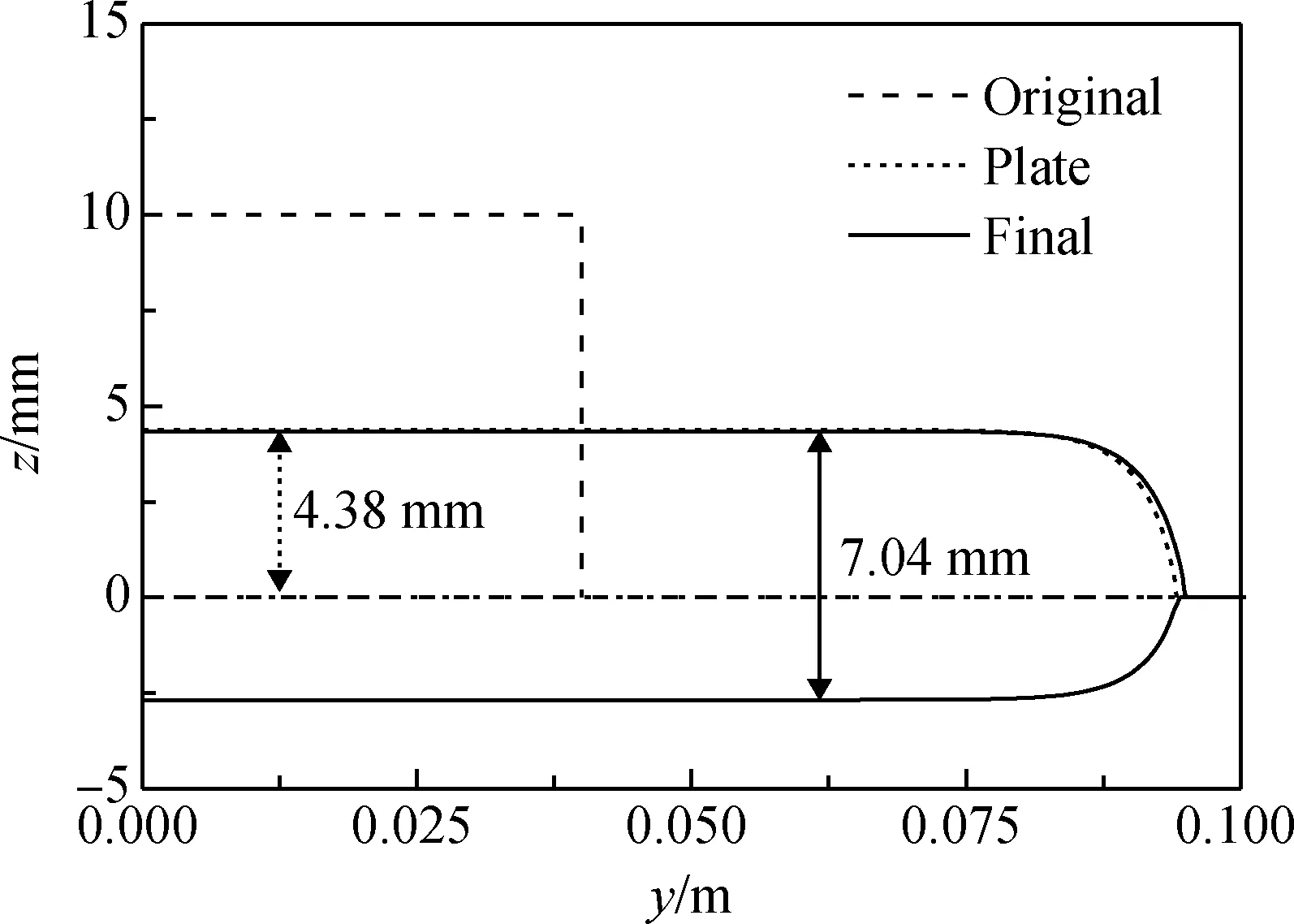
图5 玻璃液平衡厚度模拟结果
3 锡槽入口段玻璃液成形过程
采用前文提出的稳态多相模型,对图2所示的锡槽入口段玻璃液的成形过程进行模拟分析,锡槽工况为拉引量500 t/d,玻璃液黏度500 Pa·s。
锡槽入口段玻璃液-气氛界面的初始与收敛稳定后的轮廓如图6(a)所示,稳定后的流动铺展状态如图6(b)所示。玻璃液经由流道、唇砖流入锡槽八字砖区,并漂浮于锡液表面,在重力、表面张力作用下,逐渐摊平、铺展形成一定厚度的玻璃液层,在八字砖出口处形成一定厚度的玻璃带。
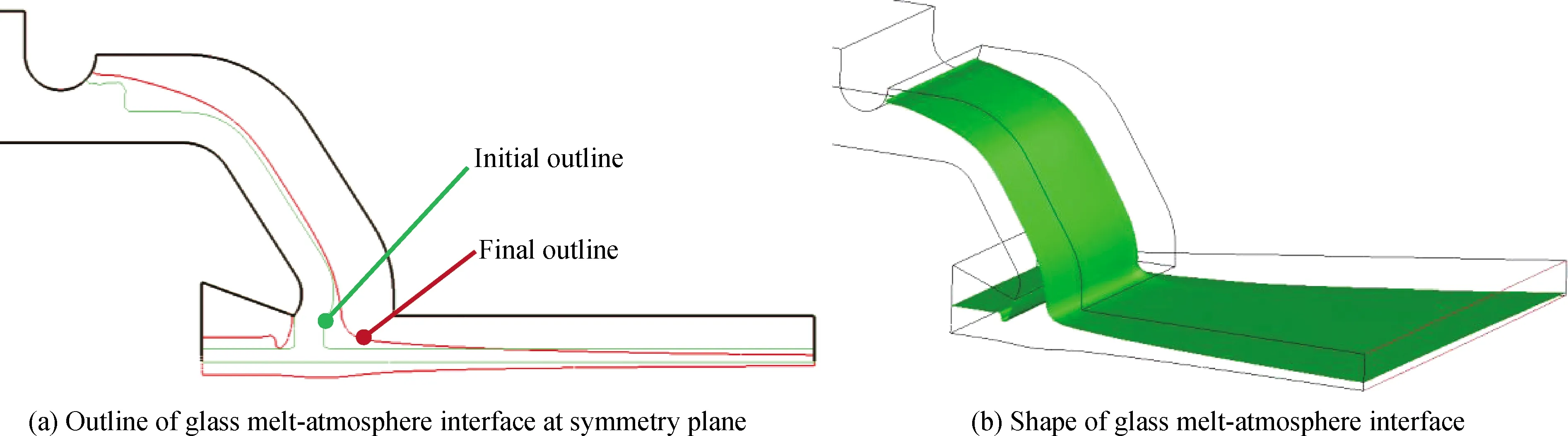
图6 玻璃液-气氛界面模拟结果
玻璃液速度矢量模拟结果如图7、图8所示,其中U为玻璃液速度大小。由中心对称面处速度分布(图7)可知:玻璃液在唇砖倾斜区域内,流速随着远离壁面而逐渐增大,在玻璃液-气氛界面处具有最大流速;唇砖后下方区域(湿背砖区),流速远低于其他区域,形成低流速的滞留玻璃液层;在八字砖区,玻璃液漂浮于锡液表面向出口区域流动,流速逐渐增大,而流速在厚度方向上无明显变化。锡槽入口段玻璃液流速整体较低,呈层流状态,且气氛、锡液的黏度远小于玻璃液,气氛、锡液对玻璃液的流速影响可忽略,因此,玻璃液流速主要受重力和锡槽壁面黏滞阻力的影响。
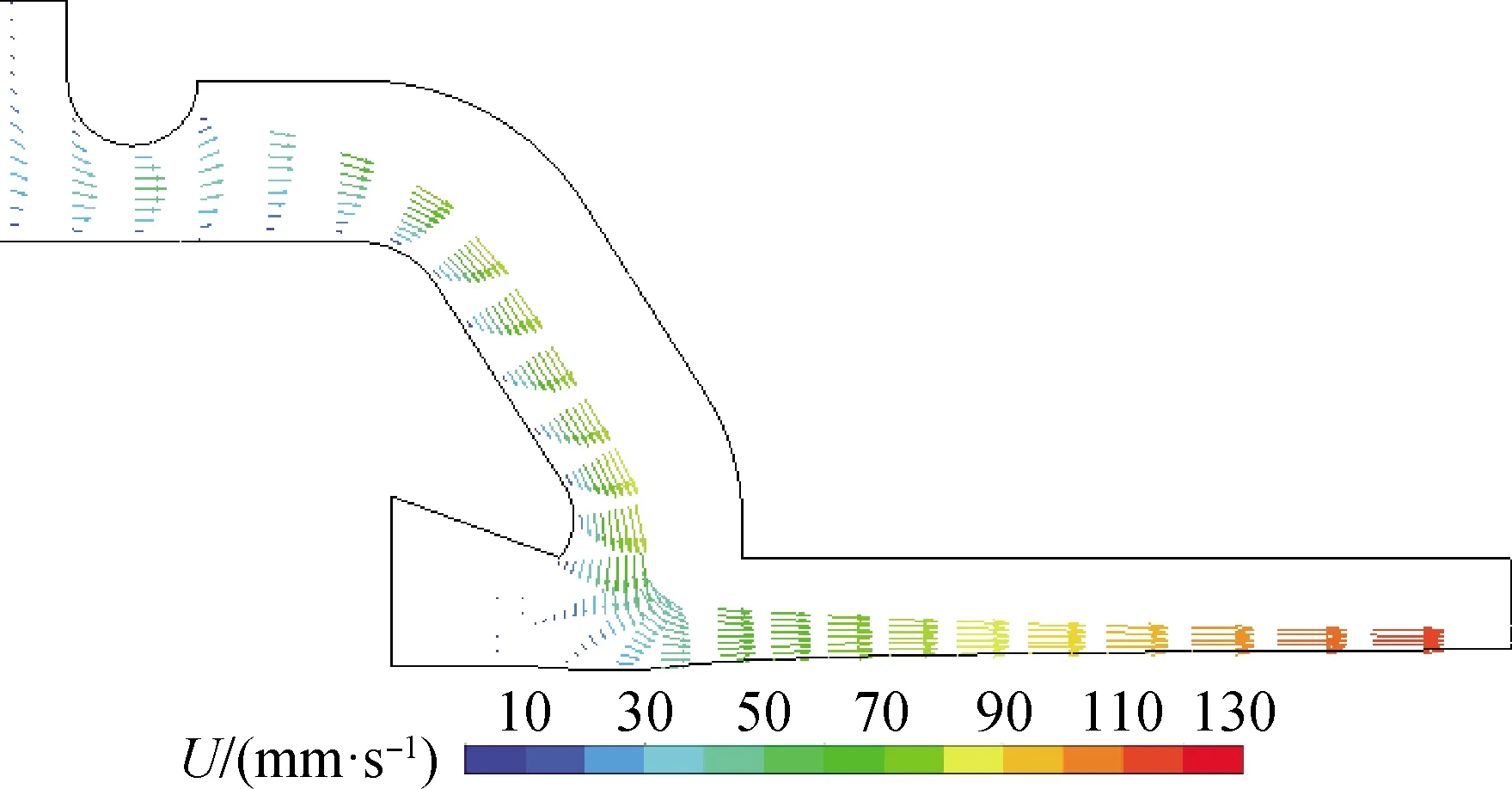
图7 对称面处玻璃液速度矢量模拟结果
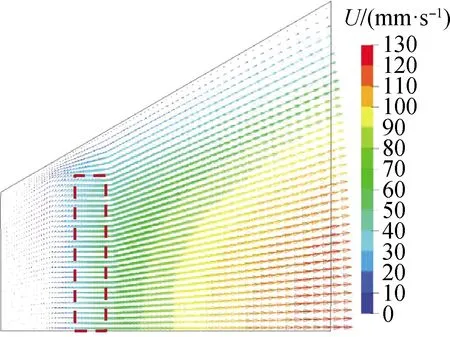
图8 玻璃液-锡液界面处玻璃液速度矢量模拟结果
由玻璃液-锡液界面处速度分布(图8)可知:玻璃液由唇砖流入锡槽时,流速在宽度方向上分布较为均匀(图8中虚线框区域);玻璃液在锡液表面向出口流动过程中,在重力、表面张力,以及八字砖限制作用下摊平铺展形成玻璃带,出口处流速分布呈中间大、边部小的特征。
根据模拟结果,分析了玻璃液在锡槽内的流线分布,如图9所示,其中颜色代表玻璃液沿流线由入口流至当前位置所用的时间(t)。由结果可知,由料道流入的玻璃液主要由出口处高流速区域(图8)流出,表明出口边部低速玻璃液主要来自湿背砖区域的滞留层,可有效降低滞留层玻璃液对玻璃液层成形质量的影响,与文献[16]中报道的分析结果相一致。
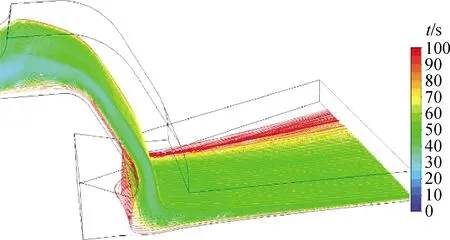
图9 玻璃液流线分布模拟结果
4 拉引量对玻璃液成形过程的影响
锡槽拉引量对玻璃液的流动状态与成形过程有显著影响,本节利用所建立的锡槽入口段模型,在玻璃液黏度为500 Pa·s条件下,模拟分析了不同拉引量条件下玻璃液的成形过程,重点分析了玻璃液流速分布与成形过程的变化。
4.1 玻璃液成形过程
根据模拟结果发现,当拉引量降低至300 t/d时,玻璃液层将无法充满模型出口,因此,本文选取拉引量350 t/d、400 t/d、450 t/d、500 t/d、550 t/d、600 t/d进行模拟分析。各拉引量条件下,对称面处玻璃液的轮廓模拟结果如图10所示。结果表明:各拉引量条件下,玻璃液在唇砖与锡液表面的流动成形样式保持一致;随着拉引量的增大,唇砖与锡液表面的玻璃液层均呈增厚趋势。
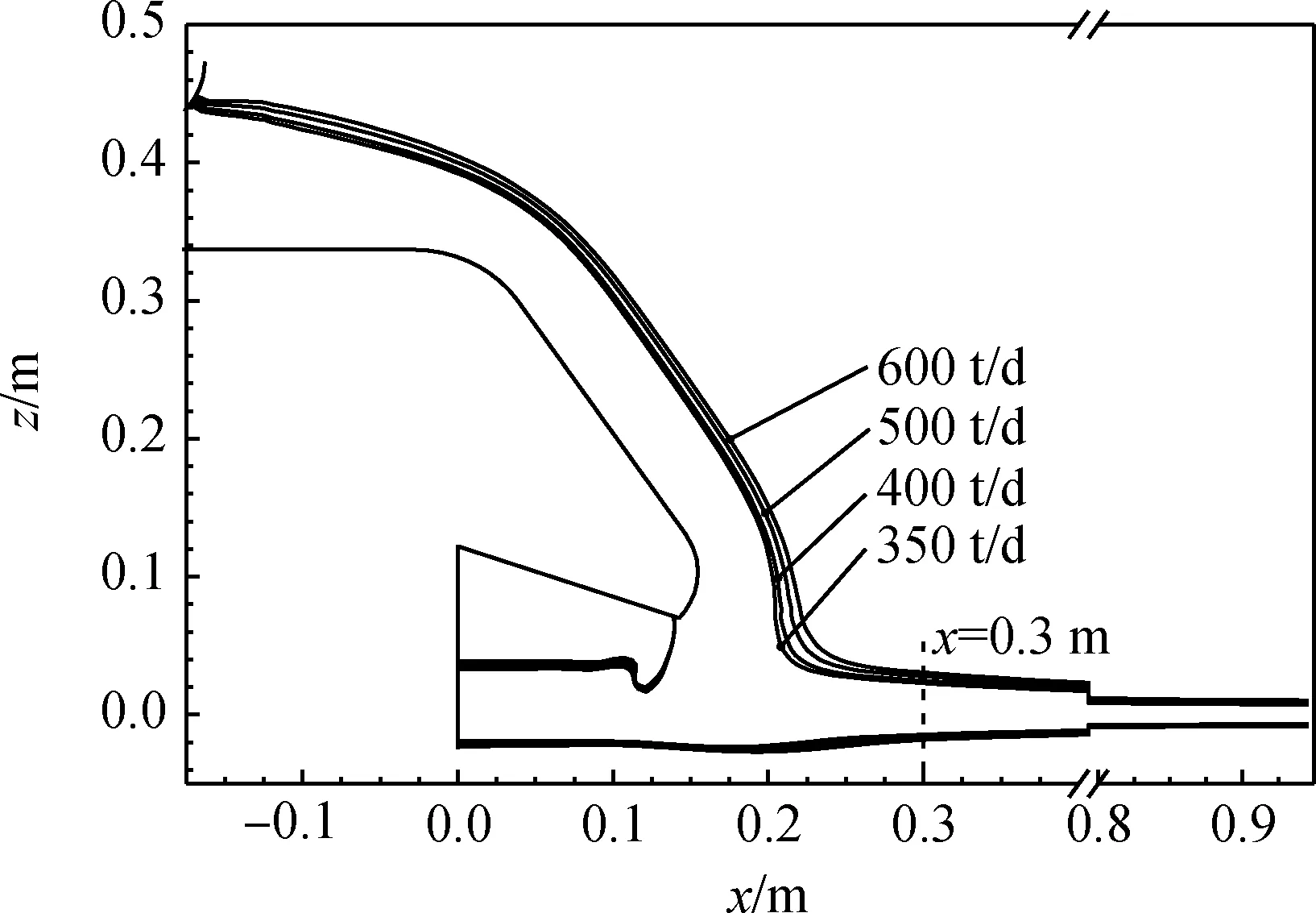
图10 不同拉引量条件下对称面处玻璃液轮廓
对于图1所示模型的唇砖区域,除靠近侧壁区域外,玻璃液流动状态为斜面上自由表面流,其液层厚度如下[17]:
(10)
式中:h为液层厚度,m;G为质量流量,kg/s;w为斜面宽度,m;β为唇砖倾角(见图2)。
根据图10所示结果,分别测量350 t/d与600 t/d条件下唇砖中部的液层厚度,其厚度比例为1∶1.202;按照式(10)计算得到液层厚度比例为1∶1.197,模拟结果与理论分析结果吻合良好。
玻璃液速度分布模拟结果如图11、图12所示。由x方向速度(Ux)分布可知,玻璃液流至八字砖区的锡液表面后,x方向速度与液层宽度逐渐增大,表明玻璃液处于不断摊平展薄的状态,逐渐形成一定厚度的玻璃液层;由y方向速度(Uy)分布可知,玻璃液横向摊平主要发生在距离对称面2/3宽度位置,这是由于唇砖宽度小于八字砖区宽度(如图1所示),且八字砖区域呈喇叭状,因此玻璃液的横向展平主要发生在八字砖区域的外侧,对玻璃带成形质量具有较大影响。此外,对比玻璃液x、y方向速度可知,y方向速度显著低于x方向速度,表明玻璃液在锡槽入口段主要表现为摊平展薄。
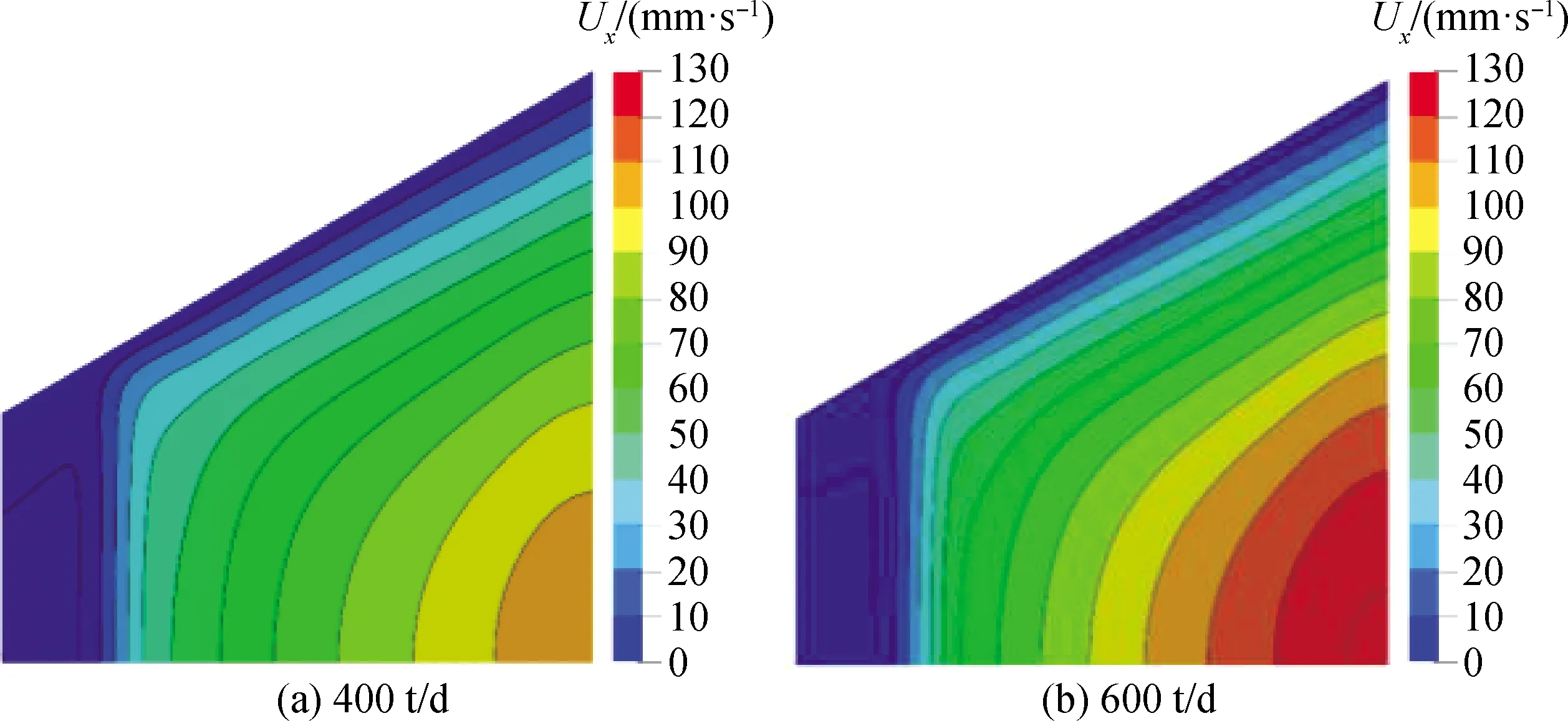
图11 不同拉引量条件下玻璃液x方向速度分布对比
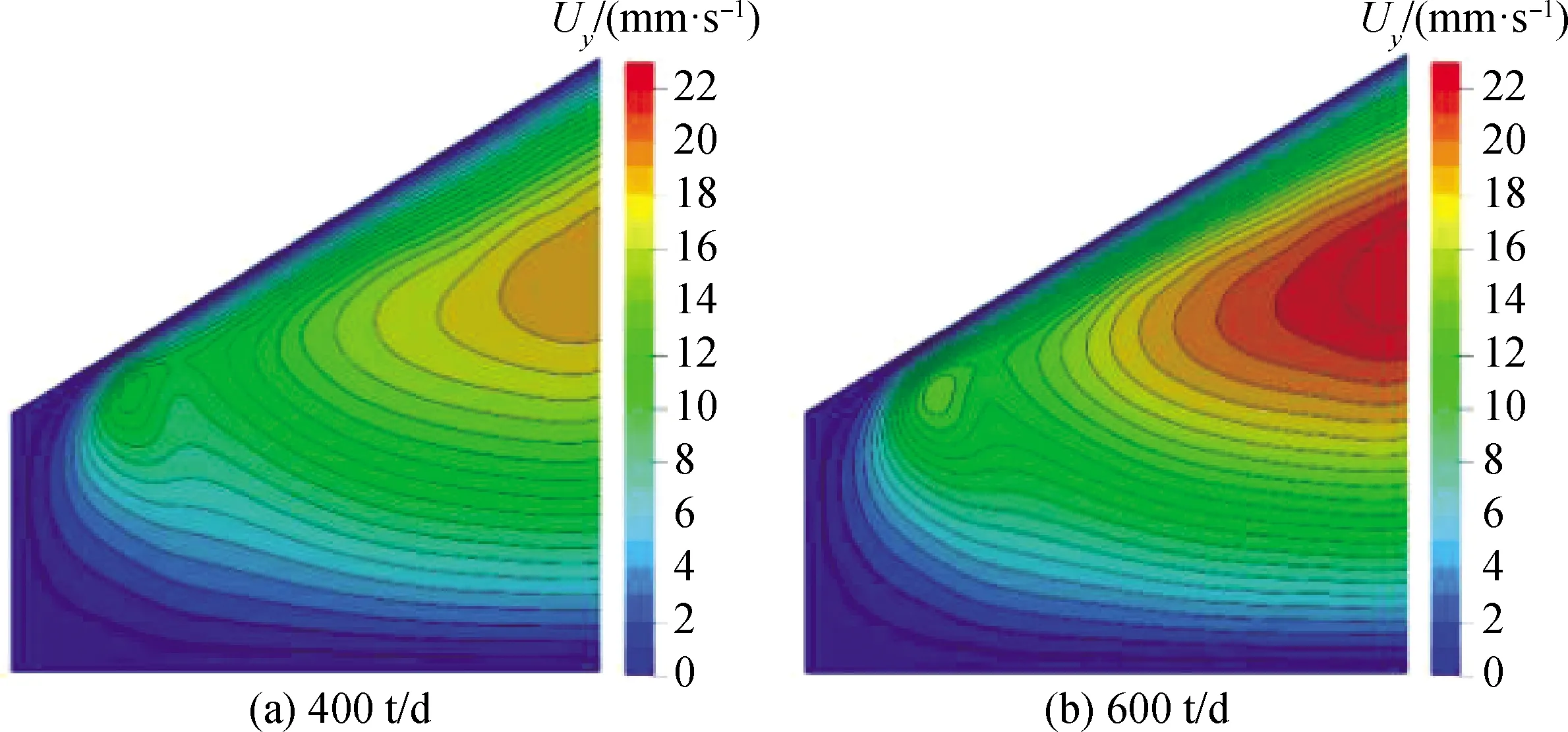
图12 不同拉引量条件下玻璃液y方向速度分布对比
不同拉引量条件下,玻璃液流速随拉引量的增大而增大,但各拉引量下玻璃液在x、y方向上的速度分布趋势保持一致。因此,在各拉引量状态下,漂浮于锡液表面的玻璃液横向摊平与纵向展薄过程较为稳定,锡槽生产负荷具有一定的调整空间。
4.2 玻璃液厚度分布
根据玻璃液-气氛、玻璃液-锡液界面位置模拟结果,计算得到八字砖区玻璃液的厚度分布,如图13所示。由结果可知,玻璃液在八字砖区域内,在x、y方向上逐渐铺展摊平,且厚度随拉引量增大而增加,这与前文分析结果一致。

图13 不同拉引量条件下玻璃液厚度分布对比
进一步对比了不同截面位置的玻璃液厚度分布情况。x=0.3 m截面处(截面位置见图10)玻璃液厚度分布如图14所示,可发现在唇砖宽度范围内,玻璃液厚度分布较为均匀,而在唇砖外侧出现明显的液位差。这是由于唇砖宽度小于下方锡液,玻璃液需由中部区域在重力作用下流入唇砖外侧区域。出口截面处玻璃液厚度分布如图15所示,可发现玻璃液层在重力驱动的横向铺展作用下逐渐摊平,但仍存在一定的厚度差。
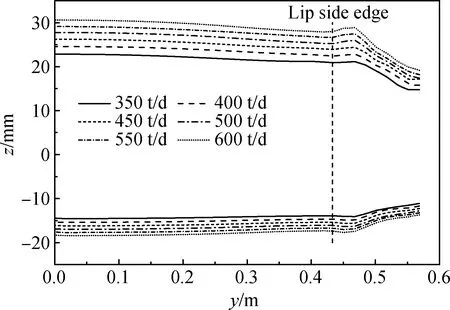
图14 不同拉引量条件下x=0.3 m截面处玻璃液轮廓
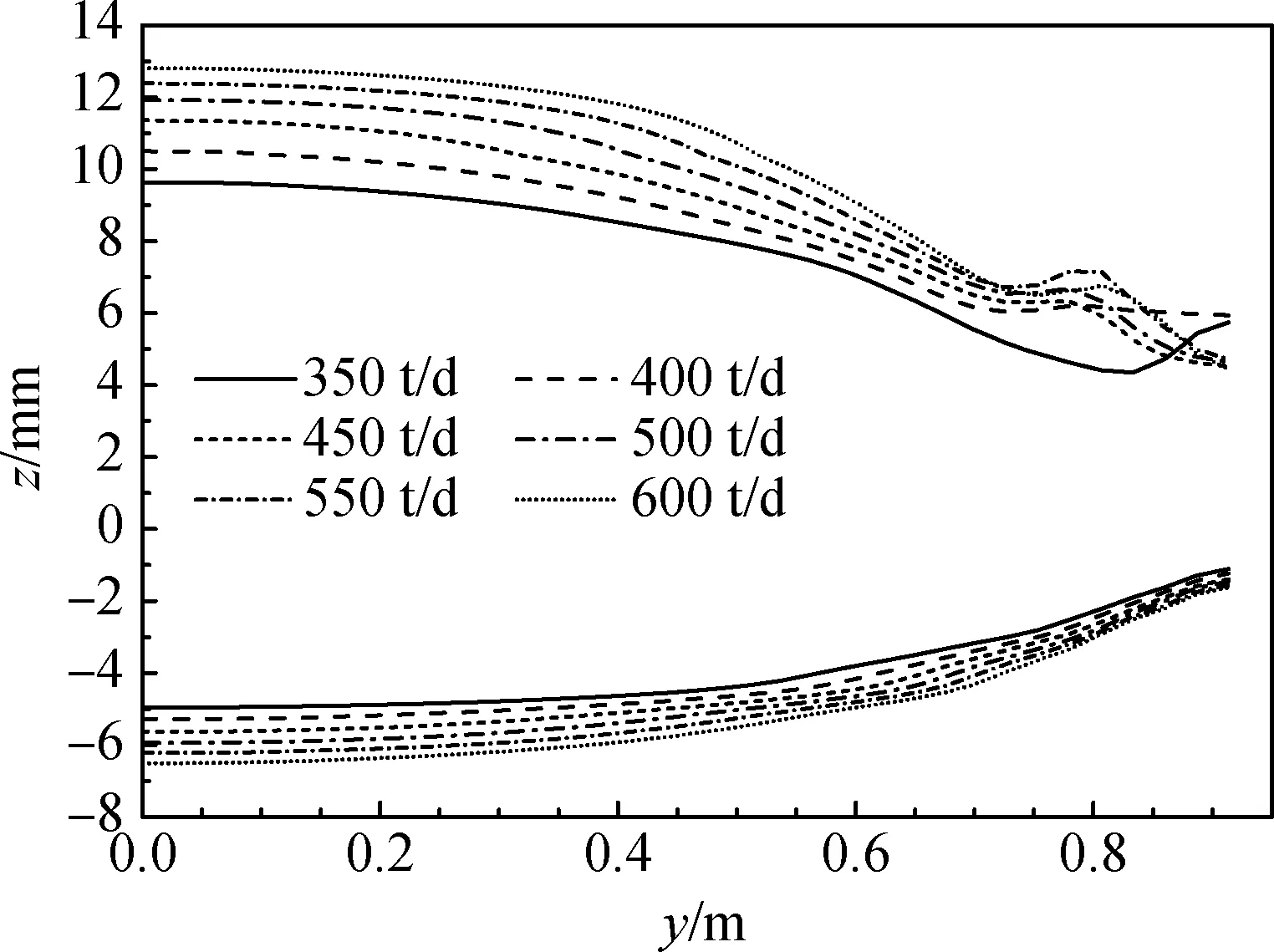
图15 不同拉引量条件下出口截面处玻璃液轮廓
由厚度结果可知:当拉引量为350 t/d时,出口截面边缘处玻璃液出现较薄区域,当拉引量继续降低时,将导致玻璃液层出现破裂;而随着拉引量的提高,x=0.3 m截面处玻璃液层边部区域的液位差变大,表明玻璃液的横向铺展效果变差。因此,该锡槽的拉引量应控制在400~550 t/d范围内。
5 黏度对玻璃液成形过程的影响
锡槽内玻璃液呈层流状态,黏度对玻璃液流速影响显著。因此,本节模拟分析了拉引量为500 t/d条件下,黏度对玻璃液流动状态与成形过程的影响。
5.1 玻璃液成形过程
根据模拟结果发现,当黏度降低至100 Pa·s时,由唇砖流下的玻璃液流将卷入大量气体,造成液层断裂。因此,本文选取200~1 000 Pa·s黏度条件进行模拟分析。各黏度条件下,对称面处玻璃液的轮廓如图16所示。
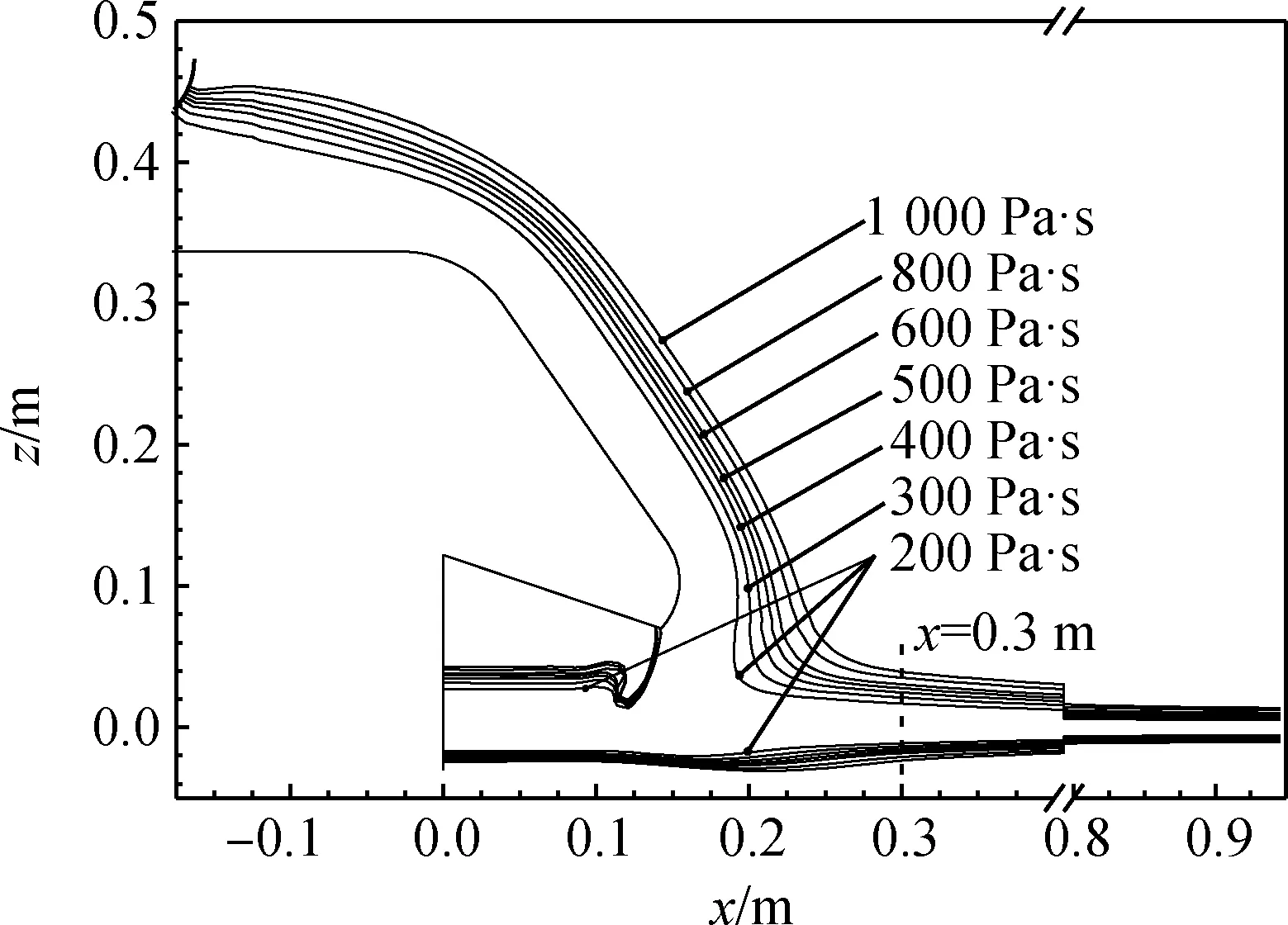
图16 不同黏度条件下对称面处玻璃液轮廓
图16所示结果表明:不同黏度下玻璃液的流动成形样式仍保持一致;而随着玻璃液黏度的增大,唇砖与锡液表面的玻璃液层均呈增厚趋势。此外,唇砖处玻璃液层厚度测量结果表明,黏度对液层厚度的影响规律满足式(10),结论与前文一致。
5.2 玻璃液厚度分布
计算得到八字砖区玻璃液的厚度分布,如图17所示。由结果可知,随着玻璃液黏度增加,八字砖区域内玻璃液层的厚度逐渐增加,且y方向的边部与中部玻璃液层厚度差呈变大趋势。不同截面位置的玻璃液厚度对比如图18、图19所示。
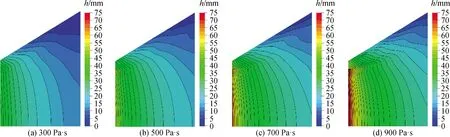
图17 不同黏度条件下玻璃液厚度分布对比
由图18、图19所示厚度对比结果可知:当黏度为200 Pa·s时,出口截面边缘处玻璃液厚度出现较大波动,主要由玻璃液流下时卷入一定量气泡进入边部所导致(如图20所示);当黏度继续降低时,玻璃液流唇砖下方玻璃液流卷入大量气体导致玻璃液层出现不连续;当黏度增大时,x=0.3 m截面处玻璃液层边部区域的厚度差显著增大,主要是由于玻璃液流动性变差,导致玻璃液的横向铺展效果变差。因此,有利于提高玻璃液层成形均匀性的黏度范围为400~600 Pa·s。

图18 不同黏度条件下x=0.3 m截面处玻璃液轮廓
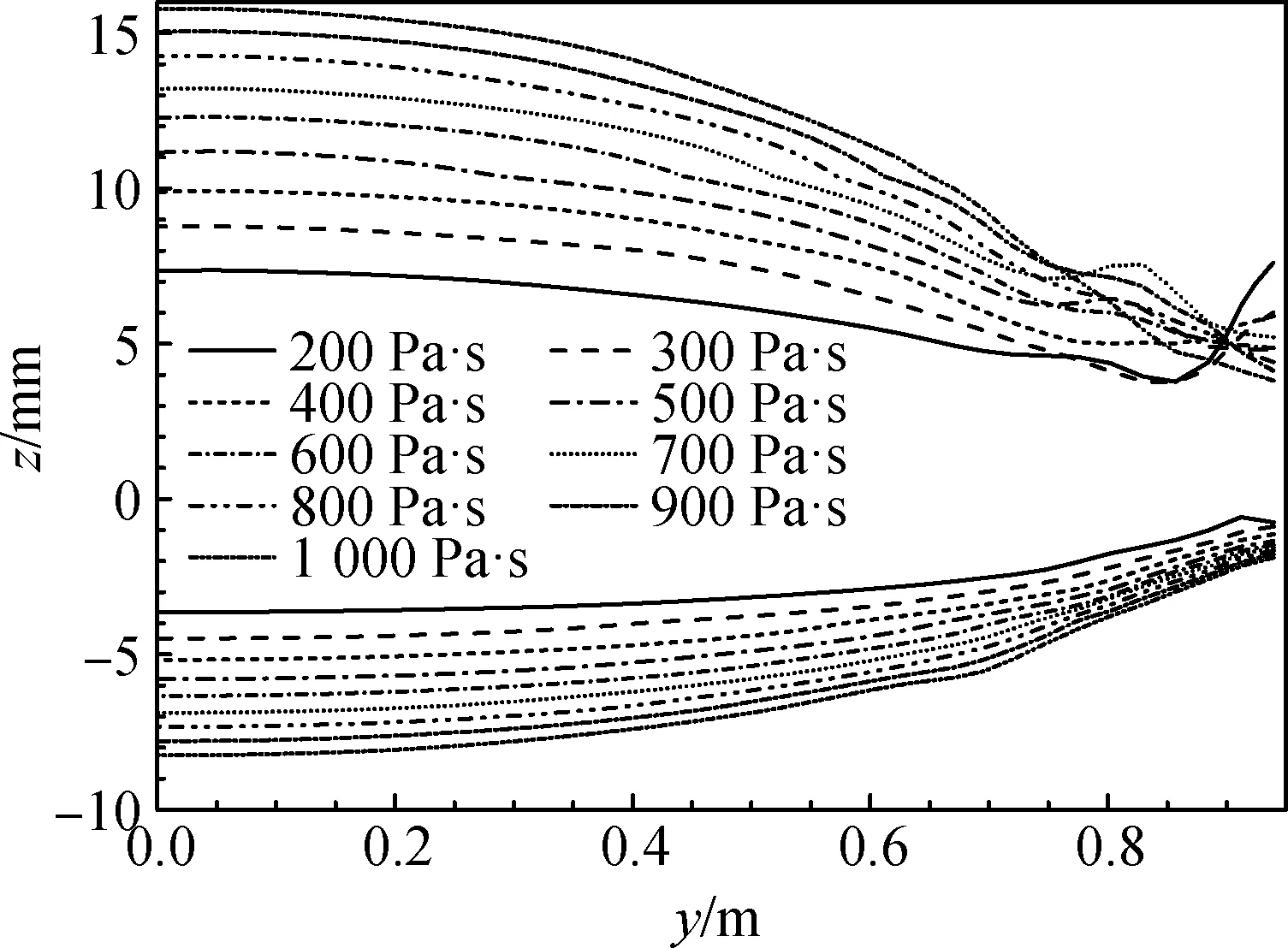
图19 不同黏度条件下出口截面处玻璃液轮廓
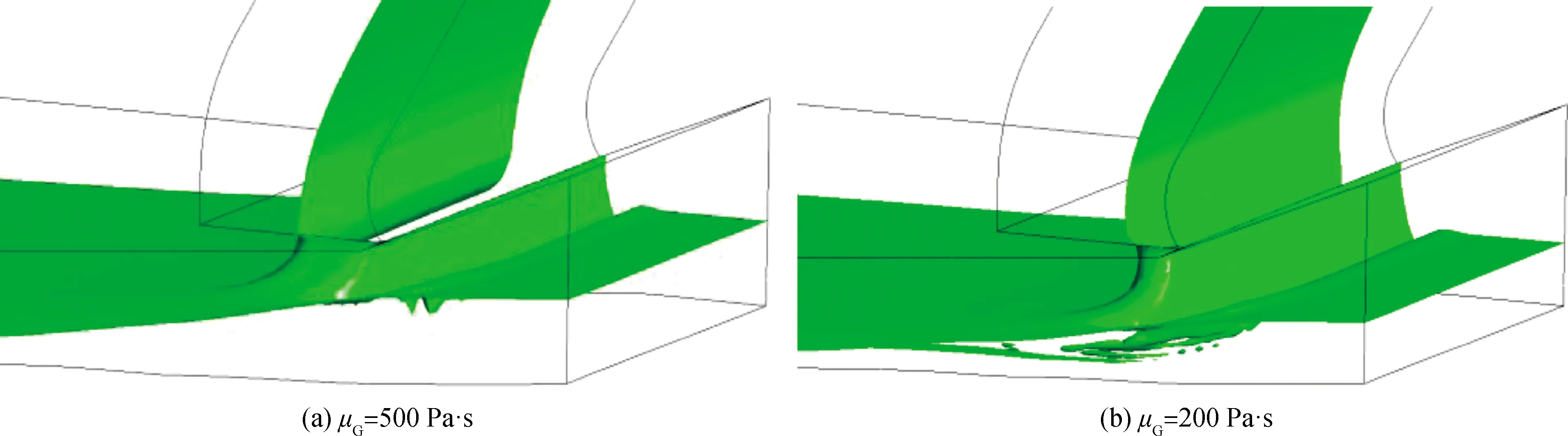
图20 不同黏度条件下唇砖处玻璃液-气氛界面
6 结 论
针对浮法玻璃成形工艺,提出了锡槽入口段简化稳态多相模型,采用Ansys Fluent 2019 R3软件对锡槽入口段玻璃液成形过程进行模拟分析。通过玻璃液平衡厚度验证模型,表明所建立的稳态多相模型可有效模拟玻璃液在锡液表面的铺展过程,为锡槽内玻璃液成形过程的研究提供了可靠手段。
利用所提出的简化稳态多相模型,对拉引量为500 t/d的普通浮法玻璃锡槽进行建模,模拟分析了拉引量、玻璃液黏度对锡槽入口段玻璃液成形过程的影响,结果表明:(1)拉引量低于350 t/d时,玻璃液无法充满八字砖出口,拉引量过高时,玻璃液层横向厚度均匀性变差;(2)黏度低于200 Pa·s时,唇砖流下的玻璃液流将卷入大量气体,黏度过高时,玻璃液流动性变差导致液层横向铺展变差;(3)案例锡槽实现浮法玻璃均匀稳定成形的工艺操作范围是拉引量400~550 t/d,黏度400~600 Pa·s,此时拉引量与黏度对玻璃液成形过程无显著影响。

