水泵水轮机在水轮机工况下转轮内不稳定流动及其演化

刘兵洋 ，杨 魏 ，王福军 ，刘竹青 ，黎耀军

（1.中国农业大学水利与土木工程学院，北京市 100083；2.北京市供水管网系统安全与节能工程技术研究中心，北京市 100083）

0 引言

水泵水轮机是抽水蓄能电站的核心部件[1]，其特有的S特性对机组的安全稳定运行造成了一定的不良影响。研究表明，该特性由水轮机制动工况转轮内部不稳定流动所造成的巨大损失所引起[2]。

近年来，国内外研究人员对S特性区内的不稳定流动作了大量的研究。Widmer等[3]人通过试验以及数值模拟，将S区内的不稳定流动划分为 Stationary vortex（固定涡）、Unsteady vortex（非定常涡）以及Rotating stall（旋转失速），并根据其各自压力脉动以及频率特征加以区分。ZHANG等[4]人在对水泵水轮机飞逸工况下无叶区压力波动转换机理的探索过程中，将S区内转轮内产生的涡结构分为FFVS（同主流方向传播的涡）和BFVS （回流涡）。但它们均未进一步阐述它们之间的相互关系。

为了进一步理解水泵水轮机S特性区转轮内不稳定流动产生的原因及演化机理，采用数值模拟的手段对水泵水轮机S特性附近工况转轮内的流场进行研究。

1 数值模拟方法

1.1 计算域与网格划分

选用某模型水泵水轮机的全流道作为计算域，如图1所示，部件包括蜗壳、固定导叶、活动导叶、转轮以及尾水管，为了减小尾水涡带对出口边界的影响，对尾水管出口进行延长。水泵水轮机的模型参数如表1所示，其中，ns为水轮机工况比转速，D1、D2分别为转轮低压边与高压边直径，Zb，Zgv和Zsv分别表示转轮叶片数、活动导叶数和固定导叶数，αmax表示导叶最大开度，计算活动导叶开度为20.03°。

图1 模型水泵水轮机计算域Figure 1 Computational domainof model pump turbine

表1 模型水泵水轮机几何尺寸Table 1 Parameters of the model pump-turbine

网格部分运用ANSYS ICEM对各过流部件进行结构化网格划分，为了保证捕捉到转轮内的流动分离，对近壁区网格进行加密，以保证转轮叶片表面平均y+<10。在保证转轮第一层网格高度不变的情况下，分别划分出网格节点数从201万到550万的5套网格，其水头相对误差如图2所示，从图中可以看出，当网格节点数达到320万时，水头波动减小到3%以内；此外，随着节点数的增多，叶片表面平均y+逐渐保持在3左右。因此，考虑到计算精度及叶片表面y+，最终选择网格节点数为320.67万进行后续计算。

图2 网格无关性分析Figure 2 Mesh independence analysis

1.2 湍流模型及边界条件

采用商业软件ANSYS CFX进行流场计算，定常计算采用SST k-ω湍流模型，非定常计算采用基于SST k-ω的DES（Detached Eddy Simulation）湍流模型。该模型结合了RANS和LES的优点，其主要思想是通过建立函数来改变不同位置处的湍流长度尺度，最终达到在壁面附近求解雷诺平均N-S方程，在远离壁面的主流区采用大涡模拟的算法。这样既能在近壁面发挥雷诺平均法计算量小的优点，也能避免高雷诺数下大涡模拟对网格要求太高的缺点[5]。现有研究表明，DES湍流模型在流体机械中存在大分离的流动中能够取得很好的结果[6]。

边界条件：在蜗壳进口设置质量流量边界，尾水管出口设置为静压边界。固体壁面设置为无滑移壁面条件。动静交界面在定常计算中采用Frozen Rotor，在非定常设置中动静交接壁面设置为Transient Rotor Stator，即滑移网格壁面。设置转轮每旋转1°的时间为一个时间步，每步收敛残差标准RMS=10-5，最大迭代步数为20步，共计算15个周期。

1.3 监测点设置

为了分析流场内的压力脉动特征，在流场的特定位置布置监测点。其中，在活动导叶中部以及固定导叶中部各布置一个监测点，活动导叶与转轮之间的无叶区沿周向布置20个压力监测点，即圆周方向每18°布置一个，此外，在转轮通道中沿径向依次布置3个压力监测点，监测点位置如图3所示。

图3 监测点位置示意图Figure 3 Schematic diagram of monitoring points

2 结果与分析

为了得到模型水泵水轮机内部压力脉动以及涡结构的演化，对20.03°导叶开度的10个工况点进行模拟计算。图4是试验与数值模拟结果对比图，其中，n11为单位转速，Q11为单位流量，按照式（1）、式（2）定义。

图4 S特性曲线试验与模拟比较Figure 4 Comparisons between the experimental and numerical characteristic curves

式中：n——转轮转速，r/min；

Q——质量流量，kg/s；

D1——转轮低压边直径，m；

H——水轮机水头，m。

在图4中，OP.1～OP.7位于水轮机工况，OP.8～OP.10位于水轮机制动工况。OP.7和OP.8分别位于飞逸工况两侧，在水轮机制动工况OP.8水轮机特性曲线表现为正斜率。可以看出，由CFD模拟出的结果与实验结果基本吻合，单位转速n11和单位流量Q11的误差均在3%以内。由此可以得出，本研究采用的数值模拟方法是可靠的。

2.1 压力脉动特征

为了获得水泵水轮机在水轮机工况以及水轮机制动工况的主要流动特征，对工况点OP.2、OP.5、OP.7和OP.8的压力脉动特征进行分析。4个工况点的详细参数及所处工况如表2所示。

表2 工况点参数（试验）Table 2 Operating parameters （experiment）

对采集到的压力信号进行无量纲化处理，用ΔH/H表示各监测点压力脉动峰值，其定义如式（3）所示。

式中：pi——瞬时压力值，Pa；

p1——蜗壳进口压力，Pa；

ρ——密度，一般取1000kg/m3；

g——常量，一般取9.8N/kg；

H——各工况水头模拟值。

图5显示了工况点OP.5和OP.8的固定导叶、活动导叶、无叶区、转轮进口压力脉动峰值。从图5（a）可以看出，随着流量减小，在水轮机工况也会出现较大压力波动，其中，转轮内的压力脉动幅值最大，无叶区次之。在水轮机制动工况，如图5（b）所示，除转轮区域外，其余流道各处的压力脉动幅值均不同程度增加，无叶区增幅最大，受转轮及无叶区影响，活动导叶内压力脉动幅度也逐渐增加。可以看出，随着工况点偏离最优工况，水泵水轮机的流动不稳定现象首先集中在转轮中，随着工况点进入水轮机制动工况，无叶区及活动导叶内不稳定流动现象随之加剧。

图5 不同工况压力脉动时域图Figure 5 Pressure fluctuation under different operating mode

图6 表示不同工况无叶区的压力信号时域图以及频域图。从时域图可以看出，随着流量减小，无叶区的压力脉动幅值逐渐增加，也变得更加无序。频率特性表明，在所有工况均出现了9fn的叶片频率（fn为叶片旋转频率）及其他由动静干涉引起的倍频。在水轮机制动工况OP.8出现了0.57fn的低频成分，且表现为主频，这说明在水轮机制动工况，除了动静干涉外，其他因素也引起了无叶区空间的压力波动。为了进一步研究该波动形成原因，需要进一步对转轮内的流动特征进行分析。

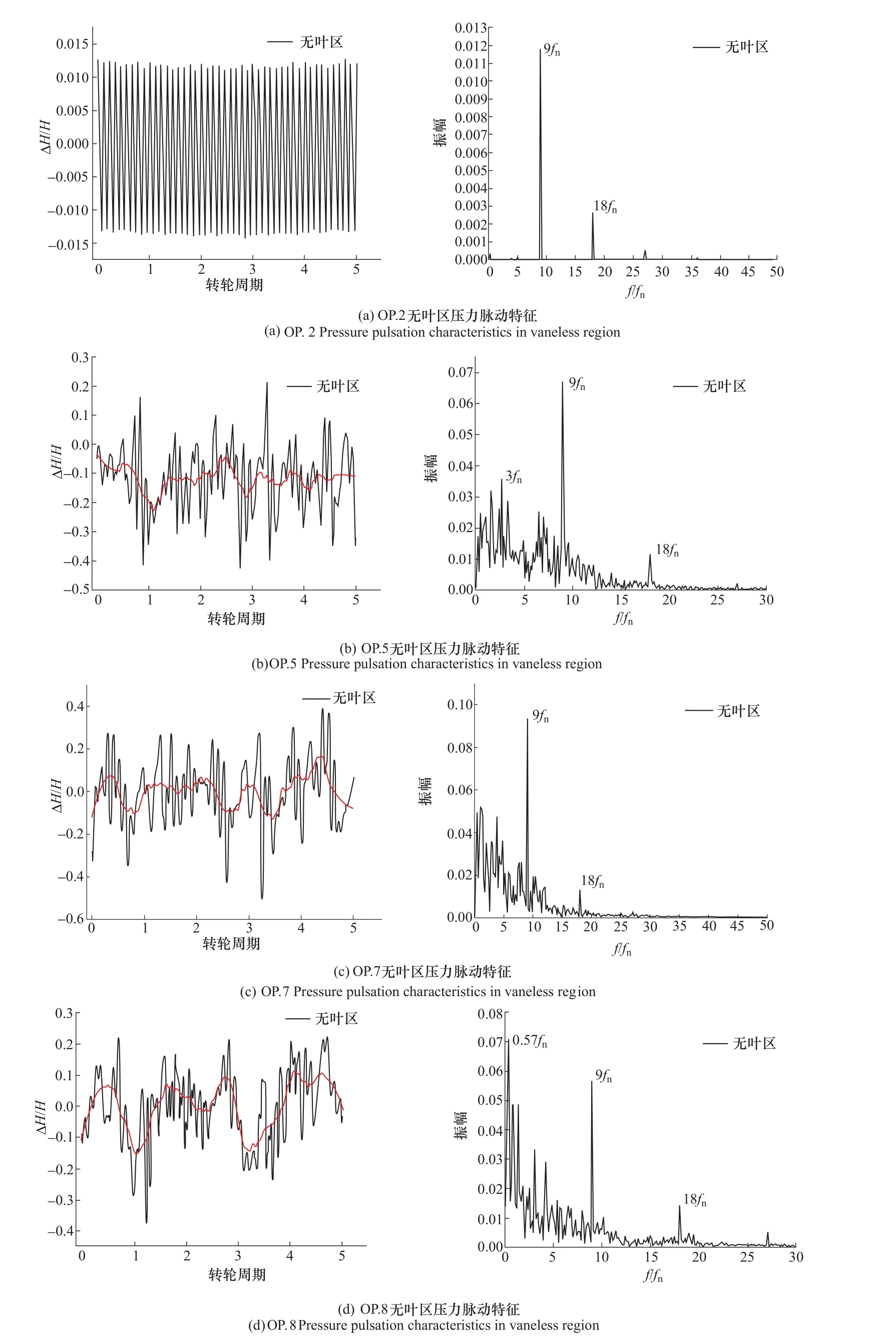
图6 不同工况无叶区压力脉动特征Figure 6 Pressure fluctuation in vaneless space under different mode

2.2 转轮内流态分析

现有研究表明[7]，在较大导叶开度的S特性区内，转轮内部会出现非定常涡以及旋转失速[8]，本节基于对这两个不稳定特征的捕捉，进而描述其主要特征及主要影响。

2.2.1 非定常涡

图7 为工况点OP.5、OP.7和OP.8的转轮进口的压力脉动特征。3个工况点的主频及振幅如表3所示。图8～图10是对应3个工况为0.9、0.5以及0.1叶轮展向位置处的流线图。流线图表明，在工况点OP.5，涡结构主要靠近hub侧，即0.1倍叶轮展向位置；且在所有叶片通道中都存在有涡结构，涡结构并未完全阻塞流道，也未出现明显回流，该涡结构未对上游流场产生明显影响。结合频域图可以得出，0.2fn的压力波动主要由此刻转轮内的涡结构演化所造成，该涡结构与Widmer等人[3]所描述的非定常涡特征相同。

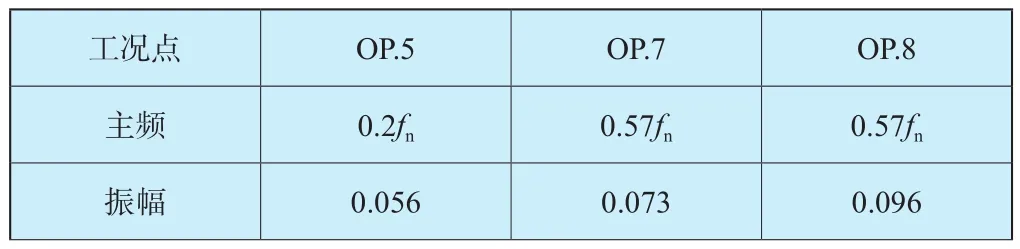
表3 不同工况频域信息Table 3 Frequency domain under different mode

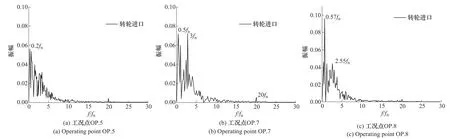
图7 不同工况转轮进口频域图Figure 7 Frequency domain on runner inlet under different conditions

图8 工况OP.5 各展向流线图Figure 8 Streamline distributions under OP.5

图9 工况OP.7 各展向流线图Figure 9 Streamline distributions under OP.7

图10 工况OP.8 各展向流线图Figure 10 Streamline distributions under OP.8

2.2.2 旋转失速

与工况OP.5相比，工况OP.7和工况点OP.8均出现0.57fn的频率成分，且对应压力脉动幅值更高，在工况OP.8表现为主频。通过流线图9和图10可以看出，在两个工况点转轮通道内的涡结构都呈现出明显的非对称性，仅存在于连续的几个流道当中，且在部分流道造成阻塞以及回流。尤其在工况点OP.8中，叶道内涡的非对称分布更加明显，流道被严重阻塞，回流增加，并对无叶区及上游流场产生影响，即转轮内出现旋转失速。

此外，在工况点OP.7和OP.8，涡结构在靠近hub侧（0.1倍转轮展向）最明显，因此，用hub侧的流线图进一步分析旋转失速传播特征。图11是工况点OP.8从时刻t1开始每隔一个转轮周期T的流线图（hub侧），红线表示失速团所在流道。从图中可以看出，涡结构在叶片通道中沿旋转方向，以小于叶轮转速的速度传播。

图11 工况点OP.8流线图（0.1span）Figure 11 Streamline distributions under OP.8（0.1span）

图12 是工况点OP.8无叶区监测点的压力脉动时域图，从图中可以很明显看出，在无叶区的压力脉动在该工况呈现出周期性，在7个周期内出现了约4次压力波动，传播周期约为1.75倍的转轮旋转周期，此传播周期与该工况无叶区0.57fn特征频率相佐证。

图12 工况点OP.8无叶区压力脉动时域图Figure 12 Time history of pressure fluctuation in vaneless space under OP.8

综上可知，沿20.03°等开度线，从水轮机工况到水轮机制动工况，转轮内先后出现了非定常涡以及旋转失速。其中，非定常涡沿周向分布在所有流道，旋转失速沿转轮周向非对称分布，存在于连续的几个流道当中，并以亚同步转速在流道中传播，失速团在正斜率工况（OP.8）的叶片通道中发展完全。

2.3 转轮内不稳定流动转化过程

图13是工况点OP.5和OP.8某时刻各叶片通道流量图，其对应的x轴表示转轮的9个叶片通道，y轴表示该时刻瞬时流量Q与叶片平均流量（Qav）的比值。可以看出在工况点OP.5，受非定常涡沿周向分布，各叶片通道的流量均出现了不同程度的波动，但未造成明显的通道阻塞现象。在工况点OP.7，部分流道发生阻塞，但阻塞的流道位置随机。然而，在工况点OP.8，受旋转失速影响，流道中的涡结构已经进入稳定的周期旋转模式，通道阻塞现象表现出连续性，即在相邻的3个流道（流道9、1、2）流量均明显偏离平均流量。图14是OP.8对应时刻的流线图，可以观察到在对应的3个流道均出现了发展完全的失速团。

图13 不同工况各叶片通道流量分布图Figure 13 Flow distribution of each blade channel under different conditions

图14 工况点OP.8流线图（0.5span）Figure 14 Streamline distributions under OP.8（0.5span）

对转轮内部流场进行进一步分析发现，转轮中涡结构的转化与叶片通道的流量变化密切相关。即随着流量的减小，叶片通道的阻塞驱动了非定常涡逐渐表现出稳定的周期性旋转模式。如图15所示，由于流量减小，入流角与叶片安放角存在一定冲角，导致水流冲击叶片面之后向吸力面偏移，在吸力面形成扰流并最终在流道中产生非定常涡结构，在所有流道均出现了几乎相同的现象。随着流量进一步减小，涡结构进一步发展，部分流道出现阻塞现象但分布随机。如图16所示，某一流道的阻塞会造成流体向相邻流道流动，当受阻塞流体流入与旋转方向相同的相邻流道时，会冲击叶片的吸力面，从而抑制该流道吸力面的涡结构。然而，在与旋转方向相反的相邻流道，受阻塞流体的流入会加剧水流冲击叶片的压力面，进而在叶片背面产生更强的涡结构。也就是在这样的相互作用下，随着流量的降低，不稳定涡结构逐渐展现出稳定的周向传播模式，即旋转失速。

图15 非定常涡形成机理示意图Figure 15 Formation mechanism of unsteady vortex

图16 旋转失速形成机理示意图Figure 16 Formation mechanism of rotating stall

旋转失速由转轮中的非定常涡发展而来，随着流量的降低，转轮通道中形成非定常涡结构，当某一流道的涡结构增加导致通道阻塞时，会逐渐驱动不稳定涡沿与转轮旋转相反的方向传播，并最终表现出稳定的周期性特征同时阻塞流道，即发展为旋转失速。

3 结论

本文以模型水泵水轮机为研究对象，通过数值模拟方法，分析了水泵水轮机S特性区附近工况转轮内的主要不稳定特征及其演化机理。主要结论如下：

沿等开度线，转轮中依次形成非定常涡和旋转失速。其中，旋转失速表现出稳定的周期性特征，失速团造成通道严重阻塞，并以亚同步转速在叶片通道内传播。分析表明：旋转失速由转轮内的不稳定涡结构发展而来，涡结构发展造成的部分叶片通道阻塞促使了这一转化过程。

在本次模拟中，旋转失速在特性曲线“正斜率”处充分发展，因此，进一步明确了旋转失速与“正斜率”产生的关系，对削弱机组“S特性”有重要参考价值。