机电引信滚动轴承外圈局部磨损间隙故障建模方法

武 澎，王 森，马 兵，井会锁，刘 奇

(西安机电信息技术研究所，陕西 西安710065)

0 引言

在机电引信设计过程中，由于滚动轴承具有功率消耗小、精度高、结构紧凑等优点，将其作为旋转运动的重要支撑部件。在运动过程中，滚动轴承常常出现不同形式的故障从而影响其工作的稳定性，有时甚至发生磨损故障影响机电引信作用的可靠性。

早期滚动轴承故障分析都是基于平常试验中的检测和总结得来的。最近几年，国内外的众多科研工作者应用非线性动力学的理论与方法，对滚动轴承的故障机理进行了比较深入的研究。在滚动轴承故障的建模分析方面，文献[1]分析了机匣滚动轴承耦合时系统故障的动力学模型和系统行为。文献[2—3]研究建立了滚动体有点蚀磨损时的滚动轴承故障模型。文献[4]分析建立了内圈有点蚀磨损时的滚动轴承故障模型。然而数学模型的建立，只是滚动轴承故障情况下动力学响应相关研究的开始。文献[5—6]提出了一种数值分析方法，利用这种方法可以去预测分析滚动轴承中滚动体上出现故障后对于转子系统振动的影响。文献[7]建立了滚动轴承内圈出现局部故障的动力学模型，将轴承的磨损间隙深度作为接触变形量，对故障后转子存在预负载荷情况下系统的动力学响应做了相关的研究。也有大量的国内学者，对滚动轴承出现故障的情况进行了建模以及仿真分析：例如文献[8]建立了滚动轴承磨损间隙故障的动力学模型，利用ANSYS将接触变形从瞬间模型修正为渐变模型，并在此基础上利用对系统的动力学行为进行了仿真分析。基于故障轴承的动力学分析，将轴承磨损间隙的深度作为接触变形量与实际工况是不相符的，接触变形量是需要精确判定和计算的。针对滚动轴承外圈局部磨损间隙故障模型中，将轴承外圈磨损间隙深度作为接触变形量不符合实际工况的问题，提出利用外圈故障轴承接触变形量的判定条件及表达式为基础进行建模的方法。

1 滚动轴承故障分析原理

由非线性轴承力的计算可以知道，轴承未出现故障的情况下，滚动轴承的接触变形ui[9]可表示为:

ui=xsinθi+ycosθi-γ0。

第i个滚珠的非线性恢复力fi为：

(1)

式(1)中，下标“+”表示只计算括号内为正数时候的数值，如果括号内的表达式为负值或者0，则取fi=0。

设损伤为一凹坑，形状为一球缺，其横截面即为损伤表面，2a为损伤表面的直径，Cd为损伤的深度。对于滚动轴承，点蚀、破损会出现在三种位置，内圈、外圈和滚动体上。滚动体磨损间隙滚过套圈时，接触变形的释放是由滚动体向套圈破损位置释放或者是套圈向滚动体磨损间隙中释放。且对于不同位置的点蚀和破损，滚动体在和磨损部位接触的时候，由于内外圈的滚道直径的不同，以及滚动体与内外圈接触时候的实际情况，都会引起套圈释放变形的不同，需要单独考虑出现不同磨损时候的变形量。而且简简单单的将磨损间隙的深度当做接触副释放的变形量来进行计算，显然也与实际情况不相符合。

总体上来说，当滚动轴承出现磨损的时候，滚动体经过磨损位置时候接触释放的变形量可以表示为：

ui=xsinθi+ycosθi-γ0-Δs，

(2)

式(2)中，Δs表示的是滚动体经过磨损位置时，套圈所释放的额外变形量。

2 滚动轴承外圈局部磨损间隙故障建模方法

机电引信因使用滚动轴承作为其旋转运动的重要支撑部件，其磨损故障模式为滚动体磨损故障、内圈磨损故障、外圈磨损故障。滚动轴承中，滚动体、内圈作为直接承载转子运动的部分，其磨损故障模型的建立及分析已经相对完善。外圈作为滚动轴承的重要组成部分，也应有其相应磨损故障模型的建立及分析。为此本文提出机电引信中滚动轴承外圈局部磨损间隙故障建模方法，并分析了外圈局部磨损故障对转子系统带来的影响。

2.1 外圈局部磨损间隙结构特征

外圈发生磨损故障的时候，磨损部位通常都是位于轴承的承载区域。轴承的承载区域如图1所示。

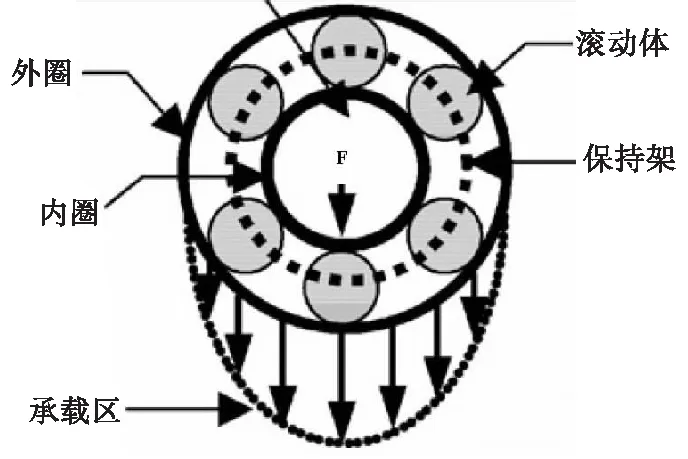
图1 滚动轴承承载区域示意图Fig.1 Schematic diagram of load distribution of the rolling bearing

当外圈具有单一局部磨损的时候，磨损间隙的几何模型如图2所示。

图2 外圈损伤示意图Fig.2 Spalldefinition on the outer race

图2中Cd为外圈损伤的径向深度，θdt为损伤的角宽度(损伤角跨度)，θdc为损伤角在外圈所处的角位置。由几何关系可以知道，滚珠在磨损间隙处是否形成冲击，并且滚珠和损伤部位接触的时候释放的额外的变形量都将取决于损伤直径和损伤径向深度之间的大小关系。将外圈的磨损间隙示意图展开，如图3所示。

图3 外圈损伤展开图Fig.3 The expansion plan of the spall on outer race

2.2 外圈局部磨损间隙故障建模

利用滚动轴承外圈故障的结构特征，给出故障轴承形成冲击振动的几何判定条件，得到滚动轴承外圈故障轴承间隙变化量的解析式，在此基础上通过已有的滚动轴承故障模型，得到外圈故障模型的解析式。

(3)

时滚动体与外圈的损伤接触时才可以形成冲击，否则将会产生谐波激振。事实上，滚动轴承外圈的局部磨损，特别是在早期的磨损面积通常都会比较小，基本上可以满足式(3)的条件，因此通常造成接触的额外磨损而形成冲击振动。为了研究分析方便，本文假设轴承外圈的局部磨损以及内圈磨损均满足式(3)，对轴承产生冲击力。

上边的判定条件从冲击振动的角度考虑了磨损间隙深度和可能的接触变形量之间的关系。为了从几何关系的角度精确地模拟外圈的局部磨损故障，这里认为当滚珠运动到局部损伤区域之后，轴承间隙与正常轴承相比会突然增加，可能导致该滚珠与轴承内外圈之间的非线性接触力突然降低或直接变为零，因此，需要准确地计算滚珠位于损伤区域时轴承间隙的额外变化量。实际上，有了式(3)的判定条件，我们可以得出当出现外圈故障时，由局部损伤引起的轴承间隙的额外变化量为：

Δs=Cd。

(4)

(5)

所以可以得出轴承间隙的变化量Δs表达式以及判定条件分别为：

(6)

式中，θdt=arcsin(2a/Ro)，Ro为轴承外圈直径。在计算非线性轴承力的过程中，只需要将轴承间隙变化量Δs代入式(2)中求解即可。

3 仿真验证

在机电引信中，滚动轴承通常被用作隔离转子的承重部件，其转动过程中的稳定性，对于隔离转子能否运动到位起着重要的作用。文章通过与无故障滚动轴承模型的仿真结果对比，验证所建立的滚动轴承外圈磨损间隙故障模型的有效性。

造成滚动轴承外圈出现磨损间隙的主要原因为轴承外圈与滚珠之间产生滚滑的现象。实际工况中，当轴承外圈与滚珠之间为纯滚动时，滚滑比ζ=0；当轴承外圈与滚珠之间为临近打滑的滚滑状态时，滚滑比ζ=0.3；为了便于仿真研究因滚滑带来的磨损间隙，选取滚滑比ζ=1>0.3，并给出其他相应的参数，滚动轴承的负载为F=60 N，滚珠的个数Nb=9，阻尼系数c=200 Ns/m，载荷变形系数Kb=7.055×109N/m3/2，外圈直径Ro=28.262 mm，内圈直径Ri=18.78 mm，滚珠直径为Rb=4.762 mm，半径间隙γ0=10-6m，X方向的偏心量ex=0 mm，Y方向的偏心量ey=0 mm。缺陷初始角位置θdc=0°，外圈磨损间隙的径向深度Cd=100 μm，磨损间隙直径2a=3 mm，则θdt为磨损的角宽度(损伤角跨度)，大小为θdt=arcsin(2a/Ro)。

图4所示为转速为ω=3 500 r/min时，外圈故障前后轴颈中心的动力学响应。从图4(a)和(b)的对比可以看出，正常轴承的轴承中心X方向的振幅为0.12 mm、Y方向为0.036 mm；故障轴承轴承轴承中心X方向的振幅为3.3 mm、Y方向为1.6 mm。即使出现轻微磨损，轴承的运动振幅也会大幅增加，运动也更加紊乱。图4(c)和(d)为正常轴承和故障轴承轴径中心X方向的振幅图，能够更加直观地看到X方向振幅的增加。图4(e)所示为轴承故障前后轴颈中心沿Y方向的速度变化对比图，可以看出，这个时候轴颈中心Y方向的速度波动比较大，沿Y正方向的速度值在一定的时间点上比负方向的速度值大，这也说明了轴颈中心在滚珠经过外圈磨损部位的时候垂直速度的突然增加。

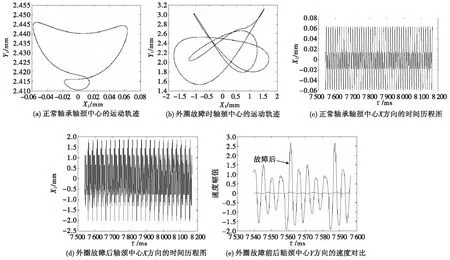
图4 ω=3 500 r/min时，外圈故障前后轴颈中心的动力学响应Fig.4 The response of the center of bearing journal between healthy bearing and bearing with defects on outer race for ω=3 500 r/min

图5所示为其他参数不变，当转速为ω=5 900 r/min时，外圈故障前后轴颈中心的动力学响应。可以看出，正常轴承轴承中心X方向的振幅为0.13 mm、Y方向为0.038 mm；故障轴承轴承轴承中心X方向的振幅为4 mm、Y方向为2.3 mm。由整个数值计算结果可以看出来，在滚动轴承外圈出现轻微的磨损故障后，滚动轴承转子系统的运动稳定性降低，相对于转速为ω=5 900 r/min时，故障轴承在转速为ω=5 900 r/min时轴颈中心的振幅进一步增大，运动更加不平稳。

通过上述仿真不难发现，故障轴承转子系统在转子腔体设计过程中，要将因滚动轴承磨损间隙引起的转子窜动的余量考虑在内，否则会出现转子转动过程中因间隙余量过小，转子窜动振幅过大卡死在腔体的现象，进而影响到机电引信工作的可靠性。

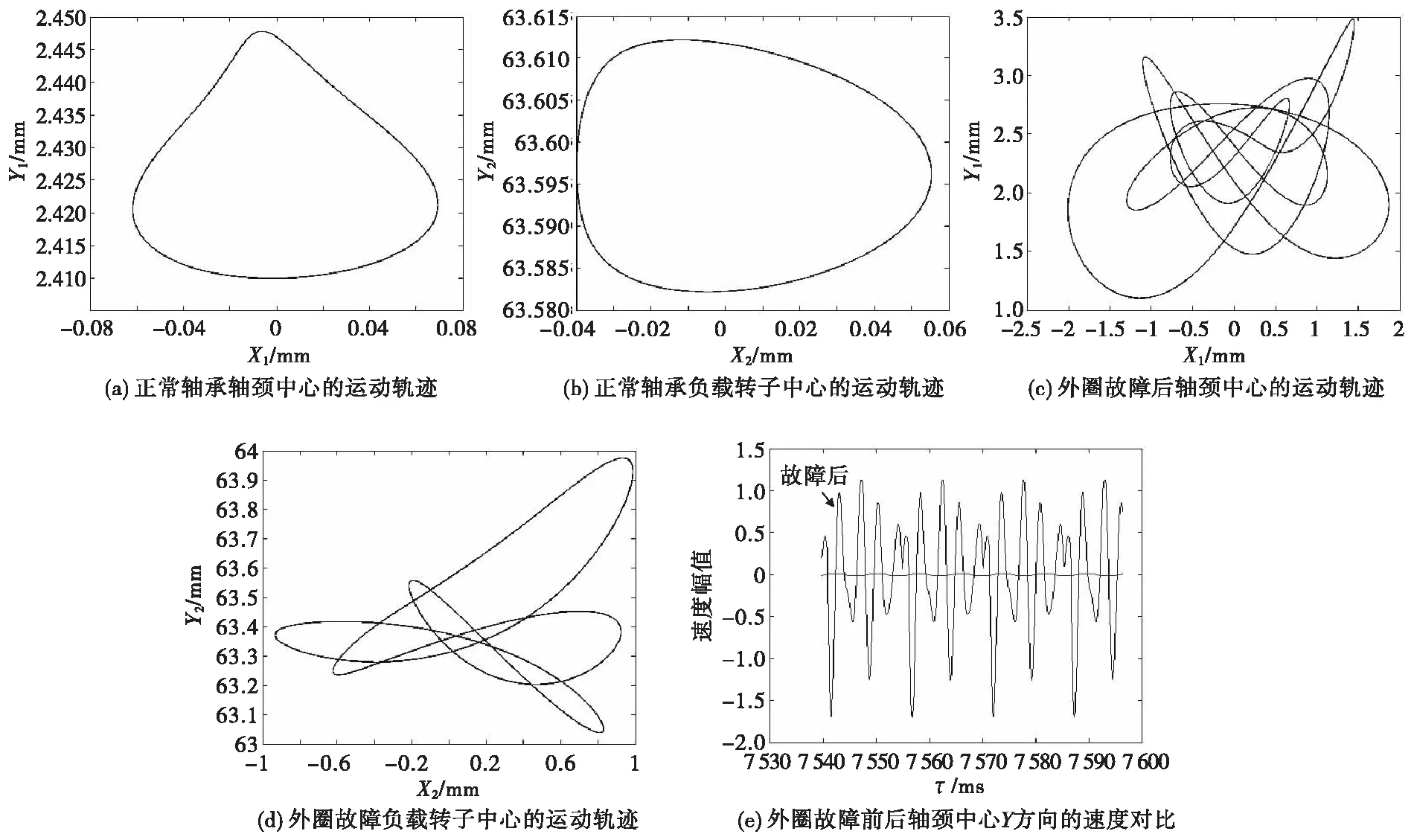
图5 ω=5900 r/min时，外圈故障前后轴颈中心的动力学响应Fig.5 The response of the center of bearing journal between healthy bearing and bearing with defects on outer race for ω=5900 r/min

4 结论

本文提出利用外圈故障轴承接触变形量的判定条件及表达式为基础进行建模的方法。该方法利用滚动轴承外圈局部磨损间隙的结构特征，给出了故障轴承的准确变形量及轴承力的计算方法，得到了滚动轴承外圈局部磨损间隙故障模型的解析式，在此基础上对故障模型解析式进行解析仿真。仿真对比结果表明该模型能准确反映出轴承外圈磨损故障后，故障轴承转子系统运动稳定性降低，并且随着转速的增大，转子系统运动振幅增大的同时，运动更加紊乱。本文给机电引信滚动轴承转子系统及转子腔体的设计提供了一定的理论仿真基础，但由于目前缺乏相应的试验及测试设备，暂时无法进行相应的工程实践验证。