基于FPGA的电机控制器设计与性能验证

高春伦，高文进，张 冀，王市伟，刘红蕾

（潍柴动力股份有限公司，山东潍坊 261061）

0 引言

中国承诺将于2030年前达到二氧化碳排放峰值，2060年前实现碳中和。碳达峰、碳中和的实现需要各行各业的深度参与，汽车碳排放是我国碳排放主要来源之一，新能源汽车行业的蓬勃发展无疑将助推这一目标的实现。新能源车的主要核心部件为电力供应系统、电机、电机控制器[1]，电机控制器是衔接电力供应系统与电机之间关键部件，高性能的电机控制器将显著提升新能源车的整体性能[2]。传统电机控制器采用DSP作为控制核心，随着对电机控制要求的提高，控制算法越加复杂，尤其是功能安全的需求，使得采用DSP电机控制出现CPU负载率过高的情况[3]，在高转速时出现响应滞后，性能降低的现象。为应对这种情况，特斯拉、宝马、大众等车企逐渐将现场可编程门阵列（Field Programmable Gate Array，FPGA）引进到控制器中，以提升控制器性能[4]。

国内外对基于FPGA的电机控制器做了大量研究。刘川等[5]设计搭建了DSP+FPGA的核心的控制单元，并仿真验证了其正确性与实用性，但未做台架实验；浙江大学邱建琪团队对电机控制有广泛而深入的研究，黄晓冬等[6]基于FPGA实现了电机控制的速度闭环系统，初步验证了FPGA用于电机控制器的可行性；Hoang Than等[7]实现了一种用于无传感器PMSM驱动的RBF-NN整定PI控制器；Mohammad等[8]设计了一种基于FPGA的时钟频率为30 MHz的电流PI控制器，经验证结果表明，执行时间为68 ns。

本文主要研究了永磁同步电机（Permanent mag⁃net synchronous motor，PMSM）空间电压矢量脉宽调制（Space vector pulse width modulation，SVPWM）技术，基于FPGA设计实现了SVPWM核心算法，最后利用实验台架验证了基于FPGA的电机控制器具有响应速度快、系统效率高等优势。

1 PMSM空间电压矢量控制原理

永磁同步电机因其动态响应好、低速下转矩大、定位精度高等优势，在新能源车上得到广泛应用[9]。空间矢量控制能够有效减小逆变器电压谐波损耗，且易于控制，是PMSM控制的最重要手段[10]。

分析建立PMSM的数学模型是实现空间电压矢量控制的基础，忽略电机磁滞损耗、涡流效应、磁场饱和效应、磁场的高次谐波，假设绕组电流均为正弦波[11]，则PMSM可通过Clark变换将定子abc坐标系转化为dq正交坐标系，进一步通过Park变换转换为dq轴旋转坐标系下的数学模型，其矢量图如图1所示。d轴与永磁体励磁磁通方向重合，q轴与d轴正交，其关系如图所示，且坐标系与转子同步旋转，实现了dq轴绕组的解耦，将各系数时变系统变为恒量系统，PMSM数学模型下的电压方程为：

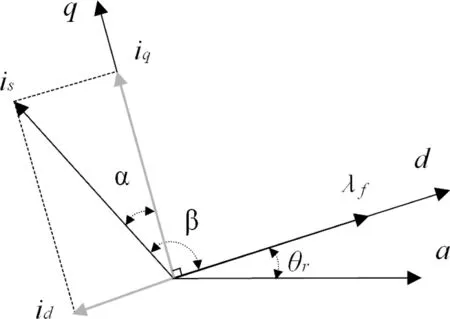
图1 PMSM旋转坐标系下的数学模型Fig.1 Mathematical model in PMSMrotatingcoordinatesystem

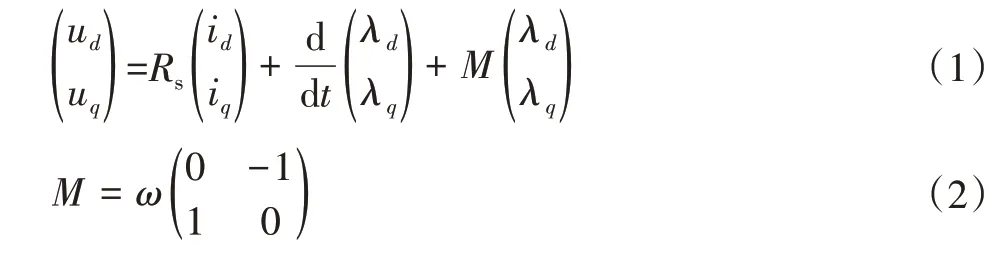
式中：ud、uq分别为定子电压在d轴、q轴上的投影分量；id、iq分别为定子电流在d轴、q轴上的投影分量；λd、λq分别为定子磁链在d轴、q轴上的投影分量；Rs为定子电阻；ω为电机转子电角速度。

磁链方程为：

式中：Ld、Lq分别为d轴、q轴上定子电感，即直轴电感、交轴电感；λf为永磁体磁链。

电机机械功率为：

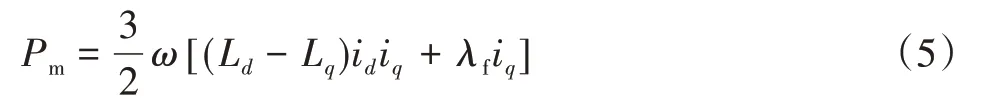
则PMSM输出转矩为：

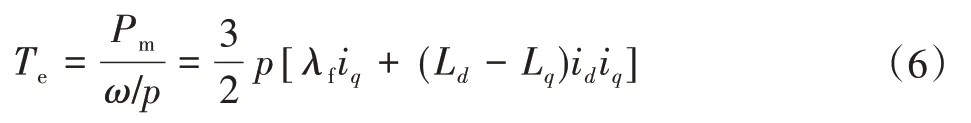
式中：p为电机极对数。

基于PMSM旋转坐标系下的数学模型，可建立PMSM空间矢量控制原理图，如图2所示。其基本原理是利用旋转坐标系下对d轴、q轴电流的控制实现对PMSM磁场与转矩的控制，d轴电流控制磁场，q轴电流控制转矩[12]。

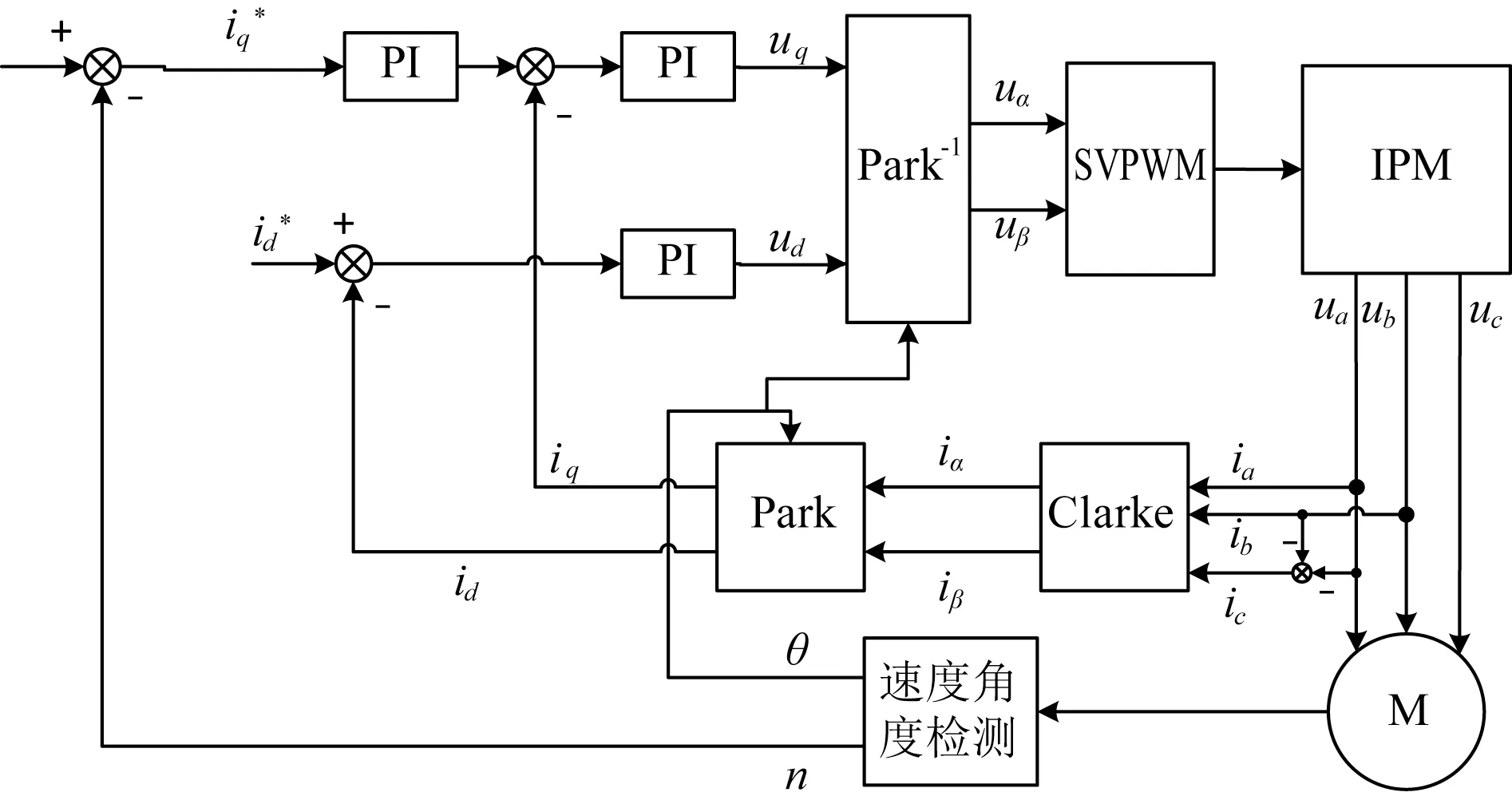
图2 PMSM矢量控制原理Fig.2 Principleof PMSMvector control

矢量控制的实现首先需基于目标扭矩计算旋转坐标系下设定d轴电流id*与q轴电流iq*，控制器根据电流传感器反馈的两相电流ia、ib或三相电流ia、ib、ic，经Clarke变换、Park变换得到旋转坐标系下的反馈电流iq、id。利用id、id*与iq、iq*，基于PI控制实现定子电流的闭环反馈控制，利用计算得出的uq、ud使反馈定子电流跟随设定定子电流。旋转坐标系下的dq轴电压通过Park逆变换转换为正交坐标系电压uα、uβ，经逆变器输出该电压对PMSM供电，实现矢量控制。

2 SVPWM的FPGA实现

FPGA因其并行的数据处理方式，可以同时处理多个运算模块，显著提高运算速度；具有框架灵活的特性，开发周期短，接口灵活；且FPGA技术发展迅速，其集成度更高，功耗降低[13]。矢量控制的FPGA实现采用Top-Down模块化的设计方式，其核心算法主要包括坐标变换模块、扇区判断模块、Cordic算法计算模块、矢量作用时间计算模块、PWM信号生成模块、死区模块等。其主要结构如图3所示。

图3 SVPWM算法结构Fig.3 SVPWMalgorithm structure

Cordic模块主要用于平方根计算与角度的正余弦计算。因为FPGA内部仅能直接实现加法与乘法，故需要通过迭代的方式实现。其实现思想为直角坐标系中初始点角度，通过n次迭代向所求点靠近，通过迭代点角度与目标角度之间的差值确定迭代方向，通过n次迭代，误差趋于0。

坐标变换模块涵盖第1节阐述的PMSM矢量控制坐标变换所需的Park变换模块、Park逆变换模块、Clarke变换模块。

扇区判断模块的作用是确定目标矢量在空间中的位置。扇区判断关系如表1所示。

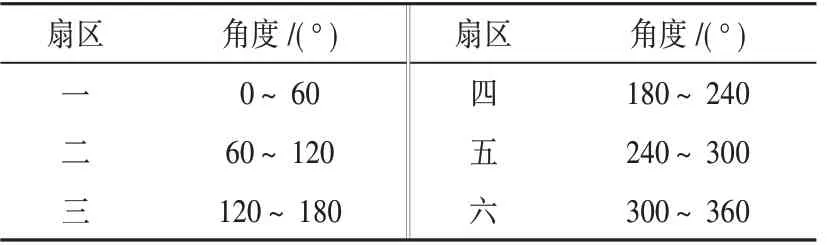
表1 扇区与角度关系Tab.1 Sector and Angle relationship

矢量作用时间计算模块可获得基本矢量作用时间，以用于矢量合成。根据空间矢量所处空间位置不同，其基本矢量作用时间不同，一、三、五区非零基本矢量作用时间为：

二、四、六区两个非零基本矢量作用时间为：

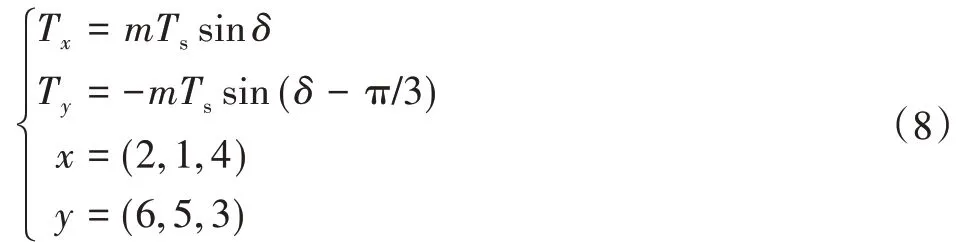
式中：Ts为PWM采样周期；m为调制系数；δ为d-q正交坐标系下，目标电压矢量与所处扇区起始边的夹角。

PWM信号生成模块采用七段式脉宽调制方法，每次仅有单个桥臂改变状态，降低开关损耗，减小IGBT发热，保证电机平稳运行。

死区时间模块的作用是防止IGBT相同桥臂上下桥臂同时非导通，故需要在PWM信号生成模块后加延时电路，产生死区时间，以防止短路，延时时长依据FPGA性能而定。其实现过程为，将坐标变换后得到的两正交电压矢量经反正切与平方根计算，输入到矢量作用时间计算模块与扇区判断模块，并将计算角度与位置检测环检测的电角度输入至扇区判断模块，输出目标电压矢量扇区与角度，经PWM信号生成模块生成六路PWM波，后经死区模块输出互补PWM信号。

3 台架实验

在同一台架按照GB/T 18488.2-2015电动汽车用电机及控制器测试标准对同一款永磁同步电机搭配以FPGA为核心的电机控制器与以DSP为核心的电机控制器分别进行扭矩响应与效率测试。结果表明，基于FPGA设计的电机控制器具备更优越的性能。

3.1 动态响应测试

对照组为DSP电机控制器匹配精进电机，实验组为FPGA电机控制器搭配同一款电机，台架ASM测功机参数为额定功率700 kW、最高转速6 000 r/min，搭配满足功率需求的功率分析仪与电池模拟器，恒温水冷系统冷却电机控制器、电机，使温度基本恒定，保证实验变量的唯一性。分别测试-500 N·m升扭矩至500 N·m，与500 N·m降扭矩至-500 N·m，通过台架记录响应时间，记录频率为1 000 Hz，部分结果如图4～7所示。处理数据如表2所示。

表2 扭矩响应时间测试Tab.2 Torqueresponsetimetest

图4 对照组400 r/min降扭响应测试Fig.4 Thecontrol group wastested for 400 r/min torquedrop response

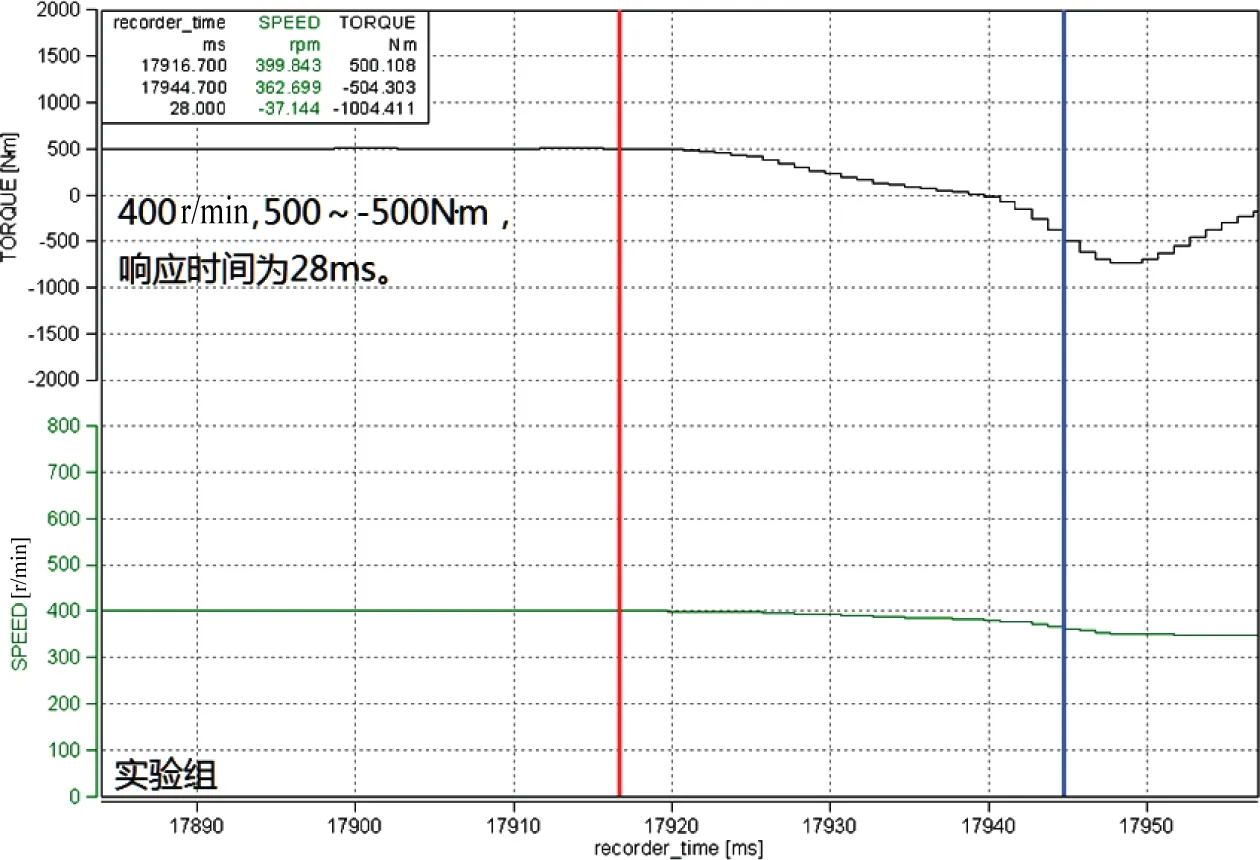
图5 实验组400 r/min降扭响应测试Fig.5 The experimental group was tested for 400 r/min drop torqueresponse

通过台架实验结果可知，FPGA控制器在不同转速下扭矩响应时间基本稳定在30 ms以内，响应速度明显优于以DSP为计算核心的控制器，响应速度提升25%～79%，且由测试结果，DSP电机控制器响应时间受工况影响大，不同工况下扭矩响应时间一致性差。

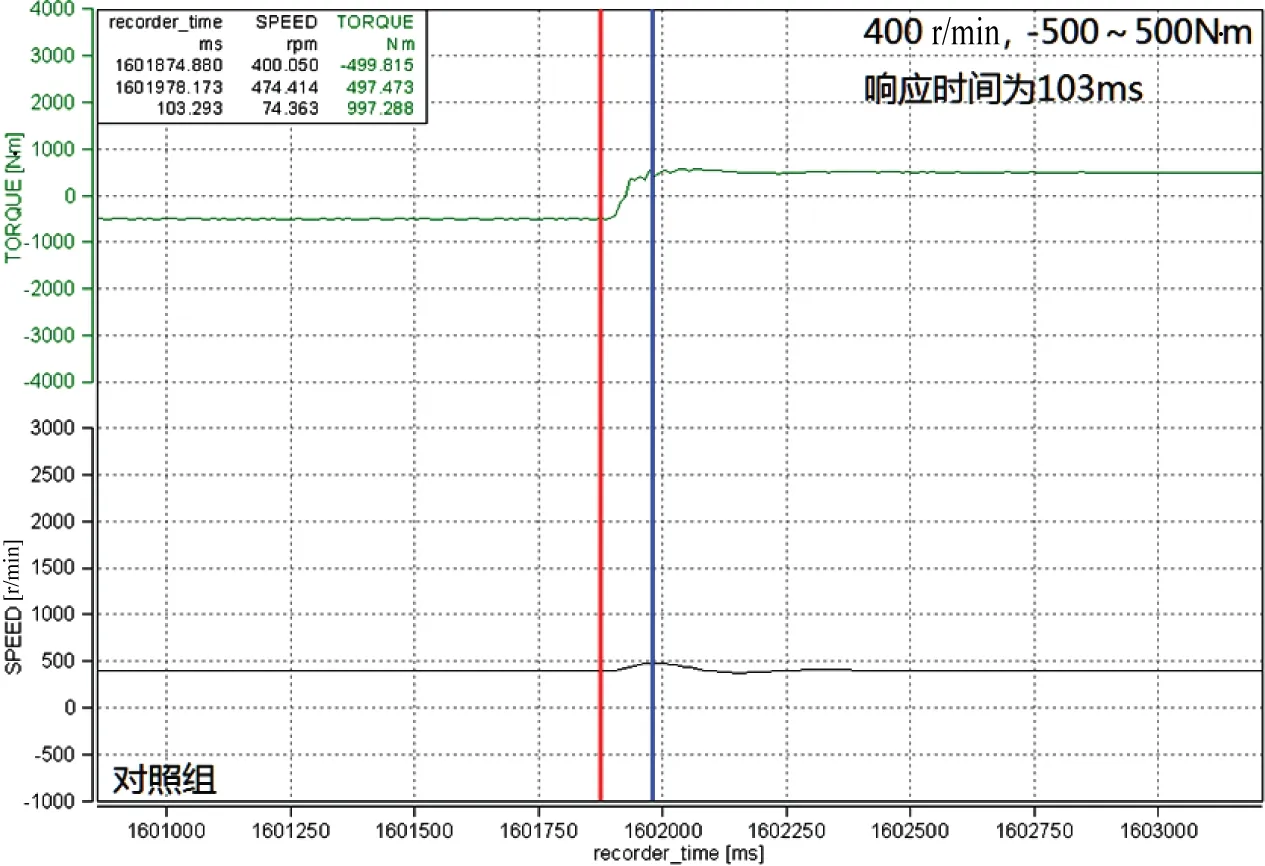
图6 对照组400 r/min升扭响应测试Fig.6 Thecontrol group wastested for 400 r/min lift-torsion response

图7 实验组400 r/min升扭响应测试Fig.7 Theexperimental group wastested for lift-torsion responseat 400 r/min

3.2 效率分析

对对照组、实验组分别测试相同工况系统效率，按照GB/T18488.2-2015，统计效率占比，结果如表3所示。由效率占比可知，基于FPGA的控制器提升了电驱动系统的整体效率，尤其是扩大了效率90%以上的高效区域。

表3 系统效率对比Tab.3 System efficiency comparison

4 结束语

本文研究了永磁同步电机空间电压矢量控制技术与以FPGA为核心的电机控制器设计实现。在详细阐述了永磁同步电机于旋转坐标系下的数学模型的基础上，分析了空间电压矢量脉宽调制SVPWM控制技术的原理，并基于此完成FPGA设计实现，最后利用实验台架分别测试了以DSP、FPGA为核心计算单元的电机控制器，以对比其性能。

通过实验验证，基于FPGA的电机控制器可用于永磁同步电机控制，且FPGA电机控制器具有扭矩响应快、动态性能好、提升驱动系统整体效率的作用，对于电机控制器设计与应用有重要的借鉴意义。