海工平台齿轮箱单元高速轴轴承热-结构仿真研究

马振军，余国轩，宋春生，徐天殷

（1.广东精铟海洋工程股份有限公司，广东佛山 528000；2.武汉理工大学，武汉 430000）

0 引言

目前，人类在经济、科技等方面都有了空前的发展，其中石油、天然气等不可再生能源的消耗量也在逐级增加，长时间地消耗陆地能源资源将面临开采储量不足的情况。然而在浩瀚的蓝色海洋中，蕴含着极为丰富的石油和天然气资源，开采利用海洋油气资源似乎已经成为了各国科学家们目前想到的可行可靠的解决陆地能源储量匮乏难题的重要手段。因此，海洋油气能源的开发近年来受到了极大地关注，如何开发海洋石油、天然气等资源也被各国纳入了发展规划中[1]。海洋工程中，自升式平台是在海上进行施工作业必不可少的大型海洋装备。

海工自升式平台升降系统齿轮箱单元是自升式海洋平台中一种必不可少的连接和传递动力的核心单元，起着至关重要的作用。而齿轮箱单元的高速轴轴承是整个齿轮箱单元的关键部件，拥有很好的承载能力和起动性能，是轴和其他转动机构的关键支承[2]。

一直以来，针对轴承寿命和精度的研究不断展开和深入，高速轴轴承的温度场分析和受热变形研究就是其中之一[3]。目前，关于轴承的温度场分析方法概括起来有试验测试法、热网络节点分析、有限元仿真模拟。第一种为试验研究，后两种为理论分析计算[4]。热网络分析法是把系统按着实际需求划分为若干热节点网络，每一个节点代表着相对应的温度值，依据能量守恒定理，通过求解相应的热传递模型就可以得出具体温度值[5-6]。有限元模拟仿真方法的求解思路是将研究系统划分为若干个网格单元，网格之间由节点连接，通过在节点中插入对应的分析函数，对离散方程进行求解得到所需要的值[7-8]。如今，比较成熟的有限元分析辅助软件有ABQUES、ANSYS等。

虽然关于滚动轴承温度场和热变形的研究已经比较成熟，但其研究方式和对象主要是针对与高速列车和一些其他重型机械，而针对于海工自升式平台升降系统的轴承热分析，目前还没有相关的成熟研究文献。因此，本文以海工自升式平台升降系统作为研究对象，通过有限元仿真的方式对其高速轴轴承进行稳态温度场分析以及热-结构耦合分析，为海工自升式平台升降系统轴承选择、寿命研究和热变形分析提供理论参考依据。

1 轴承热量产生及传递分析

1.1 轴承的生热分析

轴承内部聚集的热量主要是由工作轴承的内外圈与内部滚动体之间存在相对滑动导致摩擦产生的。而其余内部元件之间的摩擦、轴承正常旋转产生的阻力矩对轴承总的生热量影响比较小。所以轴承的摩擦力矩是轴承发热的首要因素[9]。

依据Palmgren经验公式可知[10]，滚动轴承在中等转速和中等载荷的工况下，总的摩擦力矩由与轴承类型、转速相关的摩擦力矩和载荷引起的摩擦力矩之和来确定，公式如下：

式中：M为与轴承中的总摩擦力矩；M1为与轴承载荷有关的摩擦力矩；M2为与轴承类型、转速相关的摩擦力矩。

式中：P1为轴承摩擦力矩的计算载荷，N；f1为与载荷和轴承型号有关的系数；dm为轴承的平均直径，mm。

P1与f1的选取如表1所示。值得注意的是，表1中P0为轴承当量静载荷；C0为轴承额定静载荷；y为轴向载荷系数。

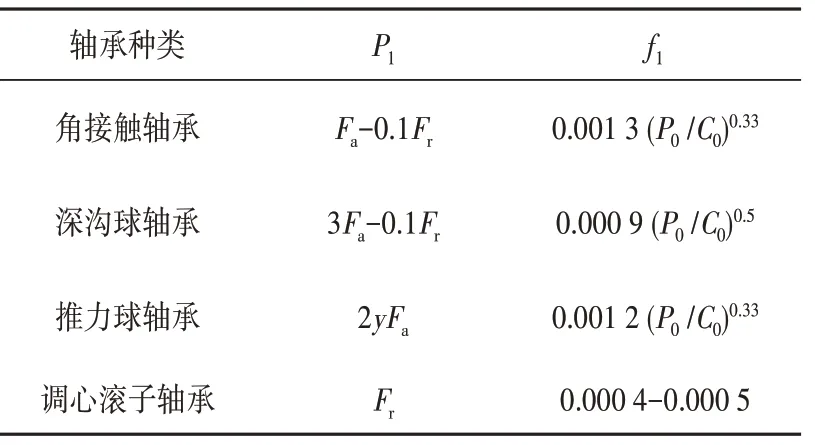
表1 P1与f1的计算数值Tab.1 Calculated valuesof P1 and f1

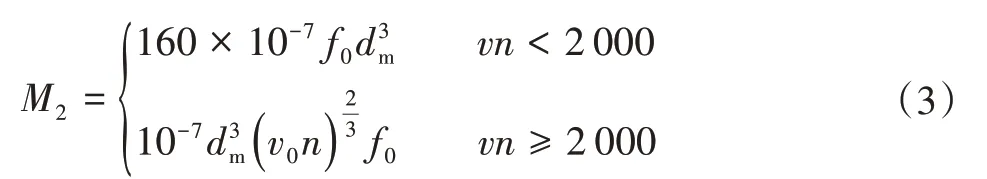
式中：f0为与轴承型号与润滑有关的系数，具体数值如表2所示；dm为轴承的平均直径，mm；v0为润滑油的运动黏度，mm2/s；n为轴承转速，r/min；

表2 选取轴承相关润滑系数Tab.2 Select the relevant lubrication coefficient of the bearing

轴承的摩擦功耗与滚动轴承中的摩擦力矩关系紧密，生热量和摩擦力矩的关系可表示为：

式中：H为轴承的生热量，W；M为与轴承中的总摩擦力矩，N·mm；n为轴承转速，r/min；轴承发热量最终按照1∶1在轴承滚动体和内外圈滚道上进行分配传递[11]。

上述把轴承作为整体进行分析的情况下，整理出的轴承摩擦力矩的计算方法，并没有触及轴承内部具体组件的功率耗损。

1.2 轴承热量传递分析

轴承传热形式主要包括3种，即热传导、热辐射和热对流。在轴承中，对流散热量是传导散热量的近20倍，表明轴承里产生的绝大部分的热量均由润滑液带走了，工作轴承中各组件表面与其周围润滑液之间发生的热对流是首要考虑的传热形式，在分析计算时基本可以忽略热辐射和热传导两种散热形式。

润滑液与轴承各零件表面的热对流可以表述为：

式中：H为工作轴承的发热量；T1为轴承零件表面温度值；T2为润滑油温度值；S为换热面积；h为零件表面与润滑油间对流换热系数，该对流换热系数受流体导热率、速度等因素的影响。

图1所示清晰显示了轴承座、轴和轴承中各个表面的对流换热边界条件。

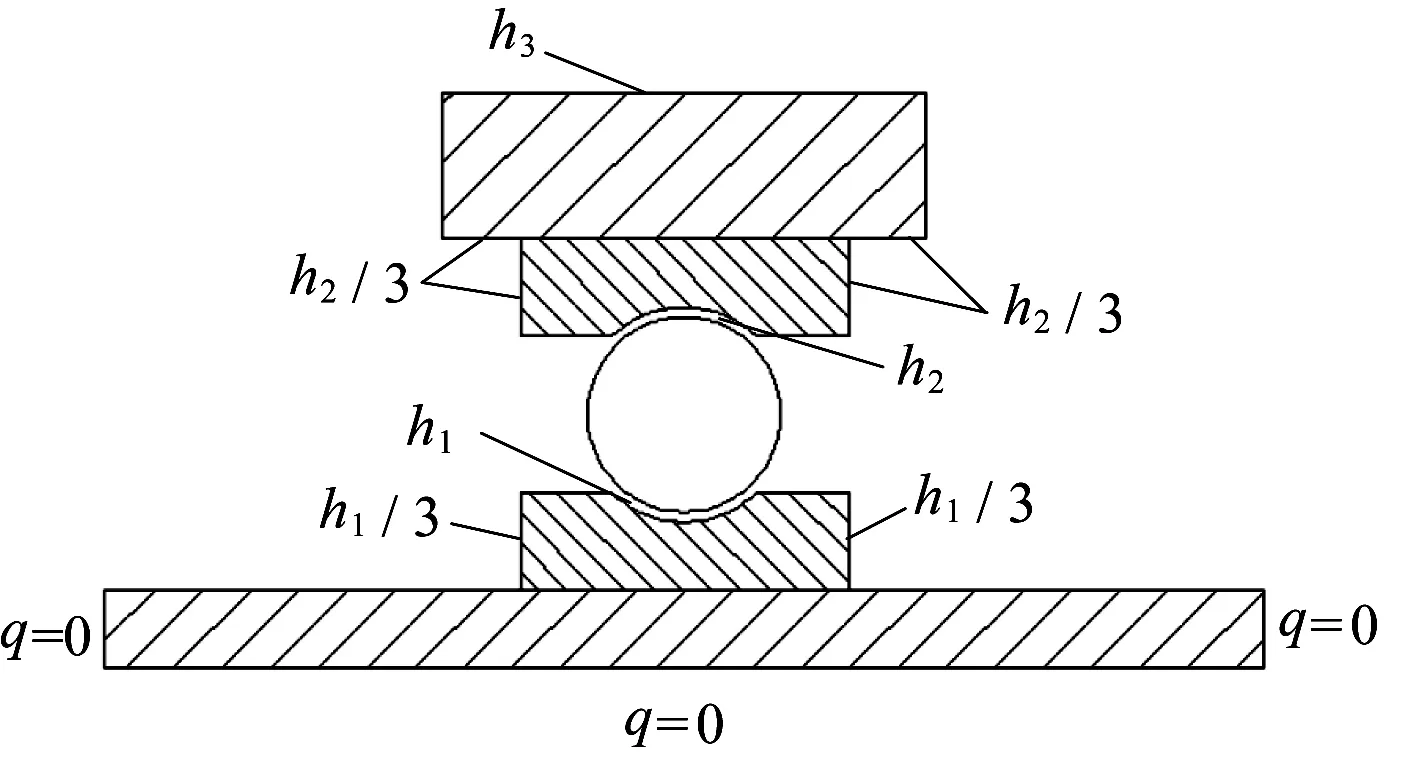
图1 轴承二维热分析模型简化示意图Fig.1 Simplified schematic diagram of bearing two-dimensional thermal analysis model

图1中，设轴承外圈表面的对流换热系数为h2，内圈表面的对流换热系数为h1，轴承内外圈表面的对流换热系数通过式（6）确定[12]：

式中：k为润滑油导热系数；Pr为润滑油的普朗特数；Re为雷诺数，Re=vx/v0，其中，v为钢球周向转速；x为特征长度，当计算滚动体向润滑液传热时，取x=dm，计算内圈向润滑液传热时，取x=di，计算外圈向润滑液传热时，取x=D；v0表示润滑油运动粘度。

轴承外圈端面的对流换热系数可以取h2/3；内圈端面的对流换热系数取h1/3[13]；轴承座外表面与箱体外空气的对流换热系数用h3表示，其计算公式为：

式（7）中：kα为空气导热系数；Dh为轴承座外表面直径；T表示轴承座外表面温度；Tα为环境温度。

式（8）中：vα为箱体外空气流动速度；μα表示空气的运动黏度。

2 轴承稳态温度场仿真分析

2.1 轴承工况及基本参数

某海工平台升降系统齿轮箱单元各轴承分布情况如图2～3所示。

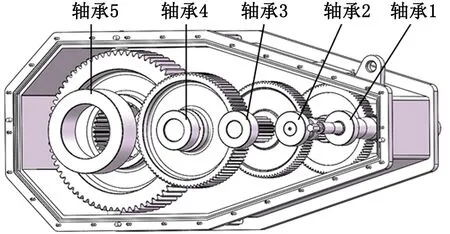
图2 海工平台平行齿轮箱轴承编号Fig.2 Bearingnumber of parallel gearbox of offshoreplatform

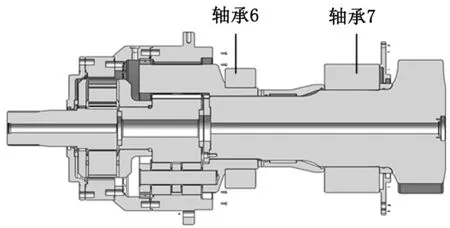
图3 海工平台行星齿轮箱轴承编号Fig.3 Bearingnumber of planetary gearbox of offshoreplatform

根据国内外海洋工程发展经验可知，海洋工程升降平台升降系统齿轮箱单元在工作时，平行齿轮箱高速轴部分是主要的故障部位；所以本文主要对海工平台中平行齿轮箱高速轴轴承1进行稳态温度场仿真分析和热变形仿真分析。

某海工平台高速轴轴承为深沟球轴承，型号为6411E。轴承材料均为CGr15，具体参数如表3所示。

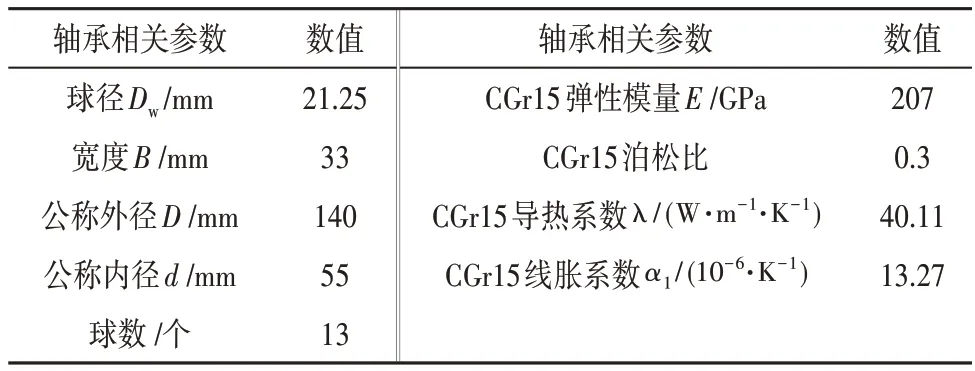
表3 深沟球轴承6411E相关参数Tab.3 Related parameters of ball bearing 6411E

2.2 轴承的有限元稳态热分析

通过Workbench的Steady-State Thermal模块对齿轮箱的高速轴轴承进行有限元分析，得到轴承在正常工况下以及不同转速下工作的温度场分布情况，并对所得到的有限元结果进行分析。

2.2.1 建立三维模型

在Solidworks中建立齿轮箱高速轴轴承的三维模型图，在建模时需要对轴承进行一定的简化：（1）消除轴承中的倒角以及倒圆角等微小结构；（2）忽略轴承的保持架。消除倒角和略去保持架之后可以使网格划分更加均匀和准确，使运算结果更为准确。建立完成的三维模型如图4所示。

图4 轴承6411E三维模型Fig.4 Three-dimensional model of bearing 6411E

2.2.2 定义材料、网格划分和建立接触对

在Engineering Data模块中选择新建CGr15材料，导热系数为40.11 W/(m·℃)。在Model模块Mesh选项中将滚动体的网格单元尺寸设置为2 mm，轴承内外圈的网格单元尺寸设置为5 mm，生成的有限元模型如图5所示。在Model模块Connections选项中建立有限元模型中所有的接触对。一般情况下，如果各部件之间开始时已经接触便会出现热传导，否则就不会发生热的传导。在计算轴承摩擦力矩时，“摩擦”因素已经考虑过，因此应该定义接触方式为“不分离”。

图5 轴承6411E网格划分Fig.5 Mesh division of bearing6411E

2.2.3 设置热边界条件

在对轴承对流换热系数和轴承生热量分析研究的基础上，给轴承模型施加热边界条件和热载荷进行分析。因为实际工况下高速轴轴承的径向载荷比较小，仅为820 N。远小于该轴承的额定静载荷，所产生的摩擦力矩对总摩擦力矩的影响较小，所以这里主要考虑黏性摩擦力矩M2对高速轴轴承生热量H的影响。轴承在正常工作下的生热量以及不同表面的对流换热系数如表4所示，将计算所得的生热量以及对流换热系数作为边界条件加载到轴承模型上。

表4 发热量及对流换热系数计算结果Tab.4 Calculation results of calorific value and convective heat transfer coefficient

2.2.4 有限元仿真结果分析

设置初始工作温度选为室温22℃，当海工平台升降系统稳定工作时，齿轮箱单元高速轴轴承的工作转速为1 518.6 r/min，轴承稳定状态时热分析结果如图6所示。由图可以看出：高速轴轴承在稳定运转的过程中，内圈与滚动体接触的位置温度最高，为52.337℃；外圈端面温度最低，为50.015℃。整体温度分布趋势为从内圈滚道到滚动体到外圈依次降低。所以，在进行轴承冷却和润滑方案设计时，要着重考虑轴承内圈和钢球接触区域的热影响，这样才能使轴承更好地散热、避免热疲劳的发生。

图6 轴承6411E稳态热分析结果Fig.6 Steady-statethermal analysis results of bearing6411E

3 轴承热-结构耦合分析

在对轴承进行热变形分析时，将海工升降平台齿轮箱单元高速轴轴承在稳定工作时的稳态温度场分布作为热边界条件加载在热-结构耦合分析中，在Ansys Work⁃bench中的操作如图7所示。

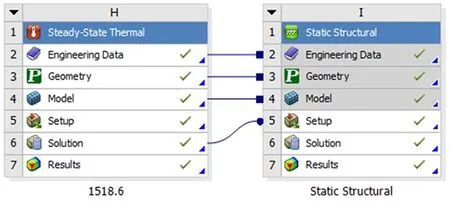
图7 轴承耦合分析步骤Fig.7 Step diagramof bearingcouplinganalysis

图8所示为齿轮箱单元高速轴轴承在稳定工作时轴承径向的热应变图。图9所示为齿轮箱单元高速轴轴承在稳定工作时的总变形图。从图中可以看出：当高速轴轴承在正常情况下稳定工作时，径向的最大热应变为0.000 364 06 mm/mm。最小热应变为0.000 336 17 mm/mm。整体趋势为内圈滚道热应变最大，往外圈方向逐渐减小。轴承的最大变形量为10.6μm，发生在轴承内圈端面上。由此分析可得，该轴承在正常工作时，应多注意轴承内圈和滚动体的散热情况。

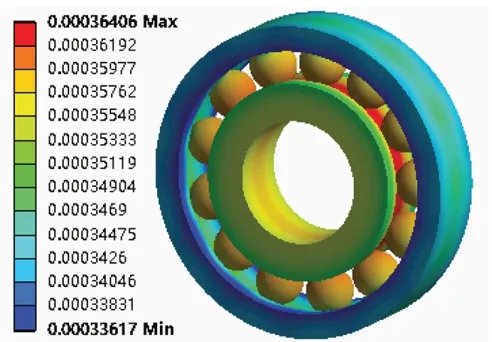
图8 轴承热应变图Fig.8 Bearingthermal strain diagram

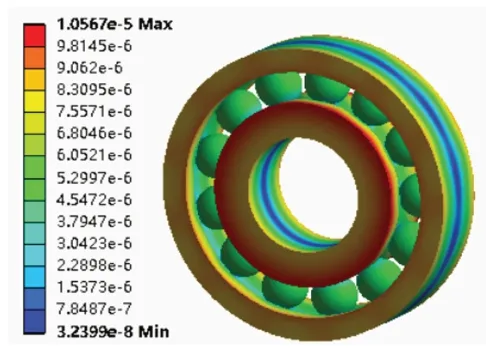
图9 轴承总变形图Fig.9 Total deformationof thebearing

4 不同因素对仿真结果的影响

轴承的温度场分布和热变形情况受到多种因素的共同作用。其中比较重要的因素包括轴承的径向载荷、轴承的转速以及环境温度。由于该海工平台齿轮箱单元高速轴轴承在工作时所受到的载荷远远小于该轴承的额定载荷，轴承径向载荷对温度场的影响比较小，所以在此，仅考虑轴承在工作条件附近的不同转速和不同环境温度下对其的稳态温度场和热-结构耦合场的影响。

4.1 转速对稳态温度场及热-结构耦合分析的影响

表5所示为高速轴轴承在不同的转速下的总摩擦力矩和生热量，此时环境温度选取为22℃，轴承的径向载荷为820 N。

表5 不同工况下轴承发热量Tab.5 Bearingheat generation under different workingconditions

当高速轴轴承在不同的转速下工作时，轴承温度情况如图10所示。由图中可以看出：随着轴承转速的不断提高，轴承温度均匀显著的上升，轴承中的最高温度和最低温度差也逐渐增大。

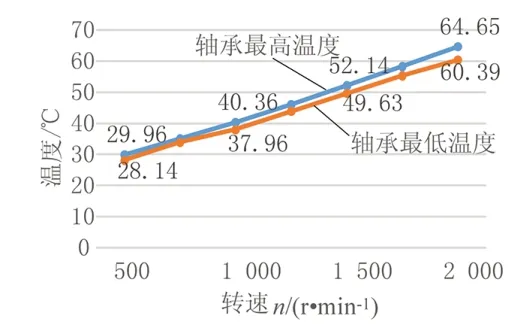
图10 轴承稳态温度随转速的变化曲线Fig.10 The curve of steady state temperature of bearing with speed

当高速轴轴承在不同的转速下工作时，轴承的总变形量和热应变如图11～12所示。从图中可以看出：轴承的总变形量和热应变随转速的增大而不断升高。最大热应变和最小热应变之差也不断增大。

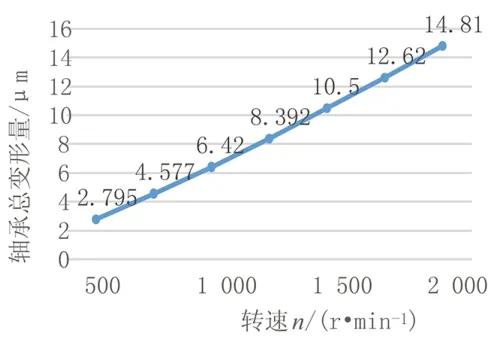
图11 轴承总变形量随转速的变化曲线Fig.11 The curve of the total defor⁃mation of the bearing with the speed

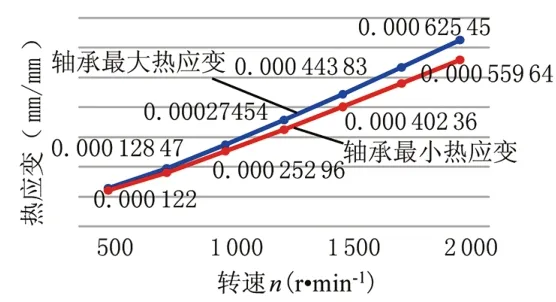
图12 轴承热应变随转速的变化曲线Fig.12 The curve of bearing thermal strain versusspeed

4.2 环境温度对稳态温度场及热-结构耦合分析的影响

当转速n=1 518.6 r/min，径向载荷为820 N时，轴承在不同环境温度下的稳态温度场如图13所示。轴承的整体温度随环境温度的改变而改变，整体趋势为线性增加，但环境温度的改变并不影响轴承内部温差。

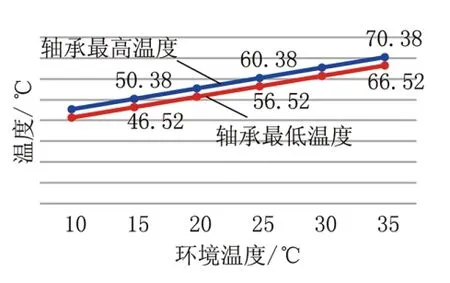
图13 轴承稳态温度随环境温度的变化曲线Fig.13 The curve of steady-state bearing temperature versus ambient temperature

不同环境温度下的轴承的总变形量和热应变情况如图14～15所示。轴承的总变形量随着环境温度的增加而不断增大，轴承的热变形量也随着环境温度的增加而不断增大，但整体趋势呈线性增长。

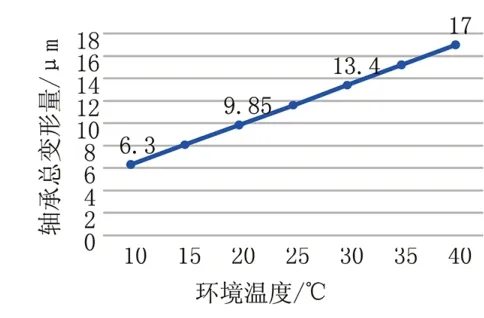
图14 轴承总变形量随环境温度的变化曲线Fig.14 The curve of the total defor⁃mation of the bearing with theambient temperature

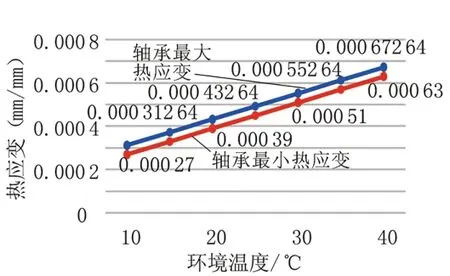
图15 轴承热应变随环境温度的变化曲线Fig.15 The curve of bearing ther⁃mal strain versus ambient temperature

5 齿轮箱单元高速轴轴承温度监测实验

为了准确测量齿轮箱单元平行齿轮箱工作时高速轴轴承附近的温度情况。在平行齿轮箱轴承附近箱体上开设探头式光纤光栅温度传感器安装孔，将标定好的光纤光栅温度传感器通过螺纹固定在安装孔中。传感器通过光纤跳线与解调仪连接，解调仪通过网线与上位机连接。现场试验安装如图16所示。

图16 高速轴轴承工作温度数据记录Fig.16 High-speed shaft bearing oper⁃ating temperature data record chart

图17 所示为高速轴轴承附近不同测点的实测温度。从图中可以看出，当轴承稳定工作时，高速轴轴承测点1的稳定工作温度为38.4℃，测点2的稳定工作温度为39.3℃。

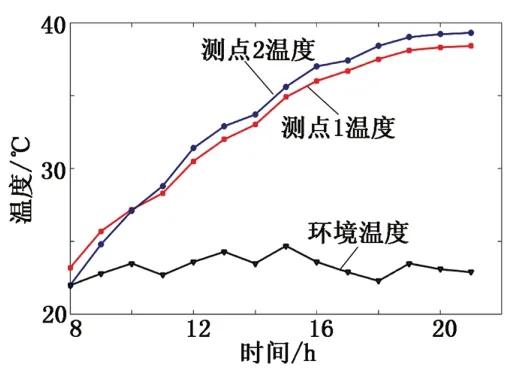
图17 高速轴轴承工作温度Fig.17 High-speed shaft bear⁃ing operating temperature

本文仿真与实验结果对比如表6所示。表中可以发现，控制初始环境温度和转速对应相等的情况下，在齿轮箱稳定工作时仿真结果与实验结果基本保持一致，验证了仿真过程和结果的正确性。

表6 仿真温度与实测温升的对比Tab.6 Comparison of simulated temperatureand measured temperature

6 结束语

本文具体以海工自升式平台升降系统齿轮箱高速轴轴承为研究对象，在经验公式和理论分析的基础上，确定了齿轮箱高速轴轴承的首要生热因素和传热情况。据此为边界条件，通过有限元建模仿真对轴承进行稳态温度场进行分析并加以实验对照，得出以下结论。

（1）海工平台齿轮箱单元高速轴轴承工作时，其稳态温度场分布情况为轴承内圈温度最高，滚动体其次，轴承外圈温度最低。其径向热应变最大点为内圈滚道，滚动体其次，外圈径向热应变最小。但轴承总变形最大点发生在滚动体上。

（2）海工平台齿轮箱高速轴轴承工作时，轴承温度随着转速的增高以及环境温度的升高不断增大，但轴承内部温差只随着转速的增高逐渐增大，不随着环境温度的升高而增大。

（3）海工平台齿轮箱高速轴轴承工作时，轴承的热应变和总变形量随着转速的增加以及环境温度的升高而不断增高。但轴承内部热应变之差只随着转速的增高而增大，并不随着环境温度的升高而改变。

本文以海工自升式平台升降系统作为研究对象，通过有限元仿真的方式对其高速轴轴承进行稳态温度场分析以及热-结构耦合分析，以期为海工装备轴承的设计、寿命研究提供有效参考和助力。海工工况复杂，技术发展缓慢，还需极大的努力和不断探索。