基于田口法的永磁同步电机单磁回路结构优化

林 帅，宋正东，占冬至

（上海新力动力设备研究所，上海 201108）

0 引言

永磁同步电机在工业场景应用中愈发广泛，涵盖了汽车、制造、航空和医疗等领域，具有小尺寸、大功率密度的优点[1]。小型工业用永磁同步电机一般涵盖交流永磁同步电机和无刷直流电机，而两者内部结构一致，因此旋转磁场基本一致。在电机转速提高到一定值时，输出转矩脉动将会变得显著，给电机带来振动和噪声，大大降低了电机的使用寿命和转矩精度。由于永磁同步电机的转子磁场由永磁所决定的，且永磁体磁场受永磁体结构限制，因此转子磁场由永磁体结构决定。而定子磁场为三相电流励磁磁场，励磁磁场不仅受电机定子结构影响，且受电流内谐波含量的影响，两者皆能导致转矩脉动的出现。由于定子结构的复杂性，电磁转矩往往伴随着齿槽转矩。在优化设计永磁同步电机过程中，需要对齿槽转矩的含量进行优化，来保证电磁转矩的平稳性。常用优化永磁电机都是通过优化其定子铁心的槽型参数，来改良定子中的磁场密度，或者通过优化转子中永磁体的安装方式和永磁体本身的结构进行优化磁场。本文通过一个对极下单磁回路中，环气隙定转子结构优化来对电机的转矩进行优化，由于电机结构具有对称性，磁场在旋转时每对极下主磁路所通过的路径一致，优化时可以大大提高效率。

本文采用田口法正交化实验的方法对磁回路结构参数进行优化。本文优化的永磁电机模型为内置式永磁体模型，主磁路回路中最容易导致磁场畸变的定子槽口结构和永磁体结构式影响电机性能的重要因素。本文以定子槽宽、定子槽齿齿桥根厚、槽齿半径和永磁体极弧系数为优化参数，以降低转矩脉动和齿槽转矩为优化目标，且保证电机输出扭矩满足额定转速时输出扭矩。最终通过正交实验后的参数表进行Ansoft Maxwell中二维有限元电磁场仿真，得到转矩值和空载齿槽转矩值，最终通过分析各参数对优化目标的影响程度分析来得到最优参数组，完成优化。

1 永磁电机定转子参数

本文所优化的永磁同步电机为4对极9槽内置式瓦片型永磁体转子磁路结构，该永磁同步电机在IPMSM结构优化设计中的应用，所设计的内置式永磁同步电机的有限元模型如图1所示。图2所示为其单极磁回路主磁路展开图。主磁路中的磁密分布直接影响电机输出的电磁转矩的性能，而主磁路模型中的定子槽齿结构和永磁体结构直接影响了磁路中磁密分布。基于此，对单极磁回路中的槽齿结构和永磁体结构进行优化实验。

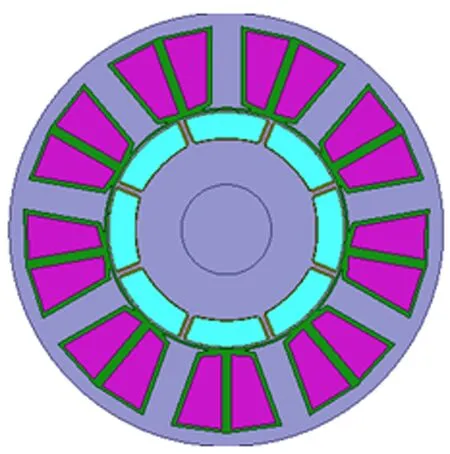
图1 9槽4对极永磁同步电机优化有限元模型

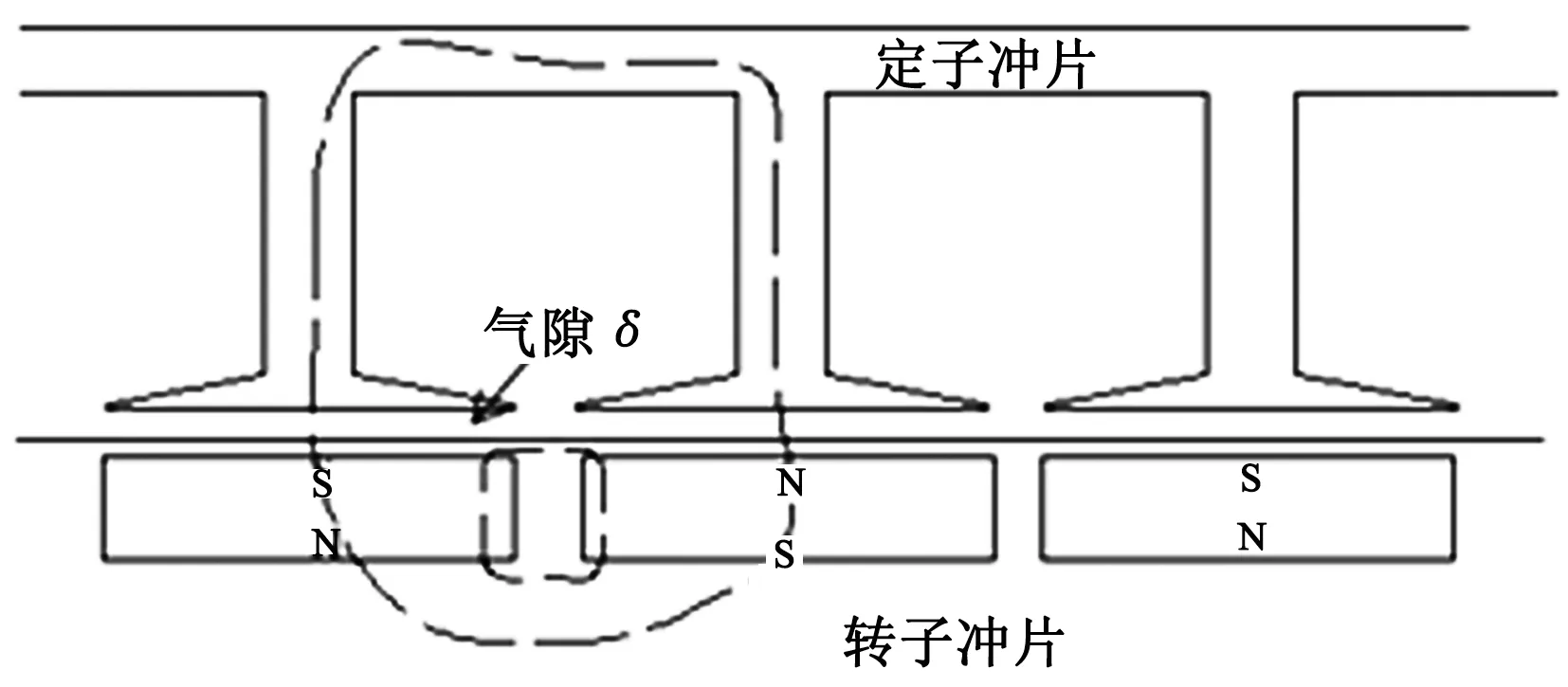
图2 单极磁回路展开图

在选取电机结构优化参数时，选取对电机输出转矩影响较大的几个关键参数，通过前期有限元处理分析，定子开槽槽口宽度对于磁回路中磁密饱和程度影响较大；齿桥根部厚度和齿冠半径影响磁路中有效磁通和磁回路磁漏情况；永磁体极弧半径直接影响电机反电动势波形。这些参数对电机的电磁转矩波动有着直接的影响，因此对这4个参数进行优化分析。电机原模型参数如表1所示。

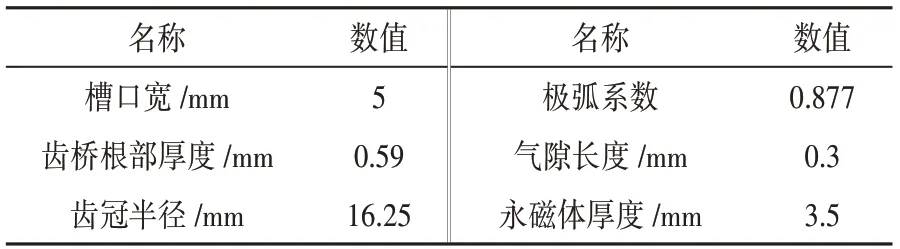
表1 原模型定转子主要参数

2 基于田口法的电机主要参数优化

2.1 田口法应用

在一个样机，多个优化参数影响其性能的优化实验下，需要大量的实验数据支撑。永磁电机具有复杂的磁回路因素，一般的优化算法对于其结构参数的优化组选取较为困难，且结果精确度不能保证，因此本文引入田口法。

田口法相较于其他优化算法，不涉及大量算法推导且模型运算要求低。不同模型设计不同的影响因子即可对不同的模型参数进行优化调整[2]。田口法通过3个步骤进行优化实验。图3所示为实验步骤的流程，通过流程可以得出，整个田口法实验所涉及的影响因子直接影响模型优化结果，因此在影响因子选择时，优化模型的数学模型为直接参考依据。由图得出以下步骤：（1）通过永磁同步电机的输出转矩数学模型，选取所要进行优化的目标参数，特定目标参数的选取涉及控制因子和干扰因子；（2）将控制因子和干扰因子梯度化分割，并做对应的田口直交表进行正交实验；（3）处理正交实验下的仿真结果值，分析其对优化指标所占比重，并得到最优参数组合解。

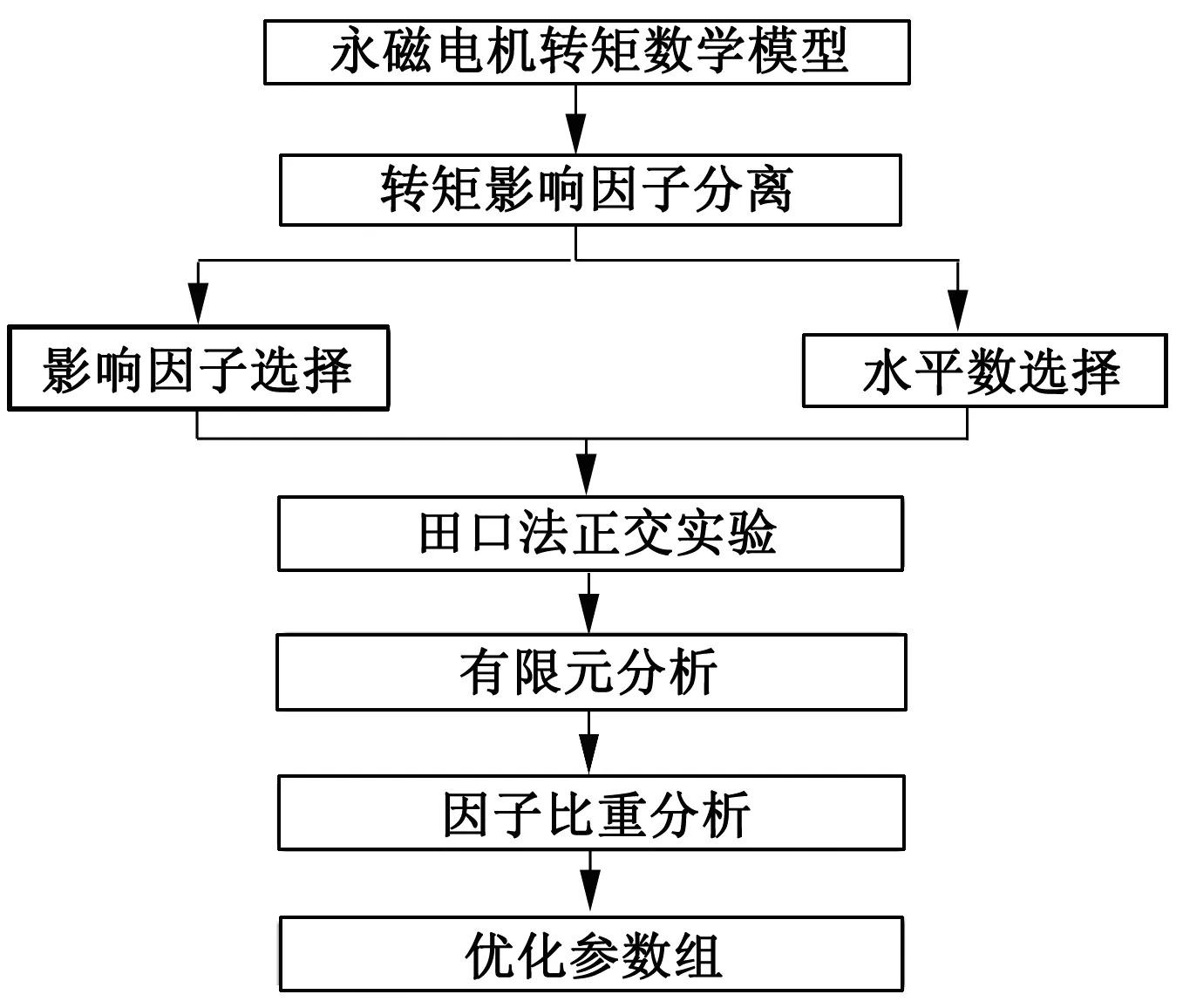
图3 正交实验步骤

电机电磁转矩在本体设计中所受最大的影响为定子槽所引起的齿槽转矩，根据能量法所得出齿槽转矩对于电机旋转角度的函数：

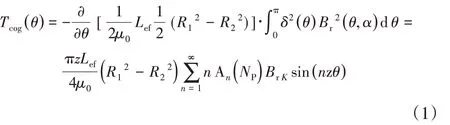
式中：R1为定子内半径；R2为转子轭外半径；Lef为电枢长度；当定子槽数与永磁体极数取最大公约数c时，z为定子槽数；BrK为定子槽数与磁极数公倍数时磁密傅里叶展开的K次系数。

从式（1）中可以看出：齿槽转矩脉动直接受定子铁芯结构影响，因此选择对定子结构包括槽口宽度、影响气隙磁导畸变的齿桥根部厚度、齿冠半径和永磁体极弧系数进行优化。

2.2 优化因子选取

优化参数的水平因子一般取3～5个值，各参数的每个值按照从小到大的顺序分别取名水平1、2、3等。本次实验对永磁电机的输出转矩进行优化，主要通过影响磁路的几个重要参数进行优化，每个参数取3个因子水平，图4所示为优化的4个优化参数对应的结构。

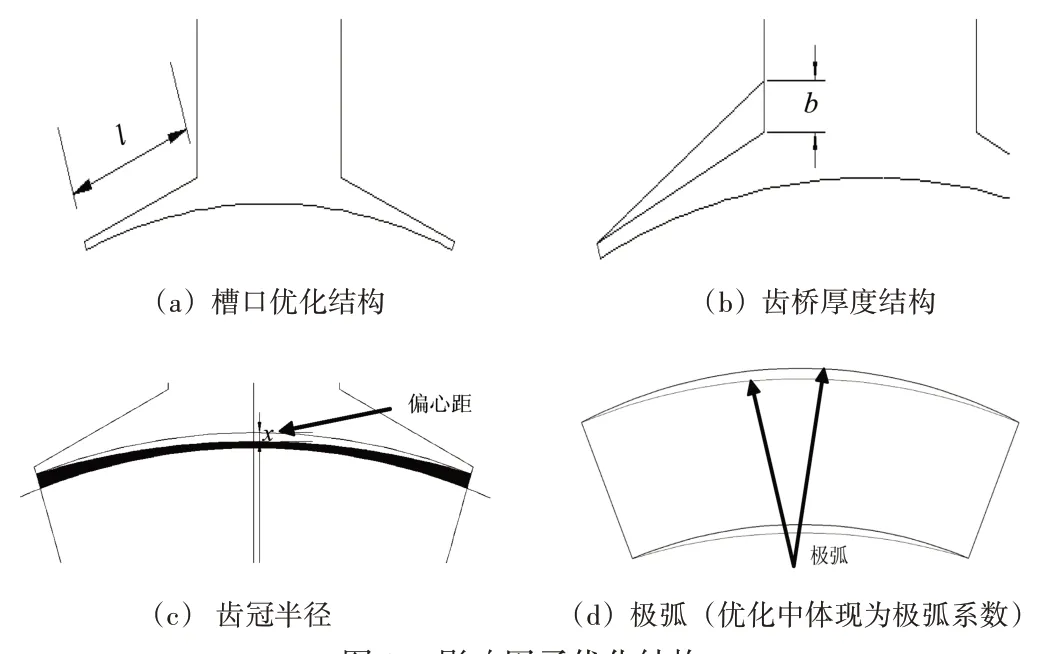
图4 影响因子优化结构

永磁同步电机优化参数及因子水平配置如表2所示，这些优化参数各水平的取值范围符合实际可加工要求。

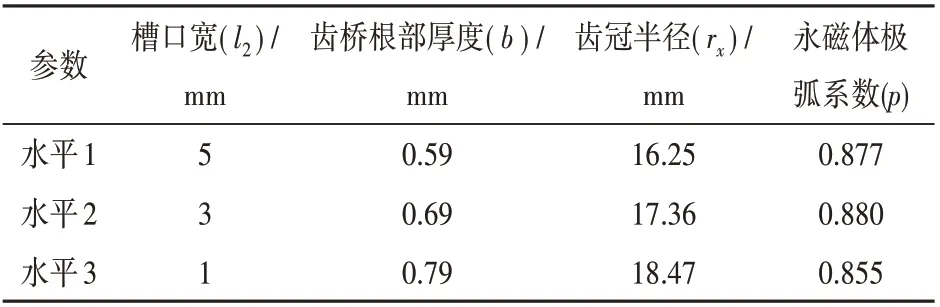
表2 永磁电机优化参数及因子水平配置表

表中影响因子直接影响磁路的磁饱和程度、漏磁系数和气隙磁密。

2.3 田口法正交实验

根据所选取的优化参数个数及其取值的水平数，建立实验正交表。正交实验表由水平数和优化参数个数正交而成，即Ln由Kt组成，其中n表示正交实验总次数，K表示各参数的水平数，t表示优化参数的个数。田口法正交表的优点是在表内每个参数的不同水平在参数列中出现的次数相同[3]。因此，可以保证任意两列横向优化水平是均衡的。

本文选取了4个3水平优化因子，根据正交法，建立L9（34）正交表，其中9为实验次数，3为水平数，4为优化参数个数，表3所示为正交实验排表。

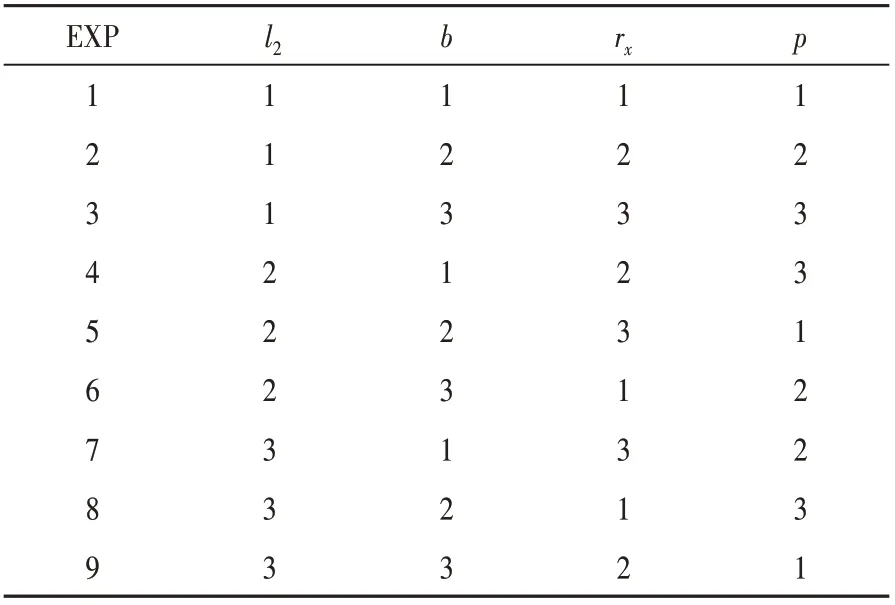
表3 L9（34）田口正交表

2.4 仿真结果及分析

通过正交表参数组合，对各组实验参数的结构模型进行有限元仿真分析实验。对各设计参数组合的永磁电机分别建模，得到其空载状态下的径向齿槽转矩，再在对应模型上面加额定电流负载，可得到额定电流下的电磁转矩，通过两者的值占比，可分析出定子结构的改变对其转矩的影响。

通过有限元仿真得到的实验结果如表4所示，其中包含电磁转矩Te、齿槽转矩Tcog和齿槽转矩占电磁转矩的占比kt。根据表中所得到的仿真值采用均值分析法对得到各个控制因子不同水准值对永磁电机的转矩波动的平均影响。

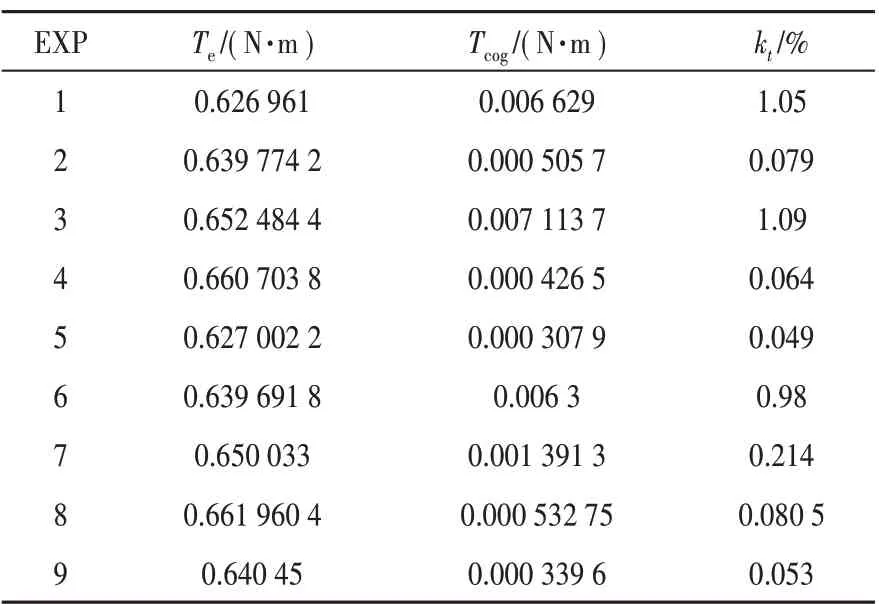
表4 正交表参数组有限元计算实验结果

平均值分析需要计算各变量在不同水平下电机仿真结果的平均值[4]。如电机转矩在永磁体极弧系数为水平1时的平均值计算如下：

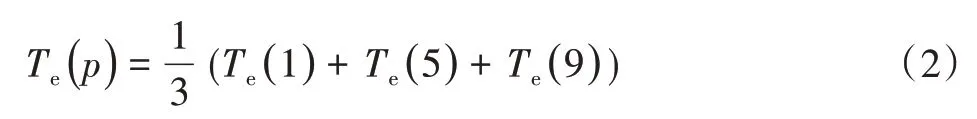
式中：Te(p)为永磁体极弧系数早水平1的转矩值；Te(1)、Te(5)、Te(9)为在第i次仿真实验时的结果，i=1、5、9。

根据该平均值计算方法，可以得到不同影响因子在不同水平下的平均值，结果值如表5所示。

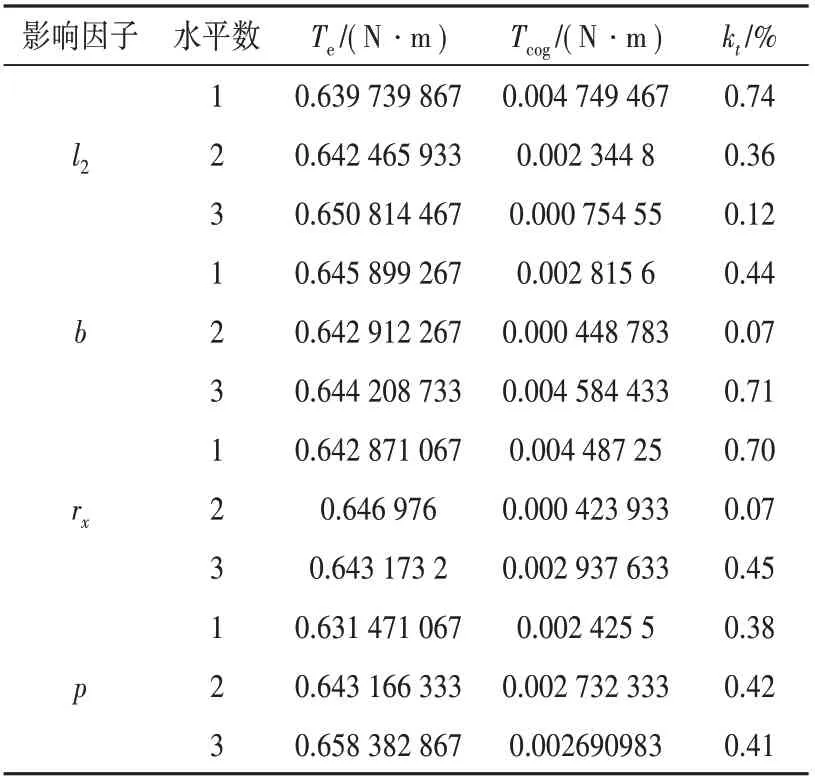
表5 因子平均计算值

计算完的平均值不能直观地看出各因子对于电机转矩性能的影响因素，因此可以利用方差值来表征其影响程度[5-8]，即：

式中：Sf为影响因子f的不同性能方差值；yi为不同因子在i水平下的实验结果；y为不同性能的平均值。

方差结果如表6所示。

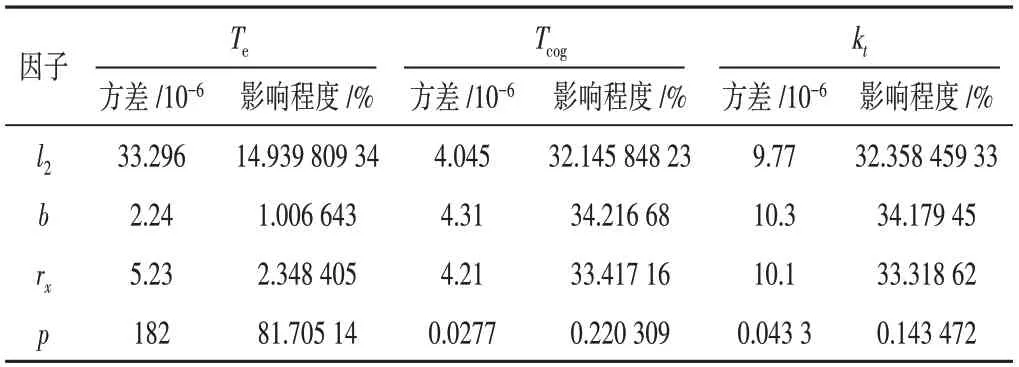
表6 优化因子方差值及影响程度

3 实验优选结果分析

3.1 最优参数组

各个优化因子方差值体现了不同因子在不同电机转矩性能下的影响程度，同时也体现了在4个影响因子中影响程度的占比。根据方差结果所得，电磁转矩受永磁体极弧系数影响较大，为了保证电机额定转矩性能，组合l2(1)，b(3)，rx(3)，p(3)；l2(2)，b(1)，rx(2)，p(3)；l2(3)，b(1)，rx(3)，p(2)；l2(3)，b(2)，rx(1)，p(3)；l2(3)，b(3)，rx(2)，p(1)的电磁转矩都满足额定转矩0.64 N·m的要求。同时，齿槽转矩的占比量较低的组合为l2(2)，b(1)，rx(2)，p(3)和l2(3)，b(3)，rx(2)，p(1)。

电磁转矩满足要求的前提下，本文优先选择齿槽转矩占比较低的组合，因此最终可以确定优化因子参数组合为l2(3)，b(3)，rx(2)，p(1)，其各参数值如表7所示。

表7 最优参数组

3.2 优化后电机转矩性能

通过最终得到的优化参数组在转矩有限元仿真计算后，由图5所示的齿槽转矩的波动图可以得出，经过优化后齿槽转矩大幅度地下降。

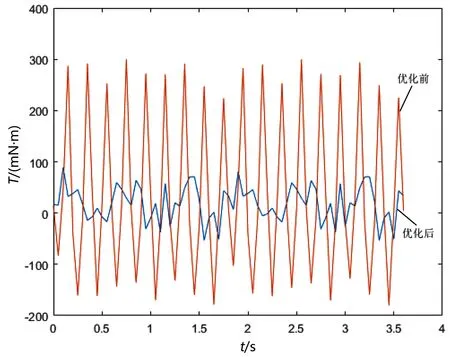
图5 齿槽转矩波动优化对比

根据表8中优化前后参数可以得出，齿槽转矩占比从0.375降至0.11，电磁转矩波动量从3.33%降至2.44%，转矩性能得到了极大地优化。因此从优化参数选择可以看出，单磁回路的结构参数对电机转矩波动具有敏感性。

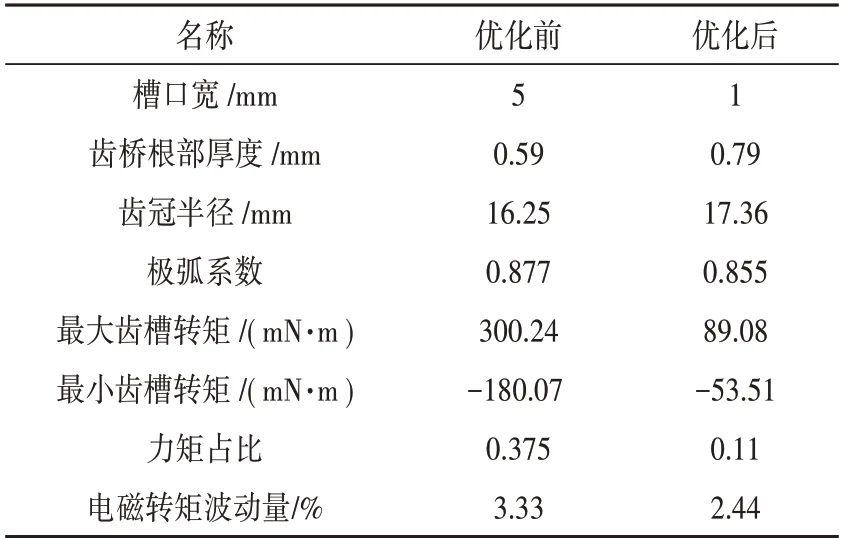
表8 结构优化数据

4 结束语

本文通过有限元仿真分析法和田口正交实验法对一台4对极9槽的内置式永磁同步电机进行转矩波动的优化。永磁同步电机的原始设计参数由电机力矩性能设计指标确定，由于有限元仿真计算得到的最初计算模型不具有最佳运行性能，因此根据能量法电机转矩的数学模型分析，找到影响转矩波动的参数因子组合。再利用田口法正交实验和有限仿真联合实验，找出最佳性能参数组，得到转矩波动最小的性能。通过对结果分析可以得到在一对极下单磁回路中，影响转矩波动的因素有定子槽端结构影响程度相当，而永磁体极弧系数对电磁转矩的影响最大。另外，利用田口法得到的正交实验组优选出转矩波动最小的优化参数组合，使得齿槽转矩下降70.6%，电磁转矩波动量下降26.7%，有效地通过田口法和有限元计算将转矩波动大的转矩结构参数优化，降低了波动率，且提高了整个优化周期，对实际电机单极磁路结构优化工程提供一种方法。