伺服系统中SVPWM过调制技术的发展与现状

罗金凤，王兴波，张 军，鄢继红

（1.佛山科学技术学院机电工程系，广东佛山 528000；2.广州数控设备有限公司，广州 510530）

0 引言

伺服控制系统是一个复杂的高性能调速系统，在实现从模拟信号到数字信号控制的过程中，脉宽调制技术（PWM，Pulse Width Modulation）是不可缺少的手段[1]。早期的PWM技术是采用自然采样法或规则采样法，但是计算上需要运用到复杂的超越方程，不利于工程应用[2]。后来出现了正弦脉宽调制技术（Sinusoidal PWM，SPWM）、空间矢量脉宽调制技术（Space Vector PWM，SVPWM），后者相较于前者具有更高的母线电压利用率、更低的开关谐波含量且更易于数字化实现，已逐步取代SPWM成为电机控制领域主流的调制手段[3]。

在SVPWM调制模式下，逆变器能够输出的最大不失真圆形旋转电压矢量为正六边形的内切圆，其幅值为即逆变器输出的不失真最大正弦相电压幅值为而若采用三相SPWM调制，逆变器能输出的不失真最大正弦相电压幅值为Udc∕2。显然SVPWM调制模式下对直流侧电压利用率更高，它们的直流利用率之比为1.154 7，即SVPWM算法比SPWM算法的直流电压利用率提高了15.47%。

SVPWM线性调制区的应用在21世纪90年代就已经十分完善，研究此类的学者发表了一些文章[4-13]验证了SVPWM技术的可行性，工业上开始了SPWM到SVPWM技术的过渡应用。其中，李涛[4]、熊健[5]作了SVPWM技术与SPWM技术的比较与优化，运用了三次谐波注入法，同时提出并验证了七段式代替五段式可降低33%的开关损耗。张成[6]、陆海峰[7]在规则采样法的基础上求得SVPWM调制函数在线性调制区的解析表达式，同时使用Matlab中的Simulink进行仿真验证与谐波分析，其中刘雪琴[8]同样作了仿真，但仿真模块不明确，很多参数被掩藏。相比之下，许军[9]的仿真更加成熟，详实，还加上了调节器对电机控制的模块，容易复现。徐善智[10]将SVPWM形成空间六边形的6个扇区的算法计算都列出来，十分详细。严洁[11]、王妍[12]直接运用数字信号处理（DSP）技术将其实时转换成算法运用到实际工程中。严海龙[13]针对在SVPWM算法中容易出现的疑问（实际是幅值等效法与功率等效法的系数有所不同）进行分类，将几种方法进行比较与统一。许文斌[14]主要验证了SVPWM技术在三电平逆变器中的应用，这是SVPWM技术可拓展的一个较新的研究方向，只是多电平逆变器的控制极为复杂，运用的逆变器数量多，损耗也相对增多。J Holtz[15]评价了三相电压源逆变器供电交流驱动器脉宽调制的研究进展，介绍了具有工业应用价值的前馈和反馈脉宽调制方案，并说明了它们各自的优缺点，另外还讨论了同步脉宽调制方案中负载电流相关的开关延时和瞬态等二次干扰，并提出了适当的补偿方法。昝健洲[16]、肖义[17]是在SVPWM已经运用完善的基础上对目标电机进行控制，提高电机精度及数字化控制。

综合以上文献，可完全细致地了解到PWM技术到SVPWM技术的基础原理研究与应用的过程，在电气工程不同的领域，不同的电机，不同的控制系统中，PWM控制技术都是必不可少的关键环节，所以目前对于在电机领域研究的学者，学习SVPWM技术是必须的。而重点研究SVPWM调制技术，则需要进一步的深入，即所研究的SVPWM过调制技术，本文将重点介绍SVPWM传统过调制技术研究以及最新的过调制技术的应用。

1 传统SVPWM过调制技术研究

在20世纪90年代之前，对于SVPWM技术的研究基本集中在线性调制区。随着电力电子技术中IGBT元器件的出现，相较于使用GTO的三相电压型逆变器，开关损耗大大降低，电机的驱动系统对输出的电磁转矩和逆变器的过载能力有所提高，由此SVPWM技术由线性可调制范围开始向过调制区域扩展。现在对于过调制技术的研究逐渐增多，而从调整策略上看，可以将全部过调制方法分成两类，一种是德国学者Holtz[18]于1993年提出的将整个过调制区域分为两个阶段，在两个阶段采取不同的参考电压调整手段的双模式过调制，另一种是意大利学者Bolognani[19]于1997年提出的在整个过调制区域只采用一种参考电压调整手段的单模式过调制。关于这两种模式详细介绍如下。

1.1 双模式过调制

德国学者Holtz提出将整个过调制区域分为过调制I区和过调制II区，为了最大程度地减少输出电压谐波含量，在过调制I区只调整参考电压矢量的幅值而不改变参考电压矢量的相位，而在过调制II区不调整参考电压矢量的相位将无法获得更大的基波电压，因此在过调制II区参考电压矢量的相位和幅值都将得到调整。通过面积等效原理可以计算得到参考电压矢量对应的控制角和保持角从而实现过调制I区和过调制II区的算法。

在双模式过调制中，定义过调制系数如下：

过调制Ⅰ区（不改变参考电压的相位，只改变幅值，调制系数范围为0.907≤M≤0.952）。在过调制Ⅰ区内，只改变参考空间矢量幅值的大小，而旋转角度没有任何变化。其复平面的6个扇区之一如图1所示。

图1 过调制范围Ⅰ区参考矢量电压的旋转轨迹Fig.1 Rotation trajectory of reference vectorvoltage in regionⅠof overmodulation range

图中虚线圆为所需的参考轨迹u∗。实线u∗p是由预处理器生成的轨迹，可以观察逆变器固有的物理约束，当参考轨迹在六边形内，旋转到长度为A-B的扇区的外角附近时，逆变器的控制可选择相邻的基本空间矢量以及零矢量按照正弦调制计算开启时间。然而，当原始参考轨迹通过六边形外时，相邻的基本空间矢量被最大化地利用，不再需要零矢量的参与，只有两个相邻的基本矢量被交替切换。在此过程中，平均电压轨迹沿与六边形重合的B-C方向移动。最后，轨迹到达点C，在另一个顶点附近。在这一区域中减少的基分量由A-B路径上更高的基分量补偿。计算B-C路径的开启时间可使用以下方程：

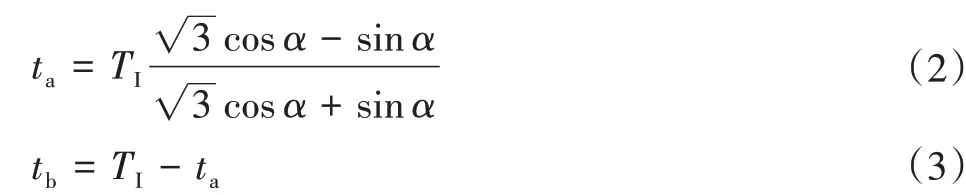
式中：ta与tb为参考矢量所在扇区的相邻基本矢量的作用时间；α为参考矢量的相角；TI为矢量旋转一个扇区的时间，TI=T0∕3。

为了在功能不那么强大的硬件上实现，可以通过一些权衡来简化第一个等式，如下所示：

只要参考轨迹的一部分存在于六边形内，就可以实现过调制范围Ⅰ区的脉宽控制。随着调制系数的逐渐增大，参考轨迹在圆形内的部分逐渐消失。修正后的轨迹与图中的六边形完全重合，六边形定义了在M=0.952时过调制模式Ⅰ的极限。

过调制Ⅱ区（参考电压矢量相位和幅值都需要改变，调制系数范围为0.952≤M≤1）。其中关键的参考矢量与实际矢量的变化过程如图2所示。

图2 过调制Ⅱ区范围内参考电压矢量变化Fig.2 Variation of referencevoltagevector in overmodulation regionⅡ

在过调制Ⅱ区的范围内定义参考矢量u*的角度为α，αh为虚线圆与六边形相交时的矢量相角。而六步阶梯模式的特征是保持一个特定的开关状态向量，这个开关状态向量在1∕6的基本周期内也就是α=π∕6时最接近参考向量。而参考矢量u*以基本角频率做圆周运动，在顶点处保持固定。其过调制范围的合成矢量是无法超过六边形的，所以参考矢量u*与实际矢量u∗p总是存在追踪的关系，参考矢量的相角变化如下：

1.2 单模式过调制

意大利学者Bolognani提出的单模式过调制算法在整个过调制区域内只采用一种调整策略，在整个过调制区域内参考电压矢量的相位都会有所调整，参考电压矢量的幅值保持不变，实现较双模式过调制算法更加简单。然而单模式过调制算法由于对相位的调整，输出电压谐波含量相比于双模式过调制算法要高，所以单模式过调制的研究工作相对较少。

在此单模式过调制中，过调制系数与双模式过调制相同。单模式过调制的参考矢量轨迹如图3所示。

图3 单模式过调制策略Fig.3 Single mode overmodulation strategy

为使逆变器平滑的进入六拍阶梯模式工作状态，设置矢量u→的行走轨迹为图3中实线，即如下所示：令时达到逆变器达到六步模式，其中αg=0，M=1。值得注意的是，在此调制模式上提出的方法中，幅值是不变的，因此避免了输出电压的突变，而且从扩大的意义上说，一个单一的算法管理了从过调制开始到六步模式，实现比较简单。

1.3 传统过调制技术的优化与发展

在以上SVPWM传统过调制技术中所定义的两种过调制只是这两种分类最初的一种调制方式，并不是唯一的。双模式过调制的分区思想更加深入人心是因为分区的方式会在提高直流母线电压的同时，最大程度上可降低电压输出的谐波含量，减小转矩脉动的问题，但是通过后期的研究会发现双模式中大多分区得到的过调制方式很难得到线性的结果，只能运用离线计算将数据存储到计算机中，在需要调制时再进行调用，这样就大大降低了精度，并且耗费存储空间，而后来对于双模式过调制的优化便是需要找到线性化的调制方式，减小计算量。单模式过调制的调制方式十分简单，可达到线性调制的结果，节省了存储空间，但有较大的问题是难以避免在整个过调制区域出现谐波含量高的情况，所以需要在这一方面进行优化。

随着传统过调制技术的研究与发展，许多学者在此技术上进行了诸多试验与优化[20-25]，Lee D C[20]应用双模式过调制的分区思想，将电压参考矢量角度和调制系数值之间的关系写在查找表中，为了实时实现，将过调制区域分段线性化，分析了输出电压的谐波分量和总谐波失真（THD），将该方法应用于感应电机的伺服控制系统中，实验结果表明，从线性控制范围过渡到六步控制模式时，电机可运行平稳。梁振鸿[21]对SVPWM计算得到的零矢量作用时间T0进行比较判断，同样是通过确定调制比，继而判断给定处于过调制I区和过调制II区，只是无需计算保持角度便能平滑地从线性调制区过渡到六阶梯波状态，减小了中间计算量。高莹[22]对限定轨迹双模式过调制算法作了详细的介绍，研究了各个有效矢量作用时间的计算方法，可以在线计算出各个参数，实现在整个调制范围内线性控制逆变器的输出电压，这种采用两个轨迹去计算参考矢量的方法是比较有潜力，运算简单，算法清晰。另外，不仅仅两电平逆变器可使用过调制技术来增高其转矩能力与电压利用率，多电平同样适用，比如李泽[23]也针对双模式过调制算法的分段处理思想应用到多电平逆变器的过调制算法中，效果也十分明显。

另外，对于单模式过调制算法，中科院电工所的张立伟等[24]提出了一种新颖的基于基波电压幅值线性输出控制的SVPWM过调制算法，该算法在整个过调制区域只采用一种调整策略且不需要存储大量的计算数据，能平滑地从线性调制过渡到六阶梯波模式，非常适合数字化应用，最后分析了该算法应用后逆变器输出电压的谐波畸变含量以及各次谐波的占比变化，谐波含量较传统单模式过调制算法有所改进。

2 最新过调制技术的应用

在上一章中主要是针对过调制理论上的算法进行有价值的汇总与介绍，而对于在电机上的实际应用则比仿真时的问题更加复杂，当驱动器在带动电机跑动时，会有动态和稳态两种情况，在不同状态下运用的过调制方案不同，也会直接导致电机的运行效果存在差异，所以目前对于这种情况，国内少有提及，而国外则针对此类问题展开了研究，接下来将对这些过调制方案进行介绍。

逆变器过调制在时态上看有两种过调制方式：稳态过调制方式和动态过调制方式。在考虑时态的这两种情况下，转矩能力依赖于用于过调制操作的过调制方案。通常，稳态过调制方案用于提供单位电压增益，达到逆变器的六阶梯波模式，也就是在双模式过调制中的理论运用。Y Park[25]和SK Sahoo[26]根据电压调制系数直接校正了参考电压，重点是在于指令电压的一个基本周期内实现单位电压增益，在转速或转矩指令的变化等瞬态过程中，不能快速处理超出逆变器电压限值的指令电压。因此，稳态过调制方案难以期望有良好的瞬态转矩响应。

与稳态过调制方案不同，传统的动态过调制方案，如最小相位误差、开关状态和最小距离误差过调制方案，可以简单地实现，并给出快速的瞬态转矩控制[27]。然而，由于过调制工作时的电压增益小于1，逆变器不能工作到六阶梯波模式。Seok J K[28]、B H Bae[29]、T Gemassmer[30]提出的过调制方案通过保持电流控制器给出的指令电压矢量的方向，改善了瞬态转矩响应。SLerdudomsak[31]通过计算新的指令电压来减小瞬态转矩的变化，从而增强了瞬态转矩响应。然而，这些过调制方案需要复杂的算法来实现，并且不能获得单位电压增益。为了使六步操作具有输出转矩的快速瞬态响应，Piao Chengzhu[32]提出了一种将改善瞬态响应的技术与稳态过调制方案相结合的方法。然而，由于存在一种额外的技术来改善瞬态响应，此方法使整个控制算法复杂化。Yun JH[33]提出了一种过调制方案，便于实现一种技术来改善瞬态响应。此外，JYoo[34]从几何角度分析了文献[35]中瞬态响应退化的原因，并提出了一种过调制方案来缓解这一问题。然而，由于这些方案不能用于稳态过调制方案，所以很难操作逆变器高达六步模式。

Jeong H I[36]区分了稳态时过调制与动态时过调制的工作模式，发现过调制对动态时电机的运行情况有比较大的影响，从而在直接数字脉宽调制法的基础上研究出一种三角交脉宽调制法，对系统的高动态系统有着明显的改善。

Jul Ki Seok[37]介绍了在动态过调制中3种经典的方法，即最小相位误差法、最小幅值误差法以及开关态。提出了一种简单的提高动态过调制电压增益的方法，将该方法应用于交流电机的弱磁控制中，可以最大限度地利用直流电压，有效地提高电机的输出转矩能力，并获得输出转矩的快速瞬态响应，且应用于连续脉宽调制和间断脉宽调制的动态过调制，并验证了该方法的有效性。以下简单介绍动态过调制中的3种经典方法，如图4所示。

图4 三种过调制算法Fig.4 Diagramof threeovermodulation algorithms

最小幅值误差法的基本思想为调整后参考电压矢量与原参考电压矢量的幅值差最小，从图4上看，调整后的参考电压矢量U1为原参考电压矢量Uref向极限六边形的边界作垂线后得到的矢量，当参考矢量过长时，由该点处向相应六边形边长所做的垂足超出本扇区，则实际输出电压矢量停留在最近的基本矢量上。最小相位误差法的基本思想为将超出可调制区域的参考电压矢量的相位保持不变，将其幅值减小到极限六边形的边界上，如图4中的U2，算法实现简单，在整个过调制区域都可实现。开关态的原理是矢量变换，将α-β坐标系转换成d-q坐标系[37]，这3种经典方法比较下来，开关态是最优的能使逆变器输出电压显著增加的方法，谐波含量小，且可以平滑地控制电机，在此算法上还有很大的延伸发展空间。

3 结束语

随着电力电子技术、自动化技术与计算机技术的发展，伺服控制系统在很多工业领域如数控机床与工业机器人应用中占据着极高的地位。未来伺服控制系统将全面发展为全数字化、智能化与网络化，而为数字化实现的SVPWM技术运用已经十分成熟且涉及多个控制领域中，紧接着对于SVPWM过调制技术的研究也在打开交流传动技术的局面上也非常占优势，而目前国内的电气传动技术与国外先进技术尚有一定差距，无论是理论研究还是技术应用中都存在着一些问题，还需要众多技术人员进行学习、研究与完善。本文针对伺服控制系统中的脉宽调制技术的发展以及SVPWM过调制技术的研究进行分类与整理，希望能给广大工程技术人员有价值的参考。