超声磨削加工表面分形维数计算方法★
冯 珂, 黄 卓
(1.山西工程职业学院, 山西 太原 030009;2.北方自动控制技术研究所, 山西 太原 030006)
引言
随着我国现代工业的迅速发展,各个重要场合如航空航天、高铁、汽车等领域的零部件需要具备传动效率高、承载能力强和使用寿命长等性能,这不仅对材料的力学属性性能提出更高的需求,同时也使得对先进制造技术的研究更显迫切。传统的加工方法,主要包括车削、铣削、磨削和抛光等对于传统材料的加工效果显著,但是对于新兴材料,如高温合金、硬脆性材料和复合材料等难加工材料则表现出粘刀、加工硬化、加工效率低、加工成本高、加工表面质量差等现象,这就迫切需要寻找新的加工方法来改善这些情况。因此,一些新的加工方法应运而生,例如超声振动辅助磨削。超声振动辅助磨削,也称超声磨削(UVAG)。该方法将超声波振动施加于砂轮上,磨粒受到超声波振动冲击而作周期运动。研究表明,超声磨削较传统加工方法细化了加工表面,降低了磨削力[1]和加工件的表面粗糙度[2-3]。
在传统的机械加工如车削、铣削加工方法中存在着分形特征[4]。看似复杂的图形经仔细研究发现,图形之间的整体或局部存在某种方式的相似性,这就是分形特征的体现,相对于传统表征方法具有不依赖于测量尺度和精度的优势,是物体本质属性的反映,这种避免尺度缺陷的表征方法可以更好地应用在微观形貌的特征研究之中。
维数的概念来源于对经典的欧氏几何的认识。在欧氏空间中,众所周知,人们通常用点、线、面、体来表示空间的维度。即用点表示零维空间,用直线表示一维空间,平面表示二维空间,立体表示三维空间且都为整数值。因此,当测定空间中的任意一个几何体面积与体积时,必须用与它相同维数的单位面积的正方形或单位体积的正方体去量度,则可得到一确定的数值。对于Koch 曲线,用传统的维数去测量(如一维和二维),结果发现Koch 曲线的维数为0或±∞。这说明Koch 曲线为非规则体,不能用整数维去测量它,这种非整数维就是分形维数。
Hausdorff 从测量的角度出发给出了Hausdorff维数定义,分形维数的定义由此产生[5]。对于n 维空间中的一个集合F,取边长为ε 图元对这个集合进行覆盖,统计出覆盖这个集合的总的图元的数目设为N(r),得到的D 就是Hausdorff 维数,它可以是整数或是分数。对于欧氏几何学中人类创造的简单理想标准体,可以知道他们的维数D 的值,D=0,1,2,3。但对于自然界的复杂真实物体,B.B.Mandelbrot 采用Hausdorff 维数来衡量这些极不规则的、维数有可能是分数特征的对象。经计算,二维曲线的维数在1~2 之间,而三维曲面的维数在2~3 之间。综上,本文基于盒维数法、差分盒维数法、结构函数法,用MATLAB 模拟出已知分形维数的理论分形曲面,对其进行分形维数的计算,并进行误差分析,从而确定超声磨削加工表面分形维数的计算方法。
1 分形维数计算方法
1.1 盒维数法
盒维数法是分析加工表面三维形貌分形特性最常用的方法[6],其优势的原因在于它的简便性和自动计算能力[7]。该方法是通过用不同盒子尺寸r 重复覆盖分形曲面,然后求出完全覆盖分形所需的盒子数N(r)。N(r)、r 和分形维数Ds的关系式表示如下:

对上述方程两边同时取对数,可得(2)表达式:

最后,如果r 尺度的值在适当的范围内,直线的斜率即为分形维数Ds的值。
1.2 差分盒维数法
在盒维数法基础上Sarkar N[8]等人提出了新的分形维数的有效计算方法—差分盒维数法(DBC)。其计算方法原理图如图1 所示。对于表面面积为M×M 的形貌采用大小为S×S 的正方形划分成若干个网格。S×S网格内,其中S 为整数且1 图1 差分盒维数算法原理图 这时尺度为r 的总盒子数N(r)在三维形貌的第(i,j)个网格内的分布nr(i,j)可表示为: 式中:nr(i,j)为第(i,j)个格子中的盒子数,则总盒子数为: 依次变换S 值,按照公式(3)和(4)计算得到对应的Nr值。再利用(2)式将lgNr和lg(1/r)进行最小二乘法拟合,直线的斜率即为分形维数Ds的值。 Blackmore D[11]采用结构函数法计算了已知维数的分形曲线。其定义是:假设R3表示三维空间,随机表面过程Z(x)可以用结构函数的方式表示为如下表达式: 假设分形曲面可由连续函数表示,则有S={[x,y,Φ(x,y)],Φ(x,y)、(x,y)∈R},其中,-a≤x≤a,-b≤y≤b,Φ(x,y)代表的是表面高度。 结构函数法计算分形维数的具体计算过程如下: 1)在表面的区域内,选取一随机点X0=(x0,y0),以此点作为基点,则该点的高度值可用Φ(X0)度量。将剩下的数据,在以X0为中心的极坐标下进行采样,采样公式如下: 2)令θ=2πi/m,i=0,1,2,3,…,m-1。径向距离rj=jr*/n,j=0,1,2,3,…,n,对于某些较小的实数r*<0。为了获得足够多的数据,m 与n 应该选取较大的合适正整数。 3)在此0≤i≤m-1,0≤j≤n 范围内,与前一个点间距相等的高度值可表示为如下表达式: 4)令Δij=|Zij-Z0|,则各个相等的间距点的高度与原点的高度之差的平均值表达式为: 5)依次改变径向距离rj的值,根据表达式(8)计算得到相对应的Δj的值。在双对数坐标中,作出(lgrj,lgΔj),并采用最小二乘法对数据点进行拟合,即可得到直线的斜率Lh,然后求得分形维数。分形维数Ds=3-Lh。 Weierstrass-Mandelbrot 函数简称W-M 函数,常用于分形曲面的重构。W-M 函数处处连续但是并不可微,且具有分形的自相似的特性。采用W-M 函数可以模拟出分形维数为Ds 的分形曲面的表示形式如式(9): 式(9)中:Cn是独立的且服从均值为0,方差为1 的正态分布随机数;An,Bn是独立的且都服从[0,2π]上的均匀分布的随机数;Ds为分形维数,且2<Ds<3;λ 为大于1 的常数;n 为自然序列数。 编写W-M 函数的matlab 程序,在matlabR2015b 中分别模拟出分形维数Ds=2.1、Ds=2.2、Ds=2.4、Ds=2.5、Ds=2.7、Ds=2.8 的理论分形曲面。下页图2 所示是由MATLAB 模拟出的分形维数为Ds=2.1、Ds=2.2、Ds=2.4、Ds=2.5、Ds=2.7、Ds=2.8 的分形曲面。由图可以看出,不同维数的分形曲面结构特征是不相同的,且随着分形维数逐渐变大,分形曲面的形貌变得较复杂,且形貌中的精细结构越明显。因此得出,分形维数与表面的整体形貌的精细、复杂程度呈正相关,从而可以全面表征整体形貌的特征。表明形貌较光滑时,分形维数就较小;表明形貌精细的结构越多,分形维数就会越大。当Ds<2.5 时,三维表面的复杂、精细结构随分形维数的增加而缓慢地增加,但是当Ds>2.5 时,三维表面的复杂、精细结构大幅变化,高频成分明显增多,表面结构具有较高的能量。 图2 Weierstrass-Mandelbrot 分形曲面 在第一节中,比较全面地呈现了盒维数法、差分盒维数法、结构函数法这3 种分形维数计算方法的计算流程及算法思想。为了找到最适合超声振动辅助磨削加工表面的三维分形维数计算方法,本文将对盒计数法、差分盒维数法、结构函数法进行优选。在matlabR2015b 中分别模拟出已知分形维数Ds=2.2、Ds=2.5、Ds=2.8 三个理论分形曲面,选择超声磨削实验加工表面的采样条件,然后利用这三种分形维数的计算方法,针对三个已知分形维数理论分形曲面计算出实际的分形维数,结果如表1 所示。 表1 模拟理论表面分形维数 将这3 种算法所得的计算值与理论值相比较,发现盒维数法的计算结果与理论的值最接近;差分盒维数法是在盒维数法基础上进行改进的算法,其计算结果相比较于盒维数法偏差较大;结构函数法的计算值离理论偏差最大。图3 为超声磨削加工扫描电镜下的表面灰度图像,超声磨削加工后的表面是由一系列的凹槽、划痕等精细结构所组成,而盒维数法的算法思想与之较一致。即盒维数法较适合计算超声磨削加工表面的分形维数,其精度高于差分盒维数法、结构函数法。综上,本文选择盒维数法来计算分形维数。 图3 超声磨削加工表面灰度图 1)本文根据W-M 函数编制理论分形曲面的MATLAB 程序解释了分形维数所表示的物理意义。分形维数Ds是度量复杂物体复杂性的一个定量指标,代表的是系统填充空间的能力。分形维数与表面的整体形貌的精细、复杂程度呈正相关。表面形貌较光滑时,分形维数就较小;表面形貌较粗糙时,表面形貌越精细,分形维数就越大。 2)通过MATLAB 模拟已知分形维数Ds=2.2、Ds=2.5、Ds=2.8 三个理论分形曲面。分别用盒维数法、差分盒维数法、结构函数法这三种方法计算模拟的已知分形维数的理论分形曲面并分析结果,结果表明:盒维数法计算精度较高,选用盒维数法计算超声振动磨削加工表面微观形貌。
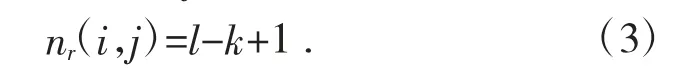

1.3 结构函数法




2 分形理论曲面及其算法分析
2.1 分形曲面MATLAB 模拟


2.2 超声振动辅助磨削加工表面的分形维数算法选择


3 结论

