基于精英保留遗传算法孔边疲劳裂纹扩展数据处理*

马成龙，张 晗，孟丽君

(江汉大学智能制造学院，湖北 武汉 430056)

0 引言

金属材料在交变应力或在应变作用下会发生疲劳[1]，疲劳损伤是机械损伤的最常见形式，占全部力学破坏的50%～90%[2]。机械装备一旦发生损伤破坏而导致结构断裂和故障，将带来重大的经济损失和严重的社会影响。因此，及时监测机械装备的裂纹损伤信息并对其剩余寿命进行预测，是保证设备安全运行的重要保障[3]。为此，需要测试材料的疲劳裂纹扩展速率，稳定裂纹扩展段的疲劳裂纹扩展速率常用Paris公式描述[4]，该公式是预测疲劳裂纹扩展寿命的经典公式，常用于长裂纹稳定扩展行为的研究。常见的疲劳裂纹扩展实验的数据处理方法有割线法和递增多项式等[5]。本文以2019 PHM Conference Data Challenge挑战赛公布的试件裂纹长度和疲劳循环次数的实验数据为基础[6]，通过python编程，利用遗传算法对施加了恒定载荷和变载荷的实验材料稳定阶段疲劳裂纹扩展的Paris公式中材料参数进行多目标优化求解，得到了较优的Paris公式参数和a-N曲线拟合结果，依据计算结果可以实现少数据点情况下材料疲劳裂纹的寿命预测。

1 Paris公式

如图1所示，材料的裂纹扩展速率和应力强度因子的关系可以划分为三个阶段[1-2]，分别为A、B和C三个阶段，在材料裂纹扩展的第一阶段A内，应力强度因子ΔK和裂纹扩展速率da/dN都相对较低。在阶段B内材料应力强度因子变程大于门槛值，为稳定裂纹扩展段，该区域内裂纹扩展速率da/dN与应力强度因子变程符合Paris公式，是目前研究的主要区域。在区域C，材料裂纹快速扩展，da/dN值很大，在实验研究中通常不考虑。

Paris公式是描述稳定扩展段的疲劳裂纹扩展速率公式，其方程如下：

da/dN=C(ΔK)m

(1)

其中，a是裂纹长度或深度，N是负载循环数；da是裂纹长度增量，dN是负载周期的增量，da/dN是裂纹扩展速率；ΔK是应力强度因子变程；C和m是材料参数。

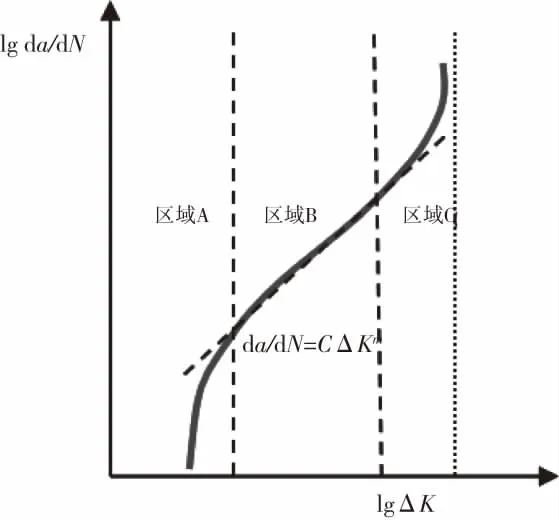
图1 裂纹扩展曲线

应力强度因子幅值ΔK可以表示为[1]：

(2)

其中，Y是试样的几何因子，对于孔边疲劳裂纹，其值为[6]：

Y=[1+0.2(1-s)+(1-s)6](2.243-2.64s+1.352s2-0.248s3)

(3)

其中，Δσ为施加的应力范围，取Δσ=4e7 Pa，s值为：

s=a/(R+a)

(4)

其中，R为孔边的半径。

本文中取R=4e-4 mm。

1.1 实验样品施加载荷

对于实验样品T1至T3，施加的疲劳载荷振幅谱是恒定的；而对于样本T4则是变化的。两种类型的载荷振幅图如图2。

由图2可以看出，在对实验样品施加恒定载荷谱的情况下，应力范围可以表示为：

Δσc=σmax-σmin=100.21-4.77=95.44 MPa

(5)

图2 疲劳载荷振幅谱

1.2 变载荷的等效应力幅

针对变载荷作用下裂纹扩展的高载迟滞和低载加速特征[7]，已有研究人员提出多种Paris 修正公式[8]，可对变幅载荷下的疲劳裂纹进行合理解释，但是一般的修正公式参数较多，拟合也较困难。对于变幅疲劳计算通常近似按线性疲劳累计损伤Corten-Dolan准则[9]，将变化的载荷幅折算为恒定幅。其表达式为：

(6)

其中，N是应力加载的总循环数；σl是最大应力水平值；Nl是最大交变应力作用下的总循环数；σi是第i级应力水平的应力值；ai是第i级应力的循环数占总循环数的比值；d是实验确定的常数。

对公式(1)进行积分，可以得到：

(7)

其中，a1，a2为裂纹初始长度和实验扩展阶段结束时的裂纹长度。将Δσ表示应力幅，则有：

(8)

令

(9)

则式(8)变换为：

N=β(Δσve)-m

(10)

将式(10)带入式(6)可得：

(11)

通过上述公式计算可以将变幅载荷作用下的疲劳裂纹扩展问题，引入等效应力Δσve来表示，以便后续进行计算。

1.3 常用的七点法求材料参数C和m

依据GB/T 6398—2000《金属材料疲劳裂纹扩展速率实验方法》[10]，将测得的a，N数据进行拟合求导处理，则Paris公式(1)在双对数坐标系中可变换为：

lg da/dN=lgC+mlgΔK

(12)

从式(12)中可以得到直线的斜率为m，直线在lg(da/dN)轴上的截距为lgC，最终求得Paris公式中的材料参数C和m。

但是这种方法在拟合的过程中将C和m看做定制，没有考虑材料本身、测量误差、环境等因素导致的C和m离散性[11]。研究表明，C和m的分布分别呈对数正态分布和正态分布[12]。

本文针对传统方法的局限性，提出了基于精英保留遗传算法进行材料的疲劳裂纹扩展规律预测。在整个过程C和m会在给定的边界条件中进行编码处理，使其不再被看成确定的值，服从一定的分布规律，符合实际条件。在算法中设定C的上下边界为[1e-10，1e-9]，m的上下边界为[2，4]。

2 数据处理

2.1 实验数据

对于实验样品施加疲劳载荷后得到数据T1、T2、T3和T4，见表1(数据来自：2019 PHM Conference Data Challenge)[13]，其中前三组数据为施加恒定载荷得到的数据，T4为施加变载荷得到的裂纹扩展数据。

表1 实验样本数据

2.2 精英保留遗传算法原理

精英保留遗传算法(Elitist Strategy Genetic Algorithm，简称ESGA)，将群体在进化过程中出现最好的个体不对其进行配对交叉等操作，直接复制到下一代，进而避免了一般遗传算法中杂交变异过程中较好基因被破坏的可能性。其流程图见图3。本文采用精英保留策略遗传算法对实验数据进行处理，通过Python的遗传算法工具箱geatpy，调用增强精英保留多染色体算法模板进行优化求解。

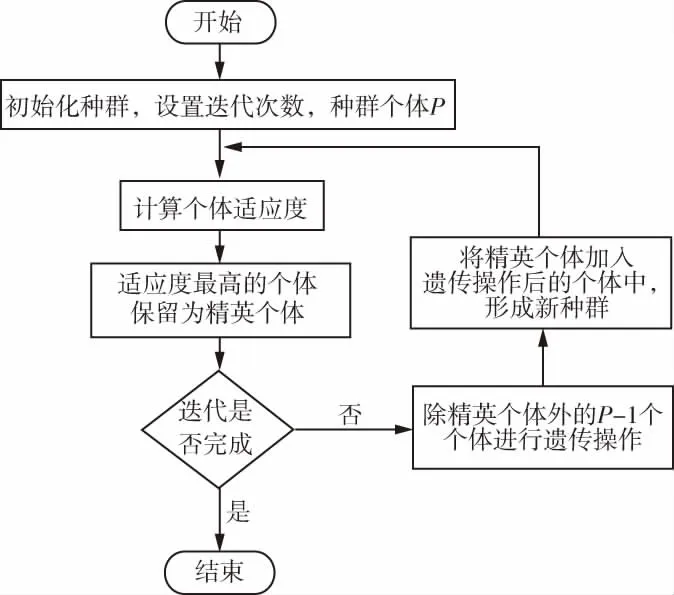
图3 精英保留遗传算法流程图

图4和图5分别是程序计算后材料参数C和m的最终值(虚线)和一代种群更新对比图，其中因得到的材料参数C的值较小，将其转化为对数分析。从图中可以看出，算法采用精英保留的策略，将搜索到适应度最高的个体作为精英个体在种群进化过程中得以很好的保留。

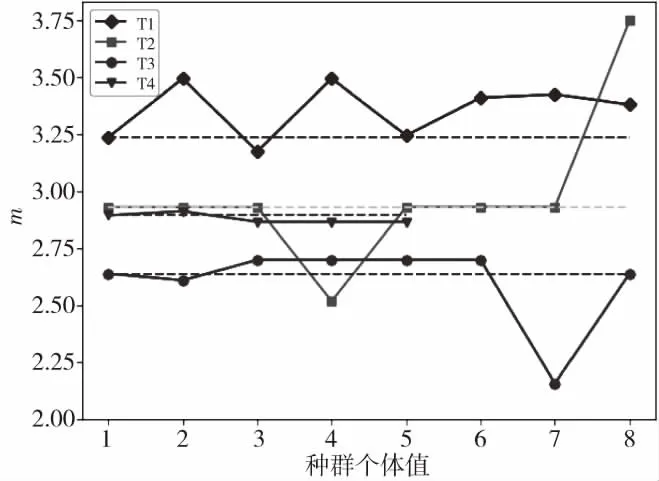
图4 程序优化得到的材料参数m

图5 程序优化得到的材料参数C的对数

2.3 疲劳裂纹扩展曲线

然后通过编程对实验数据进行处理分析，图6给出了计算程序流程图。

对于表1中各个实验样本数据，通过编制程序进行多项式最小二乘拟合得到样本的疲劳裂纹扩展曲线，恒定载荷样本结果如图7、图8和图9，变载荷样本实验数据结果如图10。

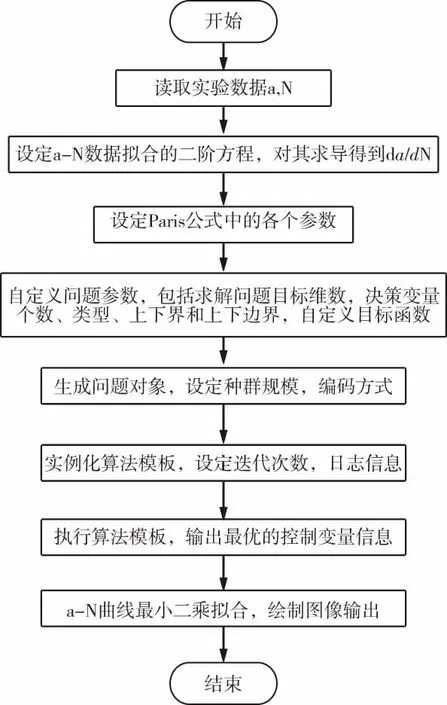
图6 Python计算程序框图

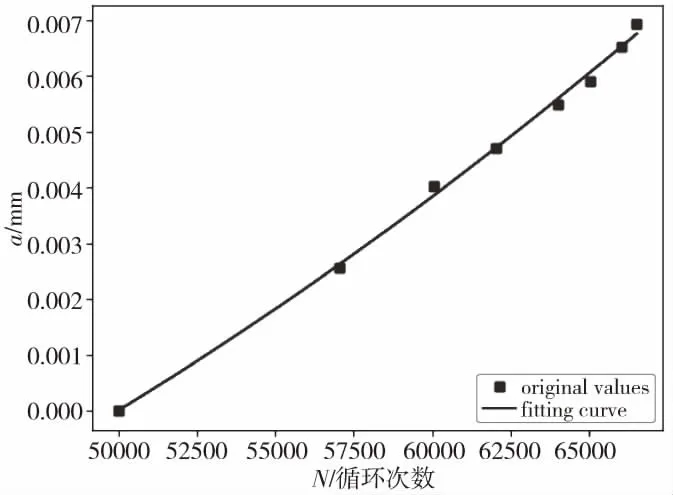
图7 T1疲劳裂纹扩展曲线

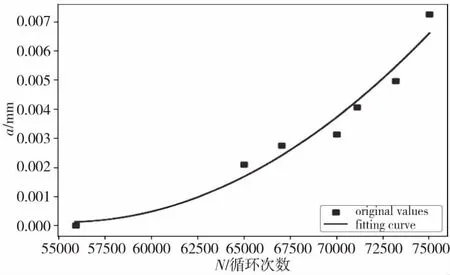
图8 T2疲劳裂纹扩展曲线

本文选择样本可决系数R2反映样本值拟合情况，表2为四组数据曲线拟合的可决系数值。由表2可看出，四组数据R2值均在0.9以上，拟合效果良好。

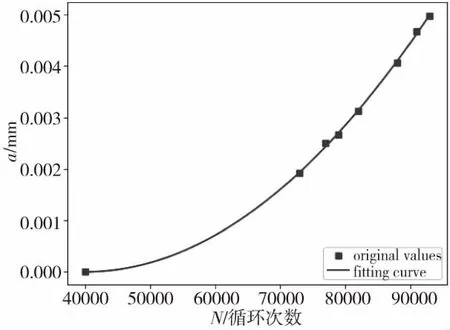
图9 T3 疲劳裂纹扩展曲线

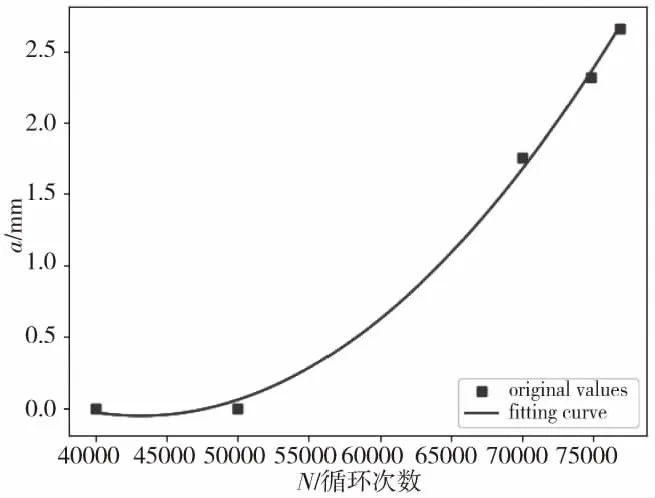
图10 T4 疲劳裂纹扩展曲线

表2 拟合可决系数

2.4 材料参数

通过Python编写的程序，采用精英保留的多染色体遗传算法，在导入实验数据迭代100次后得到的实验样本的材料参数如表3所示。

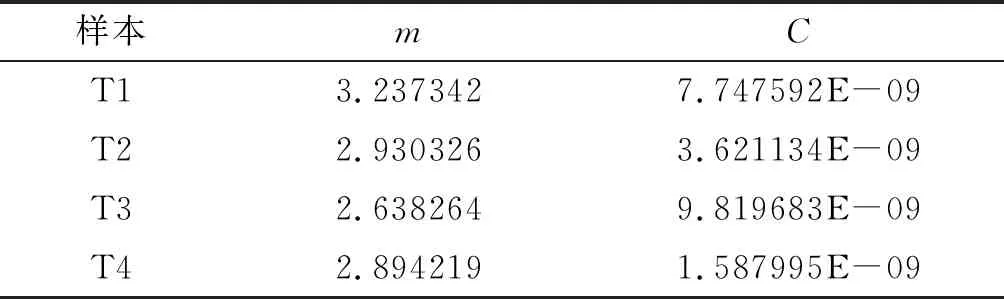
表3 实验样本C和m

对于实验样本T4，由于施加的载荷振幅是变化的，所以在对其进行求解时将其用等效应力Δσve来代替，在程序中设定为新的一个决策变量，并设定其上下界为[4e7，9e7]，最后计算得到其载荷循环的替代值为Δσve=4.0002249×107Pa。

下面对计算结果T1的材料参数进行验证。由文献[11-12]可知，若把C看成一个确定的值，则lgC也是确定的，这时m服从正态分布。图11为得到多次结果后m和lgC的关系图。拟合得到的参数方程为：

m=1.488lgC+15.839

(13)

取lgC的均值为-8.657928，则C值为2.198226e-9，依据方程(13)可求得m的值为2.958647。此时均值对应的Paris公式为：

da/dN=3.510750×10-9(ΔK)2.956003

(14)

图11 lgC和m关系图

上述过程将C看作是一个定值，通过文献[13]可知，这时m服从正态分布。由程序多次运行后得到500个m的值，作出其分布直方图如图12所示。从图中可以看出m近似服从正态分布。

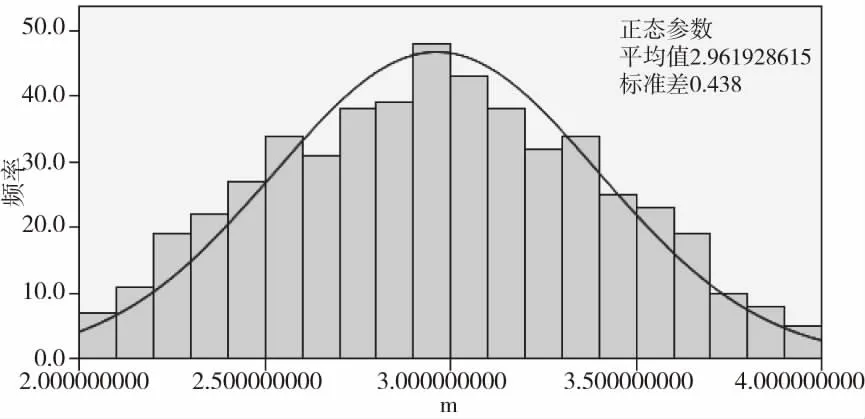
图12 m分布直方图

通过SPSS软件对m进行单样本柯尔莫戈洛夫-斯米诺夫(Kolmogorov-Smirnov，简称K-S)检验[14]，结果如表4所示。

由检验结果可知，渐进显著性水平为0.200，大于0.05(小概率事件的概率值)，所以m的分布特性为正态分布。m的均值为2.961929，此时对应的均值Paris公式为：

da/dN=3.510750×10-9(ΔK)2.961929

(15)

表4 单样本K-S检验

式(14)和式(15)对比差异非常小，说明通过精英保留遗传算法估计的材料参数较为良好。

3 总结

针对传统的使用Paris公式预测疲劳寿命问题，本文提出了基于遗传算法对实验数据进行分析处理，预测其疲劳裂纹扩展规律，得到其材料参数C和m。主要有以下结论：

1)基于精英保留策略的遗传算法，计算过程中将材料参数在边界条件中进行编码处理，由于材料参数本身的离散特性和实验数据数量的局限性，作为精英个体保留输出后的材料参数服从一定的分布，且会更加逼近实际值。

2)针对获得的少量数据点，在变载荷条件下算法仍能够得到较为精确的材料参数，且随着数据点的增加结果将更为精确。