拉曼-米激光雷达测温通道残余几何因子修正

陈思颖，年璇，陈和，张寅超，郭磐

（北京理工大学 光电学院， 光电成像技术与系统教育部重点实验室，北京 100081）

温度是描述大气状态的一个关键参数，在大气动力学、气候学和气象学等领域起着至关重要的作用[1]. 边界层温度受地面辐射的影响很大，且经常出现逆温层，变化十分复杂. 准确测量边界层内温度分布对于研究天气预报、大气变化和气候监测等具有十分重要的意义. 目前，除了现场测量（如无线探空仪）外，也有许多被证实可行的大气温度遥感技术，包括主动遥感技术（如激光雷达）和被动遥感技术（如微波辐射测量）等[2−3]. 由于激光雷达具有测量精度高、时空分辨率高和探测范围广的优势，因此被广泛应用于大气温度的研究. 转动拉曼激光雷达目前是对流层温度探测最可靠的技术之一[4−6]. 该技术利用纯转动拉曼谱线强度对温度的依赖关系，从激光雷达接收的两个具有不同温度敏感性的部分转动拉曼信号比值中反演得到温度廓线.

激光雷达的几何因子为各个高度处接收系统接收的回波信号与该高度处全部回波信号的比值[7]. 理想情况下，对于使用同一接收视场的两个通道，望远镜视场与出射激光束不完全重叠所造成的几何因子应该是一致的. 然而在实际应用中，两通道的几何因子受到各自通道内的光学器件和探测器的影响而存在一定的差异. 产生这种影响的原因可能是，望远镜接收到不同高度处的回波光信号聚焦到光阑上的光斑位置不同，经光纤传输和光栅分光后，高低阶信号聚焦的位置也就偏离了理想位置，造成高低阶信号不同高度上接收效率不同的问题，进而导致在拉曼信号比值中存在残余几何因子的影响[8−9]. 若未修正两通道的残余几何因子，势必会在近地面温度反演中引入较大误差.

目前，国内外学者已经提出了几种修正残余几何因子的方法，主要有系统改进和数据修正两种方法. 系统改进类方法的主要思路是通过在接收系统中加入光学器件，从而使得接收到的光学信号的横截面不随回波信号的高度而改变，可以通过在回波光路中加入一个光阑或使用光纤扰频器结合傅里叶变换透镜的方法来实现[10−11]. 数据修正类方法是通过将系统在实验中测得的比值信号与探空气球采集的温度数据相比较的方式标定得到残余几何因子廓线[12−13]. 数据修正方法无需对系统进行改动，应用方便，但现有的修正方法依赖温度反演精度，容易受到噪声的影响.

针对高低阶拉曼通道几何因子存在差异性的问题，提出一种简单的修正残余几何因子的方法. 该方法首先通过探空温度和标定的归一化光谱透过率计算出高低阶拉曼通道有效微分散射截面，然后由拉曼信号比值求解得到残余几何因子. 利用实验室自行研制的转动拉曼-米激光雷达系统的探测数据，对该方法的有效性进行实验验证.

1 基本原理

根据激光雷达方程，转动拉曼-米激光雷达中纯转动拉曼信号可以表示为

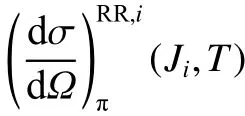
考虑两通道系统常数差异以及残余几何因子，纯转动拉曼高低阶通道信号比值可以表示为

不同量子数的转动拉曼微分后向散射截面可以通过下式计算得到：

式中：i为氧气或氮气分子；h为普朗克常数；c为光速；B0,i为分子在基态振动能级的转动常数；gi(J)为与核自旋Ii有 关的统计权重因子； ν0为激光发射波长的波数； γi为 分子偏振强度的各向异性参量；k为玻尔兹曼常数；T为大气温度； ∆νi为拉曼散射频移，可由式(4)计算得到；Erot,i为处于基态振动能级转动量子态为J的同核双原子分子所具有的转动能量，可由式(5)得到.

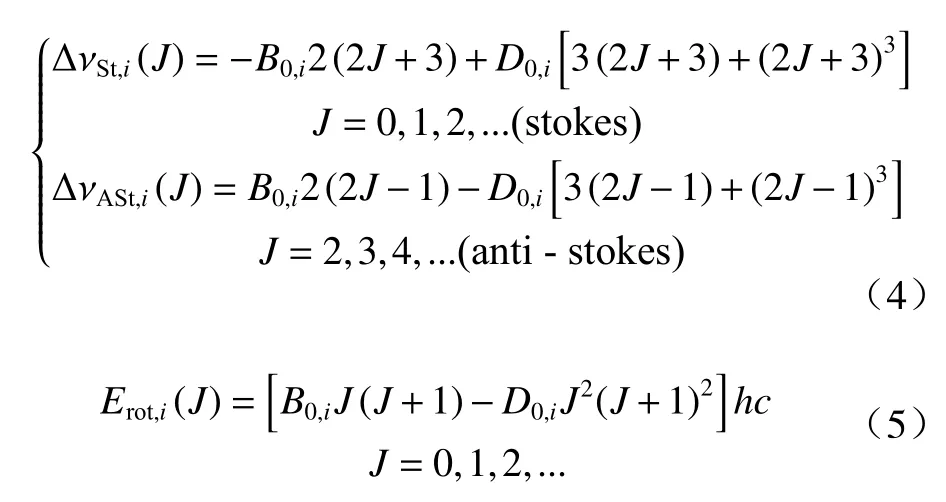
式中D0,i为分子在基态振动能级的离心畸变常数. 所用到的物理常数的具体数值如表1 所示.

表1 转动拉曼微分散射截面计算所需物理常数Tab. 1 Physical constants in the rotating Raman differential scattering cross section

因此，根据纯转动拉曼理论，代入探空温度，即可计算出高低阶通道有效微分散射截面之比X(T,z).通过高低阶拉曼信号比值R(T,z)与X(T,z)之比，可以得到：

式中CHL的取值仅与系统参数与物理常数有关，不随高度发生变化，因此可以通过对OR影响范围以外（OR(z)=1） 的CHLOR(z) 廓 线求均值后得到CHL，然后获得拉曼测温通道的残余几何因子OR(z)为

对拉曼信号比值进行残余几何因子修正后，利用二阶指数拟合法反演大气温度廓线：

式中A1、B1和C1为标定系数，可根据探空温度与信号比值进行拟合获得.

2 实验设备

采用北京理工大学设计研制的纯转动拉曼-米激光雷达[14]探测数据对本文提出的方法进行实验验证. 该系统可以同时接收米散射和转动拉曼散射信号，实现大气温度和气溶胶的同步探测. 其中，为了提高拉曼信号信噪比，高低阶通道接收对称分布的正反斯托克斯散射信号，中心波长分别为533.69、535.05、530.32 和528.98 nm. 其工作过程为：Nd:YAG激光器发射的532 nm 激光脉冲通过扩束器进行扩束、准直，然后经导光镜垂直进入大气； 激光和大气中的分子和气溶胶相互作用后，产生散射回波信号，由接收望远镜接收、聚焦后通过视场光阑进入光纤，随后导入双光栅单色仪进行分光；分光后的米信号和高低阶拉曼信号进入光电倍增管完成光电转换，分别由模拟采集卡和双通道光子计数卡采集并保存.

3 分析与讨论

选用转动拉曼-米激光雷达于2020 年11 月23日19:00−20:00 期间的观测数据对本文方法进行实验验证. 该天空气质量为优，大气中气溶胶含量较低，采集到的拉曼回波信号受米散射信号的影响可以忽略. 由于拉曼信号信噪比较低，用于标定残余几何因子的转动拉曼回波信号的积分时间选为50 min.

首先，根据实际测得拉曼通道中心波长和线宽（FWHM=0.65 nm），高斯拟合拉曼通道的归一化相对透过率，得到激光雷达系统拉曼通道光谱范围内氮气和氧气多个谱线的归一化透过率，如图1 所示.

图1 拉曼通道光谱范围内的归一化相对透过率Fig. 1 The normalized relative transmittance of Raman channel

然后结合南郊气象台使用探空气球在同一时间探测的大气温度数据计算高低阶通道的有效微分散射截面，从而获得X值. 通过计算得到的X值，由式（6）计算出CHLOR(z)，如图2 中黑色点线所示. 接下来求解CHL值，由于实测信号受各种噪声影响，信噪比较低，因此需要先对CHLOR(z)廓线进行去噪处理，此处采用变窗长滑动平均法. 滑动窗口的初始大小设为n=2k+1= 3(k=1)，窗长为90 m，每增加7 个数据点，滑动窗口在中心点的两边增加1 个点，即210 m 高度内的初始窗长 ∆z¯=n∆z=90 m，然后高度每增加210 m，滑动窗口上下各增加30 m. ∆z为激光雷达数据的初始垂直分辨率（30 m）；k为中心点两边的数据点个数；n=2k+1为滑动平均窗口大小，即决定滑动平均窗口长度的原始激光雷达数据点个数. 图2（a）中黑色实线为去噪后的CHLOR(z)廓线，从图中可以看到，1.5～5.0 km 范围内CHLOR(z)廓线近似不随高度变化，取该区间内的均值作为CHL值 ，计算得CHL=1.27，标准差为0.002 6，从而可以得到拉曼高低阶通道的残余几何因子廓线，如图2（b）所示. 可以看出，OR值在对流层底部明显偏离理论值1，表明信号存在较大的畸变，可能受两通道几何因子不同的影响，若不对拉曼比值廓线进行修正，势必会对温度反演引入较大误差.

图2 2020 年11 月23 日晚实测的C HLOR(z)原始廓线与去噪廓线以及残余几何因子廓线Fig. 2 Original profile and denoising profile of C HLOR(z) and residual overlap profile measured on Nov 23, 2020

由于拉曼信号信噪比较低，先利用变窗长滑动平均法对高低阶拉曼信号进行去噪，然后再进行标定和反演. 图3（a）给出残余几何因子修正前后的转动拉曼高低阶信号比值原始廓线和去噪廓线，可以看出修正后的比值廓线与高度之间有着近似线性关系，并且与探空温度变化趋势一致，从侧面可以说明数据修正结果的准确性. 然后根据探空参考温度，对修正前后的比值廓线进行标定和反演，为了避免近地面几何因子的影响，标定高度选取3～9 km，最终温度反演结果如图3（b）所示.温度反演精度以探空温度为标准用均方根误差来衡量，根据齐白玉等[15]研究得到该系统的探测盲区为0.18 km，因此计算了0.18～1.50 km 范围内温度的均方根误差. 从图中可以看到，未经过几何因子修正的温度反演结果在残余几何因子影响范围内的准确度较低，无法对近地面的温度分布进行描述，而由残余几何因子修正后的反演结果与探空温度之间具有良好的一致性，近地面反演精度大大提高，均方根误差从修正前的4.23 K 减小到0.64 K.

图3 2020 年11 月23 日残余几何因子修正前后的转动拉曼高低阶信号比值廓线，以及采用修正前后信号反演的大气温度廓线（图中标出的温度误差为0.18～1.50 km 范围内的均方根误差）Fig. 3 The signal intensity ratio profiles with and without residual overlap correction and their corresponding inversion temperature profiles on Nov. 23, 2020(temperature errors marked in the figure is the average value in the range of 0.18～1.50 km)

为了验证残余几何因子是否具有普适性，采用2020 年11 月23 日计算得到的残余几何因子，对系统参数设置一致、光路未发生变动和天气情况相似的多组激光雷达探测数据进行修正和反演，这里选用的2020 年11 月24 日、26 日和27 日夜间数据.

对选用的拉曼信号进行残余几何因子修正，并通过同样的预处理、标定和反演流程，最终得到的结果如图4 所示. 图4（a），4（c），4（e）为残余几何因子修正前后的拉曼信号比值廓线，图4（b），4（d），4（f）为利用修正前后的比值廓线反演得到的温度廓线，并给出0.18～1.50 km 范围内温度的均方根误差. 结果表明，新方法计算得到的残余几何因子具有一定的普适性，且修正残余几何因子后的拉曼信号，在残余几何因子影响范围内温度反演精度大大提高，反演误差减小到1 K 左右.

图4 2020 年11 月24 日、26 日和27 日修正前后高低阶拉曼信号比值廓线及对应的温度反演廓线（图中标出的温度误差为0.18～1.50 km 范围内的均方根误差）Fig. 4 The signal intensity ratio profiles with and without residual overlap correction and the corresponding inversion temperature profiles on Nov. 24, 26 and 27,2020 (temperature errors marked in the figure is the average value in the range of 0.18～1.50 km)

4 结 论

本文提出一种拉曼-米激光雷达测温通道的残余几何因子修正的方法. 该方法在拉曼信号中建立一个与有效微分散射截面相关的因子，可由探空温度和标定的归一化光谱透过率确定. 在此基础上，标定得到测温通道的残余几何因子. 然后，利用北京理工大学激光雷达实验室研制的拉曼-米激光雷达探测数据对该方法进行实验验证. 实验结果表明，该方法能较好地修正残余几何因子对温度反演的影响，使近地面1.5 km 探测范围内温度均方根误差降至1 K左右. 在不改变系统硬件设备和光路的情况下，新方法得到的残余几何因子具有一定的普适性，有助于提高转动拉曼-米激光雷达探测性能，使边界层内的温度测量更加精确.