基于非等壁厚药型罩的准球形爆炸成型弹丸成型因素研究

李元，谢佳良，张浩宇，温玉全

（1. 西北工业大学 极端力学研究院，陕西 西安 710072；2. 空军装备部 驻沈阳地区军事代表局驻吉林地区军事代表室，吉林 吉林 132021；3. 北京理工大学 爆炸科学与技术国家重点实验室，北京 100081）

爆炸成型弹丸（explosively formed projectiles，EFP）也被称为自锻破片（self-forging fragments，SFF），是成型装药的一种[1]. 相对于聚能射流，爆炸成型弹丸的药型罩曲率较大，可以形成长径比相对小的弹丸. 具有对炸高不敏感、药型罩质量利用率高和侵彻孔径大、后效作用大等优点，适用于远距离打击轻型装甲目标和软目标，如攻击装甲车辆顶部的末敏弹所采用的毁伤元就是EFP. 长杆形EFP 有利于提高对目标的穿深，但是其在飞行过程中的稳定性不好. 尾裙杆式EFP 和尾翼式EFP 可以一定程度上提高EFP 的飞行稳定性，但是空气阻力较大. 相对于尾裙杆式EFP 和尾翼式EFP，球形EFP 飞行时速度衰减系数较小[2]，且其飞行姿态对其弹道影响不大[3]，因此球形EFP 的长距离打击精度更高. 另外准球形EFP 的形态为实心的密实结构，侵彻孔径和后效威力较大，侵彻特性好于某些空心EFP 结构[4]. 尽管相对于长杆稳定EFP，准球形EFP 的侵彻深度不大，但是在冲击加载试验[5]、防空反导[2]、深空撞击探测[6]等领域依然有较大的应用价值. 目前关于准球形EFP 的研究报道较多. 杨军等[3]数值模拟研究了一种准球形爆炸成型弹丸的形成、飞行和侵彻过程，研究了药型罩外曲率变形对EFP 的速度和形状的影响. 王树友等[7−8]采用杨军的结构进一步仿真研究了药型罩中心壁厚和外曲率半径对EFP 速度和长径比的影响规律，并进行了靶场的试验验证. 针对目前准球形EFP 的成型因素研究较少的情况，王伟等[9−10]进一步研究了装药结构的其他因素对准球形EFP 成型的影响规律.杨军等[3]、王树友等[7-8]和王伟等[9−10]所研究的装药结构相同，如图1 所示. 该结构利用专门的挡环来改变EFP 的形状，但是他们的研究并未考虑挡环的厚度和高度这两个重要因素. 挡环的使用势必增加相关的成型影响因素数量和弹药重量，而文中的研究表明不采用挡环依然能够形成形态良好的准球形EFP. 此外，当前的研究也未将准球形EFP 的侵彻特性（比动能指标）考虑进去. 因此，考虑到成型装药是一个各因素高度耦合的复杂系统，需要对准球形EFP 的成型做进一步地系统研究.

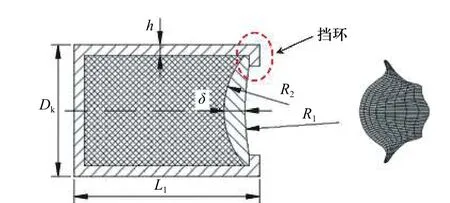
图1 采用挡环的EFP 装药结构示意图Fig. 1 Schematic diagram of charge structure with baffle ring

文中基于试验验证过的数值模型，研究一种不采用挡环的非等壁厚药型罩形成准球形EFP 问题.进行了多因素水平和多指标的正交优化设计，从而系统的研究准球形EFP 成型过程中各个因素以及各水平对EFP 速度、比动能和长径比等的影响规律，并进行了各因素的敏感性分析，得到了最优的准球形EFP 设计方案. 本研究可以为准球形EFP 的设计和优化提供重要参考.

1 装药结构及正交设计

采用非等壁厚的球缺形药型罩结构，如图2 所示. 影响爆炸成型弹丸的因素有装药的长径比L/D、壳体厚度h、药型罩的内外曲率R1和R2、以及药型罩的中心壁厚等. 将装药长径比、药型罩内外曲率以及药型罩中心厚度作为设计变量，而将壳体厚度、装药直径等作为不变量. 取壳体厚度为1.2 mm，背板厚度0.8 mm，装药直径为20 mm. 壳体材料为硬铝，装药为JH-2 炸药（8701 炸药），药型罩材料为紫铜.起爆方式为底面中心起爆.综合考虑EFP 的侵彻特性，取试验指标为EFP速度、比动能和长径比L/D. EFP 比动能定义为动能与轴向最大横截面积的比值. EFP 长径比l/d取为EFP 外轮廓最长轴向尺寸与外轮廓最大直径的比值.研究装药长径比L/D，药型罩的内外曲率R1和R2，以及药型罩的中心壁厚S等对试验指标的影响. 因此共有4 个因素，每个因素取4 个水平，如表1 所示.

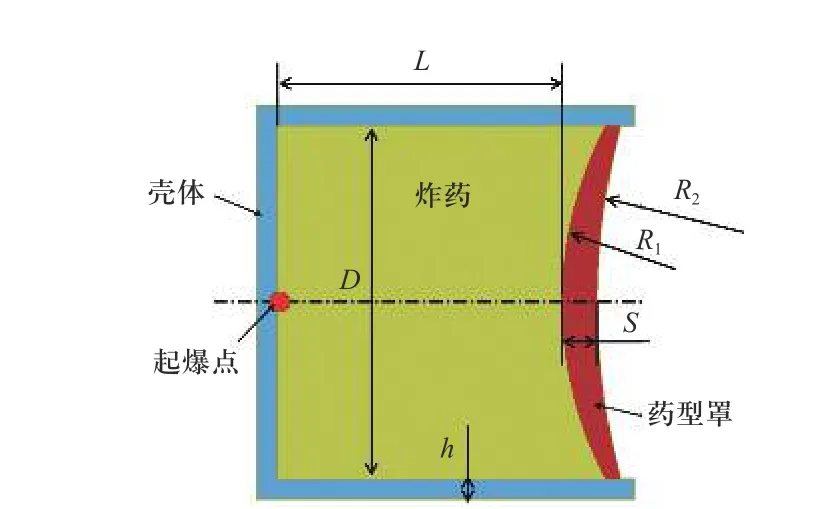
图2 战斗部结构示意图Fig. 2 Schematic diagram of Warhead structure

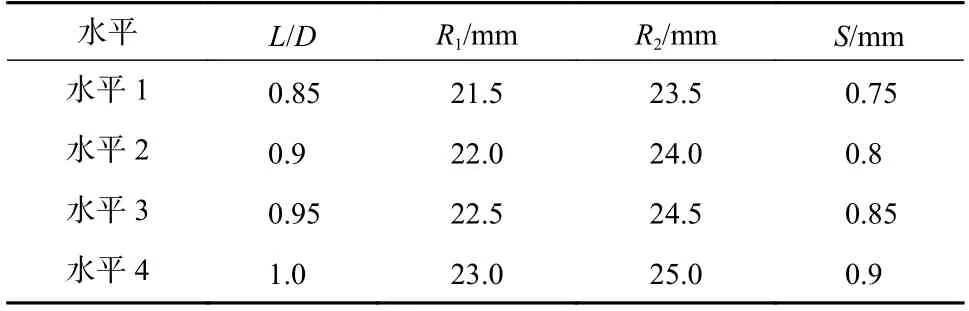
表1 因素及各水平数Tab. 1 Factors and their levels

为此，选取L16(45)正交表来安排实验[11]，实验安排如表2 所示.

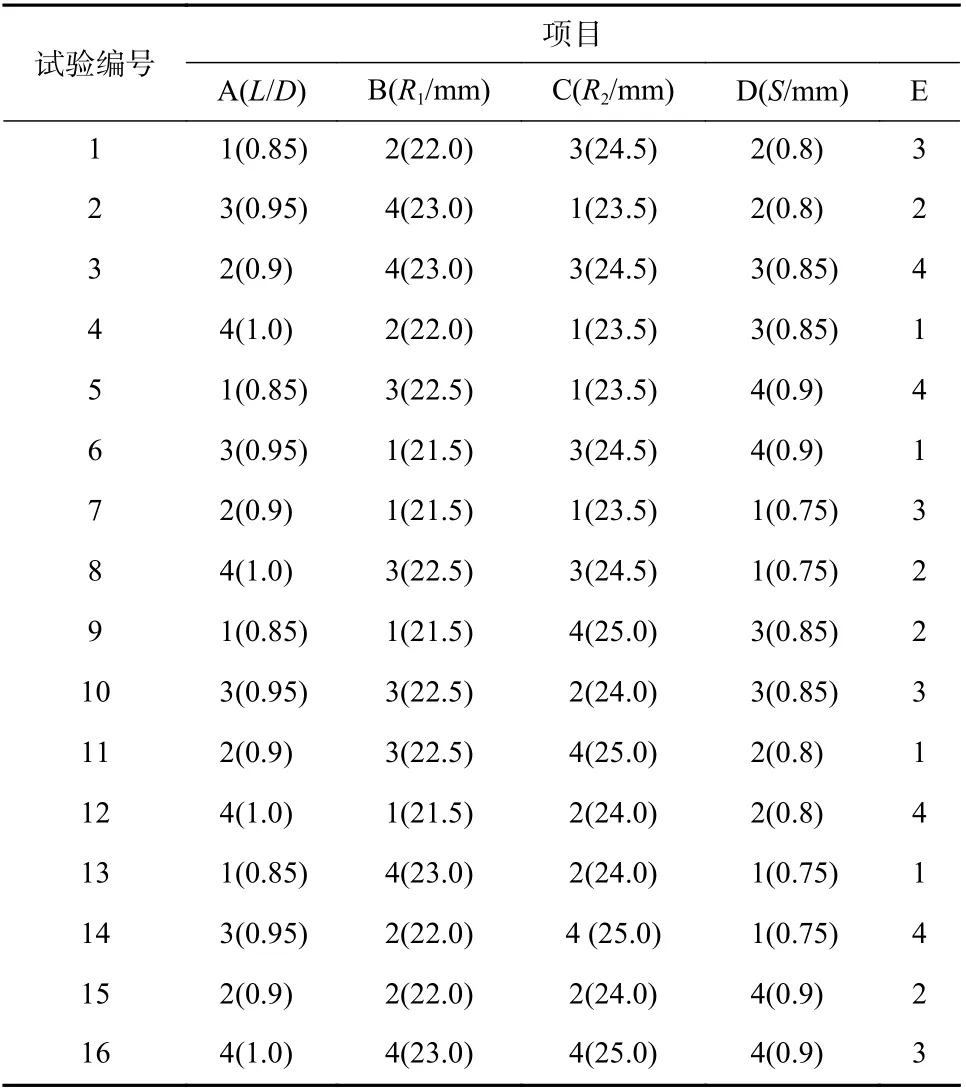
表2 设计的正交表Tab. 2 Designed orthogonal optimization table

2 优化设计试验

材料参数、仿真算法等对有限元计算结果精度具有重要影响. 为了得到可靠的优化结果，需要首先对建立的模型进行试验验证. 进而依据验证过的有限元模型，进行正交优化的虚拟试验设计. 此外，准球形EFP 的形成过程既非向前翻转成型也非向后翻转成型，而是类似射流的成型过程−药型罩外曲面（远离炸药一侧）向前运动而内曲面（紧贴炸药一侧）向后运动. 因此需要选取具有类似成型特点或者准球形EFP 的试验结果进行模型验证.

2.1 模型验证

李伟兵等[12−14]系统的研究了一种弧锥结合形药型罩的双模聚能装药成型和侵彻特性，且给出了装药结构尺寸和试验结果. 本研究基于文献[12 − 14]的装药结构，建立了有限元模型，并将计算结果与试验结果进行对比验证. 李伟兵等[12]研究的战斗部结构如图3 所示，其中药型罩锥角为145°，锥顶圆角半径为45 mm，药型罩厚度为2.8 mm. 装药为JH-2 炸药，药型罩为紫铜，壳体为45 钢. 利用ANSYS APDL 建立该结构的有限元模型，如图4 所示. 由于结构为中心轴对称，因此为减小计算量采用二维轴对称模型.炸药起爆由LS-DYNA 的起爆点设置关键字实现. 壳体、炸药和药型罩统统采用Lagrange 算法，并设置各Part 之间的接触方式为二维的自动面面接触. 装药JH-2 炸药采用High-Explosive-Burn 本构模型和JWL状态方程. 药型罩紫铜采用Steinberg 本构模型和Gruneisen 状态方程. 壳体45 钢选用Johnson-Cook 本构模型和Gruneisen 状态方程. 计算中所使用的各材料参数见文献[15].仿真计算得到的EFP 形状和试验得到的X 光照片对比如图5 所示，具体的速度、尺寸参数对比见表3 所示从图5 可以看出，仿真计算得到EFP 形态与试验结果吻合较好. 仿真结果再现了EFP 的尾裙以及头部的“水滴”特征. 由于采用的算法为Lagrange 算法，因此计算结果无法得到EFP 后部跟随的破碎体.从表3 所示的EFP 速度和尺寸可以看出，仿真得到的EFP 速度相对于试验结果的误差为−7.26%. 100 μs时计算得到EFP 的长度和外径相对试验的误差分别为4.45%和−8.28%，而140 μs 时的相对误差分别为1.57%和−27.46%. 除了140 μs 外径的误差较大之外，其他参数仿真计算与试验结果吻合较好. 为了进一步验证仿真算法的准确性，对Teng 等[5]试验研究的准球形EFP 装药结构（如图6(a) (b)所示）也进行了仿真分析. 装药采用Octol 炸药，药型罩材料为纯铁，药型罩固定环材料为钢，而雷管座为塑料. 所建立的有限元模型如图6(c)所示. 采用LS-DYNA 轴对称模型.装药Octol 炸药采用High-Explosive-Burn 本构模型和JWL 状态方程. 药型罩纯铁和固定环钢材料（Steel 1006）选用Johnson-Cook 本构模型和Gruneisen状态方程.雷管座塑料采用Piecewise-Linear-Plasticity 本构模型.相关的材料参数取自AUTODYN 软件材料数据库[16].试验和仿真得到150 μs 时准球形EFP 如图7 所示.

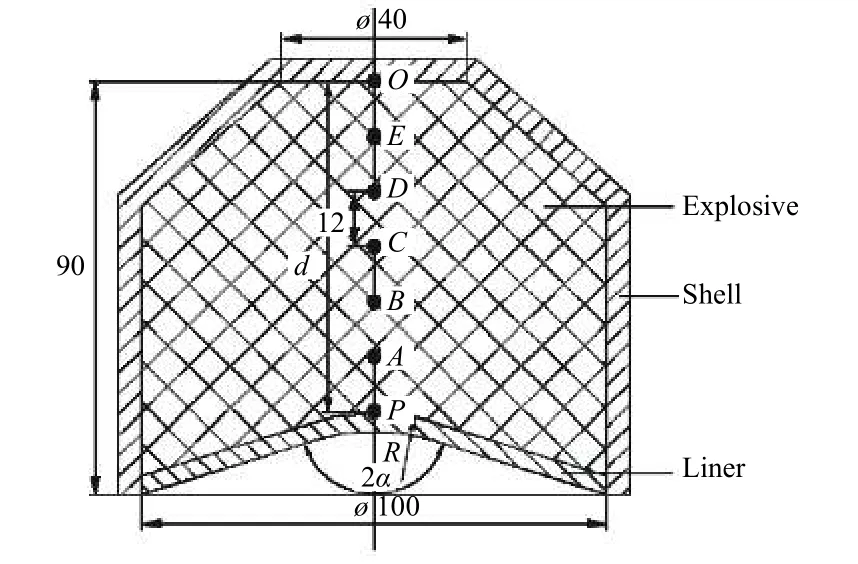
图3 弧锥罩装药结构示意图[12]Fig. 3 Schematic diagram of charge structure of LI Wei-bing[12]

图4 验证模型Fig. 4 Model for validation

图5 仿真和试验得到的EFP 形态对比Fig. 5 Comparison of the EFP shapes between simulation and experiment

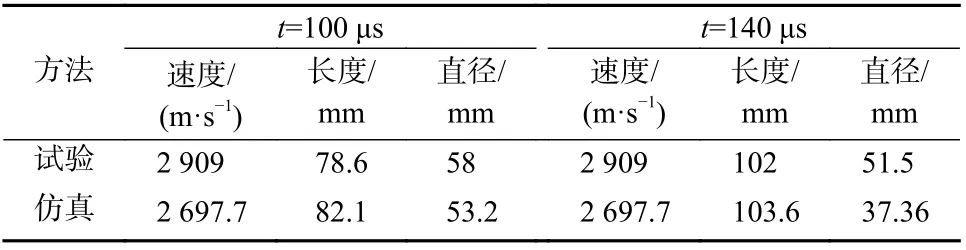
表3 EFP 速度和尺寸Tab. 3 EFP velocity and size

图6 弹丸发生器尺寸、样机及有限元模型Fig. 6 Diagram, photograph and element model of the projectile generator

图7 150μs 时EFP 形态对比Fig. 7 Comparison of the EFP profiles at 150μs

从图7 可以看出，仿真得到的EFP 形状与试验吻合较好. 同时速度计算结果也与试验吻合，仿真得到的EFP 速度为2 380 m/s，而试验得到的EFP 速度为2 474 m/s，相对误差仅为−3.8%. 两个试验结果验证表明本仿真所采用的材料模型、算法设置等较合理，可以作为进一步研究的基础.

2.2 正交优化试验

基于上一步验证过的材料参数、算法设置等，建立图2 所示装药结构的有限元模型，如图8 所示.同样采用二维的轴对称算法. 装药采用JH-2 炸药，药型罩材料为紫铜（炸药和紫铜材料参数取值同3.1 节李伟兵装药结构模型），而壳体材料为硬铝，采用PLASTIC-KINEMATIC 本构模型，材料参数取自文献[17].

图8 弧锥罩有限元模型Fig. 8 Finite element model of arc-taper liner

根据表2 所设计的正交表，分别设置不同的长径比、药型罩曲率等进行计算，得到不同因素和水平下的EFP 性能指标，即速度、比动能和长径比，如表4 所示. 同一因素水平下计算得到的指标值进行加和平均，依次填入表5 的Ⅰ、Ⅱ、Ⅲ和Ⅳ（对应每个因素的4 个不同水平），表示指标随因素的变化趋势. 将Ⅰ、Ⅱ、Ⅲ和Ⅳ的最大值和最小值相减，得到极差Rj，反映因素对指标的影响大小.

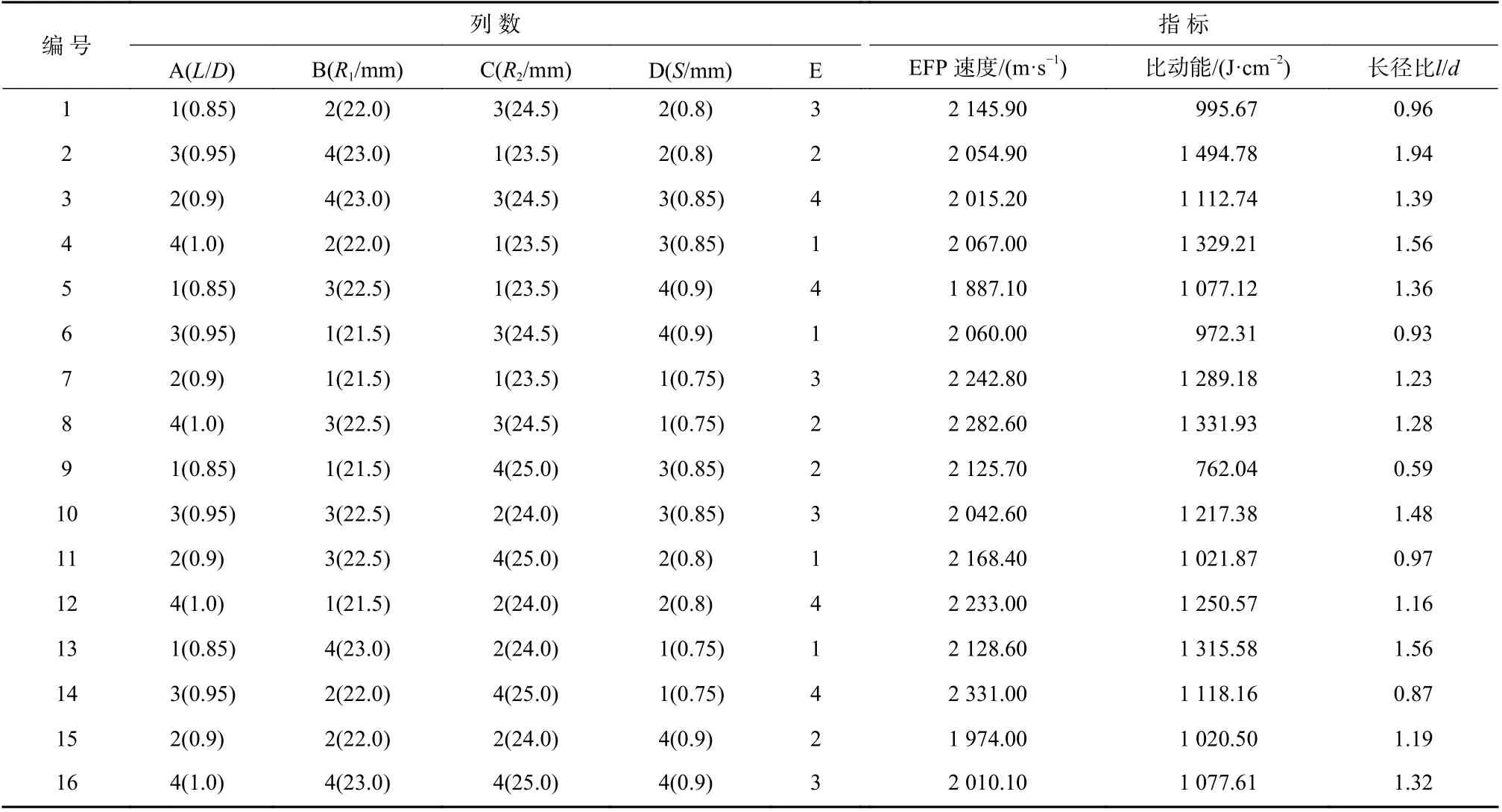
表4 不同因素下的计算结果Tab. 4 Results of different factors and levels

对于多指标值的问题，正交实验设计有两种数据处理方法，一种是对各个指标结果加权求和，再将求和按单指标的计算，称为综合评分法. 另一种是先把各个指标按单一指标进行分析，然后再把对各个指标计算分析的结果进行综合平衡，从而确定各因素水平的最优或较优组合，称为综合平衡法. 采用第二种分析方法进行结果分析. 将表5 中不同指标对应于不同因素的Ⅰ、Ⅱ、Ⅲ和Ⅳ绘于图9 中.

表5 计算结果极差分析Tab. 5 Range analysis of results

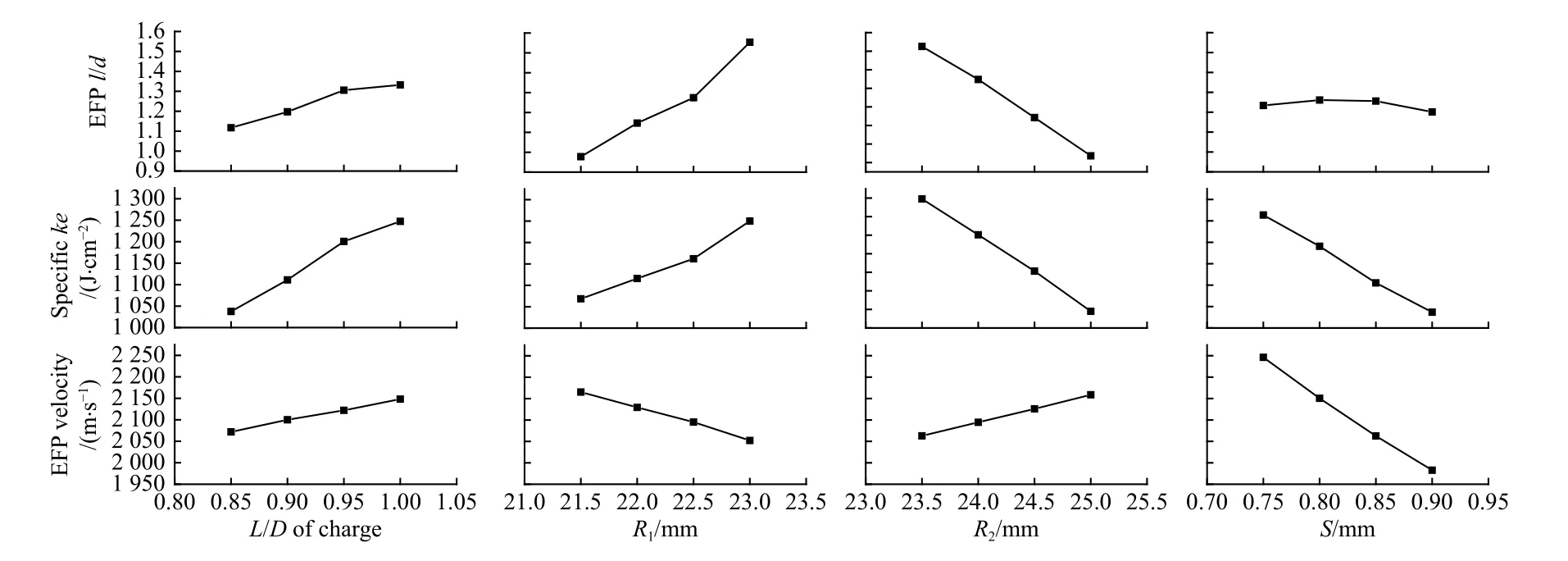
图9 指标随因素水平的变化Fig. 9 Evaluation index vs. factor levels

从图9 的变化趋势可以看出，EFP 长径比随着装药长径比和药型罩内曲率半径R1的增大而增大，随着药型罩外曲率R2的增大而减小，而药型罩中心厚对EFP 长径比的影响不大. EFP 比动能随着装药长径比和药型罩内曲率半径R1的增大而增大，随着药型罩外曲率R2和药型罩中心壁厚S的增大而减小.EFP 速度随着装药长径比和药型罩外曲率半径R2的增大而增大，随着药型罩内曲率R1和药型罩中心厚度S的增大而减小.

从表5 中的Rj极差值和图9 看出，对于EFP 速度，药型罩中心壁厚的影响最大，且厚度越小，EFP速度越大，取0.75 mm 厚度为宜，而其他因素影响程度相差不多；对于比动能，药型罩外曲率半径R2影响程度最大，而R2对EFP 的速度影响不大，所以可取R2=23.5 mm，而其他各个因素影响程度相当；对于EFP 长径比，要求接近于1，内外曲率半径R1、R2对其影响相当，装药长径比次之，中心壁厚影响最小.综合考虑，取L/D=0.9，R1=21.5 mm，R2=23.5 mm，S=0.75 mm. 即最优实验水平号为2 1 3 1. 已做水平组合中并没用这一水平，重新计算的此水平组合结果为：v=2 311.9 m·s−1，比动能ke=1 106.84 J·cm−2，长径比l/d=1.04. 此时的EFP 形态如图10 所示，EFP 成型较为密实，且EFP 比动能、速度和长径比达到了较为协调的程度. 此外，此准球形EFP 形态与高超等[2]的试验结果相似. 如图11 所示，尽管高超的具体装药结构参数未知，但可判断其装药结构未采用挡环且是经过精心设计的. 进一步证明了相关计算和优化的准确性.

图10 优化得到的准球形EFPFig. 10 Quasi-spherical EFP from optimization

图11 高超等[2]的试验结果Fig. 11 Experimental results of GAO’s work[2]

由于EFP 的成型过程满足相似率原理[18]，因此在保持材料相同的情况下，本研究所优化得到的EFP 最优设计可以缩放到任意尺寸的准球形EFP 装药，为准球形EFP 的设计提供了参考.

2.3 影响因素讨论

王伟等[10]优化得到的指标随影响因素的变化趋势如图12 所示（装药、药型罩材料等与本研究相同）. 从图12 中可以看出，相比于装药长径比L/D，药型罩内外曲率R1和R2对EFP 动能的影响不大，药型罩中心壁厚S的影响也较小. 对于EFP 长径比，药型罩曲率R2的影响不大，这与文中的研究结果不同，如图9 所示. 本研究得到的因素对EFP 长径比的影响大小顺序为R2>R1>L/D>S，而王伟得到的影响顺序为L/D>R1>S>R2. 可见，是否采用挡环对准球形EFP的成型规律具有较大影响.

图12 王伟的结果[10]Fig. 12 Results of WANG’s work[10]

顾文斌等[19]对非等壁厚的药型罩成型进行了正交优化设计研究，以EFP 长径比、比动能和速度为优化指标，旨在寻求具有较大威力的长杆EFP. 顾文斌得到的指标随不同影响因素的变化情况如图13 所示.

对比图13 和图9 可以看出，EFP 性能指标随着影响因素的变化趋势与文中的研究结果相同. 这是由于我们采用了相同的装药结构和药型罩结构. 但是，各因素对指标的影响大小并不相同，对于EFP 长径比，顾文斌的影响大小顺序结果为L/D>R2>R1>S，而文中准球形EFP 的结果为R2>R1>L/D>S；对于EFP比动能，顾文斌的影响大小顺序结果为L/D>R2>R1>S，而文中准球形EFP 的结果为R2>S>L/D>R1；对于EFP速度，顾文斌的影响大小顺序结果为S>L/D>R2>R1，而文中准球形EFP 的结果为S>R1>R2>L/D. 可见，即使装药结构相同，为了得到不同形状的EFP，各因素对EFP 的成型也具有不同的影响规律，即各因素在不同形状EFP 成型过程中所起到的作用大小在发生变化. 如为了控制长杆EFP 的长径比，调整装药的长径比L/D效果要优于调整其他因素. 这是因为形成长杆EFP 需要较大的轴向驱动冲量，而装药的长径比L/D正是控制轴向驱动冲量的关键因素；而对于准球形EFP 的长径比，可优先调整药型罩的外曲率半径R2. 这是因为形成准球形EFP 需要减小EFP 的轴向速度梯度，增大药型罩中央处的质量汇聚，而外曲率半径R2可以很好地调整这两点. 此外，在文中研究得到的最优准球形装药结构基础上，采用端面面起爆也可以形成长径比较大的EFP 毁伤元（如图14 所示），因此该装药结构可作为多模战斗部使用.

图13 顾文斌的结果[19]Fig. 13 Results of GU’s work[19]

图14 面起爆形成的EFPFig. 14 EFP formed by face initiation

3 结 论

文中针对某准球形爆炸成型弹丸的成型问题，利用试验验证过的有限元模型，系统地研究了相关因素的影响. 除EFP 长径比随着药型罩中心的厚度变化不大外，EFP 长径比和比动能随着各因素的变化趋势基本相同. EFP 长径比随着装药长径比和药型罩内曲率半径R1的增大而增大，随着药型罩外曲率R2的增大而减小. EFP 长径比随因素的变化趋势与采用挡环时的准球形EFP 不同，是否具有挡环对准球形EFP 的成型规律影响较大；EFP 比动能和速度随着装药长径比和药型罩中心厚度的变化规律相同，而随着药型罩内、外曲率的变化趋势相反. EFP比动能随着装药长径比和药型罩内曲率半径R1的增大而增大，随着药型罩外曲率R2和药型罩中心壁厚S的增大而减小；对于EFP 速度，药型罩中心壁厚的影响>药型罩内曲率>药型罩外曲率>装药长径比；对于比动能，药型罩外曲率半径影响程度>药型罩中心厚度>装药长径比>药型罩内曲率；对于EFP 长径比，要求接近于1，内外曲率半径R1，R2对其影响相当，装药长径比次之，中心壁厚影响最小；由于采用相同的装药结构和非等壁厚药型罩结构，准球形EFP 优化指标随着因素的变化趋势与长杆式EFP 的优化结果相同，但是因素的影响程度大小顺序与长杆EFP情况截然不同. 对于不同形状的EFP，各因素的影响规律是不同的.