基于分段的渔船轨迹相似性度量的研究

李 爽，李 然

（大连海洋大学 信息工程学院，辽宁 大连 116000）

0 引 言

渔船的轨迹数据记录着渔船的位置、经度、纬度等。通过总结渔船航行特点、轨迹模式等，能够为渔船行为识别、渔船状态监控、海上交通规划等提供理论支持和技术支撑。从2002 年至今，安装船舶自动识别系统（Automatic Identification System，AIS）的设备逐渐增多，它在保障船舶安全航行方面起到了显著作用。

随着航运经济的发展，个体船舶大量增加，个体经营人从事船舶运输，拓宽了航运投资渠道，但个别个体经营人由于经营素质不高，从事海上违法行为，普遍采取“一船多码”，非法套用他人AIS 设备的经营方式。“一船多码”会给船舶使用带来诸多不便，严重干扰船舶协调避碰及安全通信，给海事监管、港口正常船舶调度及应急搜救等工作带来极大障碍，所以有效地识别“一船多码”的船舶十分必要。利用AIS 获悉到的数据包含船舶航行多个维度的信息，通过分析大量渔船AIS 轨迹数据为渔船可疑行为检测提供了理论基础。

在船类轨迹相似度研究方面，文献[13]提出基于分段动态规划的渔船AIS 轨迹相似性度量算法。文献[14]提出基于Gromov⁃Hausdorff 距离和信息融合权值，计算不同舰船轨迹对应的度量矩阵集合之间的Gromov⁃Hausdorff 距离。

上文中列举的算法均直接应用轨迹间距离进行相似性度量，对数值较为敏感，需要对完整轨迹进行度量，本文采用余弦相似度进行度量，其对轨迹的完整性不敏感，不会因为待度量轨迹的部分缺失而影响轨迹度量效果。针对上述研究的局限性，本文在对轨迹进行相似性度量前，对轨迹进行了间隔采样，采样后的点形成的轨迹既能保留渔船运动的原始形态，也能减轻后续计算的复杂度。在进行相似性度量时，对轨迹进行了分段处理，依次比较每一段的相似性，采取分段的方法，减少了因轨迹缺失对度量造成的影响。

1 理论模型的构建

1.1 相关定义

轨迹点（Trajectory Point）：是由传感器采集的船只位置数据，是一条多维数据，即：

轨迹（Trajectory）：是由一系列按照时间顺序排列的轨迹点的集合，即：

式中：表示一条渔船轨迹；为轨迹点的个数。

轨迹片段（Trajectory Segment）：是轨迹中按时间序列排序的一条连续的轨迹段，本文中主要是指在某一时间区域内的轨迹点构成的轨迹段。

经度差值（Longitude Difference）和纬度差值（Latitude Difference）：已知相邻的轨迹点p=(x,y,t)和p=(x,y,t)，将两点的经度和纬度做差，得到经度差值Δx，纬度差值Δy，即：

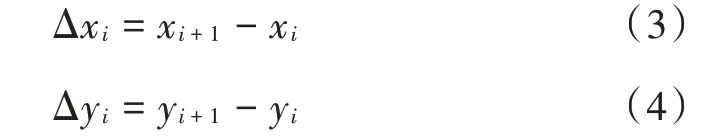
精准率：精准率是正确检索出的相似轨迹数与检索出的相似轨迹数的比值。

召回率：召回率是正确检索出的相似轨迹数与轨迹库中所有相似轨迹数的比值。

1.2 余弦相似度

余弦相似度（Concosine Similarity）：指一个向量空间中两个向量的夹角余弦值作为评估两个个体之间的相似度。两个向量之间的余弦值越大，则两个向量越相似。

以维空间为例，向量是[,,…,x]，向量是[,,…,y]，则与夹角的余弦cos的计算公式如下：

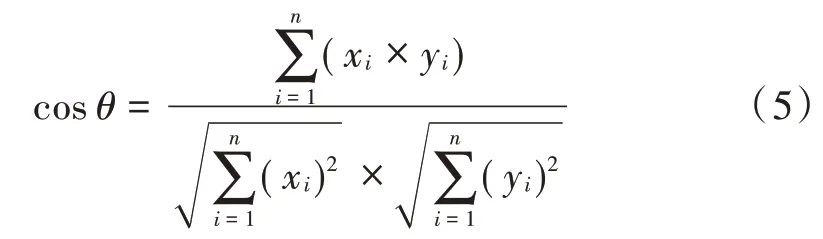
1.3 轨迹点矩阵的生成和轨迹点库的构建

1.3.1 轨迹点库的构建

向量空间模型（Vector Space Model，VSM）作为算法实现的数学模型基础。在算法使用的向量空间模型中，将预处理后的轨迹数据看作是由轨迹点(′,′,…,′)构成。因此，在轨迹库中的条轨迹组成的集合为={,,…,D}，构建的×的轨迹矩阵为，中的每个元素为a，定义为轨迹点发生在轨迹中的权重频率。矩阵的列向量(,,…,a)称为该轨迹库的轨迹向量，确定了该轨迹库所有轨迹，的行向量(,,…,b)称为该轨迹库的轨迹点向量，确定了该轨迹库所有轨迹点，即：

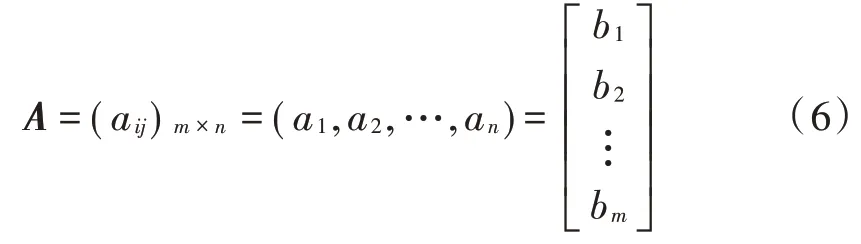
把轨迹库中的轨迹点和轨迹都编码为维向量空间中的向量，则轨迹库所有轨迹集合为：

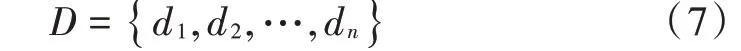
1.3.2 轨迹点矩阵的构建

轨迹点矩阵的特征值a由轨迹点在轨迹中的局部权重L以及平衡修正因子d两部分组成，即：

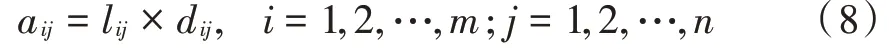
局部权重的计算方法是将轨迹点在轨迹中出现的次数除以轨迹的总轨迹点数。局部权重L为：

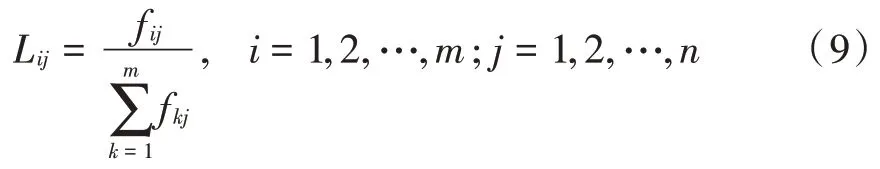
对局部权重因子L的平衡性修正的目的是在选择考虑局部权重计算公式时，尽可能地提高该权重因子的轨迹区分度。为了接下来的描述方便，需要定义二值函数：

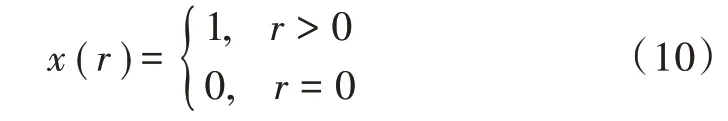
利用轨迹中出现最多的轨迹点作为基准对局部权重进行平衡性修正，这样就可以避免轨迹长度对局部权重产生的不利影响，L的表达式为：

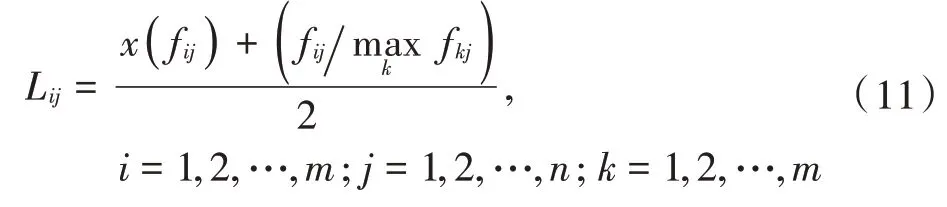
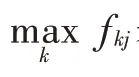
2 渔船轨迹相似性度量的模型研究

2.1 数据集描述

本实验原始数据集来自大连世想海洋科技有限公司2017 年10 月1 日—10 日渔船的轨迹数据，数据集中包含着丰富的渔船运动信息，如MMSI 码、时间、经度、纬度等，该文件以.csv 的格式进行存储，总计60 条渔船，整理后共计803 条AIS 轨迹数据，部分原始轨迹数据样例如表1 所示。

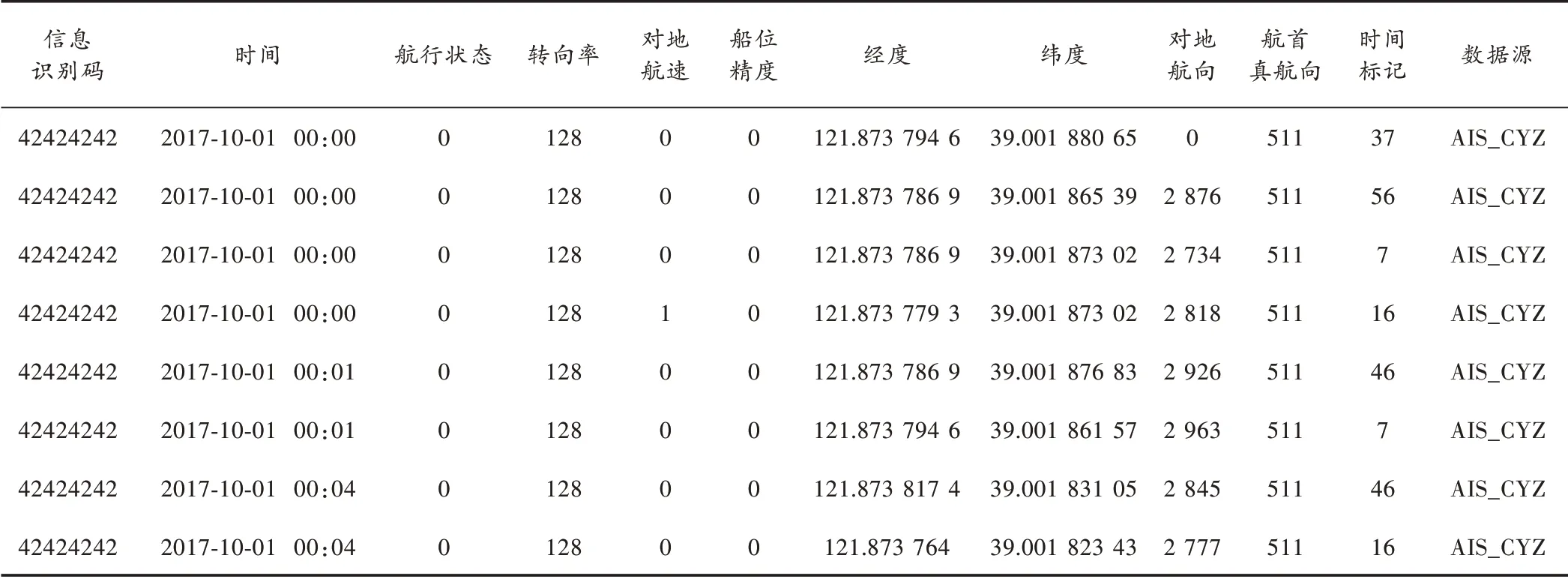
表1 原始轨迹数据样例

2.2 数据预处理

将采集到的船舶轨迹数据由.csv 格式转换成.xls 格式进行存储。在对轨迹进行重采样前，为了保证后续轨迹点选取的精度，删除MMSI 码异常的噪声数据，如MMSI 码为0 或者MMSI 码位数不正常的数据；删除不在研究水域中的数据等。在对轨迹进行重采样验证时，只需选取算法中涉及到经度、纬度、MMSI 码、时间等数据；在对轨迹进行分段相似性度量时，当采集到轨迹点同一时刻有多个数据时，只需随机选取一点，如果同一时刻重采样得到点经纬差值和小于0.03，则认为其为一个点。

2.3 重采样实验

轨迹的重采样控制轨迹的疏密程度，重采样后的渔船轨迹数据可以提高后续相似性度量算法的效率，本实验分别对轨迹数据进行间隔5 min、10 min、15 min 采样。图1 为一条原始渔船的轨迹，由282 个点组成；图2~图4 分别为经过5 min、10 min、15 min 等间隔采样得到的渔船轨迹。从图中可以清晰地观察到15 min 间隔采样破坏了轨迹原始形态，故后续实验不进行度量效果验证，直接舍去。5 min 间隔和10 min 间隔采样后的渔船轨迹都可以很好地保留原始轨迹的特征与形态，且轨迹点分布均匀，但是10 min 间隔采样较5 min 节省了时间，故此算法选择10 min 作为间隔采样的标准。

图1 原始渔船轨迹

图2 5 min 间隔采样渔船轨迹

图4 15 min 间隔采样渔船轨迹

图3 10 min 间隔采样渔船轨迹

2.4 基于分段的渔船余弦相似性度量算法实验

2.4.1 实验设计

对原始轨迹重采样是为度量轨迹间的相似性做准备，然后在式（6）~式（11）的基础上，根据以下算法流程图进行基于分段的渔船余弦相似性度量。算法流程图如图5 所示。

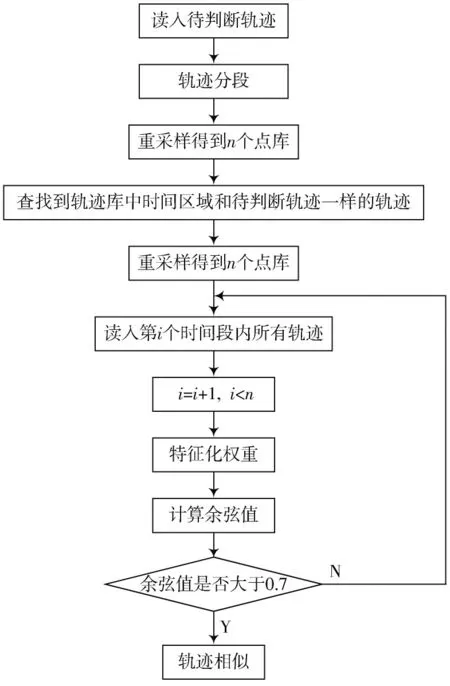
图5 算法流程图

步骤1：读入待判断轨迹，将待判断轨迹进行分段，分段时间间隔为4 h，得到对应的条子轨迹段，将这条子轨迹预处理，进行等时间间隔采样，同时，对于每个时间点可能出现的多个轨迹点随机采样一个点，得到对应的个点库。

步骤2：对轨迹库中同时间区域的轨迹和待判断轨迹一样进行同样时间间隔的分段，同样频率的采样，得到对应的轨迹点库。

步骤3：读入待判断轨迹第1 个子轨迹段的点库，利用式（11）计算第1 个子轨迹段点库中的点与该时间段点库中所有轨迹段对应轨迹点的特征化权重。

步骤4：求待判断轨迹段特征化权重向量与该时间段内轨迹库中所有轨迹段特征化权重向量的余弦值。

步骤5：如若第一个时间段区域内没有找到与其相似的渔船轨迹，依次读入待判断轨迹第2~第个子轨迹段的点库，利用式（11）计算第2~第个子轨迹段点库中的点与该时间段内点库中所有轨迹段对应的轨迹点的特征化权重，求待判断轨迹段特征化权重向量与该时间段内轨迹库中所有轨迹段特征化权重向量的余弦值，直到找到与其相似的轨迹段，轨迹相似性度量终止。在本实验中设置余弦值大于0.7，即认为两条轨迹为相似轨迹，如果所有时间区域内的轨迹都没有相似的，则证明该条轨迹不是异常轨迹，只是一条正常行驶的轨迹。

2.4.2 实验对比与讨论

本文先选用两种验证方式作为对比实验来验证最佳的间隔采样以及轨迹分段方式，两种方式的实验数据集完全一样，该实验结果以余弦相似度的值以及CPU的运行时间作为参考，余弦值越接近于1，表示越相似。同时采用精准率和召回率的方式来证明轨迹存在信号缺失或者AIS 关闭时，等时间间隔采样条件下分段与不分段对结果带来的影响，该实验结果以精准率和召回率作为参考，精准率和召回率越高，度量效果越好。实验数据集为200 条待判断轨迹。

1）在对轨迹进行5 min 间隔采样的前提下，对比分段以及不分段的余弦值以及CPU 运行时间，如表2 所示。从表2 可以看出，在对轨迹进行5 min 等间隔采样的前提下，对待判断轨迹进行相似性度量，经过分段的轨迹要比没有进行分段的轨迹CPU 运行时间平均提高了29.8 倍，原因是在分段度量时，如果该段度量余弦值达到0.7 以上，相似性度量便终止，无需度量完整轨迹。

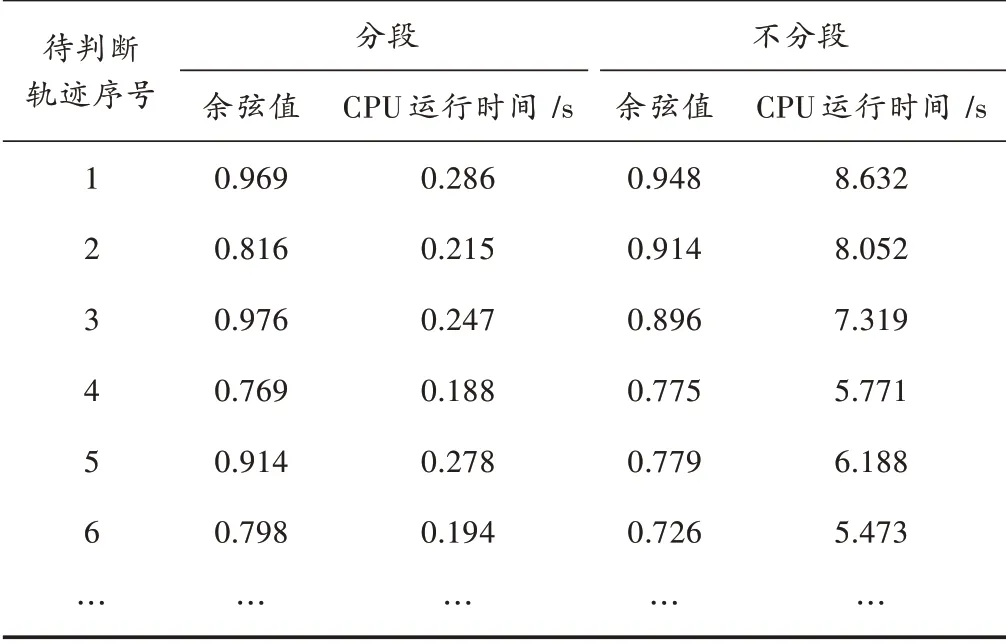
表2 5 min 间隔采样对比实验

2）在对轨迹进行10 min 间隔采样前提下，对比分段以及不分段的余弦值以及CPU 运行时间，如表3所示。

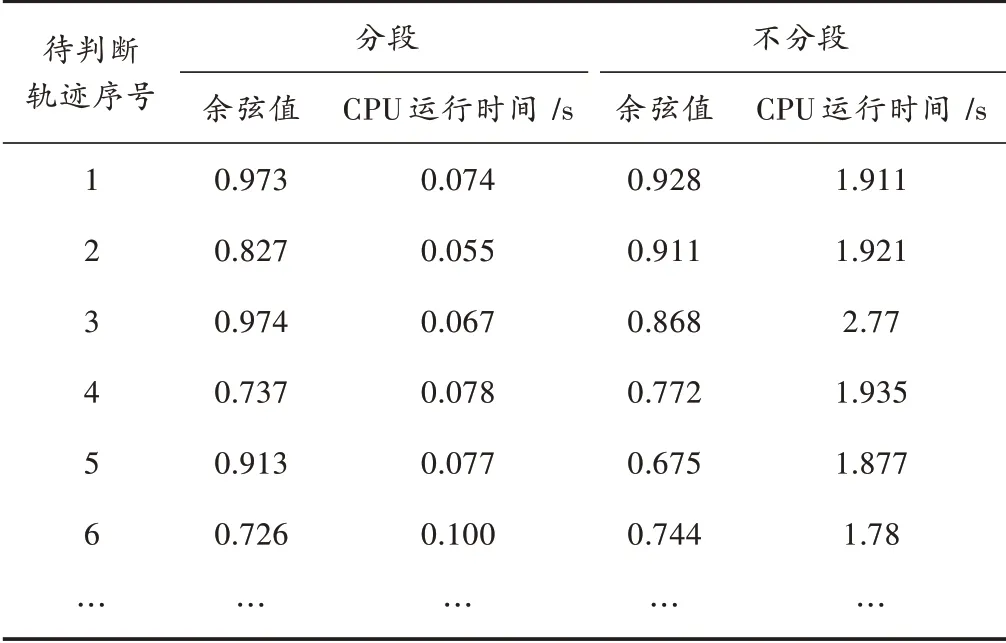
表3 10 min 间隔采样对比实验

从表3 可以看出，在对轨迹进行10 min 等间隔采样的前提下，对待判断轨迹进行相似性度量，经过分段的轨迹要比没有进行分段的轨迹CPU 运行时间平均提高了28.2 倍，原因与前面一致。

对比表2、表3 可知，在对渔船轨迹都进行分段的前提下，10 min 间隔采样比5 min 间隔采样更节省时间，CPU 运行时间平均提高了3.2 倍，在对渔船轨迹都不进行分段的前提下，10 min 间隔采样比5 min 间隔采样效率更高，CPU 运行时间平均提高了3.8 倍，原因是渔船轨迹采样间隔时间变大，轨迹采样点总数量变少，度量效率提升。

实验结果最终表明，10 min 采样间隔和分段的方式相融合可以得到较好的轨迹相似性度量结果，降低了数据计算的复杂性，提高了度量效率。

3）在对轨迹进行10 min 间隔采样前提下，对比分段以及不分段相似性度量结果的精准率以及召回率，如图6 所示。

从图6 可以看出，对于同一数据集分段以及不分段会有不同的召回率和精准率，两种度量方式精准率都较高，且两者差异较小，经过分段的轨迹精准率是88.89%，可能的原因是由于分段以后，进行相似性度量时，只要找到轨迹库里轨迹段与待判断轨迹相似性度量余弦值达到0.7 以上，便认为其为相似性轨迹，但是余弦值0.7 是人为设定的，结果会导致一定的误差。不经过分段的完整轨迹精准率为99.4%。但是不经过分段的完整轨迹召回率只有72%，可能的原因是由于待判断轨迹进行相似性度量时，轨迹库中该时间段内的轨迹存在部分轨迹缺失的现象，导致余弦值变低，所以无法准确地查找到轨迹库中所有的相似性轨迹。而经过分段的轨迹召回率为98%。实验结果表明，基于分段的余弦相似性度量在精准率和召回率上都有较满意的结果。

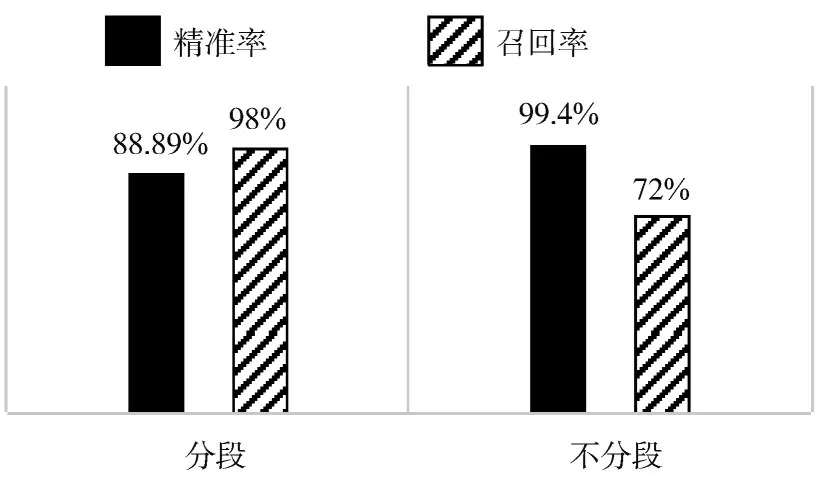
图6 精准率、召回率对比

3 结 语

为了解决“一船多码”、非法套用其他渔船的AIS 设备的问题，本文提出基于分段的渔船相似性度量方法。该方法可以更有效地找到“一船多码”的渔船，保障船舶之间的安全通信，减少水上交通事故的发生。

算法利用大连世想海洋科技有限公司提供的渔船AIS 数据，针对渔船轨迹数据的特点，对待判断轨迹和轨迹库中时间区域和待判断轨迹一样的轨迹进行了分段和不同频率的采样设置，并构建了轨迹点矩阵，对不同采样频率在分段和不分段两种情况下利用余弦相似度方法进行度量实验。通过对比分段与不分段的余弦值、CPU 运行时间、精准率和召回率，得出基于分段的余弦相似性度量在度量精度以及效率上更优异。

注：本文通讯作者为李然。