适应于WSN 的具有差错重传的轮询服务性能研究
杨志军,寇倩兰,丁洪伟
(1.云南大学 信息学院,云南 昆明 650500;2.云南省教育厅教学仪器装备中心,云南 昆明 650223)
0 引 言
无线传感器网络(Wireless Sensor Networks,WSNs)实际上就是一个分布式动态传感网络,由应用层、传输层、网络层、数据链路层和物理层五个部分组成,其中,数据链路层能够检测复用数据帧以及进行差错控制,保证点到点之间的可靠性。轮询系统作为一种排队模型,有门限、完全和限定3 种服务策略,在无线传感器网络中得到广泛应用。其中,针对减少数据冲突性、提高轮询控制系统工作效率、最小化轮询向量的长度,同时避免无用通信、降低系统延迟和系统稳定性等方面一直是研究的重点。
在对轮询系统进行改进的过程中,专家们从不同方面做了大量研究。文献[9]提出了一种新的灵活的限定服务规则,旨在最短平均队列长度和可预测的周期时间之间取得良好的平衡。由于无线传感器网络中节点的能量有限,文献[10]从无线传感器网络节能的角度出发,基于离散时间的完全服务轮询控制,提出分忙闲站点的完全服务轮询控制系统。针对轮询系统中不同优先级的业务问题,文献[11⁃12]提出区分优先级的两级轮询服务模型,实验结果表明,与普通模型相比,该模型提高了模型资源利用率和工作效率,性能大幅度提高。文献[13]提出站点休眠活动状态的限定=2 轮询控制系统,在保障系统公平性不受损害的基础上,区分站点的休眠活动状态又避免了对无信息分组的休眠站点的服务,明显改善了系统性能。但是上述文献均是在理想信道环境下进行的,缺乏对实际信道因噪声或衰减而产生差错并进行重传的研究。
在此基础上,文献[14]研究了具有重传特性的休假型排队模型和单服务器多队列轮询模型,并分析其稳态队列长度。文献[15⁃16]对轮询控制系统的重传和轮询转换周期进行研究。为了减少控制帧消耗,降低系统接入时延,文献[17]提出预约式门限服务轮询接入策略,为非理想信道环境和差错重传机制下的RoF⁃DAS WLAN网络接入性能分析提供了一种快速评估机制。本文也是对重传轮询系统进行研究,不同的是本文选择完全服务策略和限定=1 服务策略进行探究并对比其性能,具体是指在非理想信道模型中,数据包的分发存在一个出错率。在实际应用中,用户通过中央服务器轮询传输,每个用户的链路层使用自动重复请求确保数据包的无错误发送。运用嵌入式马尔科夫链和概率母函数分析方法建立数据模型,推导平均排队队长、平均轮询周期、吞吐量等系统服务性能重要指标的精确表达式。最后通过Matlab 对系统进行建模仿真和对比分析,验证系统的正确性及不同服务策略的改进效果。
1 系统工作机制
轮询控制实际上是一个防冲突协议,但在实际应用中信道环境常受噪声、自身衰减和设备误差、数据包自身错误等干扰,即存在一个数据包出错率,故本文在传统轮询服务基础上加入一个重传机制。传统完全系统服务规则具体指获得发送权的终端站需发送完当前终端站内所有数据包,直至当前终端站为空,服务器再转向下一终端站进行服务。传统限定=1 系统服务规则具体指获得发送权的终端站每次只发送站点内1 个数据包,其余数据包等待下一轮询周期和新到达的数据包以同样的服务规则进行发送。加入重传机制后,如图1所示,当数据包受到信道质量影响出错时,出错数据包都需要进行重传。即数据包再次返回源终端站并加入其缓存队列尾部,等待下一轮询周期重新进行传输,直到正确发送或重传次数达到阈值为止。若数据包的重传次数达到阈值后仍未发送成功,则当前终端站丢弃该数据包,放弃重传。
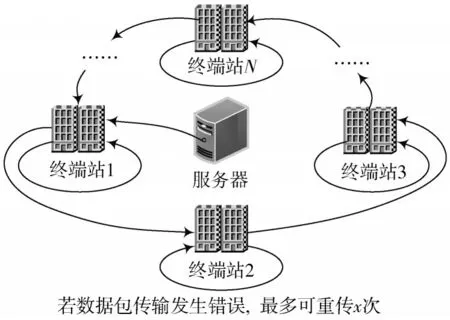
图1 数据分发结构图
2 模型研究
在实际通信环境中,数据包传输的信道为非理想信道。系统在下列条件下展开工作:
1)到达各终端站存储器内的数据包均服从泊松分布,且相互之间保持独立,其概率母函数为(),均值为=′(1),方差为=″(1)+-。
2)任意终端站在接受服务时成功发送一个数据包的时间独立同分布,其概率母函数为(),均值为=′(1),方差为=″(1)+-。
3)服务器在任意两个逻辑上相邻的终端站之间的查询转换时间独立同分布,其概率母函数为(),均值为=′(1),方差为=″(1)+-。
4)各个终端站存储器的容量巨大,不会发生信息分组丢失。
5)数据包在终端站存储器内按照先进先出(First Come First Service,FCFS)的规则进行发送。
6)本文是在对称轮询系统基础上进行研究的,故系统达到稳定工作状态的条件为:<1。
给出定义(,=1,2,…,)如下:
1)非理想信道下的数据包错误率,即重传概率为p;
2)重传阈值为,出错数据包最多可以重传次,若次后仍失败,则放弃重传,丢弃出错数据包;
3)服务器从号终端站转向+1 号终端站的查询转换时间为u();
4)服务器对号终端站内的数据包进行服务的时间为υ();
5)数据包在u()时间内进入号终端站的数量为μ(u);
6)数据包在υ()时间内进入号终端站的数量为η(υ)。
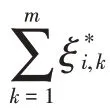

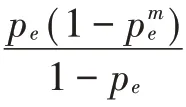
在t时刻,+1 号终端站接受服务器的服务,此时其终端站存储器内的数据包数量为ξ()。故整个排队系统在t时刻队列长度的状态变量为{(),(),…,ξ(),…,ξ()},其概率分布为[ξ()= x;=1,2,…,],故个系统状态变量的概率分布函数为π(,,…,x,…,x),即:
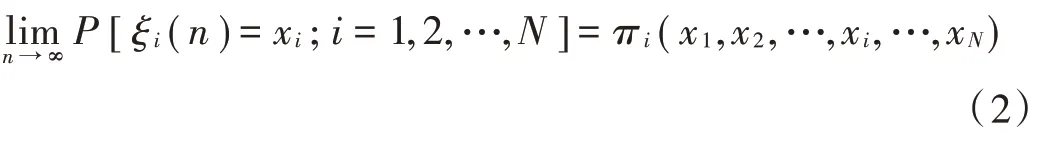
定义π(,,…,x,…,x)的概率母函数为:
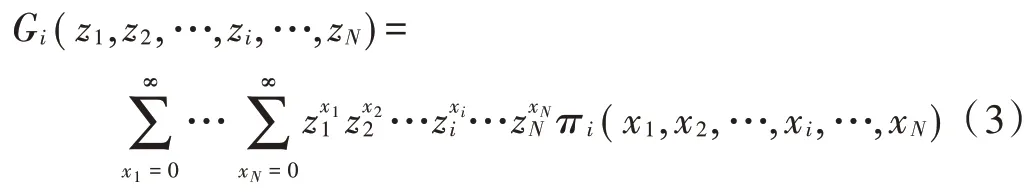
将式(2)代入式(3)得:
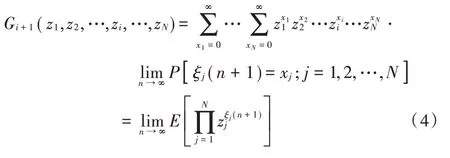
2.1 重传限定K =1 数学模型
由以上描述可知,重传限定系统各个时刻状态变量满足下列关系式:

将式(5)代入式(4),并由式(1)化简得:
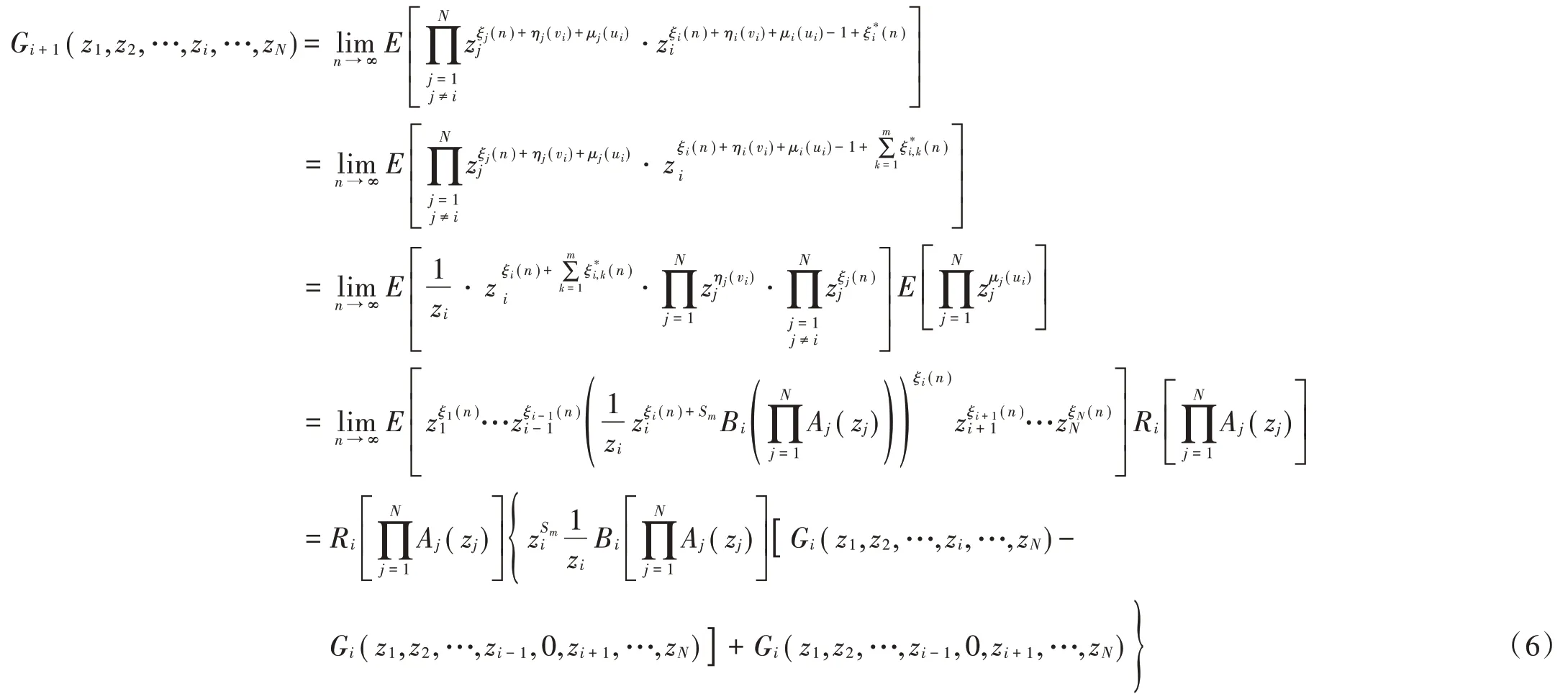
定义第号终端站在t时刻接受服务,此时号终端站内存储的数据包数量为g(),且:
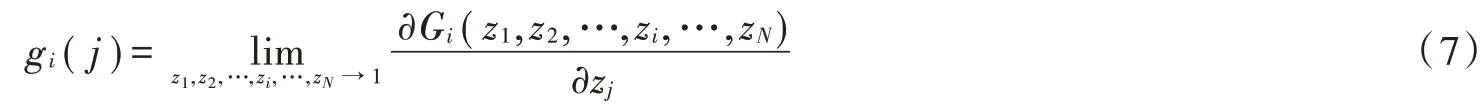
定义:

故:
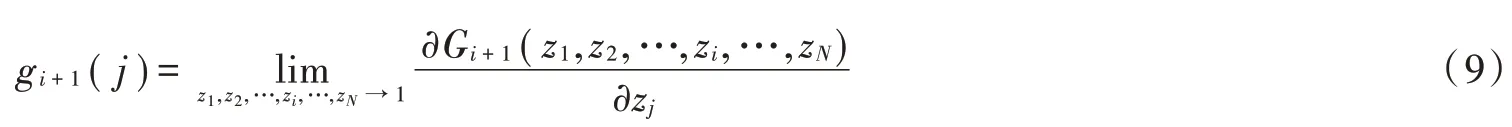
由式(9)得:
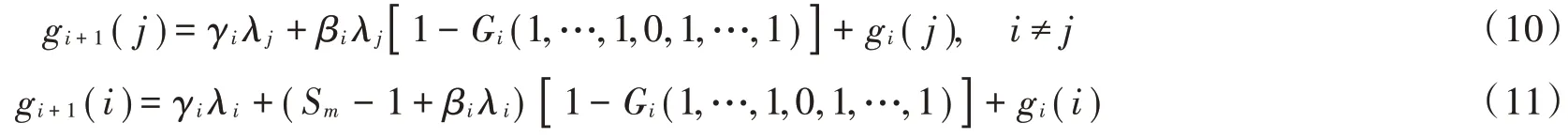
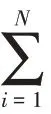
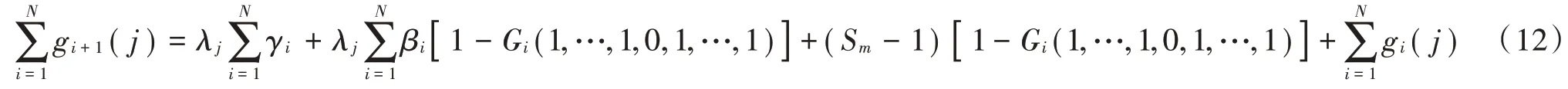
化简得:
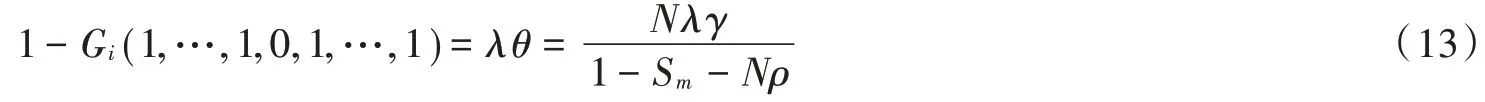

2.1.1 平均排队队长
平均排队队长指等待发送的数据包在终端站存储器内的排队长度。
定义:
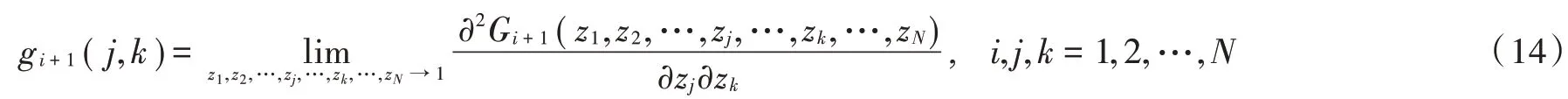
由式(14)得:
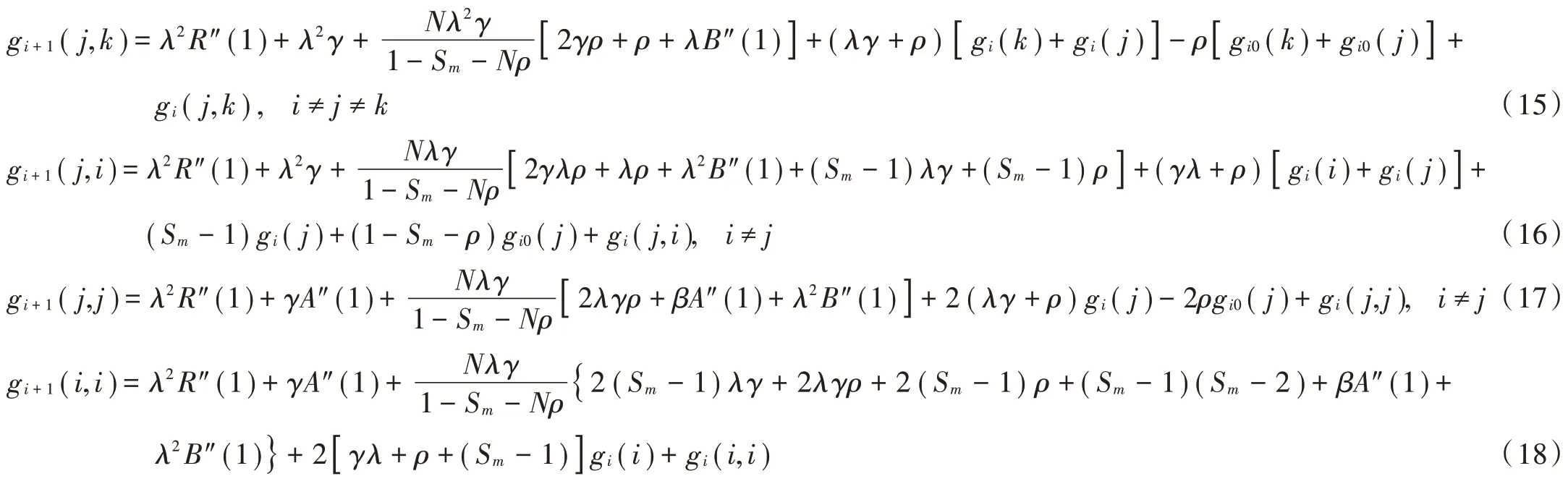


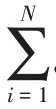
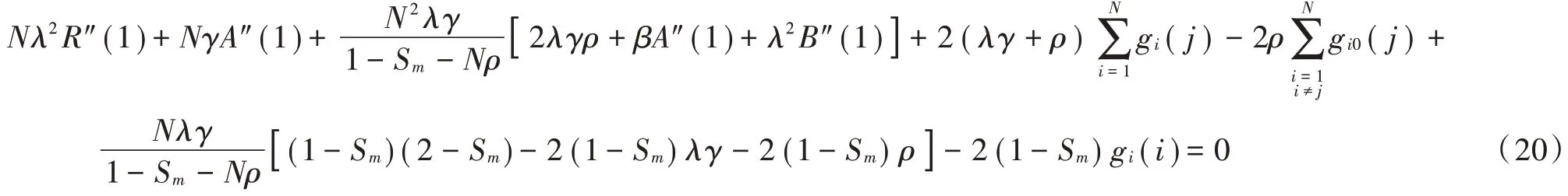
将式(20)代入式(19)并化简得到重传限定=1 服务系统的平均排队队长为:

2.1.2 平均轮询周期
平均轮询周期指服务器连续两次查询同一个站点所需要的时间。由式(13)得到重传限定=1 服务系统的平均轮询周期为:

2.2 重传完全数学模型
由文献[20]可知,在任一时段内,服务器对任意一个终端站内到达的数据包以及在服务期间到达的数据包使用完全服务方式所需时间都服从一个相互独立且同分布的概率分布,其概率母函数为:

对式(23)求一阶导,得:

对式(24)求二阶导,得:

重传完全系统各个时刻状态变量满足下列关系式:

将式(26)代入式(4),并由式(1)化简得:

2.2.1 平均排队队长
由式(9)得:
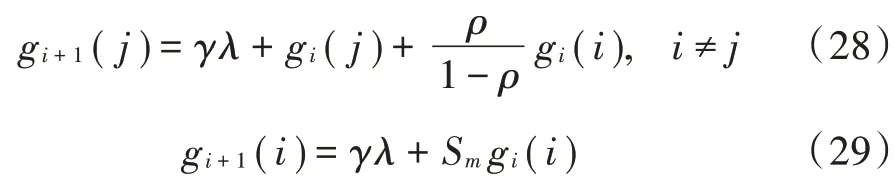

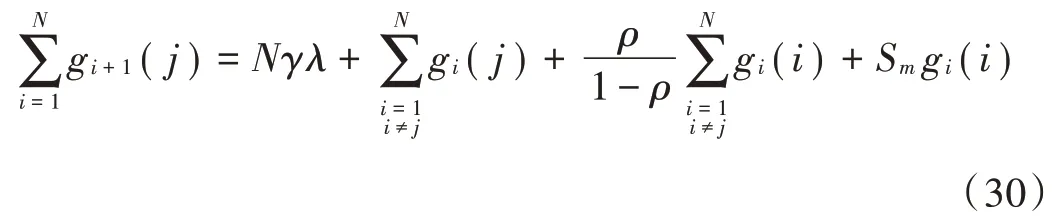
化简后得到重传完全的平均排队队长为:
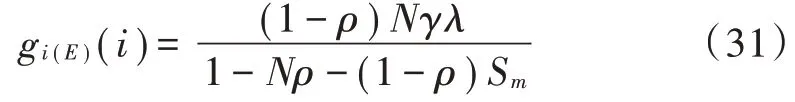
2.2.2 平均轮询周期
借用文献[21]方法,推导得出重传完全的平均轮询周期为:
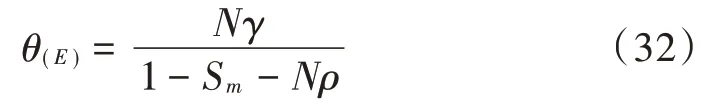
2.3 吞吐量
系统吞吐量指单位时间内系统所能传输的数据包的个数:

3 性能分析
根据以上理论分析结果,本文对重传轮询系统在Matlab 平台上进行仿真。为验证理论分析模型的正确性,本文将理论值与仿真值进行对比。此外,还具体针对重传次数和重传概率对系统平均排队队长、平均轮询周期和吞吐量的影响展开研究。
假设重传轮询系统中有5 个终端站,服务器在相邻站点间查询转换率为1 时隙,对各个站点的服务率为2 时隙/数据包,重传阈值为1,重传概率为0.1。在此条件下进行仿真,结果如图2~图7 所示。
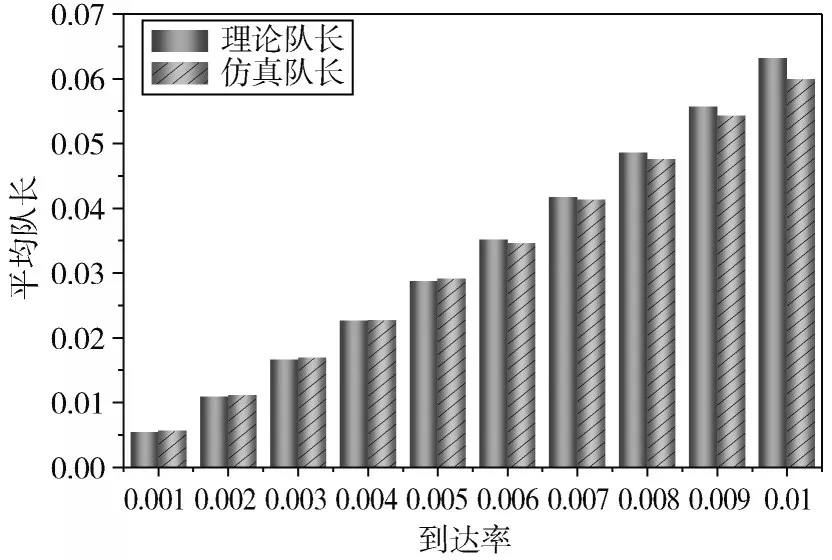
图2 重传限定K =1 服务平均排队队长
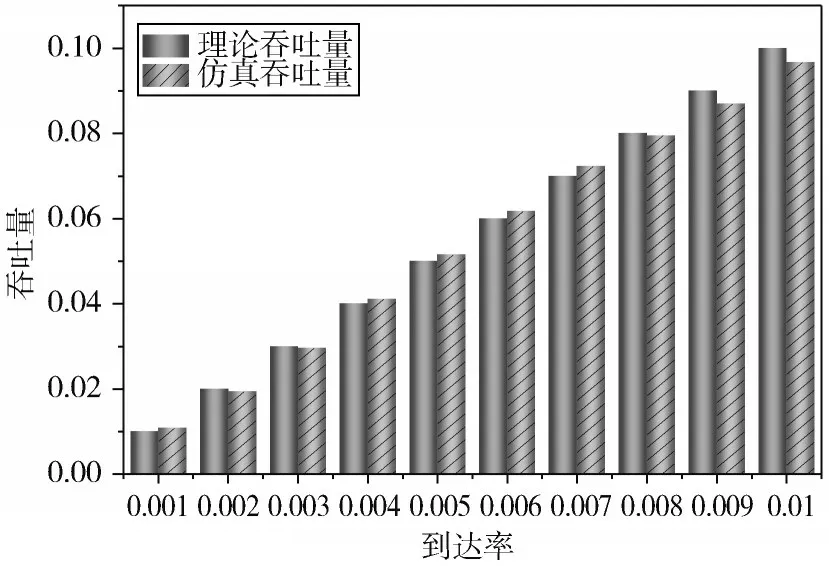
图7 重传完全服务吞吐量
由图2~图4 可知,重传限定=1 的平均排队队长、吞吐量随到达率的增加而不断增加,与实际相符。由于平均轮询周期只与服务时间和查询转换时间有关,故平均周期随到达率的变化保持一个相对稳定的状态,与实际相符,且平均排队队长、平均轮询周期和吞吐量的理论值和仿真值误差较小,故证明了重传限定=1 的理论分析的正确性。
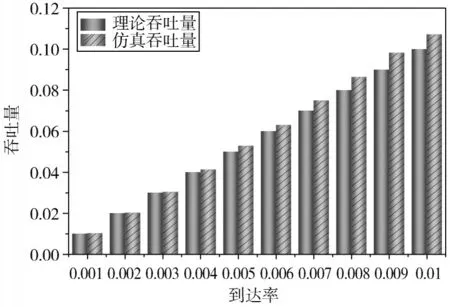
图4 重传限定K =1 服务吞吐量
由图5~图7 可知,重传完全的平均队长和吞吐量随到达率递增,平均周期保持相对稳定,与实际相符,且平均队长、平均周期和吞吐量的理论值与仿真值大致相等,验证了理论分析的正确性。由式(22)、式(32)、式(33)可知,在同一条件下,重传完全和重传限定=1 系统各自的平均周期和吞吐量的理论值是相等的。对比图3和图6、图4 和图7,可以看出重传完全的理论值和仿真值的误差略小于重传限定=1,仿真效果更好。对比图2 和图5,明显看出重传完全平均队长的理论值和仿真值的误差也略小于重传限定=1。再次说明重传完全的仿真效果更好,但两者差距不大。以下将针对这两个系统做更加细致的研究。
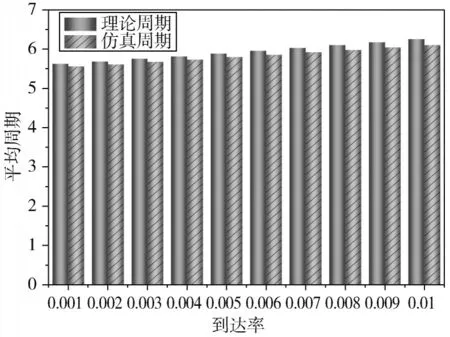
图3 重传限定K =1 服务平均轮询周期
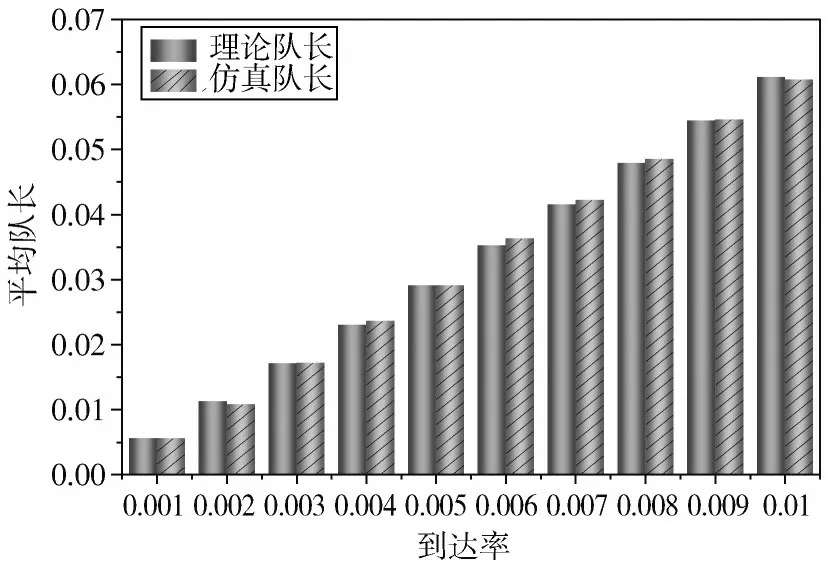
图5 重传完全服务平均排队队长

图6 重传完全服务平均轮询周期
在上述查询转换率、服务率和终端站个数的基础上,将传统限定和完全模型与重传限定和完全模型进行对比,如图8 所示。在相同吞吐量条件下,重传轮询系统的平均队长略高于传统轮询,这是因为在非理想信道中,部分数据包出错需要进行重传,直到成功发送或超过重传阈值被丢弃。故数据包在终端站的排队长度比理想信道更长。对于传统轮询系统,当到达率小于0.004 时,限定=1 和完全服务的平均队长几乎相等;当到达率大于0.004 时,限定=1 的平均队长略大于完全服务。加入重传机制后,当到达率小于0.007 时,重传限定=1 和重传完全服务的平均队长几乎相当;当到达率大于0.007 时,重传限定=1 的平均队长逐渐大于完全服务。由此看出加入重传机制后,并没有对限定=1 服务和完全服务平均队长的整体趋势产生明显的影响。当到达率较小时,重传限定=1 服务的平均排队队长与重传完全大致相等。
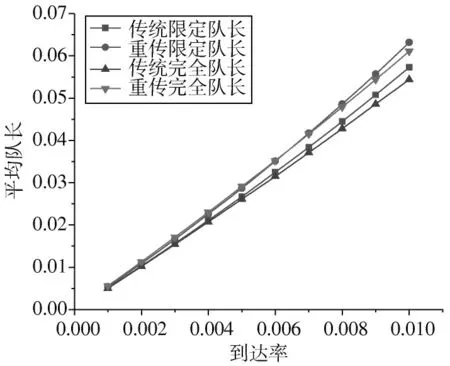
图8 平均队长对比
同样地,在以上实验条件下,对比重传概率为0.01,0.1,0.15,0.2 时系统的平均队长。由图9、图10 可知,基于相同负载,重传概率越大,系统的平均队长也相应增加。随到达率增加,不同重传概率的平均队长之间的差距越明显,且针对不同重传概率的平均队长,重传限定=1 各队长之间的差距小于重传完全服务。故重传限定=1 的系统性能受重传概率变化的影响较小,对比重传完全服务其系统性能更加稳定。

图9 重传限定K =1 服务平均队长与重传概率的关系

图10 重传完全服务平均队长与重传概率的关系
设定系统终端站为5 个,到达率为0.005 数据包/时隙,服务率为2 时隙/数据包,查询转换率为1 时隙。取重传阈值从1~10 以1 为步长依次递增,对比重传概率为0.01,0.1,0.15,0.2 时系统平均排队队长的变化。由图11、图12 可知,在非理想信道环境下,基于相同负载重传阈值对系统平均队长的影响随重传概率的增大而增大。当p=0.01 时,重传次数的变化不会对平均队长产生影响,队长收敛于一个特定的数。当p=0.1 和p= 0.15 时,若≤3,系统平均排队队长随的增大而逐渐增大;若>3,系统平均排队队长收敛于一个特定的数。当p=0.2 时,若≤4,系统平均排队队长随增大而增大;若>4,系统平均排队队长收敛于一个特定的值,且重传概率越大,平均队长收敛的特定值越大。由此可见,系统平均队长受重传概率影响较大,当重传概率确定时,系统平均排队队长可收敛于一个特定的值,不再受重传次数的影响。
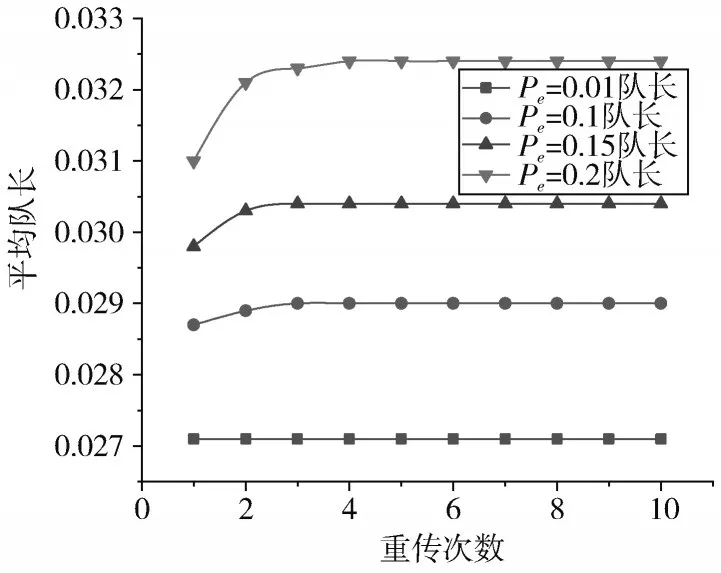
图11 重传限定K=1 服务平均队长与重传次数的关系
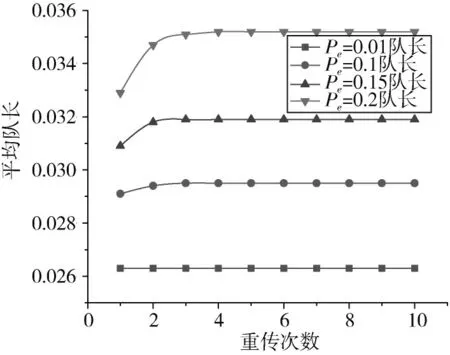
图12 重传完全服务平均队长与重传次数的关系
综上所述,重传完全和重传限定=1 服务的吞吐量及轮询周期相同。基于相同负载,重传完全系统的平均队长小于重传限定=1 系统,故信息处理效率更高。重传概率即数据包出错率,对系统性能影响较大,换言之,信道质量越好,数据处理效率越高,反之,效率越低。信道质量一定时,系统性能也趋于稳定。
4 结 语
本文研究了非理想信道环境下,在传统轮询系统中加入重传机制,即出错数据包需返回源终端站,等待下一次重新发送,直到发送成功或重传次数超过阈值该数据包被抛弃。具体研究了重传限定=1 和重传完全两种服务策略。运用嵌入式马尔科夫链和概率母函数方法对这两种模型进行数学分析和理论推导,得出系统平均排队队长、平均轮询周期和吞吐量的理论表达式,并在Matlab平台对系统进行仿真。结果证明系统的理论值和仿真值误差较小,验证了理论分析的正确性。本文将非理想信道下的重传模型与理想信道下的传统轮询模型进行对比,结果发现,重传模型的平均排队队长略高于传统服务方式,与实际相符,再次验证了其理论分析的正确性。最后,通过在不同重传概率和重传次数下系统性能的对比,得出重传概率对系统性能的影响较大,重传次数对系统性能的影响较小。未来工作中,本文将进一步在降低重传概率、提高信息传输效率方面展开研究。

