基于FFT 变换和ADALINE 网络的实时音频滤除窄带噪声方法

谢家兴，梁高天，尹东晓

（1.华南农业大学 电子工程学院，广东 广州 510642；2.广东省智慧果园科技创新中心，广东 广州 510642；3.广东省农情信息监测工程技术研究中心，广东 广州 510642；4.罗定职业技术学院，广东 云浮 527200）

0 引 言

高斯窄带噪声是指概率密度函数满足正态分布统计特性、功率谱密度函数是常数且频带宽度远远小于其中心频率的一类噪声。在音频信号的调制、传输、解调中，往往会引入很多高斯窄带噪声，严重时会非常刺耳，影响音频收听者的收听体验。

传统的高斯窄带噪声滤波有谱减法，该方法首先对音频信号进行FFT 变换，在频域移除音频信号中的噪声频谱成分后，再通过IFFT 变换得到滤波结果。尽管该算法可以有效提升信号的信噪比，但该方法需要做两次FFT 变换，大大增加了处理时延，使得算法的实时性得不到保证。

另一种传统方法是小波变化法，该方法首先对电子音乐信号进行鲁棒主成分分析，通过分析检测电子音乐信号中具体噪声位置，将电子音乐信号与噪声信号进行有效分离，再对经过鲁棒主成分分析后的电子音乐信号通过改进傅里叶变换算法进行有效降噪处理。该方法虽然滤波效果好，但是滤波流程复杂，有较多的参数需要人为调整，为算法的使用带来诸多不便。

本文提出基于FFT 变换和ADALINE 网络的实时音频滤除窄带噪声方法，该方法首先通过FFT 变换获得噪声频率，通过噪声频率重构噪声样本，根据噪声样本利用改进ADALINE 网络再现加入到音频信号中的高斯窄带噪声，将噪声信号减去再现的高斯窄带噪声从而实时地实现音频去噪。

1 系统基本结构

1.1 自适应ADALINE 网络

自适应ADALINE 网络在ADALINE 网络的基础上，引入抽头延迟线，该网络结构如图1 所示。

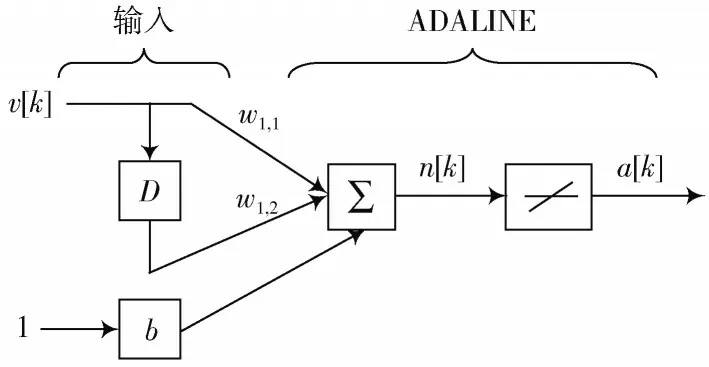
图1 自适应ADALINE 网络结构图

该网络由1 个一阶抽头延迟线和1 个ADALINE 网络组成，网络的输出可由式（1）计算：

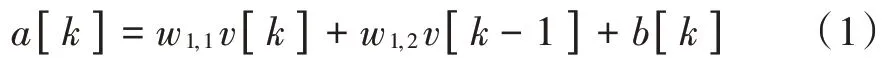
式中：为网络输出；[]表示网络本次输入；[-1]表示网络上一次输入；表示偏置。

1.2 噪声消除系统

噪声消除系统的原理如图2 所示，音频信号在传输时，因被加入多个高斯窄带噪声而成为噪声信号，把噪声信号输入到噪声成分分析器，噪声成分分析器基于快速傅里叶变换，给出初步的高斯窄带噪声频率，并通过频率重构噪声。自适应滤波器由自适应ADALINE 网络组成，它的输出可以“模拟”之前加到音频信号上的多个高斯窄带噪声，通过相减器，噪声信号减去重现的噪声即可得到音频信号。同时，把滤波结果作为误差反馈到自适应滤波器作为学习数据，从而实现自适应滤波。

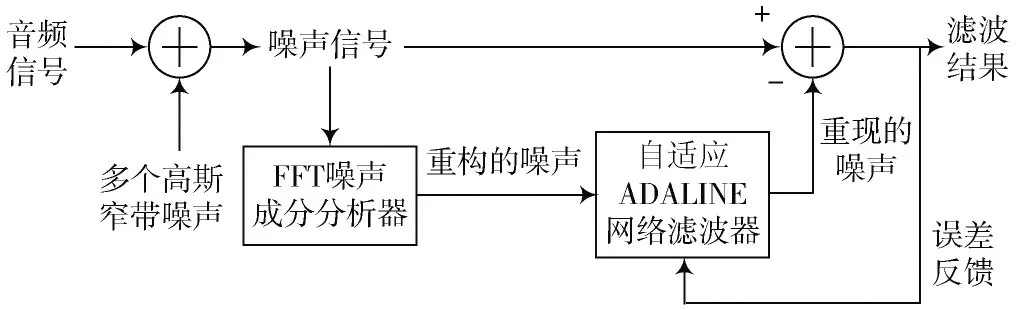
图2 噪声消除系统原理图

1.3 自适应滤波器

1.3.1 单窄带噪声

当噪声信号中只有一个高斯窄带噪声时，可用图2所示的自适应ADALINE 网络作为自适应滤波器。重构的噪声信号为：

式中，ω表示高斯窄带噪声的中心频率，该频率由噪声成分分析器给出。

将式（2）得到的重构噪声信号利用抽头延迟线进行一阶延迟，如式（3）所示。

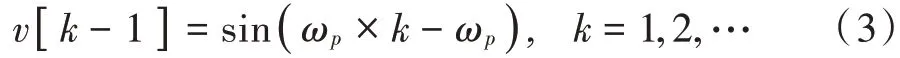
由式（3）可知，延迟一拍即是对信号进行一次相移，相移量为信号的角频率。引入单高斯窄带噪声的噪声信号为：

式中：[]表示音频信号序列；[]表示噪声信号；[]表示引入的单个高斯窄带噪声；与未知，分别表示窄带噪声的频率与相位。通过FFT 噪声成分分析可以得到近似于的ω，根据三角函数的定义，有：

式中，[]表示重现的噪声，噪声信号减去重现的噪声后，即可恢复出原来的音频信号，即：

自适应ADALINE 网络目标是找到合适的与使式（5）成立。因为输入到网络中的信号只有一个频率成分，并且网络是一个线性系统，所以网络的输出为输入的正弦波的增减幅和变相，输出的频率与输入保持一致。因此，噪声信号减去重现的噪声后，噪声信号被滤除的是信号中的某个频率成分，其他频率成分不会因此而改变，所以该方法可以有效去除噪声信号中的高斯窄带噪声。

1.3.2 多高斯窄带噪声

改进的自适应ADALINE 网络如图3 所示。

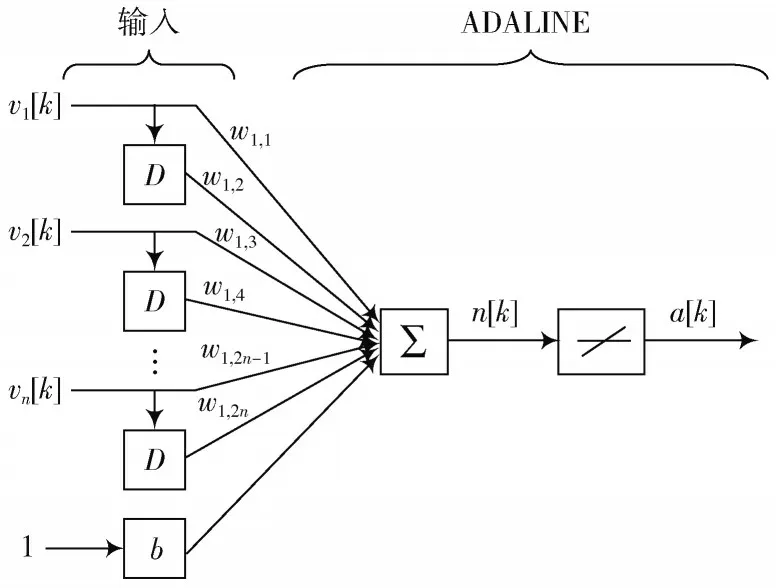
图3 改进的自适应ADALINE 网络

图3 中的()表示噪声样本，由FFT 噪声成分分析器提供，用式（7）表示：

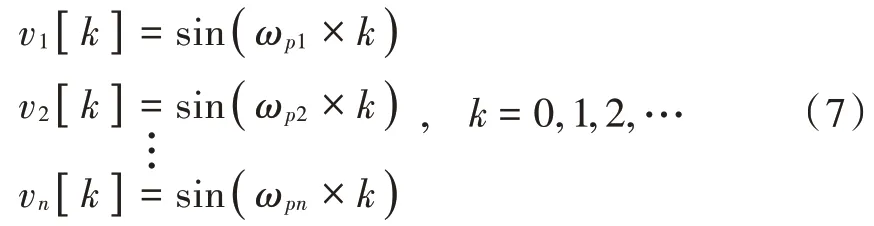
式中：噪声数量由人为设定；角频率ω由FFT 噪声成分分析器给出，与单窄带噪声时类似，多窄带噪声自适应滤波器只能输出与输入一样的频率信号的叠加，把噪声信号减去自适应滤波器的输出作为滤波结果，同时把滤波结果反馈到自适应滤波器用于权值更新，网络训练采用Widrow⁃Hoff 方法，该方法在尝试最小化误差反馈的过程中实现滤波去噪。权值与偏置值的更新如式（8）所示：

式中：表示学习率；为噪声信号中窄带干扰的数量；表示误差反馈信号。初始的权值以及偏置值由系统随机生成。

1.4 噪声成分分析器

噪声成分分析器基于FFT 算法提取噪声信号中窄带噪声的频率，同时根据噪声的频率重构噪声样本，把样本提供给自适应ADALINE 网络滤波器用于去噪。

1.4.1 快速傅里叶变换（FFT）

快速傅里叶变换是一种对信号做离散傅里叶变换的方法，离散傅里叶变换的定义如式（9）所示。

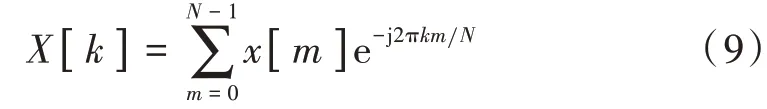
式中：为一组时域的信号序列；表示时域序列的长度（即序列有个样点）；e 为自然常数；j 表示单位虚数；为离散傅里叶变换后的频域序列。通过离散傅里叶变换可以获得信号的频率成分，进而分析出信号的噪声频率，提供给自适应滤波器。

1.4.2 工作原理

因为在音频信号中，窄带噪声在频谱上的幅度一般要高于原信号，只要在频谱上找出个最大的幅度对应的频率，把频率传给自适应滤波器，即可去除窄带噪声。其中是人为设置的窄带噪声数量，如果设置的噪声数量比实际要小，滤波后仍会残留噪声；如果偏大，因为音频信号频谱非常密集，对于音质并不会有太大影响。

2 仿真分析

2.1 噪声信号

仿真使用了一段音乐作为音频信号样本，在信号中加入了5 个振幅为0.1 的正弦波模拟高斯窄带干扰，这些信号的频率以及对应的相位如表1 所示。音乐信号加入噪声前的频谱如图4 所示，加入噪声后的频谱如图5 所示。

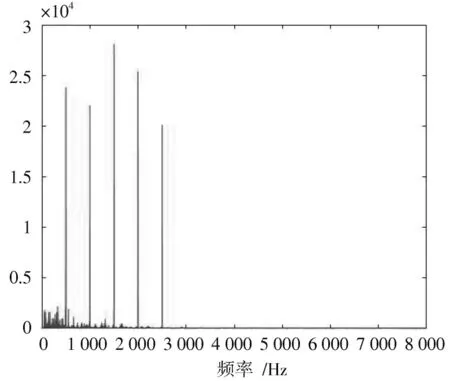
图5 加噪后频谱

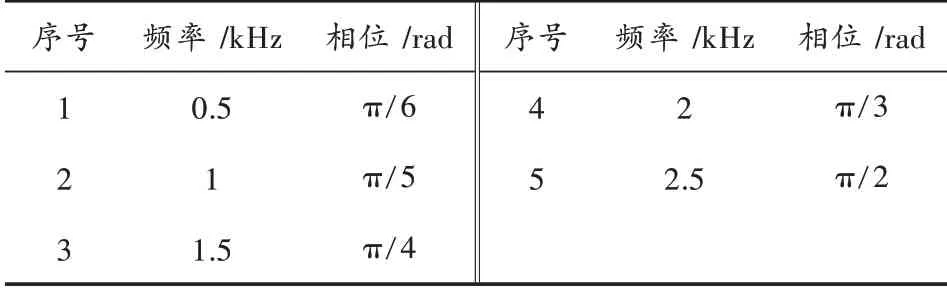
表1 仿真时加入到音频信号中的噪声频率与相位

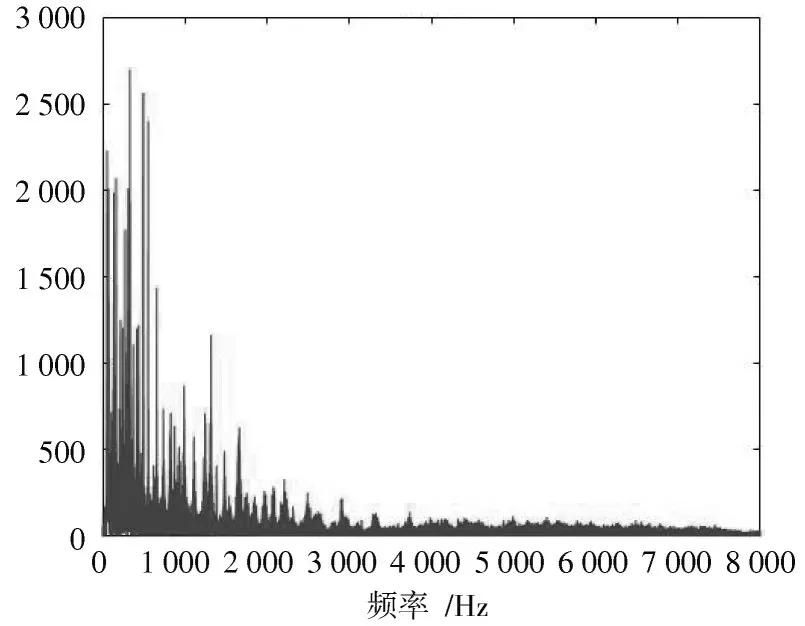
图4 原信号频谱

2.2 噪声成分分析器

人为地设置噪声数量=6 个（注意比2.1 节加入的噪声数量多了1 个）。噪声成分分析器测量出6 个噪声频率，这6 个频率及其与真实值的误差如表2 所示。误差计算公式为：

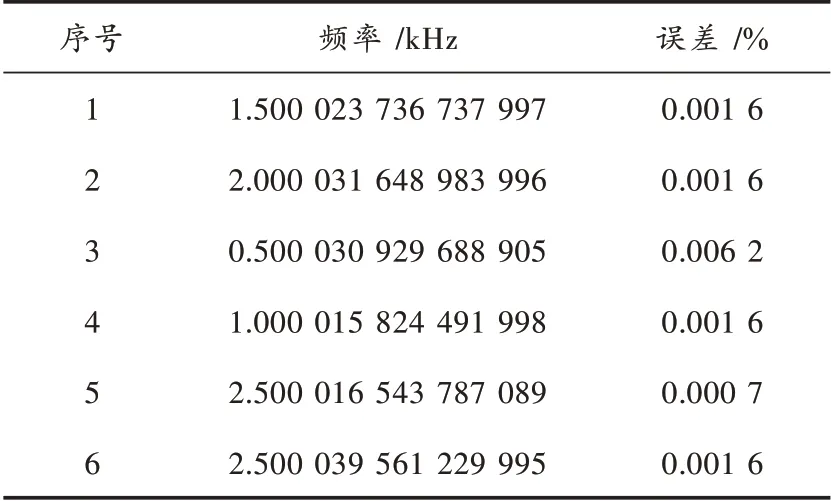
表2 设置6 个噪声时，噪声成分分析结果及其误差

在分析出噪声信号的频率后，分析器根据预测频率分别构建与噪声等频率初相位为0 的个正弦波，是人为设置的窄带噪声数量，把这些正弦波作为噪声样本输入到自适应滤波器实现去噪。

2.3 自适应滤波器

把噪声样本输入到自适应ADALINE 网络滤波器，网络的权值与偏置在滤波时不断地更新。图6 所示的是音频时域图，取前1 000 个点进行展示。

由图6 滤波后曲线可以看到，一开始网络根据随机初始化的权值输出的滤波结果非常大，随着滤波的进行，网络在不断地更新权值，最终迭代到稳定点，所以在音频的开始会有很大的噪声，随着时间的推移，噪声逐渐减少，到最后几乎没有噪声。

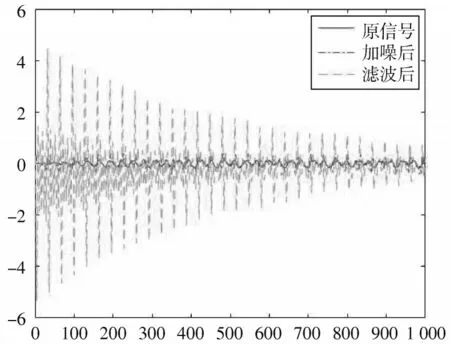
图6 音频时域图（前1 000 个点）

滤波后的频谱图如图7 所示。

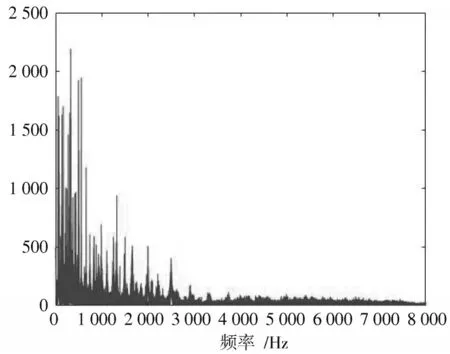
图7 滤波后频谱

与原信号频谱（图4）比较可以发现，滤波后的频谱与原信号的频谱基本相似；再与加噪后的频谱（图5）比较，发现滤波器很好地滤掉了加入到音频信号中的窄带噪声。

2.4 滤波效果

均方根误差是衡量滤波效果的一个指标，计算公式为：

式中：RMSE 表示均方根误差；in[]表示精确值序列；out[]表示需要计算与精确值序列的均方根误差的序列。

信噪比是衡量信号失真程度的一种方法，可以使用式（12）计算：

式中和分别代表信号和噪声电压的“有效值”。为了应用到本例的计算中，对这个公式进行改进，改进后的表达式为：

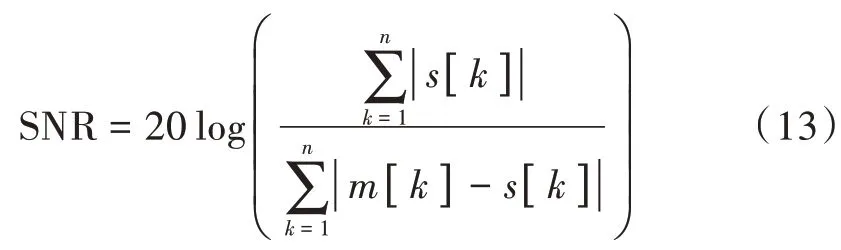
式中：[]表示原音频信号；[]表示要计算信噪比的信号。

噪声平均抑制比可用于衡量滤波算法对于噪声的抑制程度，通过式（14）计算。

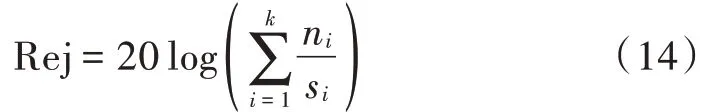
式中：Rej 表示噪声平均抑制比；为噪声数量；和表示滤波前后窄带噪声对应频率的频谱强度。

滤波性能比较结果如表3 所示。

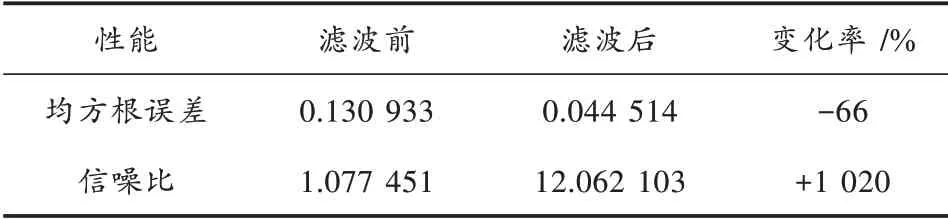
表3 滤波性能结果

计算可得本文算法的噪声平均抑制比为32.325 2 dB。

从结果可以看出，本文的自适应滤波器对于被多个高斯窄带噪声干扰的音频信号有很好的过滤效果，特别是对于被强高斯窄带噪声污染的信号，本算法可以让原信号的信噪比提高11 dB。

2.5 滤波耗时

本节通过对一采样率为16 kHz、采样点数为695 125的音乐进行滤波，并测量其耗时。

经过5 次测量，计算出平均耗时以及耗时标准差，结果如表4 所示。

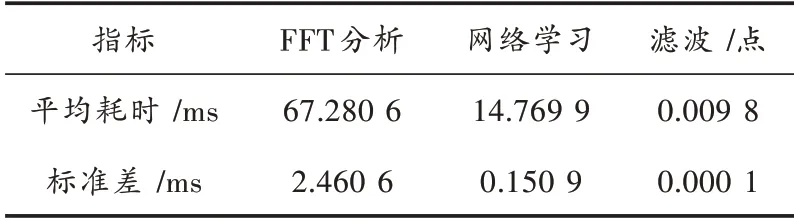
表4 测量结果

在噪声信号中的噪声频率发生改变后需要重新初始化网络，网络的初始化时间等于FFT 分析时间加上网络学习时间，由测量结果可以算出，初始化耗时平均为82.050 5 ms。在网络初始化后，平均每9.8 μs输出一个样点，也就是说训练后网络的最高处理速度约为102 kHz，这个处理速度足以实时处理当前的音频信号。

3 结 语

本文提出了一种基于FFT 变换和ADALINE 网络的实时音频滤除窄带噪声方法，该方法通过FFT 获取噪声的频率，利用噪声频率重构噪声，并把重构的噪声输入到改进自适应ADALINE 网络滤波器，滤波器通过反馈信号进行学习，在学习的过程中使重现的噪声越来越逼近音频信号引入的窄带干扰，使用相减器把噪声信号减去重现的噪声，从而恢复原音频信号。

仿真结果表明，噪声成分分析器可以准确得到噪声频率，噪声信号通过本文方法滤波，信号的均方根误差（RMSE）减少了66%，信噪比（SNR）增加了11 dB，噪声平均抑制比达到32 dB，因此音频质量得到了显著提高。另一方面，本文算法只需要大约82 ms 即可完成初始化，同时训练后网络的最高处理速度高达102 kHz，说明本文算法可以应用于实时的音频处理系统中。

注：本文通讯作者为尹东晓。