基于网格搜索超参数优化的支持向量回归

刘佳星

（齐齐哈尔大学，黑龙江 齐齐哈尔 161006）

1 概述

支持向量机(SVM)是一种监督学习的数据挖掘模型，其主要目标是找到一个使类之间距离最大化的超平面[1-2]。支持向量机分为支持向量分类机和支持向量回归机。支持向量分类机（SVC)用于研究输入变量与二分类型输出变量的关系预测；支持向量回归机（SVR)用于研究输入变量与数值型输出变量的关系,对新观测的输出变量值进行预测。

SVM基于统计学习理论，在解决非线性、小样本和高维的回归和分类问题上有许多优势。正因如此，SVR 已经成功应用与诸多领域，例如：工业建筑[3-7]、生物医疗[8-9]、地理环境[10-11]、农业金融[12-13]和物理化学[14-17]。

2 支持向量回归

如图1 所示是有两个输入变量情况下的支持向量回归超平面。

图1 支持向量回归超平面

为了降低过拟合风险，采用ε- 不敏感损失函数，ε（ε＞0）是观测X 输出变量的实际值与预测值之间允许的最大偏差。“管道”内的ε 很重要，ε 过大或过小都会影响预测结果（见图2）。所以，需要权衡过拟合风险和预测偏差。一方面通过适当增加“管道”内的ε，尽量降低过拟合风险，另一方面损失函数值也不能过高。

图2 ε- 管

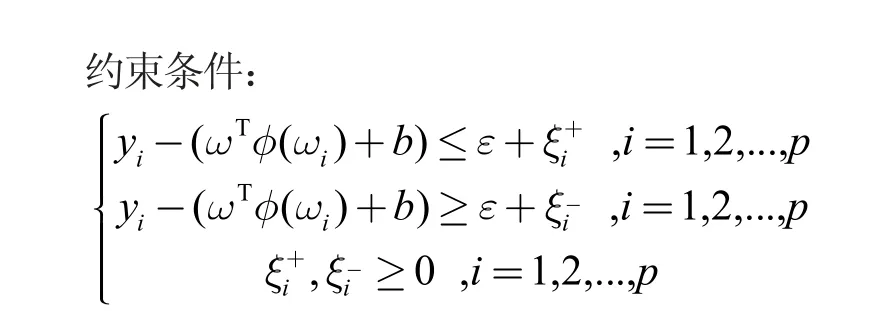
目标函数中的可调参数C（Cost＞0）是损失惩罚函数，用于平衡模型复杂度和损失。C较大时，将导致“管”过窄；C较小或趋近于0 时，将导致“管“过宽。参数C太大或太小都不恰当，可通过N折交叉验证方式确定参数C。

支持向量机具有如下优点：（1）SVM训练相对容易。与神经网络不同，没有局部最优。（2）SVM有正则化参数，可以帮助避免过度拟合。（3）在高维空间中依然有效。（4）在决策函数中使用训练点的子集（称为支持向量，见图2 右图），因此它也具有内存效率。尽管如此，SVM也存在求解模型的参数难以解释、SVR 的超参数对模型精度有显著影响这一不足。

3 超参数优化

在机器学习中，超参数优化旨在寻找使得机器学习算法在验证数据集上表现性能最佳的超参数，这些超参数返回一个优化模型，该模型减少了预定义的损失函数，进而提高了给定独立数据的预测或者分类精度。那么如何优化超参数至关重要。

为了进行超参数调优，我们一般会采用网格搜索、随机搜索和贝叶斯优化等算法[20]。随机搜索要求样本点集足够大，贝叶斯优化算法又容易陷入局部最优值。网格搜索是最应用最广泛的超参数搜索算法，通过查找搜索范围内的所有的点来确定最优值。如果采用较大的搜索范围以及较小的步长，网恪搜索大概率找到全局最优值。

4 衡量标准

本研究通过计算平均绝对误差(Mean Absolute Error，MAE)、均方误差(Mean Square Error，MSE)和均方根误差(Root Mean Square Error，RMSE) 来测试回归器的准确性。三种衡量标准的计算公式如下：

假设，预测值：y^={y^1，y^2，y^3，…，y^n}，真实值：y={y1，y2，y3，…，yn}，

其中n 是预测数据长度。四种评估指标均用于测量观察值与真实值之间的偏差，同时也是机器学习模型预测准确性的度量标准。他们的值越大，代表模型的性能越低，预测值和真实值之间的偏差也越大。

5 实验

本研究在R 语言（64 位）平台上进行，首先将线性回归（lm）、SVR 和超参数优化的支持向量回归三种回归器建模，然后通过三种评价指标，分析三个模型的准确性。

实验第一步创建线性回归模型并将其可视化，如图3所示：实心圆表示输入变量X 的真实值，直线为其线性拟合。此时线性回归的均方根误差为5.719515，平均绝对误差为4.758571，均方误差为32.71286。从评价指标和图3 中都看出lm的准确性较差，有效性不佳。

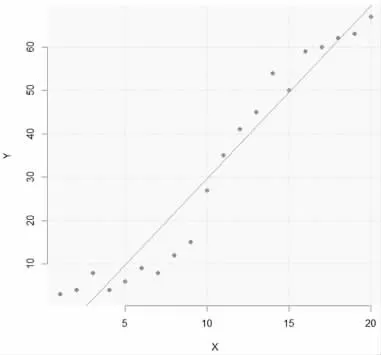
图3 观测值与线性回归

实验第二步在R 平台上调用e1071 包创建支持向量回归模型，如图4 所示：×表示输出的预测值。此时SVR 的均方根误差是3.003165，平均绝对误差是2.529023，均方误差是9.019002。SVR 的衡量指标相较于lm均有显著提高。

图4 观测值与支持向量回归

为了提高支持向量回归的性能，我们将采用网格搜索方法进行超参数优化，为模型选择最佳参数C 和ε。实验第三步调用tune( )函数，并绘制网格搜索结果。在图5 中可以观察到，区域颜色越深，模型性能就越好（因为RMSE 在深色区域更接近于零）。实验第四步将在更窄的范围内尝试另一个网格搜索，尝试在0 和0.2 之间的寻找ε 值。

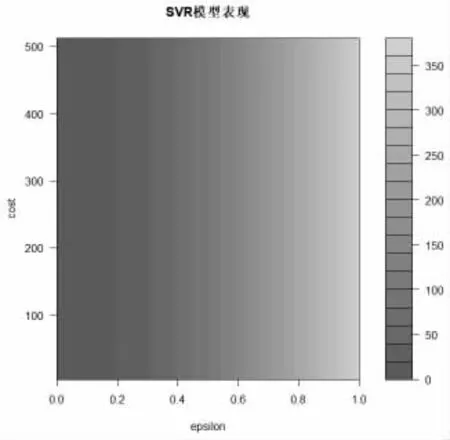
图5 SVRcost 与ε

最终通过网格搜索获得SVR 的最佳参数：cost=128，ε=0.09。（图6）

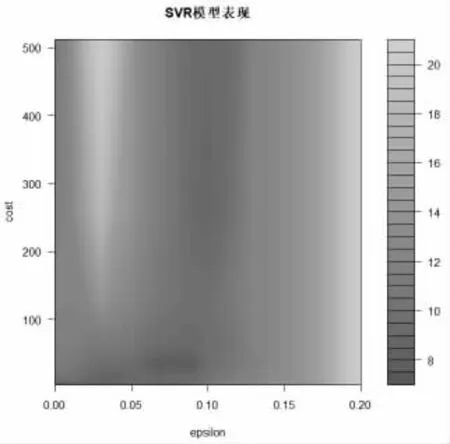
图6 优化的SVRcost 与ε

超参数优化SVR 的均方根误差是1.931165，平均绝对误差降低到1.632323，均方误差为3.729399，三种评价指标均获得最低值（见图7）。

图7 三种评价指标柱状对比图

实验第五步将SVR 和超参数优化的SVR 这两个模型可视化。在图8 中，细线条表示默认参数的SVR，粗线条表示超参数调优后的SVR 模型，拟合效果最佳。

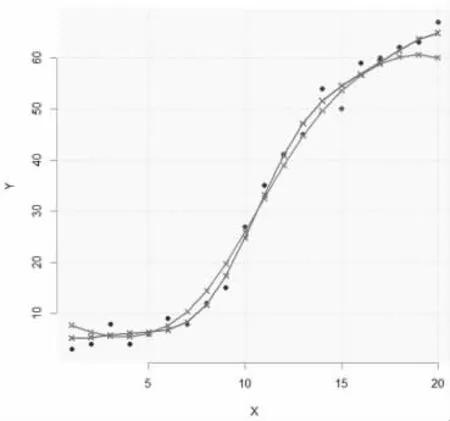
图8 SVR 超参数调优前后对比

6 结论

支持向量回归机已经广泛应用于诸多领域，皆取得了良好的效果，但其精度受超参数影响显著。本文通过使用网格搜索进行超参数优化,通过实验获得最佳SVR。下一步将考虑如何进一步降低误差值。