基于电导性能的原状土柱降雨入渗规律研究*

林昀昭 简文彬 豆红强 陈瑞敏 聂 闻

(①福州大学岩土与地质工程系，福州 350108，中国)(②福州大学，福建省地质灾害重点实验室，福州 350108，中国)(③中国科学院海西研究院泉州装备制造研究所，泉州 362200，中国)

0 引 言

我国是世界上登陆台风数量最多、自然灾害最严重的国家之一(张泰丽等，2016)。福建省地处我国东南沿海，地形以山地丘陵为主，地质环境复杂脆弱，是地质灾害频发的地区之一。根据统计，滑坡的变形和失稳90%以上与降雨有着直接或间接的关系(兰恒星等，2003)。受台风裹挟而来的暴雨将导致坡体变形，进而产生滑坡、泥石流。福建省花岗岩残积土分布广泛，因此开展坡残积土在降雨作用下入渗特性、水分运移规律的研究，对揭示由暴雨引起的滑坡、泥石流形成机制具有重要意义。

土体水分入渗是一个十分复杂的渗流过程，一般说来影响降雨入渗的因素主要包括降雨条件(雨型、雨强、降雨历时等)和土体性质(土体类别、渗透特性、初始含水率等)两方面内容。随着人工降雨技术的不断发展，降雨的可控性与便利性的不断增强，人工降雨试验是研究降雨入渗的最常见手段之一。藉此众多学者开展了大量试验研究，通过控制不同的降雨条件研究雨型、雨强、历时等因素对降雨入渗规律的影响。研究表明：土壤初始含水量越高，降雨强度越大，含水率传感器响应滞后时间越短(Montoya et al.，2017)。亦有学者在带有垂直人工大孔隙的土柱上模拟优先流作用下的土柱入渗，认为土壤中的优先流效应有助于雨水的入渗(Guertault et al.，2020)。但是，人工配置的扰动土柱无法完全契合真实的土层，为此，简文彬等(2020)利用人工降雨装置开展了原状土柱的入渗实验研究，探讨了不同雨强条件下土柱含水率、湿润锋以及入渗率等的响应规律。在边坡降雨入渗方面，学者们亦通过现场边坡降雨试验(孙萍等，2019)、室内边坡模型实验(沈佳等，2020)、现场调查与数值模拟相结合(卓万生，2020)等手段取得了丰富的成果。

电阻率作为反映介质水分赋存状态的有效指标，因其具有测试方便、快捷、廉价等优势，已在地基处理、滑坡潜在滑裂面判定等方面得到一定的应用(郭秀军，2004; 查甫生等，2006a)。更有部分学者使用电阻率含水率传感器、水势传感器等长期监测了整个斜坡不同位置的体积水含量、基质吸力和电导率。并进一步基于非饱和土强度理论，揭示了抗剪强度参数与基质吸力、电导率随时间的变化规律(Gance et al.，2016；Crawford et al.，2019)。可见，对水分分布特征及流动规律复杂的天然边坡而言，利用边坡土体电阻率反馈其含水率分布特征不失为一种有效方法，但相关研究仍较为鲜见。另一方面，由于原状土柱取样难度大，当前在开展一维土柱水分入渗的试验研究时多采用扰动土样，难以反映土体的真实入渗特性。

为此，本文以福建三明市梅列区洋溪镇岩兜滑坡为研究对象，开展原状残积土土柱降雨入渗试验，进而研究降雨作用下非饱和残积土土体的含水率再分布特征、电导变化规律与基质吸力变化规律。

1 研究区概况

滑坡研究区位于三明市梅列区洋溪镇岩兜村，属中低山地貌单元，整体地形坡度上陡下缓，坡面总体坡度25°～30°，局部陡坎达30°～40°。滑坡平面上呈圈椅状，主轴近东西向，斜长约50.0 m，高差约30.0 m。受雨水冲刷的影响，坡面土体流失，局部形成小冲沟。滑坡体及边界外围植被较发育。

三明市属亚热带海洋性季风气候，气候温暖潮湿，雨量充沛。年平均降水量约1635 mm，5、6月份降雨占全年45%左右，7、8月份常见暴雨，3～9月份为雨季，最大降雨强度为260.9 mm/24 h，50年一遇最大降雨量为314 mm/24 h。该滑坡变形历史较为长久，曾于1990年发生过山体滑坡。受2005年5～6月强降雨影响，滑坡又产生缓慢变形和滑动。变形区主要为山上的林地，坡面种植毛竹，植被覆盖率约80%，主要变形迹象表现在前缘堆积体分台阶下错明显、后缘开裂并下错(图1)。

图1 研究区概况图

2 原状土柱降雨入渗实验

2.1 试验土体

试验土体类型为花岗岩残积土，其物理力学参数如表1所示。采用直径为0.35 m、高为1 m的原状大直径土柱试件进行取样，首先选定所取土柱的范围，用锄头与铁锹挖去土柱附近的土体，让土柱初步成型。在靠近土柱范围后，用锉刀把大块土体削去，并用削土刀整平土柱表面。随后在土柱桶内涂抹凡士林，取样时在土柱桶顶面铺上木板，用大锤轻轻敲击以平衡土柱桶受力，将原状土柱装入土柱桶中。取样完成后，使用保鲜膜与胶带封紧桶口，减少桶内水分的蒸发。具体过程如图2所示。

表1 岩土物理力学性质参数

图2 原状土柱取样照片

2.2 试验装置

2.2.1 人工降雨系统

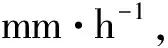
图3 降雨模拟系统主要设备

2.2.2 数采系统与监测元件

数据采集系统使用CR1000数据采集器和与其配套的LoggerNet自动采集软件。该套采集系统能够实时观察并记录试验过程中各监测元件数据。坡体含水率、电阻率的监测使用美国 Acclima 公司于2019年推出的TDR-310H传感器进行采集(图4)。TDR-310H是一个集成的时域反射计，结合了超快速的波形生成和数字化功能，提供土壤传播波形的实时时域分析，通过测量波导元件之间的土壤电阻来计算土壤导电率，介电常数的测量只和电磁波的传输时间有关，与测量电流、电压的大小和比例无关，保证了该传感器具有较好的稳定性；基质吸力的采集选用WATERMARK 200SS型多孔介质土壤湿度传感器(图4)。传感器由封装在颗粒基质内的一对超强耐腐蚀电极组成，通过固态电阻感应装置测量土壤基质吸力。

图4 土体监测元件

2.2.3 降雨土体入渗装置与监测元件布置

试验所用土体入渗装置为圆柱形有机玻璃桶，土柱桶高度100 cm、直径35 cm，厚度为0.5 cm。在土柱桶两侧进行开口并密封，以便于传感器的布置。本次试验在各个土柱桶两侧分别布置5枚TDR-310H传感器与WATERMARK土壤湿度传感器，电阻率含水率传感器编号从上到下依次为DT1～DT5，基质吸力计传感器编号从上到下依次为JT1～JT5，每个传感器间距为10 cm(图5)。

图5 监测元件布置

3 土柱降雨试验过程与结果分析

3.1 降雨方案与试验过程

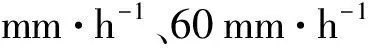
表2 岩兜滑坡土柱降雨试验方案

其中：实验1、2累计降雨量一致，均为300 mm，总降雨历时分别为15 h、9 h，主要探究累计降雨量一致情况下，不同雨强的干湿循环下雨水入渗规律；实验2、3降雨历时一致，累计降雨量分别为300 mm、420 mm，主要探究在累计降雨时长一致情况下，不同雨强的干湿循环下雨水入渗规律。实验3、4累计降雨时长均为9 h、过程降雨量均为420 mm，实验雨强一致，主要探究雨停时间对降雨入渗的影响。

试验过程中，将土柱安置在降雨装置下方，为了使土柱底端排水畅通，定制50 cm×50 cm底座，并铺设碎石和粗砂细砂，以保证土柱底部排水通畅并且土体不会被水流冲刷流出。同时，为了防止雨水沿原状土柱与土柱桶之间渗入，采用玻璃胶对顶部的土柱桶与原状土柱接触面进行了密封。

3.2 试验结果分析

3.2.1 累次降雨下土体含水率响应规律

图6即为不同循环降雨方案下土柱体积含水率随时间的响应规律。并将实验1在3次降雨作用下的土柱传感器响应时间汇总，如表3所示。

而在雨停期间，含水率慢慢降低，且表层土体下降幅度较大，实验1在第1次降雨结束后的21 h内DT1含水率由44.57%变为32.64%，降幅达11.93%。由于雨停时长仅为1 d，雨停后土柱各部分土体水分蒸发量有限，含水率均无法降低到降雨之前，存在上一次降雨所留下的水分，随着累次降雨的次数增多，留下的残余水分也越来越多，土体在每次降雨开始前的初始含水率也越来越高。观察表2，实验1在3次降雨前DT5的初始含水率分别为34.55%、35.72%、36.07%。

在累次降雨过程中，当降雨强度相同时，土柱上部传感器(DT1、DT2)含水率峰值随着干湿循环次数的增加而缓慢降低，降雨后的增长幅度与速率也相应变小。以实验2为例，第1次降雨DT1含水率峰值为44.57%，第2次降雨DT1含水率峰值则为43.84%，略微降低0.73%，且第2次降雨时含水率时变曲线斜率略缓于第1次降雨。这是由于受第1次降雨的作用，土柱上部土颗粒之间更加密实，孔隙率降低。土柱深部的土体则在累次降雨下，含水率峰值缓缓提高。这是由于在多次干湿循环过程中，由于降雨历时较短其强度较小，深层土体始终未达到饱和状态，随着干湿循环次数的增加，深部土体含水量逐渐累积，从而使含水率峰值提高。

对比图6a、图6b可知，实验1、2虽然总降雨量均为300 mm，但实验1第3次降雨雨强小历时长，雨水有效入渗量较大。这是由于在大雨强作用下，降雨强度大于入渗能力，无法入渗的雨水在土体表面流动形成坡面漫流，影响降雨有效入渗量(Ning et al.，2014)。因此累次降雨后，实验1深部土体含水率峰值较实验2高。实验2为大雨强短历时，土体含水率增加速率较快，对土柱表面冲刷更明显，使得上部土柱含水率峰值较实验1略高。

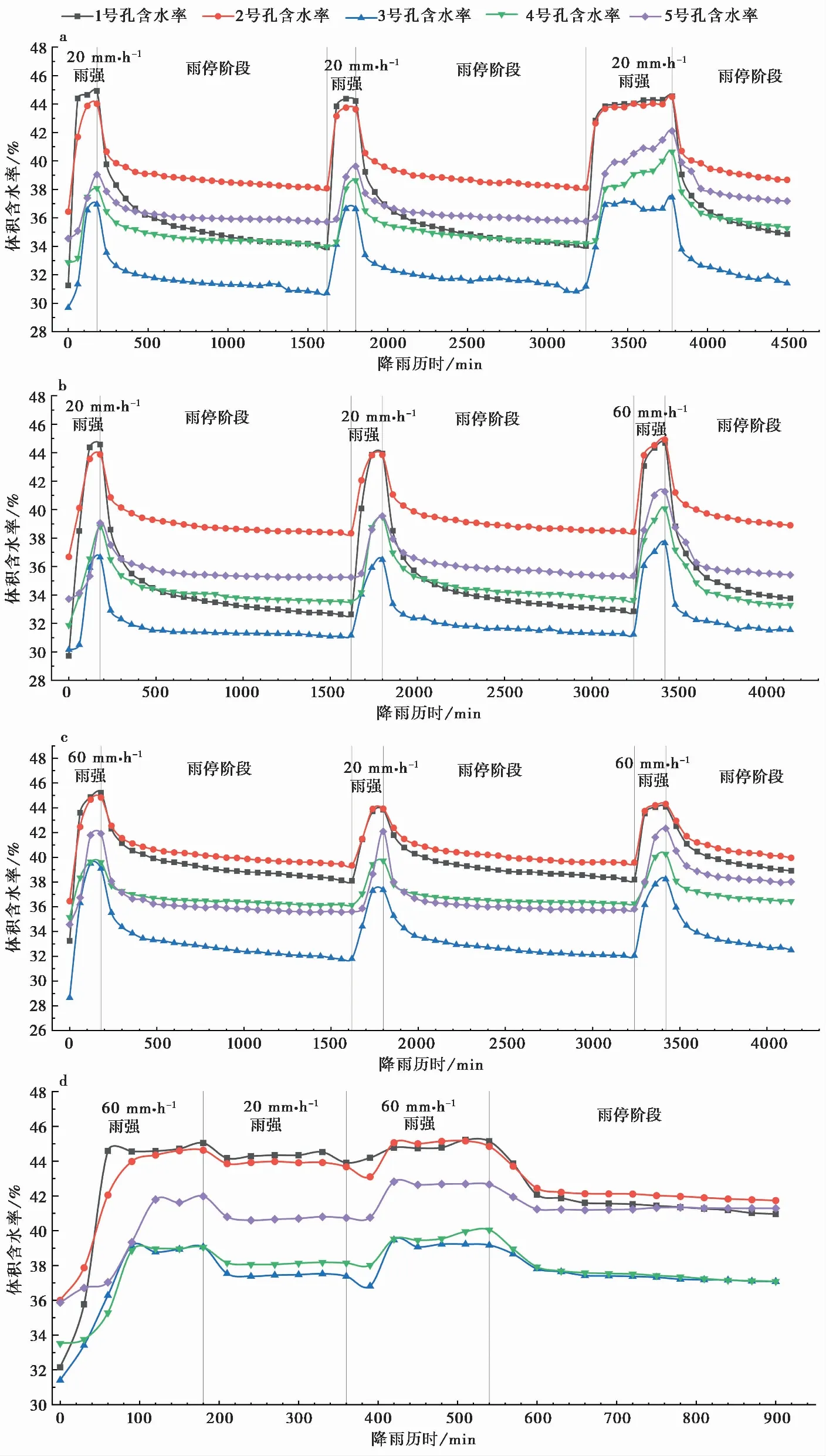
图6 累次降雨下岩兜土柱含水率时变曲线

对比图6b、图6c，实验2、3降雨历时一致，但总降雨量不同。雨强大小对土体含水率的影响主要体现在对降雨的响应时间以及饱和速度上，雨强越大，响应时间越快，饱和速度也越快。

对比图6c、图6d，实验4与实验3在雨强与降雨历时上一致，但实验4降雨结束后直接开始下一次降雨。对比实验3，虽然两次实验总降雨量一致，但是由于实验4没有雨停时间，因此没有退湿过程，所以实验4土柱各处的峰值含水率均大于实验3，但非常有限。这说明间歇性累次降雨虽然存在雨停蒸发时间，但在同等降雨量的情况下含水率峰值仍然能够接近连续降雨条件下的峰值。

3.2.2 累次降雨下土体电导响应规律

在不同的循环降雨方案下土柱电导性能变化规律由土体电阻率表示，其随时变的响应规律如图7所示。

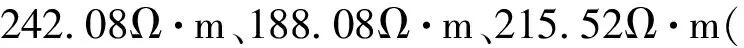
干湿循环中土体电阻率变化曲线并未像含水率变化曲线平滑，存在较多的小幅上下波动，这是由于土体电阻率受到含水率、孔隙率、孔隙水导电性等影响，变化的因素较多，因此在整体趋势变化的过程中会存在小幅波动。降雨开始后土柱上部土体电阻率从上到下依次开始响应，观察图7可知降雨时DT1、DT2的斜率大于DT4、DT5，上部土体电阻率降低速率与幅度大于土柱深部的土体。降雨结束后1～2 h内电阻率时变曲线会有一个较大幅度的回弹，但随后开始放缓，在雨停期间电阻率回升，但在21 h的雨停时间内无法恢复至初始值。随着干湿循环次数的增加，上部土体电阻率的最小值并未随着累次降雨越来越低，这是由于上部土体含水率峰值并未随着累次降雨越来越大，且雨水的多次冲刷改变了土体的离子含量进而影响了土体的导电性能。下部土体则由于在累次降雨下土体含水量越来越高，因而随着降雨次数的增加，土体电阻率最小值越来越低。

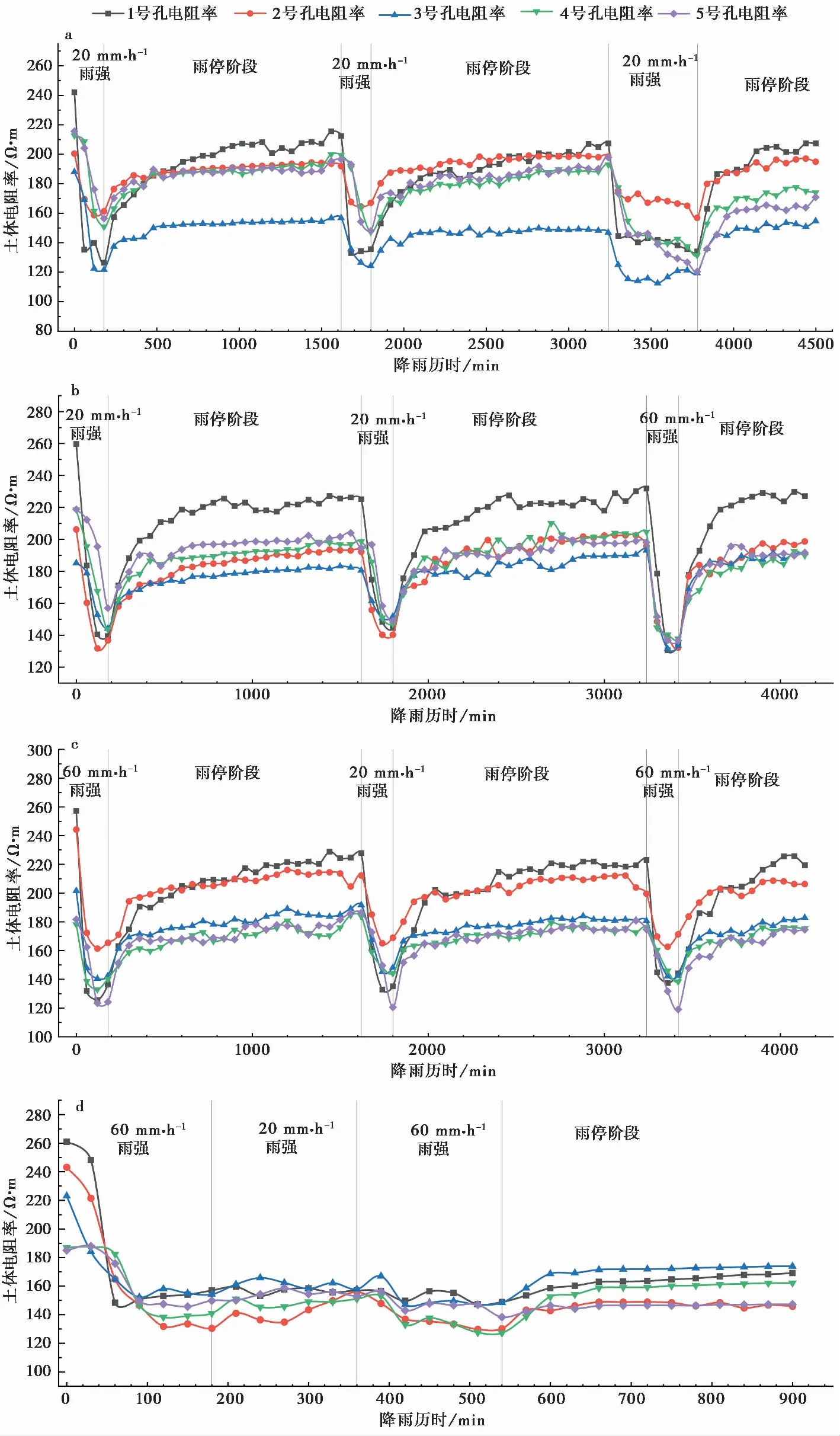
图7 累次降雨下岩兜土柱电阻率时变曲线

对比图7b、图7c，实验2、3降雨历时一致，但总降雨量不同，实验3总降雨量较大，入渗到土柱的水分更多，因此土体电阻率的降幅较实验2大。由图7d可以观察到，实验4没有雨停时间，在前后峰中间小的连续降雨雨况下，土柱各点的电阻率变化也呈现了先随着降雨快速降低，降雨强度减小，电阻率值略微回升趋于稳定，降雨强度变大，电阻减小并达到最低值3个不同阶段，电阻率对降雨及含水率具有较高的敏感性。实验3、4总降雨量与降雨历时一致，但实验4没有雨停时间，没有雨停时水分蒸发过程，因此在降雨后土体电阻率跌幅较实验3大，但其值十分有限。实验4在降雨120 min后，虽然雨水仍在入渗，但电阻率的变化速率已明显放缓。雨停后，实验3、4电阻率回升趋势总体相似，但实验4由于经历了长历时降雨，雨停后存留于土柱水分较多，因此相同时间内电阻率回升值略低于实验3。在相同的降雨量降雨历时下，雨停时间有限的累次降雨土体的含水率、电阻率变化幅度仍能十分接近长历时连续降雨，对滑坡的危害性仍然很大。

3.2.3 累次降雨下土体基质吸力响应规律

由于基质吸力传感器在雨停后回升较慢，因此仅取实验2、3的1、3、5号孔进行分析，在累次循环降雨作用下基质吸力变化如图8所示。

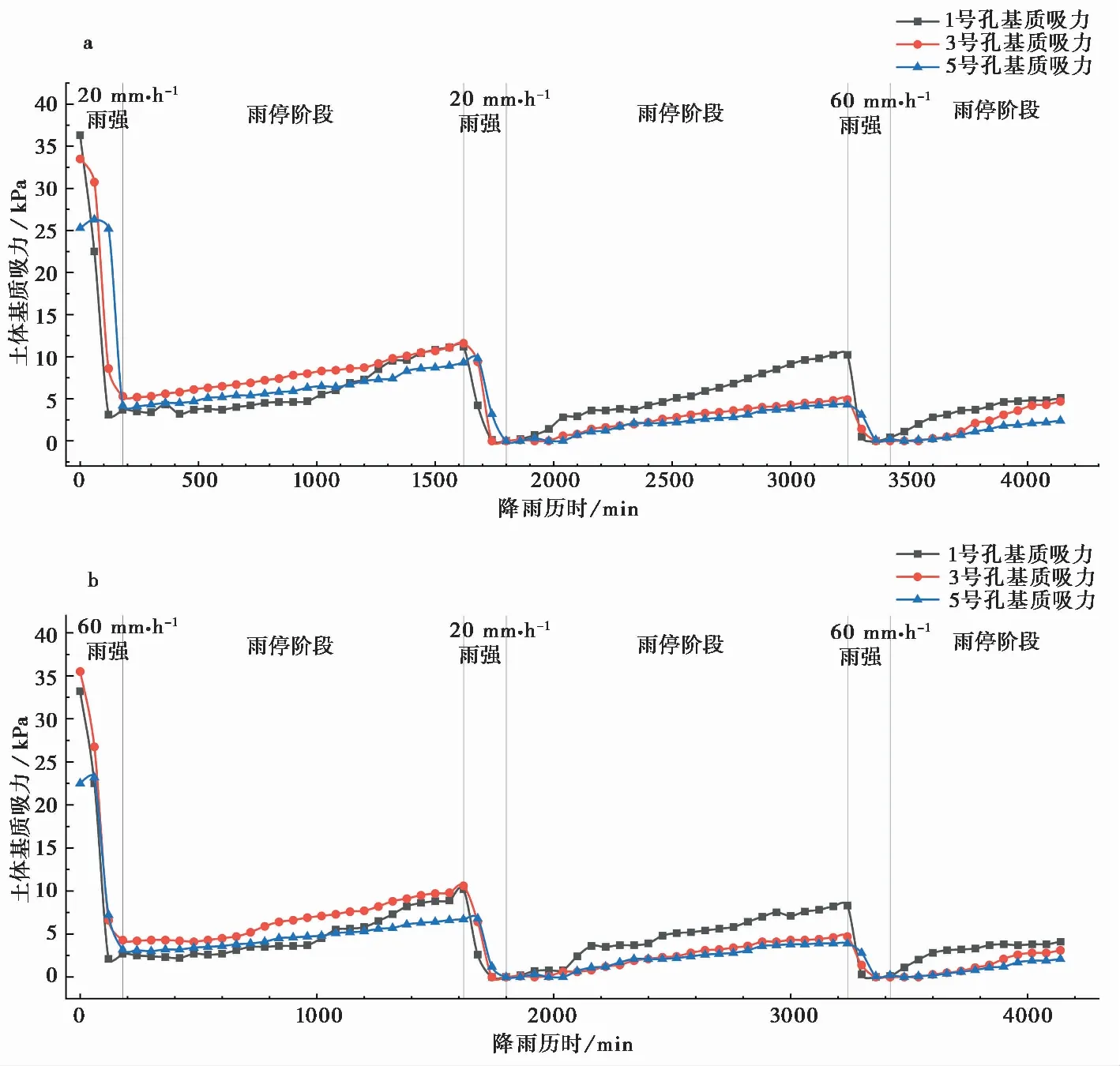
图8 累次降雨下岩兜土柱基质吸力时变曲线

在累次降雨中，第1次降雨后，基质吸力传感器由上至下依次开始响应，并在水分入渗后迅速降低，由于雨水入渗的滞后效应下部土体吸力响应时间较慢(实验2中JT1、JT3、JT5响应时间分别为30 min、50 min、130 min)，变化速率较小。土柱各部分基质吸力传感器的响应时间同步或者略微滞后于含水率传感器，这是由于在降雨过程中，土体吸力对降雨入渗的响应本质上是因降雨入渗引起土体内水分重分布而导致的，因此土体的基质吸力与含水率的变化紧密相关。实验2、3降雨历时一致，但实验3第1次降雨雨强较大，土柱各部分的基质吸力响应时间加快，变化幅度也更大，观察图8可知实验3第1次降雨中基质吸力时变曲线斜率更陡，变化速率较实验2快，降雨结束后各位置基质吸力值更低。实验过程中上部土体由于入渗更加充分土体饱和度更高，因此降雨结束后土体基质吸力低于深部土体，实验2降雨过后JT1基质吸力由37.6 kPa 降为3.7 kPa。在累次降雨的雨停阶段，基质吸力缓慢回升，但在21 h里3个点基质吸力回升的值非常有限，土柱上部相较于下部土体，水分能够下渗，并且挥发作用较强，在雨停期间水分下降较快，因此基质吸力回升幅度较大。实验3第1次降雨过后，JT1基质吸力由2.5 kPa回升到10.2 kPa，而JT3则只从3.1 kPa回升到6.7 kPa。从第2次降雨开始，土体由于上次降雨中留下的水分未完全排干，本就不高的基质吸力在多次降雨的作用下，纷纷降到0 kPa，累次降雨对基质吸力的影响得以显现。

3.3 土柱非饱和态向饱和态转变电导性能演化过程

根据试验所得的土柱电阻率、含水率、基质吸力对不同雨强历时响应规律，可进一步分析土柱从非饱和状态向饱和状态转变电导性能演化机制。降雨入渗前，土柱处于非饱和状态，基质势和重力势是影响降雨入渗的两个重要因素。土柱降雨入渗电阻率演化经历了3个阶段：①入渗初期主要受基质势主导，此时土体中的导电通路主要为土颗粒间导电与少量的土水相串而成的导电路径，入渗水分首先被土体颗粒吸收成为薄膜水，此时土水相串形成的导电路径初步增加；②随着下渗水分沿土体孔隙向下流动逐步充填孔隙，土水相串形成的导电路径大量增加，土体间的孔隙水得以连通，形成孔隙水之间的水路导电。由于土体为并联导电，此时即使只有少量的水分入渗，也会使土体电阻率有明显变化；③后期重力势发挥更大作用，水分在重力作用下呈稳定流动，进入稳定渗流阶段，孔隙水之间的导电路径也大量增加，形成了沿土颗粒传播、沿孔隙水传播、沿土水相串而成的路径传播三路并联的导电路径(图9)，从而导致土体电阻率大幅降低。

图9 残积土中电流的3种流通路径示意(据 Rhoadels et al.(1989))

4 残积土坡电阻率模型

4.1 电阻率与含水率关系

Archie于1942年通过对土的电阻率与其结构关系的试验研究，提出了适用于饱和无黏性土的电阻率结构模型(Archie，1942)，得出了饱和无黏性土的电阻率ρ随孔隙水电阻率ρw的变化关系式：

ρ=aρwn-m

(1)

式中：ρ为土体电阻率；ρw为孔隙水电阻率；a为土性参数；m为土性参数；n为孔隙率。

由于式(1)适用范围有限，Keller et al.(1966)将Archie模型拓展于非饱和土并建立了新的方程：

(2)

式中：Sr为饱和度；p为饱和度指数。

Archie模型由于未考虑土颗粒表面导电性对土体整体导电性的影响，因此适用范围有限，在孔隙水电阻率很小且土体中黏土矿物含量很低的情况下才能使用。对于黏性土等土颗粒表面导电性不能忽略的情况，Archie模型则不能适用。因此，Waxman(1968)通过两并联电阻试验提出了适用于表面具有导电性的黏性土电阻率模型：

(3)

式中：B为双电层中与土颗粒表面电性相反电荷的电导率；Q为单位土体孔隙中阳离子交换容量；BQ为土颗粒表面双电层的电导率，单位为1/(Ω·m)。

但由于Waxman公式参数较难获取，不利于在工程实践中推广。因此，选用改进的Archie公式对该滑坡点的坡残积土进行电阻率与含水率关系拟合。

土的体积含水率与土的饱和度密切相关，具体转换关系如下：

(4)

式中：θ为体积含水率；VW为孔隙水体积；V为土样总体积；w为含水率；γd为土的干重度；γW为孔隙水重度；n为土体孔隙率。

将式(4)代入式(2)可得土体电阻率与体积含水率关系式：

ρ=aρwnp-mθ-p

(5)

将土柱含水率、电阻率数据代入式(5)进行拟合，可得岩兜地区土体Archie模型如表4所示。为验证公式的准确性，在三明市岩兜滑坡现场选择剖面，插入TDR-310H传感器，并在坡面上进行野外入渗实验(图10)，测得现场土体在不同含水率下对应的电阻率数据。在测得数据中随机抽取20个点，将含水率值代入拟合公式，并用代入公式所求得的电阻率与实测电阻率值进行对比验证，求得偏差率。根据所求得结果，公式所求得的拟合值与实测值的偏差率为10.9%，误差较小(表4，图11)。

图10 野外现场测试剖面图

表4 含水率-电阻率参数拟合结果表

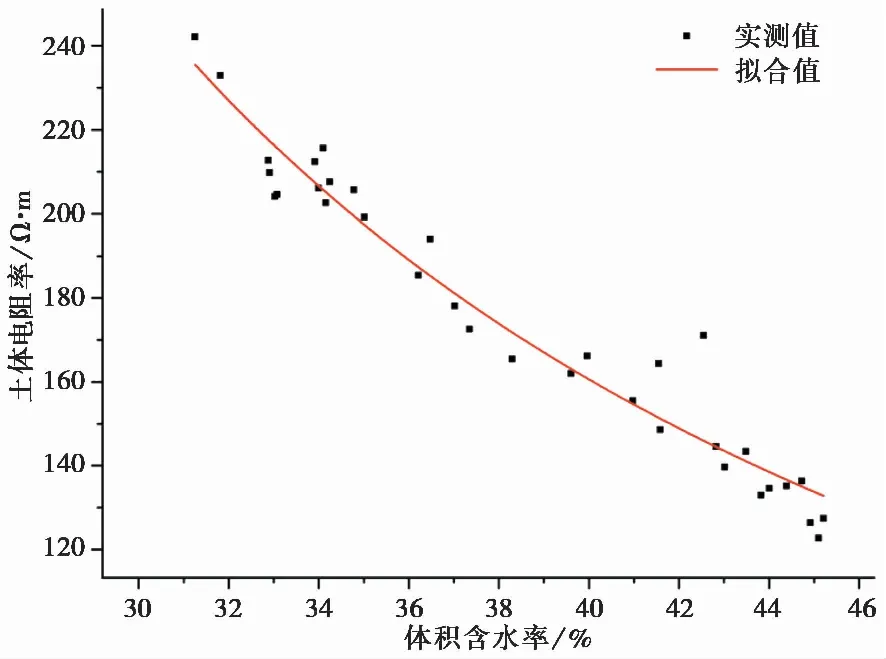
图11 残积土电阻率与含水率关系拟合曲线

4.2 基于电阻率的入渗模型

Green-Ampt入渗模型和 Philip入渗模型因具有明确物理意义(Green et al.，1911；Philip，1957)，有利于构建其特征参数与土壤物理性质间的关系，目前已得到广泛的应用与改进。有学者考虑坡体倾角和降雨强度的影响，提出适用于斜坡入渗的Green-Ampt 入渗模型(简文星等，2013；Dorofki et al.，2014)，Langhans et al.(2013)则考虑了微地貌对Green-Ampt 入渗模型的影响等，学者们不断引入新参数，提高了模型的适用性。

Green-Ampt入渗模型假定入渗过程为积水入渗时土壤剖面中存在陡湿润锋面，湿润锋面与土表面间的土壤处于饱和状态，并且湿润锋面处存在一个固定不变的吸力。Green-Ampt入渗模型可表示为：

（1）大型的机械设备，例如平地机、摊铺机和压路机等，需要在机械设备上粘贴红白相间或者黄黑相间的反光膜，在路边正常停放时，需要在周边放置警示标志，以便及时避让。大型机械设备车辆如果在夜间进行行驶，必须在能见度大于150m的条件下，才能正常行驶。对于压路机来说，还应该安装倒车雷达等装置。

(6)

式中：i为入渗率；ks为土体表征饱和导水率；h0为土壤表面积水深度；hf为湿润锋面吸力；zf为概化的湿润锋深度。

其中：表面积水深度可由实验条件来决定，概化湿润锋深度可由累积入渗量确定：

I=(θs-θi)zf

(7)

式中：I为累计入渗量；θs为土壤饱和含水率；θi为土壤初始含水率。

联立式(5)～式(7)，化简即可得到基于Green-Ampt 模型的土体电阻率入渗公式：

(8)

式中：ρs为土壤饱和电阻率；ρi为土壤初始电阻率。

Philip入渗模型则将入渗过程中任意时刻的入渗率与时间设为幂级数关系，即：

(9)

式中：i0为入渗率；S为土壤吸湿率；t为入渗时间；A为常数。

(10)

Philip入渗模型和 Green-Ampt 入渗模型的参数可相互推求(王全九等，2002)，在短历时入渗下，两模型参数存在以下关系：

S2=2kshf(θs-θi)

(11)

在长历时下则为：

S2=2hfA(θs-θi)

(12)

联立式(5)、式(10)与式(11)即可得到短历时入渗情况下基于Philip模型的土体电阻率入渗公式：

(13)

联立式(5)、式(9)与式(12)即可得到长历时入渗情况下基于Philip模型的土体电阻率入渗公式：

(14)

综上所述，基于电阻率的Green-Ampt与Philip入渗模型为土体入渗参量的测量增加了一种新的选择，同时得益于电阻率测量的便捷性(电阻率成像法等)，该法具备一定实践价值。

5 结 论

以福建三明市岩兜滑坡为研究背景，通过自行研制的人工降雨土柱入渗试验装置开展不同降雨强度下坡残积土的入渗试验研究，并得到如下结论：

(1)在降雨入渗过程中，土柱含水率由浅及深依次响应。随着降雨强度的增大，含水率变化速率也不断增大，且含水率峰值也随之略微提高。在累次降雨中，当降雨强度相同时，土柱上部传感器含水率峰值随干湿循环次数的增加而缓慢降低，降雨后的增长幅度与速率也随之变小。土柱深部的土体则在累次降雨过程中，土体含水量逐渐累积，含水率峰值缓慢提高。随着累次降雨的进行，在同等雨强下，土柱各个位置的响应速度均有不同程度的加快。

(2)原状土柱具有非均质性，不同深度土体电阻率大小不一。电阻率响应时间与含水率响应时间具有高度相关性，含水率与电阻率几乎同步变化，但两者变化趋势相反。

(3)基于Keller改进的Archie拓展模型对该滑坡点土体电阻率与含水率进行拟合，并用滑坡现场原型实测数据进行了合理性验证，结果表明该模型可准确揭示坡体含水率的变化。

(4)结合Archie拓展模型与Green-Ampt和Philip入渗模型，建立了基于电阻率的Green-Ampt与Philip入渗模型，为土体入渗参量的测量增加了一种新的途径。