基于COMSOL闭孔泡沫铝模型的导热系数分析★

余力洲，宋 臣，林 杰，付雨鹏，王海亮，缪玉松

(1.青岛理工大学理学院，山东 青岛 266525； 2.山东科技大学安全与环境工程学院，山东 青岛 266590)

1 概述

随着材料科学的不断进步，多孔功能性材料研究得到了迅速的发展，应用领域日益广泛，其中泡沫铝便是一种兼备金属和气体特征的新型多孔的功能结构材料，泡沫铝孔形的内部结构使其性能发生显著变化，与其基体材料铝或铝合金产生了较大的差异，使得泡沫铝材料具有了轻质密度小、高耐热性、耐火性、高抗冲击、高电磁屏蔽性、吸声隔音性、抗爆、易于加工等优点[1-4]。泡沫铝材料可以分为开孔泡沫铝和闭孔泡沫铝，闭孔泡沫铝为闭孔结构，开孔泡沫铝为通孔结构，其中闭孔泡沫铝材料具有优异的隔热性能，泡沫金属的导热性能与基体金属有关，随孔隙率或密度的降低而增加，开孔泡沫铝由于其通孔结构的高比表面积及复杂的内部对流条件而具有高的散热能力，相比闭孔泡沫铝的导热系数较低，被广泛应用为绝热材料。闭孔泡沫铝优秀的隔热等性能具有广阔的应用前景，因此研究泡沫铝材料热学性能具有长远的意义[5-6]。

目前，已有多种泡沫铝的仿真模型被广泛应用于力学、热学等领域的研究中。凤仪等[7]使用粉末冶金发泡法制备了闭孔泡沫铝样品进行试验，并与串联和并联孔、基体模型得到的模拟结果进行了对比，得出串联和并联模型能较好模拟闭孔泡沫铝模型导热系数的结论。覃静[8]依据面孔隙率等推导出的有规律的、简化的球形泡孔堆积的三维模型，研究了孔隙结构对温度场分布的影响，椭圆泡孔及泡孔排列方式、连通性等对导热的影响。李家卉等[9]基于Lu 模型的改进模型，进一步提高了模型的精度。赵昂通过调整模型尺寸、孔隙度、孔径范围和最小壁厚生成所需的泡沫铝夹层板二维随机圆模型，并探讨了孔径、孔隙率、基体材料对导热系数的影响。Coquard[10]利用立方体、十二面体、十四面体模型求解了导热系数。öchsner[11]依据立方体模型，使用有限元法求解出导热系数。泡沫铝模拟仿真主要研究闭孔泡沫铝的隔热性能，进一步求出其导热系数。由于试验所用的泡沫铝材料难以统一，泡沫铝物理试验需要的工作量较大，同时若想要以不大的工作量更为细致的研究泡沫铝的性能，常需要使用模拟仿真进行试验。关于泡沫铝的虚拟仿真，常使用近似孔隙的等效几何随机或规律分布绘制出二维模型结合理论公式等进行模拟，或提出三维模型进行模拟等。

为了解决现有泡沫铝模型不足的问题，本文提出了一种更合理的三维泡沫铝模型构建方法，避免了过多的假设条件，在数值仿真分析更接近实际情况，感官上也更具有直观性，边界设置等更为简单，相对二维模型拥有先天的优势。模型需要在MATLAB中合理设置相关参数，生成实际可用的三维模型，通过COMSOL有限元分析的软件中虚拟仿真，设置合理的边界条件进行模拟，求解出各种最大孔径、孔隙率参数组合情况下对应的导热系数，通过对大量的模型进行模拟仿真，总结出不同参数之间的关系，得出闭孔泡沫铝的导热系数及其规律。对比其他模型，本模型是一种基于随机球的模型、应用了迭代算法，能更好的接近模拟实际的闭孔泡沫铝模型，另外在有限计算能力的情况下模型能够模拟孔隙率为70%左右，理论上能够模拟较高孔隙率的模型，具有一定的应用前景。

2 三维仿真模型构建

2.1 生成模型

依据闭孔泡沫铝的物理特征，在模型构建前对闭孔泡沫铝内部孔隙-孔径之间的迭代关系、孔隙随机分布函数和近似为球体孔洞等假设。应用MATLAB软件开发了一套可以调整模型尺寸、最大孔径尺寸、模型孔隙率的程序。理论上本三维模型可以计算出95%以上的高孔隙率闭孔泡沫铝模型的数据，但受限于设备、时间等条件，在限制模型尺寸长宽高为10 mm×10 mm×40 mm长方体的条件下闭孔泡沫铝模型的最大孔隙率进行到85%，可基本满足模拟要求。

2.2 模拟仿真平台

模型经过MATLAB软件编辑程序生成模型后，经过ANSYS APDL生成实物模型，最终将模型导入到COMSOL进行仿真模拟，三维模型构建与仿真流程如图1所示。

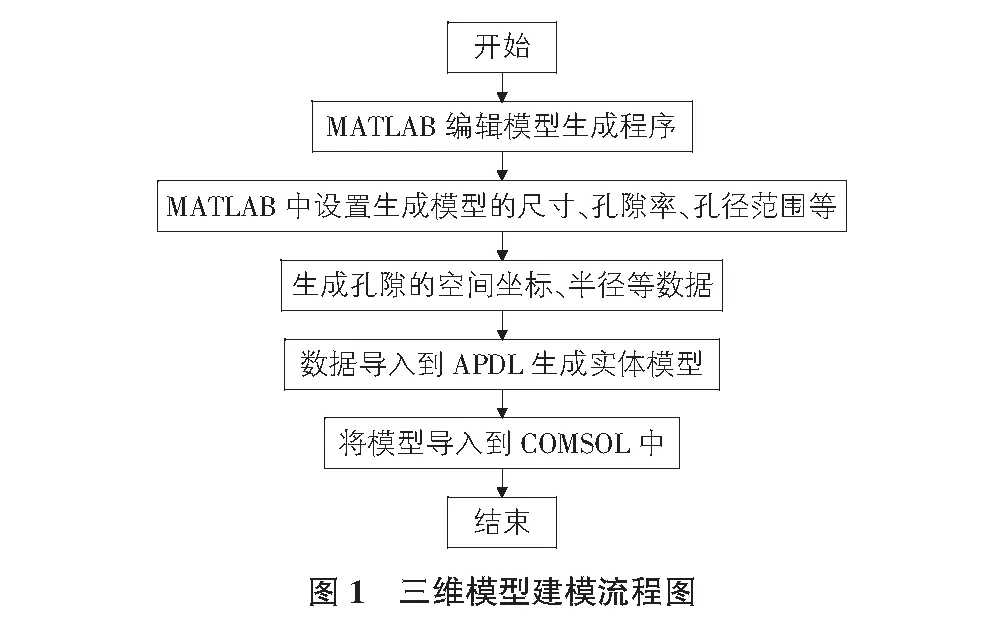
3 模拟仿真

3.1 模型建立及材料参数

本次模拟的闭孔泡沫铝材料选用导热系数为98.5 W/(m·K)的Al-10Mg 铝合金作为基体材料。模型中孔洞材料设置为空气，其余部分为泡沫铝合金。本模拟仿真在有限计算条件的情况下最大限度地求解出较高孔隙率的闭孔泡沫铝模型的导热系数，为避免泡沫铝模型厚度较小影响导热系数结果，经模拟测试比较，定义虚拟仿真模型尺寸为10 mm×10 mm×40 mm。

3.2 网格

将得到的各模型进行网格划分，根据孔隙率和孔径进行网格划分得到。以孔隙率60%孔径4 mm,8 mm为例。其中孔径4 mm最大单元大小6 mm，最小单元0.24 mm，最大单元增长率1.6，曲率因子0.7。孔径8 mm最大单元大小4 mm，最小单元0.24 mm，最大单元增长率1.5，曲率因子0.6。图2为网格图例。

3.3 热传导原理及边界条件

由于闭孔泡沫铝内部气孔为相对独立的椭圆或圆形个体，孔洞完全封闭无连接通道，气体很难形成流动，且泡沫铝最大孔径一般在8 mm左右孔径较小，对流作用可以忽略。而通过目前的理论和实验，对于闭孔泡沫铝来说，热辐射占传热比重较小，在10%以内，热辐射是可以忽略的，结合闭孔泡沫铝的传热路径，最终仅考虑热传导[12-14]。因此边界条件设置为：下表面为300 W/m2的恒定热通量，上表面设为自然对流，其余四面设为开放边界，环境温度为20 ℃。考虑到试验目的中有关孔隙率和孔径等参数对泡沫铝导热系数结果的影响，进行讨论分析，故虚拟仿真试验设置为对照试验，针对三维模型，设置泡沫铝孔隙率50%，55%，60%，65%，70%，以及其最大孔径限制值为4 mm，6 mm，8 mm设置为不同的组合，分别测定各个模型的导热系数值。

4 结果与讨论

4.1 有效导热系数的计算

根据上述设置的边界条件，我们通过COMSOL对闭孔泡沫铝三维模型进行仿真分析，经过计算得到了闭孔泡沫铝的上下边界的温度值，求解出两个边界的温差，根据傅立叶导热定律，求解导热系数。傅立叶导热定律的导热系数计算公式为[15]：

λ=-q/(dt/dx)

(1)

其中，λ为有效导热系数，W/(m·K)；q为热通量，W/m2；dt/dx为温度梯度，K/m；x为热流方向。

此外，本模型求解出的闭孔泡沫铝材料的导热系数与孔隙率的关系呈现出一种线性关系，即某一常数为系数的线性规律进行总结。依据现有情况，本模型的结果对比选用依据试验结果总结得出的理论公式，依据本模型得出的导热系数与孔隙率线性关系，经对比后选用Ashby提出的泡沫金属导热系数计算公式[16]:

λ=ξλ1(1-P)

(2)

其中，λ1为基体材料导热系数,W/(m·K)；P为孔隙率；ξ为材料特征值。

4.2 模拟结果

通过COMSOL稳态计算及式(1)得出，泡沫铝导热系数随孔隙率提高逐渐减小，这是由于一方面随着孔隙率提高，孔洞(空气)所占体积会增加，而空气导热系数比铝合金导热系数低很多，因此导热系数会随之降低。另一方面从结果图3中可以发现孔洞的存在会使传热路径发生改变，而闭孔泡沫铝存在大量的孔洞，这些孔洞对导热的传热路径有很大影响。孔隙率与最大孔径不同组合得到的导热系数如表1所示。

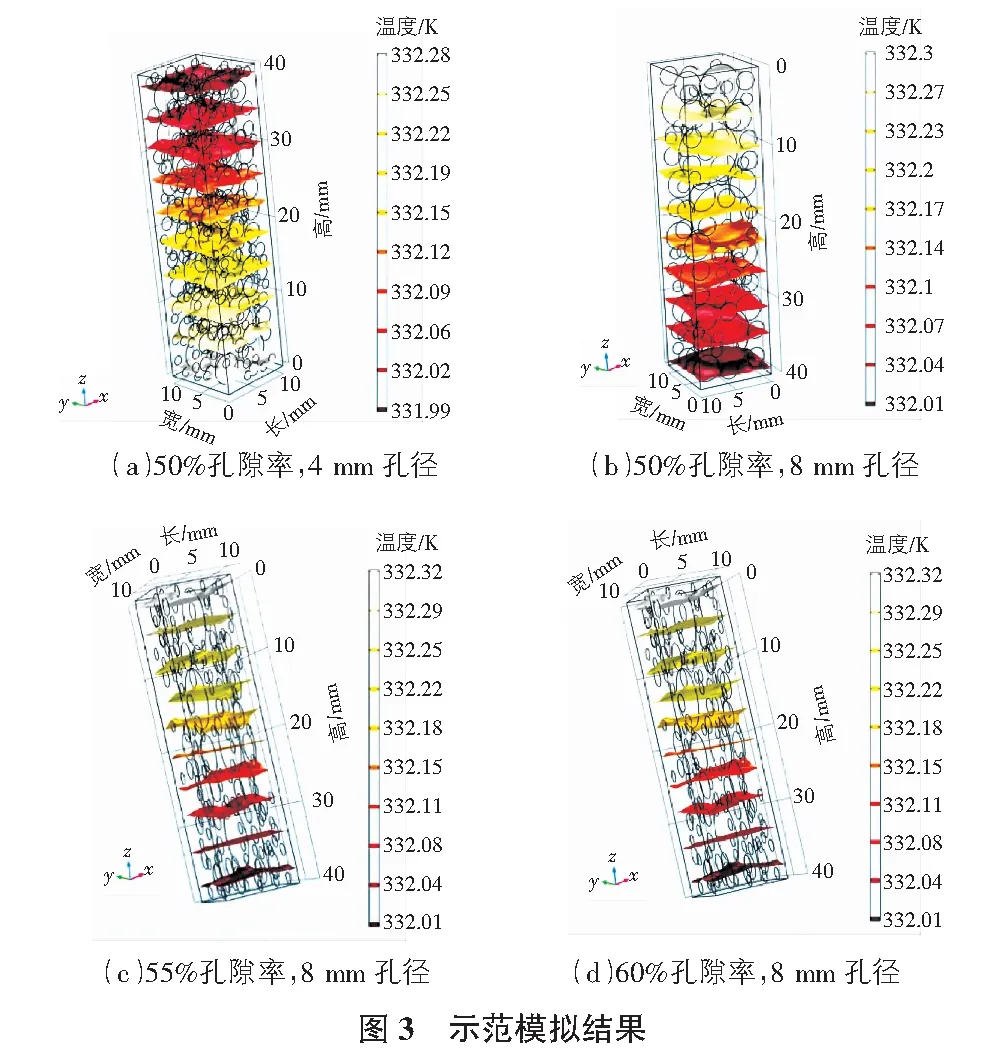
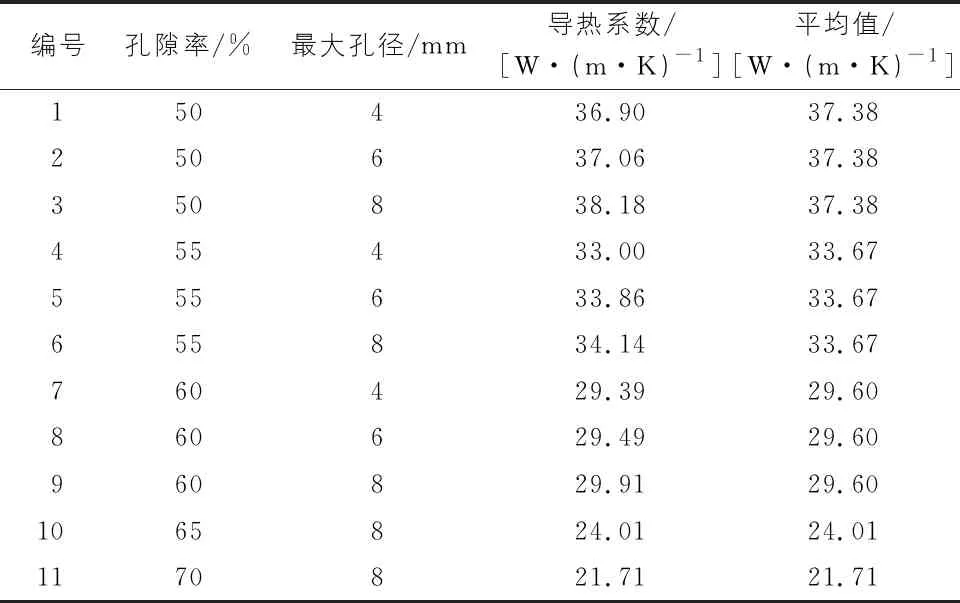
表1 模型导热系数

4.3 讨论

将最大孔径为8 mm的各个孔隙率泡沫铝组合进行统计得到如图4所示的规律曲线及其拟合曲线：

y=-0.861 4x+81.274

(3)

其中，x为孔隙率；y为导热系数。

图4显示了闭孔泡沫铝导热系数随孔隙率的增加而呈现线性降低，孔径对导热系数的影响很小。这表明孔隙率对导热系数的影响占主导作用，在很大程度上它能够反映闭孔泡沫铝的导热系数，这与目前关于闭孔泡沫铝研究结果是一致的。

为了进一步验证仿真结果的正确性，将仿真结果的拟合曲线与公式计算得到的结果进行对比。从图4可以看出，仿真结果与理论结果均呈线性下降且与理论结果有小范围差异，说明本文采用的三维泡沫铝模型能够较好地模拟泡沫铝在不同孔隙率及孔径下的导热情况。对于仿真结果与理论公式计算值之间的差异，原因可能与模型尺寸、气孔的形状、大小和结构形式等有关。

根据图5拟合曲线及理论公式计算曲线可以观察出，随着孔隙率的增加，误差也开始减小，可能存在着高孔隙率的泡沫铝材料中孔隙率对导热系数的影响会更大，而孔的大小和结构形式对其导热系数的影响会降低，模型尺寸造成的误差影响的比重逐渐较小的情况。

5 结论

1)本文基于MATLAB及ANSYS生成随机分布球的闭孔泡沫铝模型，通过COMSOL进行不同孔隙率及孔径的仿真实验，得出了可以很好地描述闭孔泡沫铝的导热系数曲线。

2)基于本次仿真实验，得出闭孔泡沫铝随孔隙率的增加，导热系数会随之降低的规律，得出闭孔泡沫铝导热系数与其孔隙率之间的关系近似于线性。

3)泡沫铝的导热系数值很大程度取决于孔隙率的大小，孔径对导热系数影响较小，在50%～60%孔隙率范围内最大孔径闭孔泡沫铝导热系数结果误差在3.55%～1.77%。

4)由于计算机的限制，高孔隙率的导热系数未被模拟计算。因此后续导热系数仅给出了参考值，在已有模拟结果与经验公式对比下，参考值结果可靠，符合客观规律。