改进条分法对降雨和荷载作用下浅层滑坡分析★

孙艳杰，王石磊，林丽芳

(中科路恒工程设计有限公司，山西 太原 030006)

1 概述

根据相关文献[1-4]可知，降雨和坡顶荷载是引起边坡失稳的重要原因。降雨入渗导致坡体非饱和土含水率增大抗剪强度减小[5]；边坡在上部荷载作用下会产生不通过坡趾或坡趾下方的滑裂面，增大边坡失稳风险[6]。

边坡稳定性分析研究包括有限元法[7-8]、试验法[9]和极限平衡分析法[10]。有限元法将坡体看作是有限个单元体连接而成，各个单元体边界由数学函数表示，该方法往往对于均质土体有较为准确的分析结果，不适用于非均质土体，且对土体物理参数的赋值较为困难；室内或现场试验对坡体发生失稳的过程和结果观测准确，但是难以对边坡失稳机理进行说明；极限平衡法主要有毕肖普条分法[11-13]、折线滑动法[14-15]和瑞典条分法[16-19]等。本文基于瑞典条分法、摩尔库仑理论、弹性理论和Mein-Larson入渗模型得到了坡顶荷载作用下、降雨入渗下和降雨与坡顶荷载耦合作用下的边坡稳定性分析方法，旨在对边坡稳定性分析的理论和实践提供参考。

2 方法简介

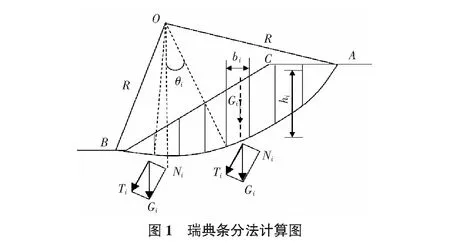
瑞典条分法[20]其计算图如图1所示。图1中，土条的自重为Gi，bi和hi分别为土条的宽度、平均高度。土条法向应力为Ni，滑弧相切的剪应力Ti。法线与竖直线的夹角为θi，其中Ni=Gicosθi和Ti=Gisinθi。

(1)

若将整个滑动土体内各土体对圆心O取力矩平衡，则∑TiR=∑TfiR，故边坡稳定性系数为:

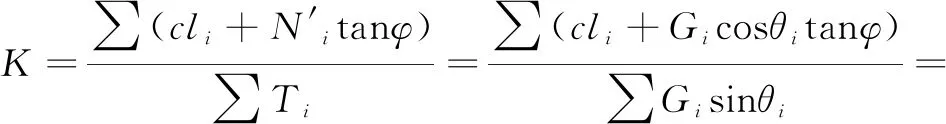
(2)

基于瑞典条分法稳定性系数表达式分别对降雨条件下和坡顶荷载作用下的边坡稳定性系数进行求解:

1)由于降雨强度和降雨时间的不同，降雨入渗深度在不同的降雨条件下会存在较大差异，入渗深度越深坡体的含水率越大。土体的含水率越大其相对应土体的重度越大，滑动面的下滑力也就越大，边坡越容易发生失稳。本文对降雨入渗深度计算，求出滑动面上饱和带与非饱和带土体重度，并根据瑞典条分法得到降雨条件下边坡稳定性系数表达式。

2)坡顶荷载作用对滑动面不同位置的影响是不同的。利用摩尔库仑理论和弹性理论将滑面各个点的受力情况进行分析，得到不同点的强度表达式，利用微积分与极限平衡理论得到坡顶荷载作用下边坡稳定性系数的表达式。

3)对滑动面上受到降雨影响或坡顶荷载影响下土条的受力情况进行联立分析。

3 边坡稳定性系数求解

3.1 降雨入渗下边坡稳定性系数

Mein-Larson入渗模型[21]设降雨后的土体含水率以湿润锋为临界线，锋前后分别为天然土体含水率Qi和饱和土体含水率Qs。坡顶有积水存在，湿润锋处吸力不变。

在发生降雨的情况下，出现入渗现象。降雨入渗深度与降雨强度、时间有关。当雨强大于土体饱和渗透系数时，入渗率可以用式(3)表示[22-23]。

(3)

(4)

当坡顶积水时间为tp时，降雨累计入渗量Ip与降雨时间tp如式(5)和式(6)所示。

(5)

(6)

其中，q为降雨强度；α为边坡坡度。则不同降雨时间内的降雨入渗量如式(7)所示。

(7)

其中，ts为坡顶开始积水到累计降雨入渗量Ip所用的时间。根据式(4)则降雨强度大于土体饱和渗透系数时降雨入渗深度如式(8)所示。

(8)

当降雨强度小于土体饱和渗透系数时，降雨全部入渗到土中，可以将降雨入渗率看作为降雨强度，由于边坡存在坡度，则此时降雨入渗量可以用式(9)表示。此时降雨入渗深度如式(10)所示。

I=qtcosα

(9)

(10)

根据式(2)可以得到降雨影响下边坡稳定性系数表达式如式(11)所示。

(11)

本文将滑动面看作是一条直线，将入渗深度设为与坡面平行的一条直线，则降雨后滑动面面积可以看作为饱和带S1与非饱和带S2，如图2所示。

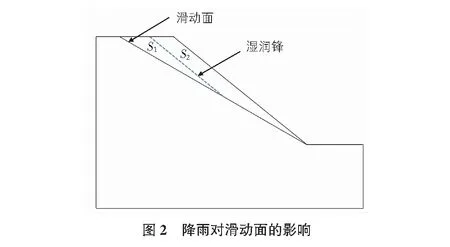
坡肩到滑面距离为D，滑面两端垂直距离为h。则降雨影响下边坡稳定性系数表达式可以转变如式(12)所示。

(12)

(13)

(14)

3.2 坡顶荷载下边坡稳定性系数

设边坡顶上有一均布荷载P，滑动面为一条直线，如图3所示。

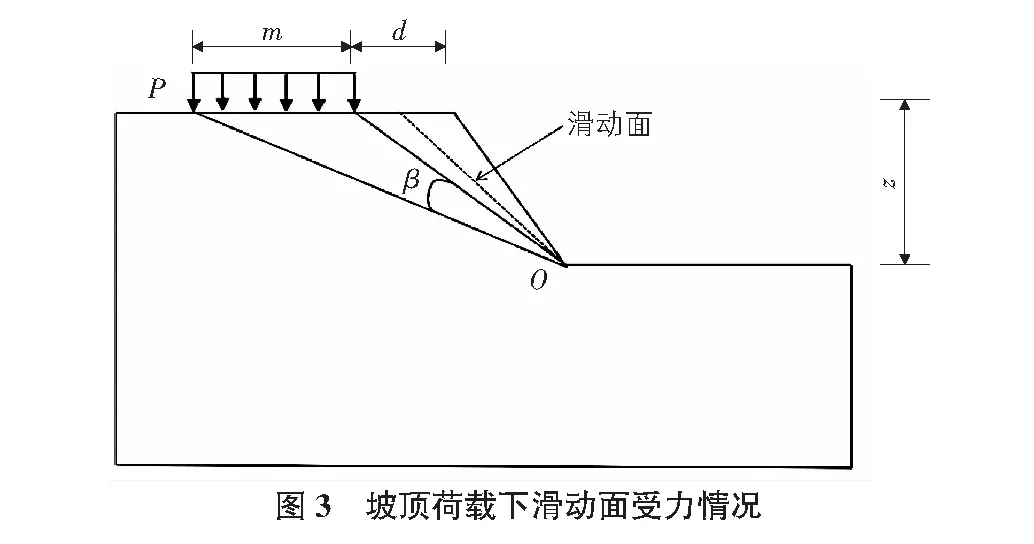
图3中，d为荷载与坡肩距离；O为滑面某一点；β为O点到荷载作用面夹角。

当荷载作用地基时，荷载会使地基以下某点的受力产生变化。本文设此点为滑面上某一点。此点大小主应力如式(15)和式(16)所示。

(15)

(16)

根据摩尔-库仑理论，O点处剪应力和抗剪强度用式(17)和式(18)所示[24-25]。

(17)

τf=c+σtanφ

(18)

(19)

其中，α′为应力夹角；φ为内摩擦角；c为黏聚力。

则O点处所受剪应力和抗剪强度如式(20)和式(21)所示。

(20)

(21)

设O为正方形单元，式(20)和式(21)可以转变为式(22)、式(23)。

(22)

(23)

根据式(17)可以得到坡顶荷载作用下边坡稳定性系数表达式，如式(24)所示。

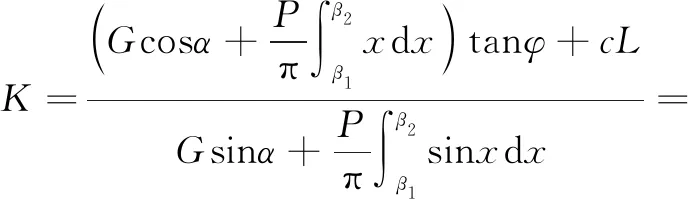
(24)

其中，L为滑面长度。

由图3可知，β1位于坡顶，则β1为0°，则式(24)可以简化为：

(25)

3.3 降雨和坡顶荷载耦合作用下边坡稳定性系数

由于降雨对滑动面土条的影响包含水压力的作用，因而将式(12)和式(25)进行联立，得到降雨和荷载耦合作用下边坡稳定性求解式，如式(26)所示。

(26)

G′=S1γ+S2γsat

(27)

4 改进条分法算例

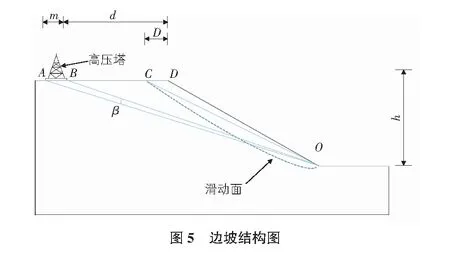
山西省某地在建公路项目，地形复杂，夏季雨水集中在7月～8月，雨季地质灾害多发。根据现场地质勘察，发现该地某一边坡，距离坡肩20 m处有高压塔存在，边坡发生时可能危及高压塔的安全，影响输电区域的用电，如图4所示。本文对工程实际情况进行建立，如图5所示。

边坡相关参数如表1所示，其中降雨条件以10年7月～8月降雨情况为依据设定。

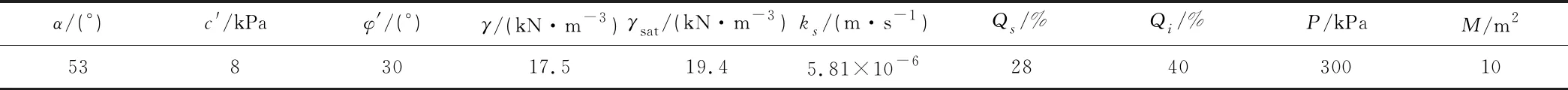
表1 边坡体相关参数取值

其中，D=2 m，h=32 m，β=7.47°，根据式(10)可以得到降雨入渗深度为0.83 m，根据现场情况设5条滑动面，相关参数如表2所示。

表2 不同滑动面参数及稳定性情况

从表2中可以看出，在该降雨条件下边坡整体上处于不稳定状态，容易发生失稳。GEO-STUDIO操作简单工程应用性强，为了对结果进行验证此处利用GEO-STUDIO对工程进行模拟，GEO-STUDIO建立的数值模拟明显如图6所示，计算结果如表3所示。

从表3可以看出，两种方法的计算结果基本一致，稳定性系数随着滑动面而变化，均呈现一种由小增大的变化趋势，且边坡最终判定结果均不稳定。

表3 GEO-STUDIO稳定性系数计算结果比较

5 结语

1)改进瑞典条分法建立了降雨条件下边坡稳定性求解式；以弹性理论和摩尔库仑理论为变换条件基于瑞典条分法得到了坡顶荷载作用下边坡稳定性系数表达式；对两种表达方式进行有机结合得到了降雨和坡顶荷载耦合作用下边坡稳定性系数表达式。

2)针对工程实际，建立了相应的边坡模型结构，并以坡顶裂缝为剪出口设定了5条滑动面。根据边坡稳定性系数表达式对所设滑动面的稳定性系数进行求解，稳定性系数均小于1.2，结果表明在降雨情况下边坡整体呈不稳定状态，判定结果与GEO-STUDIO计算结果基本一致。

3)本文设滑动面为一条直线，随着滑动面厚度的增加计算结果与实际情况差别会变大，因而该方法只用于浅层滑坡失稳，后续将继续对滑动面进行改进。