基于点云数据的铁路轨道线形提取方法研究

张匡宇，田 庆

(陕西铁路工程职业技术学院，陕西 渭南 714000)

既有线改造与维护和既有线增添二线都需要线路勘测技术，传统的既有线勘测使用全站仪与水准仪进行测量，稀疏目标点高精度数据采集模式从理论、设备到应用非常成熟，但存在局限性，加之传统线路勘测手段有效率低下、作业安全隐患大和人力成本高等诸多问题，线路勘测作为铁路工程数据源，需要引入和现代铁路工程特性相匹配的数据采集新技术[1]。高效三维立体的勘测方法成为了既有线铁路勘测的实际需求。

地面三维激光扫描技术(Terrestrial Laser Scanning,TLS)通过测量物体表面密集点的三维坐标和反射率，通过加工点云还原出被测目标的三维模型的一种全自动测量技术，具有高精度，高效率，全天候等诸多优点[2]。目前，三维激光扫描技术已经应用在文物保护、变形监测、土方体积计算等领域。徐进军等将三维激光扫描技术引入到滑坡变形监测于分析领域，并充分利用滑坡体上自然物的大量点云作为监测点来完整和分析其变形[3];阎海波等将三维激光扫描技术引入到地铁盾构区，通过对点云的拼接，去噪等技术处理实现了盾构区三维重建[4]；王军将三维激光扫描技术应用到古建筑保护领域，采集古建筑点云数据并完成文物点云模型的构建[5]。

将三维激光扫描技术应用到铁道勘察领域，可对目标立体勘测，外业数据采集效率高，数据精度高，进行外业扫描作业时，操作人员不需要直接与轨道接触，在轨道外即可完成点云采集，作业人员相对更为安全，并且扫描作业期间列车也可正常运行。目前三维激光扫描技术在铁路工程领域应用处于起步研究阶段，本文主要研究三维激光扫描技术在铁路轨道线形提取的技术过程。

1 点云数据的采集与拼接

通常被扫描的工程体积大，或者结构复杂，一次扫描不完全，需要多次扫描，各自扫描得到的点云数据是在各自的坐标系下存在的，需要将各站点云拼接到统一的坐标系下，这个过程叫做点云拼接。常用的点云拼接方法有标靶拼接和控制点拼接。标靶拼接需要在相邻的两测站放置至少3个公共标靶，为了减小拼接误差，通常视具体工程多设置几个。相邻两测站扫描可获得各自测站的点云数据，其中包含了各自测站坐标系下的公共标靶相对位置，相邻测站点云数据两两拼接，直至全部测站拼接完成，拼接采用的数学模型是布尔莎七参数模型(B模型)；控制点拼接原理下，要求所有点云(包括标靶)在采集过程中整体完成定位定向，再将每一测站扫描得到的点云数据通过坐标转换解算到同一个坐标系下。对于铁路轨道这样的线形结构物，控制点拼接扫描的外业效率较高，拼接工作量较少，且拼接容错率较高，相较于标靶拼接有较大的优势[6]。本次轨道原始点云采用的是控制点拼接。

在控制点拼接原理中，扫描仪扫描的三维激光点云各点的相对位置是固定不变的，拼接时可以将点云看作整体一次性进行拼接，其中标靶点云代替整个点云参与拼接计算。这种拼接的实质是将各测站独立坐标系中的点云分别转换到地面控制点所在坐标系中。设有控制点a和控制点b，它们的平面坐标为(Xa,Ya)，(Xb,Yb),则ab的方位角αab为：

(1)

设b测站测得整体点云为p，则bp的方位角αbp(左角观测)为：

αbp=αab+β-180°

(2)

点云p的坐标为：

(3)

其中，Zp为点云p的高程；Zb为控制点b的高程；Sbp为测站b到点云p的斜距；θbp为测站b到点云p的竖直角。在实际计算时，用标靶代替整个点云参与计算，各个测站扫描的点云p通过整体坐标的位移和旋转变化，就可以统一到控制点所在的坐标系中。

本次外业扫描设计共有8个控制点进行设站，先通过全站仪精确测量控制点三维坐标，本次测量的8个控制点的坐标采用独立坐标系，控制点坐标如表1所示。

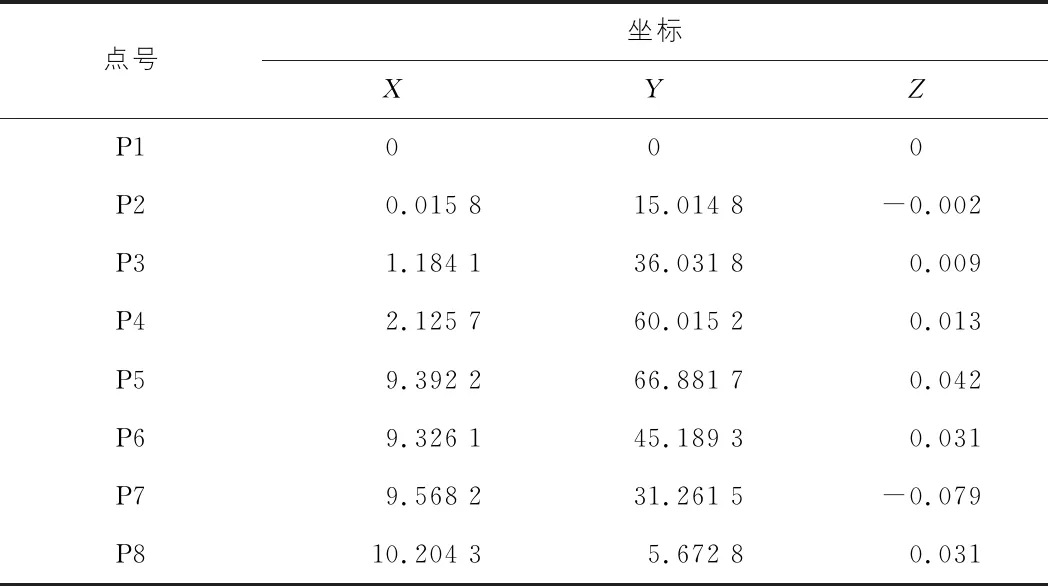
表1 控制点坐标 m

以P2控制点设站为例，首先，在P2控制点安置三维激光扫描仪，对中整平，在相邻的P1控制点上安置标靶并对中作为后视点，P2扫描仪使用P1标靶进行后视定向，此后每一站依次类推，每测站设置扫描仪分辨率，扫描质量等参数不变，以上一个相邻的控制点为后视点进行后视定向，完成全部的测站扫描，扫描得到铁道点云的同时获得标靶在扫描仪坐标系下的相对坐标。

本次点云拼接作业使用的是HDScence，一款专门用于地面三维激光扫描仪点云拼接的软件。在采集铁道原始点云数据时使用的是控制点拼接模式，点云拼接使用相匹配的“一键式拼接”完成各站点云拼接，首先将各个测站点号和三维坐标以及后视点号和三维坐标严格按照要求格式每行写在txt文件中，再用软件读取txt文件，将所有的测站点云一次性拼接完成[7]。

2 点云数据处理

2.1 点云选取

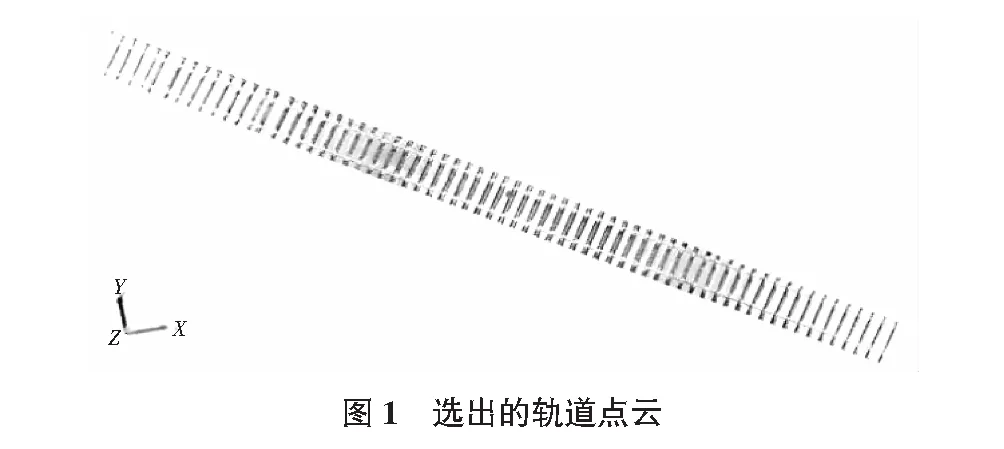
在进行铁道点云数据外业采集时，扫描仪对周围物体是无差别扫描的，因此原始点云中扫进了周围大量的无用点云数据，远远超过有用的点云数据，造成数据冗余。依工程需要可根据点云所处位置不同进行首次选取，删除掉多余的点云数据，图1为在点云操作软件中选出的轨道点云。选出的点云依旧包含冗余点云，如轨枕，道床，扣件等。由于轨道的结构较为复杂，且轨道的位置高低不一，这些冗余点云和轨道点云数据紧密混杂在一起，不便于选取，需要算法对这些点云进一步分割提取。

根据钢轨高于枕木及道砟的特点对钢轨点云进行判别并提取。具体做法如下：

第一步:将带有冗余的点云数据在二维上进行网格化处理。找到点云数据中所有点的xmin，ymin,xmax和ymax，以(xmin，ymin),(xmin，ymax),(xmax，ymin)和(xmax，ymax)为四个顶点构建一个包含全部点云的矩形网格。

第二步:将大网格以边长为0.3 m分割成若干个小网格。按照网格横纵坐标依次给每一个小网格排序i，在每一个网格i中搜索该网格中点云各点z坐标的最大值zimax，zimax即为i小网格钢轨轨面最高高程。

第三步:设置滤波阈值h的大小，每一个小网格i中，点云数据中坐标z小于zimax-h则被看做是钢轨以下的点云数据，予以剔除，高程z不小于zimax-h的点作为钢轨点云数据予以保留。为了保证效果，h的取值宜在55 mm～60 mm之间，实际证明，此时没有过多的有用钢轨点云数据误删，也没有留下太多的冗余数据。

图2为有效地剔除了枕木、扣件、道砟的点云。

2.2 点云滤波

受地面三维激光扫描仪设备自身的精度、目标对象钢轨的表面反射、现场实测环境等的影响，去除了冗余点云之后的钢轨点云数据中依旧包含有许多噪声点，这些噪声点和钢轨点云混杂在一起，没有规律，随机出现，大小在毫米级别，会对轨道点云整体造成精度影响，无法通过有效的手段剔除，只能采用算法将噪声点滤波。

本次采用的是拉普拉斯滤波法，其原理是对点云的每一个点采用laplace算子，laplace算子定义如式(4)所示：

(4)

点云进行拉普拉斯滤波的过程，实质上是点云噪声的稀释过程。设Pi为点云中任意一个待处理点：

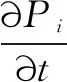
(5)

对上式进行积分，那么点云中包含的微小噪声数据会迅速发散到该点的邻域中，而正常的点云发散的速度会很小，几乎不产生位移，这样就达到点云滤波的效果。如果采用显式欧拉积分方法，即为：

(6)

采用该方法处理点云数据，每一个点都使其逐步移动到其邻域的质心处：

(7)

其中，qj为Pi的第j个邻域点；λ为较小的正数;点云滤波中wj为临近点至点Pi的距离的倒数。

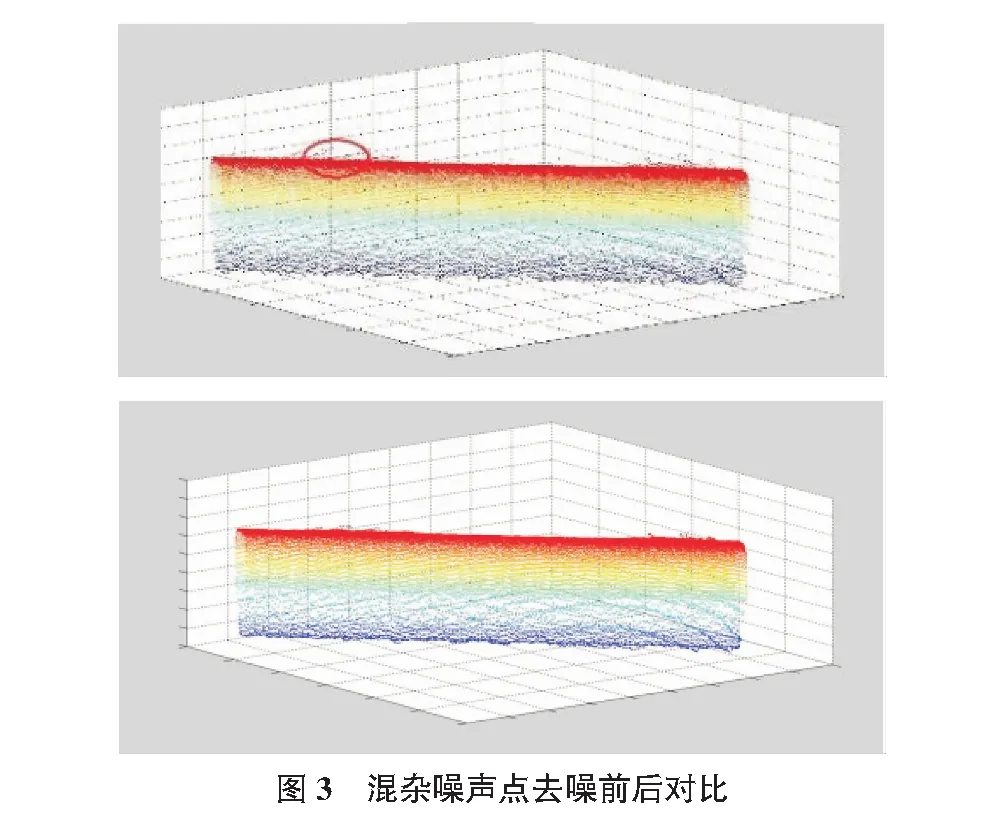
通过滤波处理进行了数据平滑，轨道模型细节没有缺失，噪声点尖锐部分消失，有效降低了微小噪声点对轨道模型造成的误差。轨道点云模型混杂噪声点滤波前后对比如图3所示。

2.3 点云精简

以滤波后的轨道点云为对象，对点云进行精简。点云精简的目的是通过减少点云的数量使点云处理算法运行速度更快，同时点云模型的精度不会减小。

本次精简采用的是立方体重心法。先建立一个大的立方体，使全部点云被包含到该立方体中，再按一定的边长三维分解立方体，得到许多个大小完全相同的小立方体，把没有包含点云的小立方体从该群体中剔除后，剩余立方体的重心替换小立方体中的全部点云。使用立方体重心算法，精简掉了62.5%的点云，精简后的点云密度变得一致，数据量大大减小，为后续点云计算做准备。

3 轨道线形提取

以上述步骤处理过的轨道点云为数据支撑拟合轨道线形[8-9]。由于拟合长距离直线线形个别位置误差会增大，为保证线形的准确性，采用分段拟合方法。截取了其中一段轨道点云进行直线拟合，拟合直线使用的是最小二乘法，它通过使各个点到拟合直线距离的平方和最小从而寻找点云的最佳直线函数匹配。现假设点云数量为n，拟合的直线方程为y=kx+6，那么误差表达式为：

(8)

分别对上式关于k和b求偏导数得：

(9)

(10)

整理上式得：

(11)

(12)

解出上式方程，得：

(13)

(14)

通过轨道点云数据拟合出的直线如图4所示，两直线的斜率与截距参数为k1=-0.543 6，b1=3.594 5，k2=-0.543 6，b2=1.961 7。

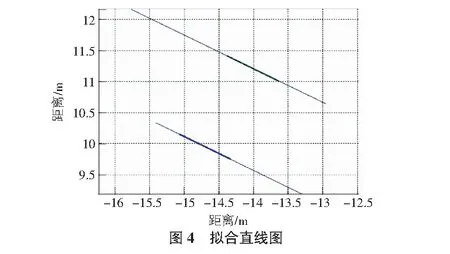
4 结语

将三维激光扫描技术应用到铁路工程，本文主要解决轨道点云的外业采集、处理与线形拟合问题。从原始轨道点云的数据采集和拼接出发，经过原始点云选取，又以每个点云高程为判别条件剔除无用数据，再经过滤波、精简等专业处理，最终获得轨道点云。对轨道点云采用最小二乘法进行线形拟合处理，得到既有线铁路轨道线形[10-12]。

本文实现直线轨道线形的提取，线形简单，后续可继续研究铁路更为复杂结构，如曲线，道岔等的提取；此外，后续研究中，可通过点云进行建模，检测轨道结构整体三维变形，为轨道受列车荷载变形研究及轨道维护提供支撑。