枣树修剪机械臂动态特性分析与性能试验

黄勇，张斌，王磊，付威，沈从举，尹成海,*

(1 石河子大学机械电气工程学院，新疆 石河子 832003；2 海南大学机电工程学院，海南 海口 570228；3 新疆农垦科学院，新疆 石河子 832000)

红枣是我国特色林果，其种植面积和产量均居世界首位[1]，2019年中国新疆红枣产量高达372.8万t[2]。目前，枣树修剪以人工修剪为主，存在劳动强度大、效率低、工作环境差、成本高等问题[3]。近年来，随着机器人技术、人工智能等领域的迅猛发展，使得利用机器人修剪代替人工成为可能。目前，机械臂动态特性研究已成为机器人研究的热点之一[4]。国内外学者对果园机械化修剪机器人动态特性进行了诸多研究，吴小锋[5]对林业修剪机器人进行了运动学、动力学仿真；唐果等[6]对高速公路绿篱修剪机器人运动特性研究，在ADAMS仿真软件中进行修剪机械臂刚性和柔性的动力学对比仿真，研究柔性因素对系统动力学特性的影响；李名地[7]对城市园林自动修剪机器人动力学仿真进行了研究，加入驱动智能控制，使得修剪机器人各关节协调运动良好；张斌等[8]设计了一种立体仿形修剪装置，可以实现枣树个体树形的立体分层仿圆柱形修剪，为红枣修剪机整机的设计提供了理论依据和技术支。

国内外研究者对机器人或机械臂动态特性进行了研究，明添等[9]研究排爆机器人五自由度操作臂动力学并进行动力学分析；TANAKA Y等[10]对六自由度并联机器人的动态力进行了分析，并提供了数值模拟结果；FIROOZABADI A E等[11]建立了具有3个柔性中间杆的3-RPR平面并联机器人的动力学模型，以研究中间杆柔性对末端执行器非期望振动的影响；王海等[12]对六自由度柔性关节机械臂的动力学分析，提出了六自由度的柔性关节机械臂的简化模型,利用拉格朗日方法建立其动力学方程；宛云龙[13]对机器人机械臂动力学进行了仿真研究，利用ODE对机器人机械臂动力学仿真；张东胜等[14]对五自由度混联机器人逆动力学分析，建立了并联机构的动力学模型；PEDRAMMEHR S等[15]利用MATLAB和ADAMS对机械手在给定运动场景下的运动学和动力学模型进行仿真；WU Y等[16]提出了一种新的五种自由式混合机器人，系统分析了其运动学和动力学。

目前，国内对于枣树修剪机械臂动态特性分析比较少，本文采用动力学分析与机械臂动态特性仿真分析对链式修剪机械臂进行模态分析和谐响应分析，并对样机进行性能试验，旨在为红枣修剪机器人的设计和优化提供了理论依据和技术支撑。

1 枣树修剪机械臂整机组成

枣树修剪机械臂为链式机械臂，由基座、基座旋转关节、机身、机身移动关节、肩关节、大臂、肘关节、小臂旋转关节、小臂等部分组成。基座旋转运动、机身移动关节、肩关节和肘关节的运动控制末端执行器的位置，小臂旋转关节的旋转运动控制末端执行器的姿态。通过基座旋转实现整机方位的调节，机身升降实现机械臂不同高度的调节，适应不同高度的枣树修剪作业。枣树修剪机械臂整机结构示意图如图1所示。

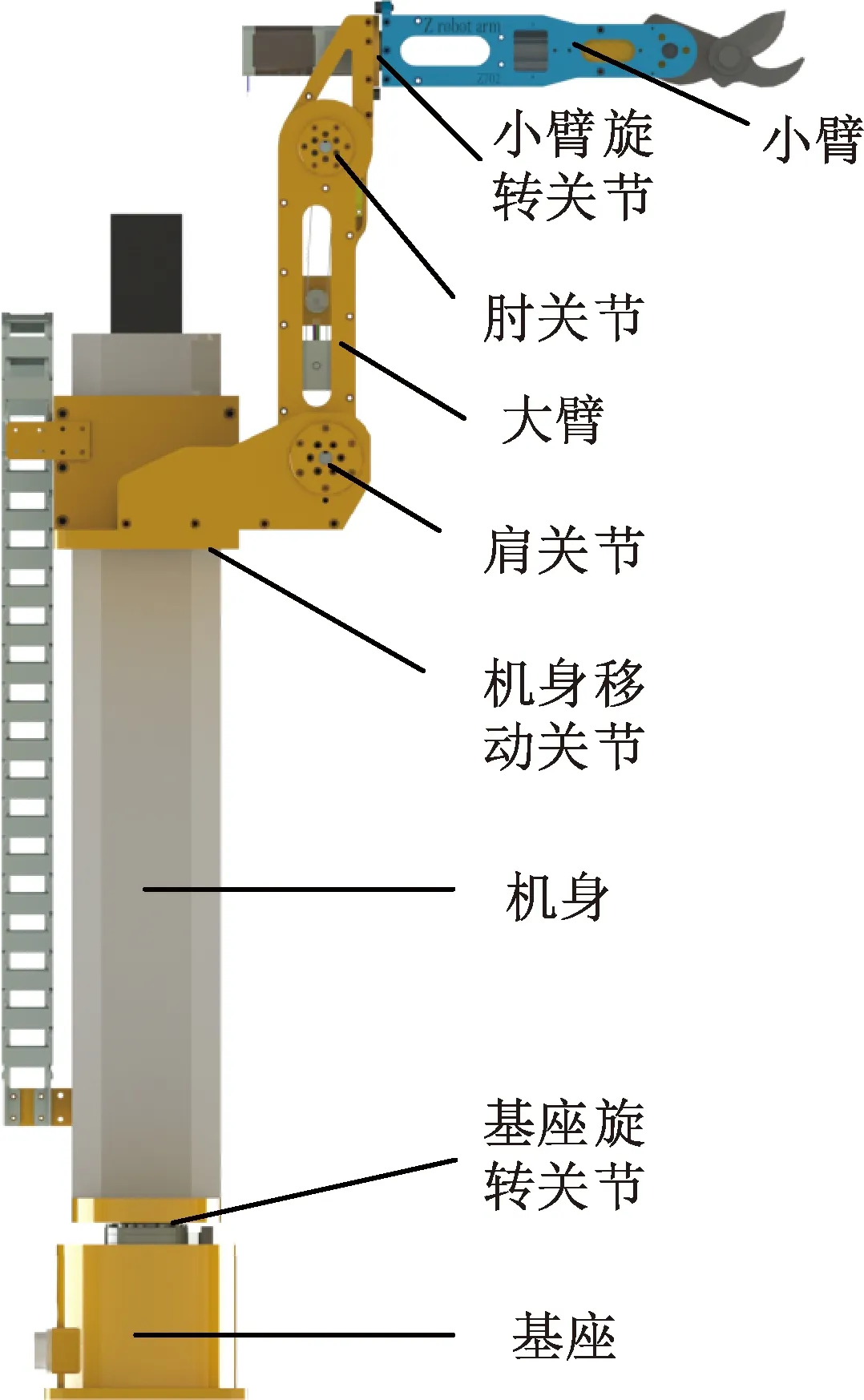
图1 机械臂结构示意图

2 机械臂动力学模型的建立

枣树修剪机械臂工作时，为使机械臂按照给定的轨迹运动，并满足各关节具体动作或修剪工作要求，应时刻输入相应的速度、加速度，这就需要动力源为枣树修剪机械臂各关节提供足够的驱动力/力矩，以保证机械臂各连杆和关节能够产生预期的速度、加速度。因此，为得到各关节产生的加速度/角加速度与关节输入力/力矩的关系，计算出各关节驱动的具体力/力矩值，机械臂动力学方程的建立是十分必要的[17]。

本研究参考文献[18]采用拉格朗日法动力学模型的推导。首先，定义拉格朗日函数为：

L=K-P，

(1)

式(1)中L为拉格朗日函数，K为系统动能，P为系统势能。

于是：

(2)

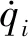
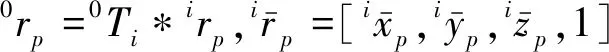
(3)

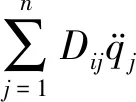
(4)

(5)

(6)

综上，依据枣树修剪机械臂本体结构参数，代入枣树修剪机械臂的运动方程(3)，确定机械臂各关节所需的最大力矩，结果见表1。

表1 机械臂各关节所需的最大力矩

3 机械臂动态特性仿真分析

机械臂在工作过程中产生振动或发生共振现象，将直接影响整机运动稳定性和末端定位精度，最终影响整机安全性和工作效率，为了使枣树修剪机械臂在工作中具有良好的动态特性，需要对设计的机械臂进行模态分析和谐响应分析。

3.1 有限元模型建立

利用Creo3.0按1∶1比例建立机械臂三维模型，将其保存为.x_t格式导入ANSYS有限元软件Workbench模块中，为了便于分析，删除了臂体上的小孔、倒角等对分析结果影响不大的特征。机械臂本体材料视为各向同性材料，机械臂主体材料采用6061铝合金加工而成，具体材料属性如下：材料为Al6061，密度为2.73×103kg/m3,泊松比为0.33，弹性模量为7×104MPa。

本文设计的机械臂主要针对枣树修剪作业，在实际修剪作业中由于对象复杂，拥有多个修剪位置，且每次修剪位置各不相同，因此，机械臂在工作过程中存在多种位姿状态，为了更准确分析机械臂动态特性，本文建立机械臂运动过程中的某一位姿和极限位姿两种状态下的机械臂有限元模型。对机械臂预处理，在满足计算精度的条件下进行网格划分，同时细化局部关节网格，单元类型选用solid45实体单元，该模型共划分191 551个单元，362 952个节点。机械臂在作业过程中各关节相互之间通过力矩作用协同动作，依据机械臂动力学理论分析结果对机械臂各关节施加边界条件，由表1设置各关节仿真模型的力矩参数。建立某一位姿下的机械臂有限元模型如图2所示。

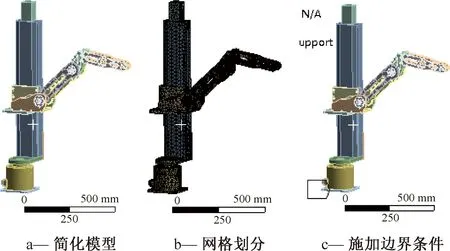
图2 机械臂有限元模型

3.2 模态分析

通过对机械臂运动位姿进行模态分析，机械臂五、六阶振幅相同，因此，本文主要研究机械臂前六阶模态，获得其固有频率与主振型，结果如表2所示，机械臂前六阶模态振型等效云图如图3所示。

表2 机械臂固有频率和主振型

图3 机械臂模态分析等效云图

由表2可知：机械臂前六阶固有频率在22.783～98.458 Hz之间，出现最大振幅的区域均位于机械臂小臂末端位置处。机械臂的一阶模态振动固有频率为22.786 Hz，最大振幅为15.494 mm，其一阶模态振型等效云图见图3a；二阶模态振动固有频率为30.225 Hz，最大振幅为12.863 mm，其二阶模态振型等效云图见图3b；三阶模态振动固有频率为34.52 Hz，最大振幅为57.36 mm，其三阶模态振型等效云图见图3c；四阶模态振动固有频率为72.091 Hz，最大振幅为55.739 mm，其四阶模态振型等效云图见图3d所示；五阶模态振动固有频率为98.458Hz，最大振幅为55.472 mm，其五阶模态振型等效云图见图3e；六阶模态振动固有频率为98.458 Hz，最大振幅为55.472 mm，其6阶模态振型等效云图见图3f。同理对机械臂运动过程中的位姿与极限位姿进行模态分析，机械臂极限位姿的前六阶固有频率在 19.605～94.317 Hz 之间，出现最大振幅的区域与机械臂运动过程中位姿状态一致，均位于机械臂小臂末端位置处。

通过对机械臂运动过程中的位姿与极限位姿进行模态分析，机械臂前六阶固有频率在 19.605～98.485 Hz 之间，振幅在 8.762～101.25 mm 之间变动，频率在 79.858 Hz 时振幅达到最大，最大振动区域位于机械臂小臂末端位置处。为避免机械臂工作过程产生共振导致故障问题，应避开机械臂固有频率范围。

3.3 谐响应分析

为探究设计的机械臂在工作时因克服共振以及抵抗疲劳等产生的受迫振动对枣树修剪机械臂结构造成不良影响[19]，需要对机械臂进行谐响应分析，研究机械臂固有频率在不同频段下机械臂位移-频率响应曲线。本研究根据机械手设计要求，机械臂末端负载不低于2 kg，在小臂末端连接孔内表面沿Z轴负方向添加20 N的作用力，设置谐响应分析频率范围为0 ～300 Hz，求解间隔为20。经求解，分别得到机械臂小臂末端在X方向、Y方向、Z方向的位移-频率响应曲线，如图4所示。

图4 机械臂小臂末端X(a)、Y(b)、Z(c)三个方向位移-频率响应曲线

由图4可见：机械臂固有频率在30 Hz时，小臂末端位置处沿X方向位移达到最大值1.468 8 mm(图4a)；机械臂固有频率在90 Hz时，小臂末端位置处沿Y方向位移达到最大值4.535 7 mm(图4b)；机械臂固有频率在75 Hz时，小臂末端位置处沿Z方向位移达到最大值3.523 7 mm(图4c)。对比分析可知：机械臂末端位置沿Y、Z方向的振动比X方向大，其中沿Y方向的影响最大。

上述对机械臂动态特性分析结果表明：该机械臂前六阶固有频率主要在19.605～98.458 Hz之间，最大振动区域位于机械臂小臂末端位置处，机械臂在低频下的受迫振动较明显，当固有频率为90 Hz时，小臂末端位置处沿Y方向位移达到最大值4.535 7 mm，易发生共振现象，因此，该机械臂在实际工作时应避开该振动频段。

4 样机性能试验

机械手在运动过程中有无明显冲击现象决定了机械手运动过程的平稳性性能，因此对机械手运动过程进行平稳性性能测试试验。

4.1 试验方案

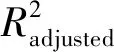
(7)

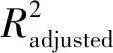
图5 机械手运动平稳性测试试验

4.2 试验结果及分析

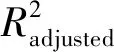
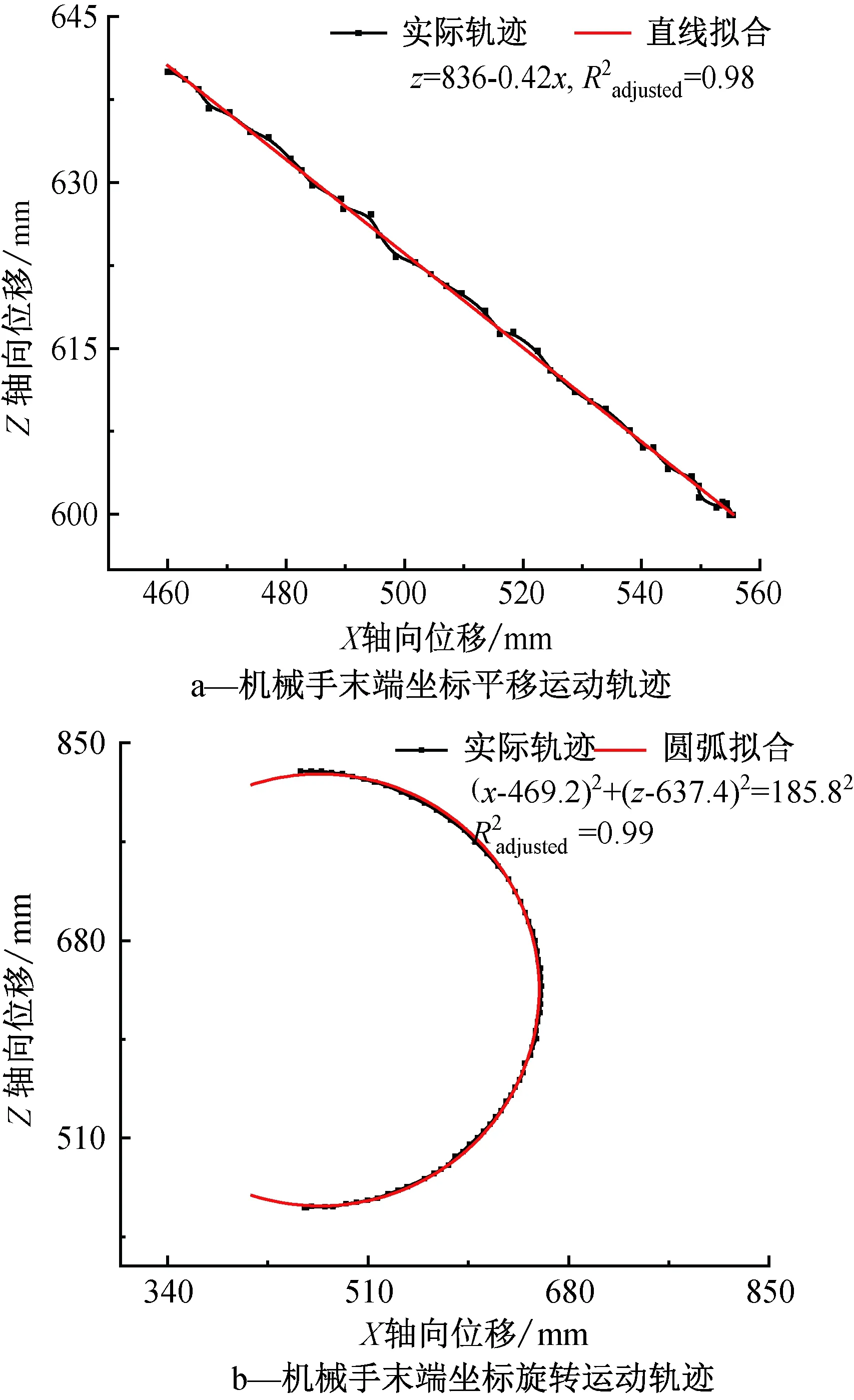
图6 机械手末端运动轨迹线

5 结论

(1)为避免机械臂工作过程产生共振导致故障问题，对机械臂位姿进行模态分析，机械臂前六阶固有频率在22.786～98.458 Hz之间，振幅在12.863～55.739 mm之间变动，得出频率在72.091 Hz时振幅达到最大，最大振动区域位于机械臂小臂末端位置处。因此，工作时应避开机械臂固有频率范围。

(2)对机械臂进行谐响应分析，当固有频率为90 Hz时，小臂末端位置处沿Y方向位移达到最大值4.535 7 mm，易发生共振现象，因此，该机械臂在实际工作时应避开该振动频段。