基于智能分数阶互补滑模的PMLSM直接推力控制
苗 雨,赵希梅
(沈阳工业大学 电气工程学院,沈阳 110870)
0 引 言
永磁直线同步电机(以下简称PMLSM)具有效率高、推力大、响应快等优点,近年来在航空航天、数控机床、机器人设备和半导体加工制造等领域得到了广泛应用[1-2]。直接推力控制(以下简称DTFC)是将旋转电机中的直接转矩控制延伸到直线电机上的一种控制策略[3]。DTFC直接对磁链和推力进行控制,与矢量控制相比结构更简单,速度响应更快,是轨道交通和运输领域的首选[4-5]。DTFC系统具有快速的响应和良好的鲁棒性,但由于其稳态误差和超调量较大,无法使系统的跟踪精度满足高性能要求[6]。因此,设计一种既可以保留DTFC快速响应的优点,又具有较小速度和推力脉动的控制器,使系统获得更好的跟踪性能,对实现PMLSM的高精度高速度控制具有重要意义。
近年来,国内外专家学者为提高PMLSM的控制性能,进行了大量的研究。滑模控制(以下简称SMC)具有广泛的应用,但由于其控制的不连续性,存在抖振问题,通常需要与其他方法结合才能达到更好的控制效果[7]。文献[8]提出了一种基于新型趋近律的SMC,能避免开关增益持续增大,该方法可在一定程度上削弱SMC的抖振问题,并提高DTFC系统的鲁棒性能,但系统仍存在较大的推力脉动。文献[9]设计了一种带有分数阶PIαDβ型滑模面用于永磁同步电动机调速系统,通过分数阶微积分算子特有的记忆特性和遗传特性抑制了抖振问题,但系统的动态响应能力较差。文献[10]提出了一种基于神经网络变阶次的积分滑模控制方法,该方法具有更加快速的动态响应速度,但选用传统的积分滑模面使系统仍存在较大的稳态误差。文献[11]在广义滑模面的基础上增加了一个互补滑模面,可以提高系统的位置跟踪精度,并降低不确定性对系统运行的不良影响,但SMC的抖振问题仍未得到较好的解决。文献[12]将互补滑模控制和智能控制中的迭代学习相结合,该方法能够有效抑制不确定性对系统的影响,从而加快控制器的收敛速度,提高收敛精度。
为使DTFC系统的速度跟踪能力得到进一步提高,本文设计了一种基于RBF神经网络的智能分数阶互补滑模控制(以下简称IFOCSMC)方法。首先,设计了分数阶广义滑模面和分数阶互补滑模面,分数阶微积分算子具有滤波特性和缓慢传递能量的特点,分数阶互补滑模面既可以削弱SMC的抖振问题,又能够减小DTFC的推力脉动,同时也增加了运算自由度,减小系统跟踪误差的同时,也有较强的抗干扰能力。其次,利用RBF神经网络对系统受到的扰动和未建模部分进行在线逼近,进一步提高系统的动态响应能力和抗干扰能力。仿真结果表明,该方法可以有效地加快系统的响应速度,减小稳态误差,系统速度跟踪性能得到明显的提高。
1 PMLSM数学模型
d-q坐标系下的PMLSM电压方程:
(1)
式中:ud,uq,id,iq,ψd,ψq分别为d,q轴电压、电流和和磁链;ωr为磁链矢量的角速度;Rs为动子电阻。
磁链矢量的角速度:
(2)
式中:p为极对数;τ为极距;v为动子机械速度。
磁链方程:
(3)
式中:Ld,Lq为d,q轴电感;ψf为永磁体磁链。
磁路对称时Ls=Ld=Lq,PMLSM的电磁推力表达式:
(4)
式中:Fe为电磁推力;ψs为定子磁链;δ为ψs和ψf的夹角;kf为电磁推力系数。
机械运动方程:
(5)
式中:M为动子质量;B为粘滞摩擦系数;F为系统所受扰动的负载力。
2 基于IFOCSMC的DTFC系统
PMLSM的DTFC系统结构框图如图1所示。
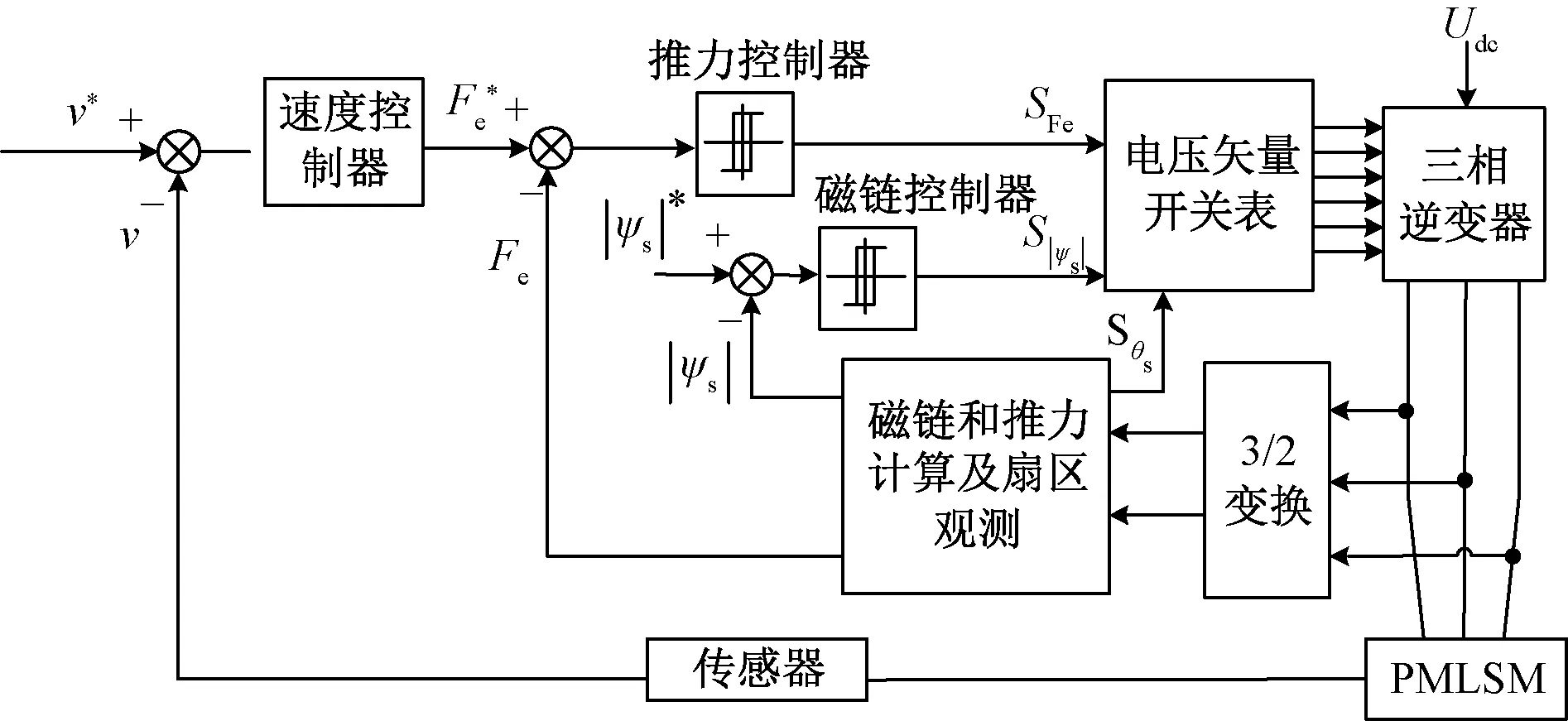
图1 PMLSM的DTFC系统框图
2.1 分数阶微积分
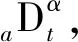
(6)
式中:a和t是积分算子的上下限;α为微分算子的阶次;R(α)是α的实部。当不涉及上下限问题时可简写为Dα。
RL型分数阶微积分定义:
(7)
式中:n取整数,且m-1<α
由于分数阶微积分的值无法得到精确数值解,故采用Oustaloup滤波器来逼近。设(wb,wh)为选定的拟合频率段,该滤波器的传递函数:
(8)
该滤波器的零极点和增益求解公式:
wk=wbwu(2k-1+α)/n
(9)
w′k=wbwu(2k-1-α)/n
(10)
K=whα
(11)

为提高滤波器在wh和wb边界附近的拟合效果,引入改进的Oustaloup滤波器:
(12)
式中:wk≈(bwh/d)(α+2k)/(2n+1),w′k≈(dwh/b)(α-2k)/(2n+1),加权参数b=10,d=9。

2.2 FOCSMC设计
当不考虑扰动即F=0时,电机的理想运动方程可改写:
(13)
式中:An=-B/M,Bn=Kf/M,u为控制器输出。
电机在实际运行时会受到不确定性的干扰,当考虑扰动即F≠0时,电机运动方程可改写:

Anv+Bnu+H
(14)
H=ΔAv+ΔBu+(Cn+ΔC)F
(15)
式中:Cn=-1/M;ΔA,ΔB和ΔC为M和B引起的扰动变化量;H为总扰动,H未知但有界。
互补滑模控制(以下简称CSMC)具有较强的鲁棒性,并且增加的互补滑模面能使系统具有更高的跟踪精度,分数阶互补滑模控制(以下简称FOCSMC)是在CSMC的基础上,将两个滑模面中的整数阶微积分替换为分数阶微积分,削弱抖振问题、减小推力脉动的同时,增加了运算自由度,能够进一步提高PMLSM控制系统的速度跟踪能力。
定义速度跟踪误差:
e=v*-v
(16)
式中:e为速度跟踪误差;v*和v分别为给定速度输入和实际速度输出。
FOCSMC的滑模面定义:
S=S1+S2
(17)
S1=Dαe+2λe+λ2D-αe
(18)
S2=Dαe-λ2D-αe
(19)
式中:Dα为分数阶微积分算子;α和λ都为正常数。
分别对式(18)和式(19)两边求取α阶导数,可得:
DαS1=D2αe+2λDαe+λ2e
(20)
DαS2=D2αe-λ2e
(21)
结合式(17)~式(19)可得:
S=S1+S2=2(Dαe+λe)
(22)
将式(22)与式(20)和式(21)联立可确定S1和S2的关系:
DαS1-DαS2=2λ(Dαe+λe)=λS
(23)
定义Lyapunov函数:
(24)
引理1:设x(t)∈Rn是一个可微函数的向量,对于t≥t0的任意时刻,以下关系成立[13]:
(25)
结合引理1和式(18)~式(21),求取式(24)的α阶导数可得:
DαV1≤S1DαS1+S2DαS2≤
S1DαS1+S2(DαS1-λS)=
S1DαS1+S2(DαS1-λS1-λS2)=
(S1+S2)(DαS1-λS2)=
S(D2αe+2λDαe+λ2e-λS2)=
2λDαe+λ2e-λS2]
(26)
FOCSMC的控制律u由等效控制ueq和切换控制usw两部分构成,FOCSMC的控制律表示:
u=ueq+usw
(27)
两部分分别设计:
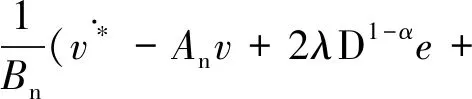
λ2D1-2αe+λD1-2αS1)=
(28)
(29)
式中:sat(·)为饱和函数;Φ>0为边界层厚度,具体表示:
(30)
由于传统的符号函数具有不连续控制的特性,故将符号函数替换为近似连续控制的饱和函数,可使SMC的抖振得到进一步削弱。将式(27)、式(28)和式(25)代入式(22)中,可以得到:
(31)
由式(31)可得该控制器满足Lyapunov稳定性定理。
2.3 IFOCSMC设计
系统运行时,干扰会对跟踪性能有不良影响。利用RBF神经网络在线逼近系统受到的扰动,对系统未建模部分进行补偿,进一步提高系统的控制性能。RBF神经网络结构简单,逼近能力强,可以避免局部最优的问题,并且具有较快的训练速度,结构如图2所示。
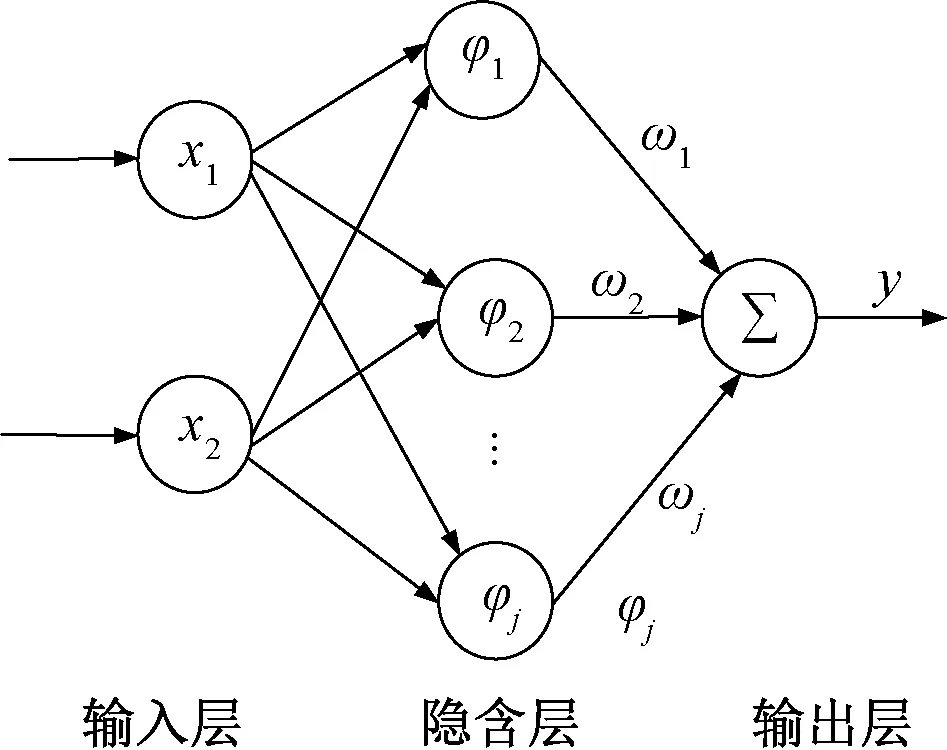
图2 RBF神经网络结构图
神经网络的输入为速度误差和误差的变化率,表示:
(32)
神经网络的激活函数为高斯函数,定义:
(33)
式中:ci为隐含层第i个节点函数的中心,σi为第i个隐含层节点函数的基宽参数。
神经网络的输出为每个隐含层神经元的输出值与对应的连接权重的加权之和,表示:
(34)
式中:n为隐含层节点的数量;ωi为连接权值。
定义RBF神经网络的输出:
uR=WTφ
(35)
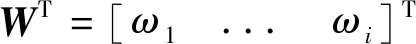
神经网络权重调整的自适应律:
W=-η(S1+S2)φ
(36)
式中:η为神经网络权重自适应系数。
RBF神经网络的输出存在一个理想的最优值:
uR*=W*Tφ+ε
(37)

IFOCSMC的结构如图3所示。系统总控制律可写成:
u=ueq+usw+uR
(38)
定义Lyapunov函数:
(39)
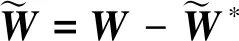
结合式(36)和式(38)可得:
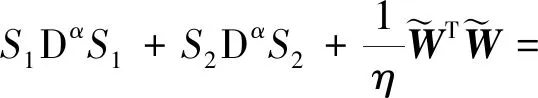
(40)
由式(40)可得,IFOCSMC方法满足Lyapunov稳定性判据。
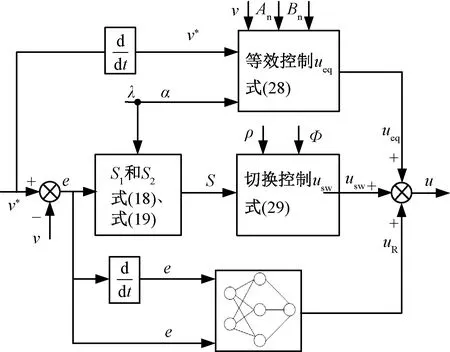
图3 IFOCSMC原理框图
3 仿真结果分析
为了证明本文方法的有效性,对基于IFOCSMC的PMLSM DTFC系统进行仿真分析,并与使用CSMC和FOCSMC的系统仿真运行结果进行对比。选用的PMLSM参数:M=16.4 kg,τ=32 mm,Rs=2.1 Ω,ψf=0.09 Wb,B=8.0 N·s/m,p=3,Ld=Lq=27 mH。IFOCSMC的参数:ρ=12,η=0.5,α=0.24,λ=95,Φ=0.002,CSMC和FOCSMC的参数与IFOCSMC一致。
电机空载起动,在0时输入幅值±600 mm/s的1.2 Hz方波信号作为速度给定信号,并在电机动子上施加如图4所示的非周期性变化扰动。图5为三种方法的速度响应曲线。从图5可以看出,采用CSMC方法时,当输入速度指令后,系统首次到达给定速度并稳定运行的时间约为0.08 s,速度超调较大,约为给定速度的6.8%,在1.3 s动子受到较大的负载扰动时,稳定运行速度有52 mm/s的下降,整体速度曲线存在明显抖振,并且在负载增大时抖振问题更加严重。采用FOCSMC方法时,系统开始稳定运行的时间约为0.06 s,超调量和抖振都有明显减小,受到负载扰动时,运行速度下降18 mm/s。采用IFOCSMC方法时,系统开始稳定运行的时间约为0.03 s,基本无超调和抖振,并且当动子受到负载扰动时速度曲线基本无波动。

图4 非周期性扰动曲线
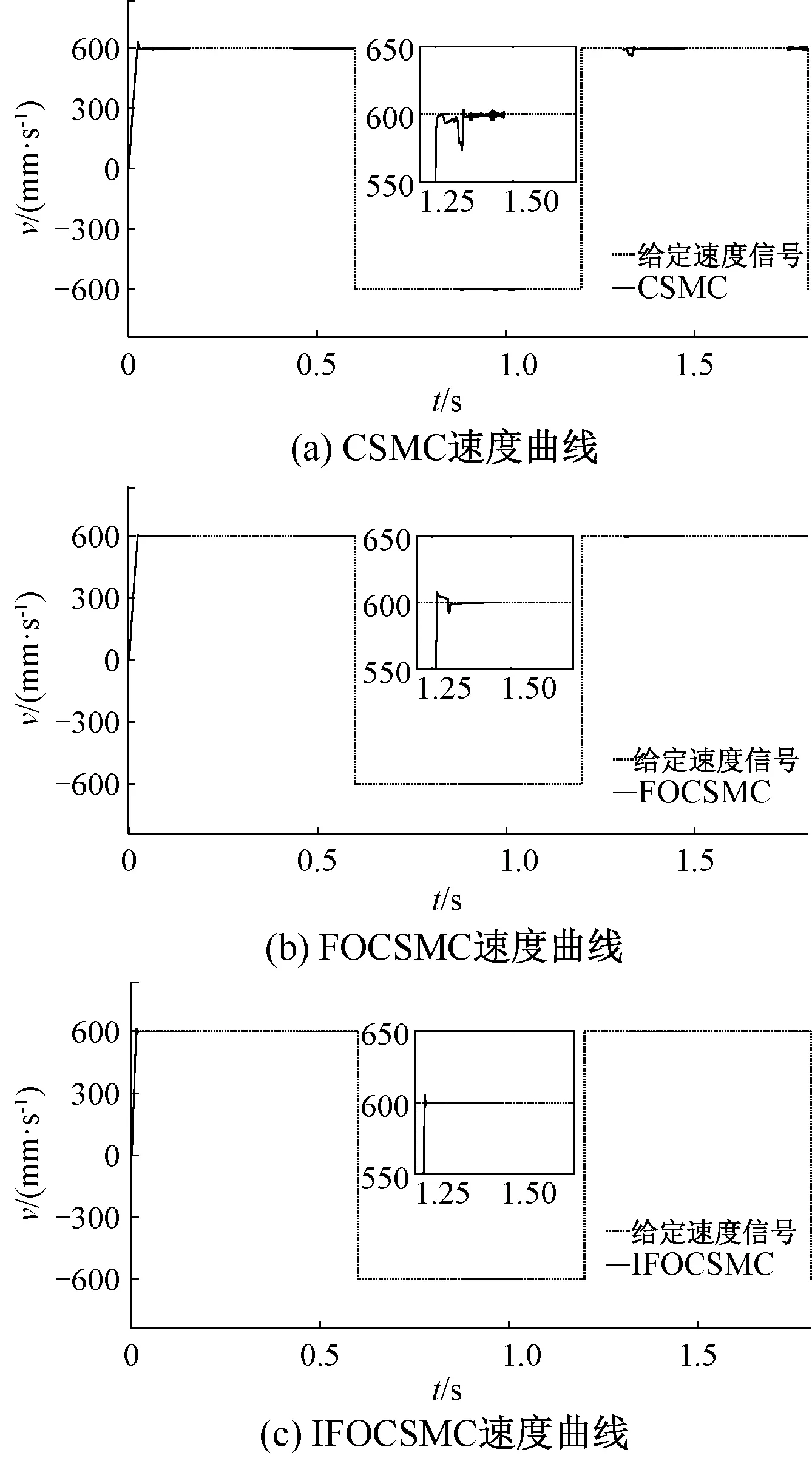
图5 三种方法的系统速度响应曲线
图6为三种方法的速度误差曲线。从图6可以看出,当电机稳定运行时,CSMC方法的系统速度跟踪误差范围为-4 mm/s~11.8 mm/s,约为给定速度的1.3%。FOCSMC方法的误差范围为-1.8 mm/s~5.6 mm/s,约为给定速度的0.6%。IFOCSMC方法的误差范围为-1.2 mm/s~2.4 mm/s,约为给定速度的0.3%,与前两种方法相比有明显减小。对比速度跟踪误差曲线可知,当稳定运行时,IFOCSMC方法速度跟踪误差更小并且控制更加平滑。
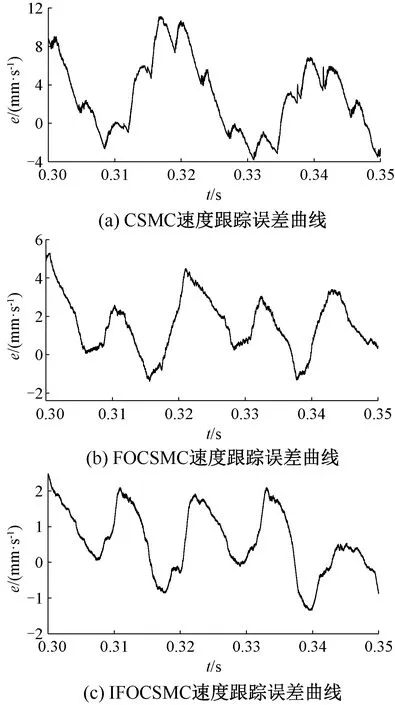
图6 三种方法的系统速度跟踪误差曲线
图7为三种方法的电磁推力曲线。从图7可以看出,在给定速度指令突变时,IFOCSMC方法的瞬间最大电磁推力较CSMC方法和FOCSMC方法相比有明显增大,更大的电磁推力可使系统迅速作出响应,到达稳态后IFOCSMC方法的推力脉动也较小。
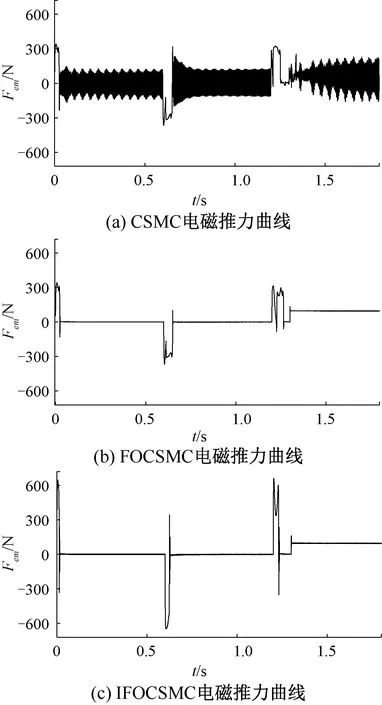
图7 三种方法的系统电磁推力曲线
图8为两种方法第一次到达稳态时滑模函数的轨迹。与FOCSMC方法对比可以看出,IFOCSMC方法的滑模曲线能够提前约0.03 s收敛到稳态,说明该方法能够加快系统的跟踪速度。

图8 两种方法的滑模收敛曲线
通过上述仿真运行结果的对比可以看出,IFOCSMC方法能够有效抑制抖振,减小推力脉动,使系统在抗干扰能力和速度跟踪性能上都更为出色。
4 结 语
为提高PMLSM的DTFC系统的速度跟踪能力,本文设计了一种基于RBF神经网络的IFOCSMC方法。该方法利用分数阶互补滑模面削弱抖振并抑制推力脉动,减小了系统的稳态误差。利用RBF神经网络对扰动进行补偿,进一步加快了系统的跟踪速度并提高抗干扰能力。仿真结果表明,该方法能使系统具有更快的动态响应速度、更小的稳态误差,系统的抗干扰能力和速度跟踪能力得到了明显的提高。

