电机碳刷导线结构对碳刷强度的影响

周唯儒，阳胜利

(捷和电机制品(深圳)有限公司，深圳 518104)

0 引 言

电机碳刷是电动机碳刷和发电机碳刷的统称。电机碳刷顶上有导线引出，体积有大有小。电机碳刷中包括了碳刷、铜线、碳刷套以及碳刷铜套，碳刷通过弹簧提供的弹力保证与换向器的接触。为了防止碳刷与换向器之间的接触不良，导致火花或者动力不平稳，通常弹簧弹力要保持一个较高的值，以保证碳刷有足够的力顶在换向器上。

有刷直流电机结构简单、控制方便[1]，以低成本、输出大转矩、能够频繁开关机及正反转调节方便的优势，被广泛应用特别在一些恶劣的环境中，碳刷作为直接影响电机能否正常运转及电机工作寿命的关键件[2]，在电机使用中起到了非常关键的作用。在生产装配中，保证电机碳刷的结构强度以及完整装配到电机上显得尤为重要。如果电机碳刷在生产中就已经损坏，装配到电机上后，整个电机就会因为碳刷无法工作，导致电机的失效，造成了资源的浪费。

在实际的生产过程中，碳刷装配后，发现个别碳刷与铜线之间的连接发生了材料断裂，导致碳刷无法使用。本文对此进行了理论分析、计算及实验，结果表明，碳刷的失效是由碳刷弹出瞬间的冲击力过大而导致的，与实际情况相符；提出了改进措施，通过仿真分析了不同铜线结构对碳刷强度的影响。本文的研究为碳刷的结构设计提供了可以借鉴的依据。

1 碳刷结构和实验

1.1 碳刷几何模型

本文采用的模型是捷和电机制品(深圳)有限公司碳刷产品，如图1(a) 所示，碳刷结构如图1(b)所示，由碳刷、铜套、碳刷壳体、弹簧组成。图1(b)中，弹簧用于提供碳刷弹出的弹力，且保持一个预紧力，碳刷铜套用于提供支撑。

图1 碳刷实物及几何模型

1.2 拉断实验测试

为了判断碳刷破坏的拉力大小，进行碳刷的破坏实验。通过对碳刷进行极限拉伸实验，测量碳刷的最大拉力值，从而确定是否因为瞬间弹力过大导致碳刷破坏。将碳刷放置在工作台上用拉力计拉碳刷，固定碳刷铜片一端，拉动拉力计并查看拉力计读数，如图2所示。缓慢拉动直到拉断为止。对24个碳刷进行拉力极限测试，1～12样本数据为1组测试数据，13～24样本为2组测试数据。样本来源于供应商提供样本的随机采样，测试结果如表1所示。拉断后的碳刷如图3所示，断口主要集中在铜线和碳刷连接部位。整理数据后可以得到，1组的碳刷的拉断力在25～45 N之间，其中在30～40 N之间的数据为6个，占到整体数据的50%，最大可以承受45 N的拉力；2组的碳刷拉断力在36～48.5 N之间，其中在30～40 N之间的数据为2个，占到整体数据的16.67%，最大可以承受48.5 N的拉力，且拉断时铜线并未损坏，石墨碳刷部分先失效破坏。

图2 拉力计拉断碳刷实验

图3 碳刷断口

表1 拉断力与实验样本

1.3 理论计算

理论计算首先用胡克定理进行弹簧的弹力计算，公式如下：

F=Kx

(1)

式中：F为弹力；K为弹簧的劲度系数；x为弹簧的压缩量。

经过测量，弹簧的压缩量x=36 mm，劲度系数K=0.011 6 kg/mm,如图4所示。根据式(1)计算，F=4.176 N。

此弹力为碳刷中的弹簧由压缩到释放到36 mm时的最大弹力。

图4 弹簧的劲度系数测量

碳刷加速度计算应用牛顿第二定律，公式如下：

F=ma

(2)

式中：F为力；m为质量；a为加速度。

经过测量，碳刷的质量m=0.004 kg，根据式(2)的计算，a=1 044 m/s2。

碳刷弹出到碳刷壳体边缘，完全弹出，末速度计算符合式(3)，计算末速度为6.13 m/s。

(3)

1.4 运动实验测试

为了捕捉记录碳刷弹出的整个运动过程以及弹出时间，应用高速摄相机对碳刷进行拍摄记录。实验采用千眼狼高速相机，由三人配合完成，分别负责补光、释放碳刷、记录，拍摄的视频数据直接由记录仪传至电脑保存。图5为操作界面。采集后的时刻及位置如图6所示，碳刷运动到最大行程位置如图7所示。通过右上角的时间戳可以得出，碳刷在初始位置的时间为90.064 ms，运动完全弹出的时间为100.075 ms，运动弹出所用时间为10.011 ms。根据式(4)：

(4)

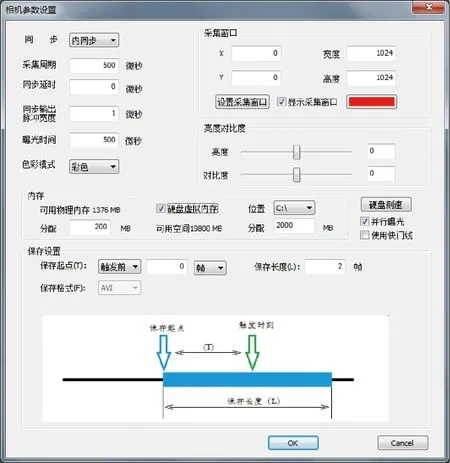
图5 高速摄相机操作界面

图6 碳刷压缩的初始位置

图7 碳刷释放后的位置

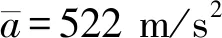
理论计算的末速度为6.13 m/s,与实际测试计算的末速度v末real=4.99 m/s相差1.14 m/s，误差为18.597%。

根据图8，从运动突然停止，可以得到碳刷在最大速度后到停止所用的时间，为1 ms。根据图9的运动轨迹，在下一帧后，碳刷开始回弹。该数据用于后续在仿真软件中设置时间。

图8 碳刷完全停止

图9 碳刷开始回弹缩回

2 有限元方法

采用有限元法对结构受力开展分析，常用的有两种分析方法：静力学分析和动力学分析。ANSYS Workbench软件中的static structure模块和explicit dynamic模块分别对应模拟静力过程和动力过程的分析。静力分析通常用来求解静态或准静态分析过程，可以得到精确力学响应，然而在处理冲击、碰撞、爆炸等问题时，显示动力学更适合。显示动力学分析用来确定结构因受到应力波传播影响、冲击或快速变化的时变载荷作用产生的动力学响应[3]。ANSYS Workbench中的explicit dynamic模块可以提供速度从1 m/s到5 000 m/s的计算[4]，根据实验计算的结果，弹出的速度在4.99 m/s。在ANSYS中显示动力学的计算流程如图10所示。

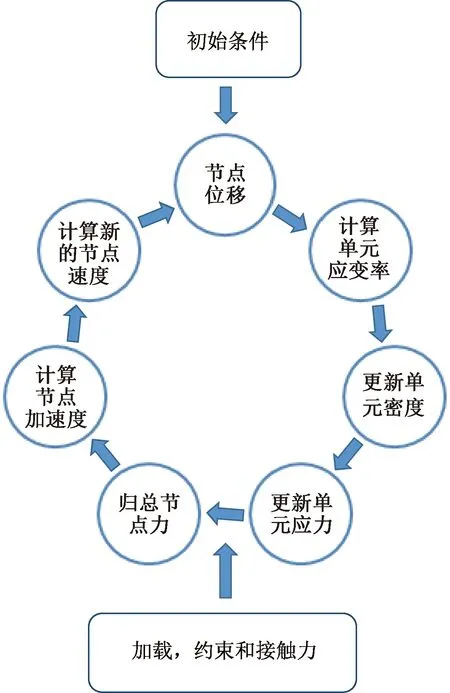
图10 显示动力学计算流程

2.1 材料属性

碳刷主要是由92%的石墨粉组成。石墨是碳的一种同素异形体，为灰黑色、不透明固体，化学性质稳定，耐腐蚀，同酸、碱等药剂不易发生反应。本文中将碳刷简化为铜线和碳刷结构进行分析，把弹簧弹力转化为碳刷弹出的速度，铜线拉直达到最大长度进行简化模型。铜线和碳刷的材料属性如表2 所示[5-6]。

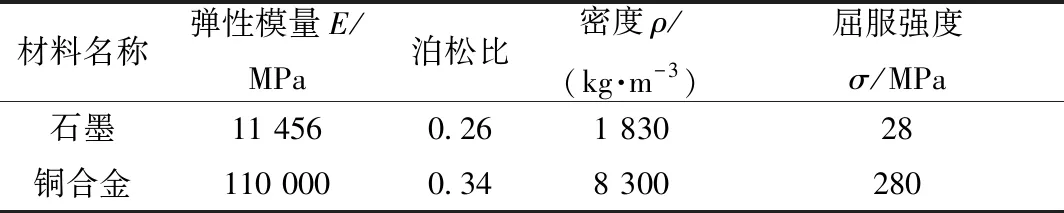
表2 材料属性

2.2 模型建立

碳刷模型在ANSYS 的Space Claim 2021 R1中建立，而后导入到explicit dynamic 模块进行材料赋予、网格划分、加载、约束等进行相关力学分析。本文建立两种模型进行分析。第一种为单根实心铜线，直径D=1.1 mm；第二种为多股铜线缠绕模型，最大直径与第一种方案相同，单根细铜线直径d=0.36 mm，如图11所示。

图11 简化碳刷结构

在保证模型网格质量的前提下，为了取得精确的结果并节省计算时间，本文取铜线处的单元尺寸为0.05 mm，旋转铜线的轴向方向取900切割。划分六面体单元网格。划分后铜线的单根网格质量在0.7～0.9之间，满足网格质量要求。单铜线模型单元数量为929 802，节点为984 910，多股铜线模型单元数量为910 002，节点为1 009 237，进行模拟计算分析两种模型。网格及网格质量如图12所示。

图12 网格及网格质量

2.3 边界条件与加载

为了分析计算整个弹出过程中铜线和碳刷连接处的拉力以及应力情况，首先确定计算的循环次数，为了确保解决方案的稳定性和准确性，明确时间集成中使用的时间步骤的大小受 CFL条件限制[7]。此条件意味着应力波不能在单个时间步骤中比网格中最小的特征元素尺寸走得更远。因此，解决方案稳定性的时间步骤标准:

(5)

式中：Δt为时间增量；f为稳定时间步因子(ANSYS 中默认为0.9)；h为单元特征长度；c为声音在材料中的传播速度。

由式(5)可以得出，确保稳定的时间步长是由网格中最小尺寸的单元决定的，网格划分小，将导致计算量变大。由于计算机硬件的限制，在相同计算机配置的前提下，尽量少的网格数量可以减少计算时间，但要保证网格的质量，过小的网格数量也会导致网格质量较差，从而计算的结果较为粗糙。根据式(5)计算，Δt≤9.00×10-9s, 计算拉住瞬间时间为0.001 s，将需要1.11×105个时间增量步。同理，可以计算单根铜线模型的时间增量步。

根据碳刷的实际结构，碳刷的铜片是固定约束，用来限制铜线的一端位移。多股铜线模型中每根铜线模型的接触方式为无摩擦接触，如图13所示。碳刷与铜线连接处为最外圈铜线与碳刷绑定接触，用来模拟实际的粘结情况。对碳刷施加初速度为4.99 m/s，速度方向为沿着Z轴负方向，对模型进行仿真计算。

图13 多股铜线碳刷仿真模型

3 结果与讨论

3.1 能量

在整个弹出过程中，碳刷弹出是先由速度最大值开始减速，此时系统的动能转化为内能，速度降低，而后内能减少，释放转化为动能，速度增加。当系统中动能转化为内能时，碳刷速度降低为0，以多股铜线模型为例，此过程如图14所示。

(2)在桩体贯入时,桩-土界面土体位移的规律可分为初始阶段和稳定阶段.初始阶段桩侧摩阻力占主导,在桩侧摩阻力作用下桩-土界面土体竖向位移急剧增大,方向与桩体贯入方向一致.但在较短时间内桩-土界面土体竖向位移迅速减小,随后进入稳定阶段.在稳定阶段,土体颗粒间相互作用力超过桩侧摩阻力,使桩-土界面土体位移在0 mm附近波动.

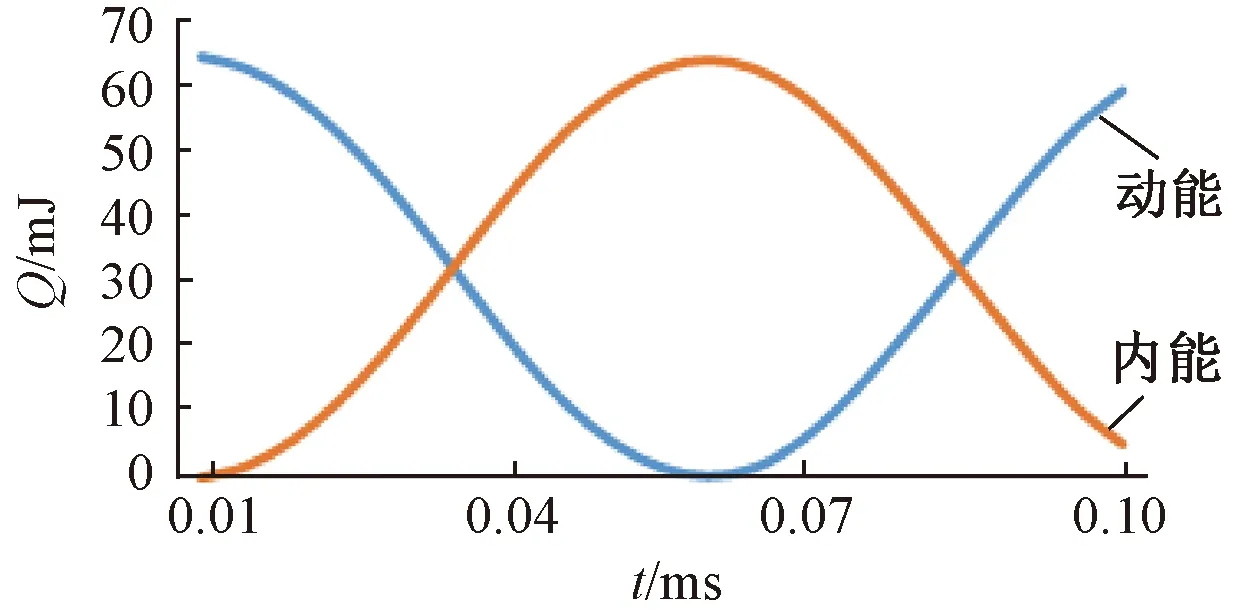
图14 弹出过程中内能和动能的转化

在弹出过程中，两种模型的动能变化规律一致，都是先由最大值减小，而后再升高。本文只取动能为0的时刻进行分析。对于单根铜线模型，动能为0的时刻为序号10对应的时刻；对于多股铜线模型，动能为0的时刻为序号12对应的时刻，数据如表3所示。整理表3得到如图15所示的趋势图。从图15可以得到，单根铜线结构的动能降低得较快。

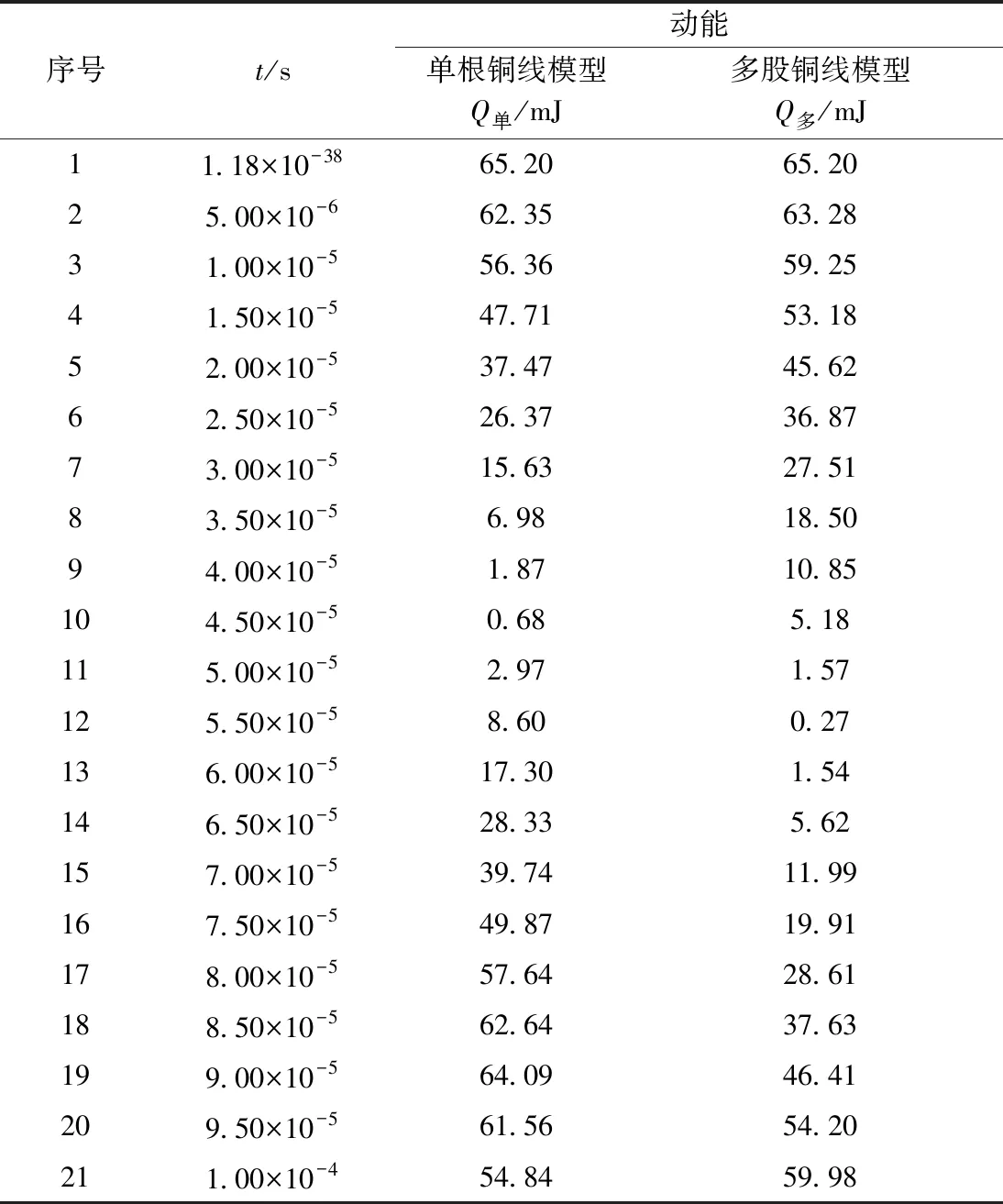
表3 弹出过程两种模型的动能

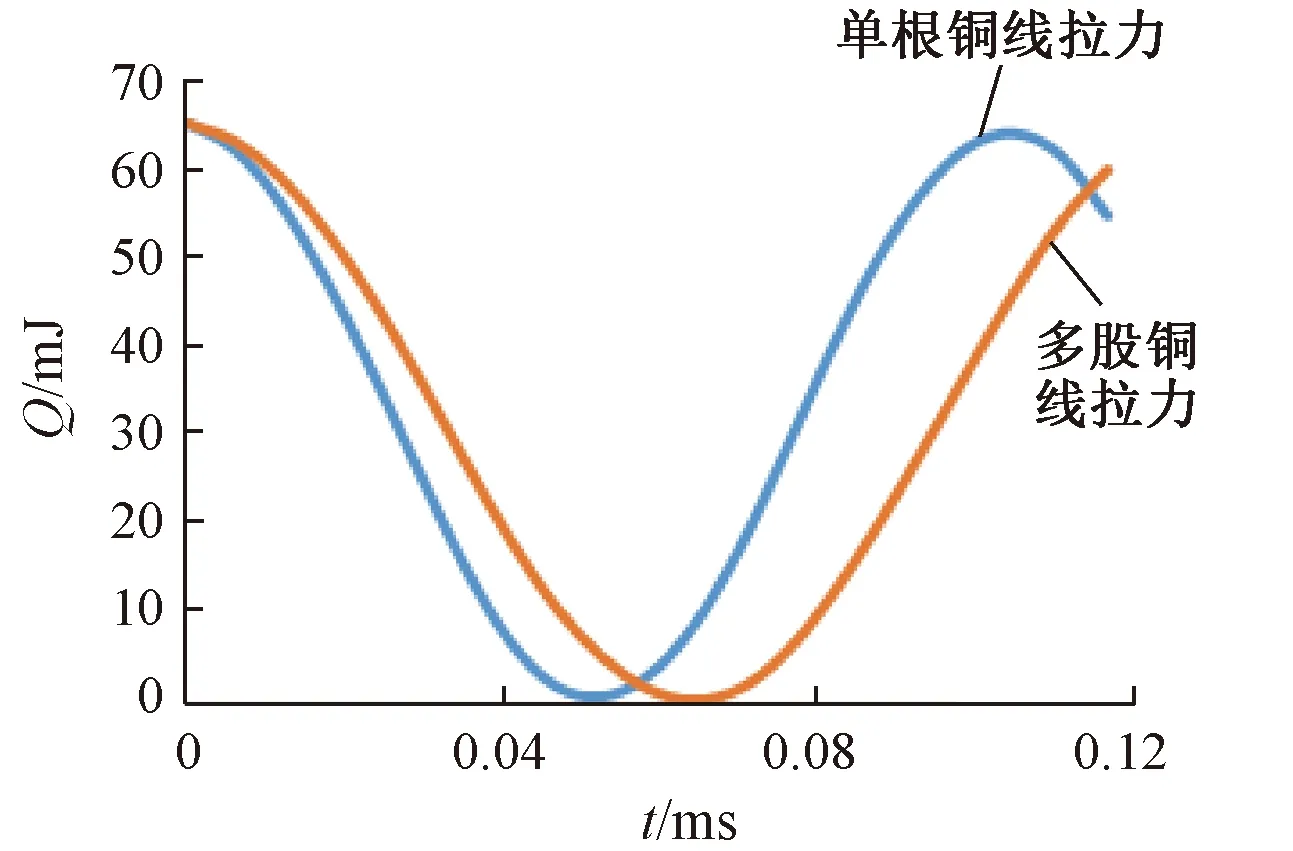
图15 动能对比图

计算过程中沙漏能的大小和相对量、绝对量可以作为计算结果精度的评价依据之一。一般认为沙漏能量不超过内能的10%，计算结果是可以接受的[8]。沙漏模式是一种非物理的零能变形模式，产生零应变和零应力，如不控制沙漏问题，则会产生严重的数值振荡现象。沙漏控制主要有两种方法：刚度控制和粘性阻尼控制[9]；同时，网格密度、网格质量单元类型等也可以进行沙漏控制[10-11]，本文使用网格质量方法来控制沙漏问题。计算过程中的沙漏能和内能列在表4中，比值均未超过10%。

表4 沙漏能与内能比值

3.2 铜线的拉力

在整个弹出过程中，碳刷弹出是先由速度最大值开始减速，当速度降低为0时，开始反方向运动，如此反复运动，直到能量消耗完毕。此过程中，碳刷一直受到铜线的拉力，从而降低速度直到减低到0。铜线的拉力呈现的趋势为，拉力开始逐渐增大，当拉力达到最大值后，拉力呈现下降趋势。整理计算结果如表5所示。整理表5数据如图16所示，可以得到拉力的变化趋势。

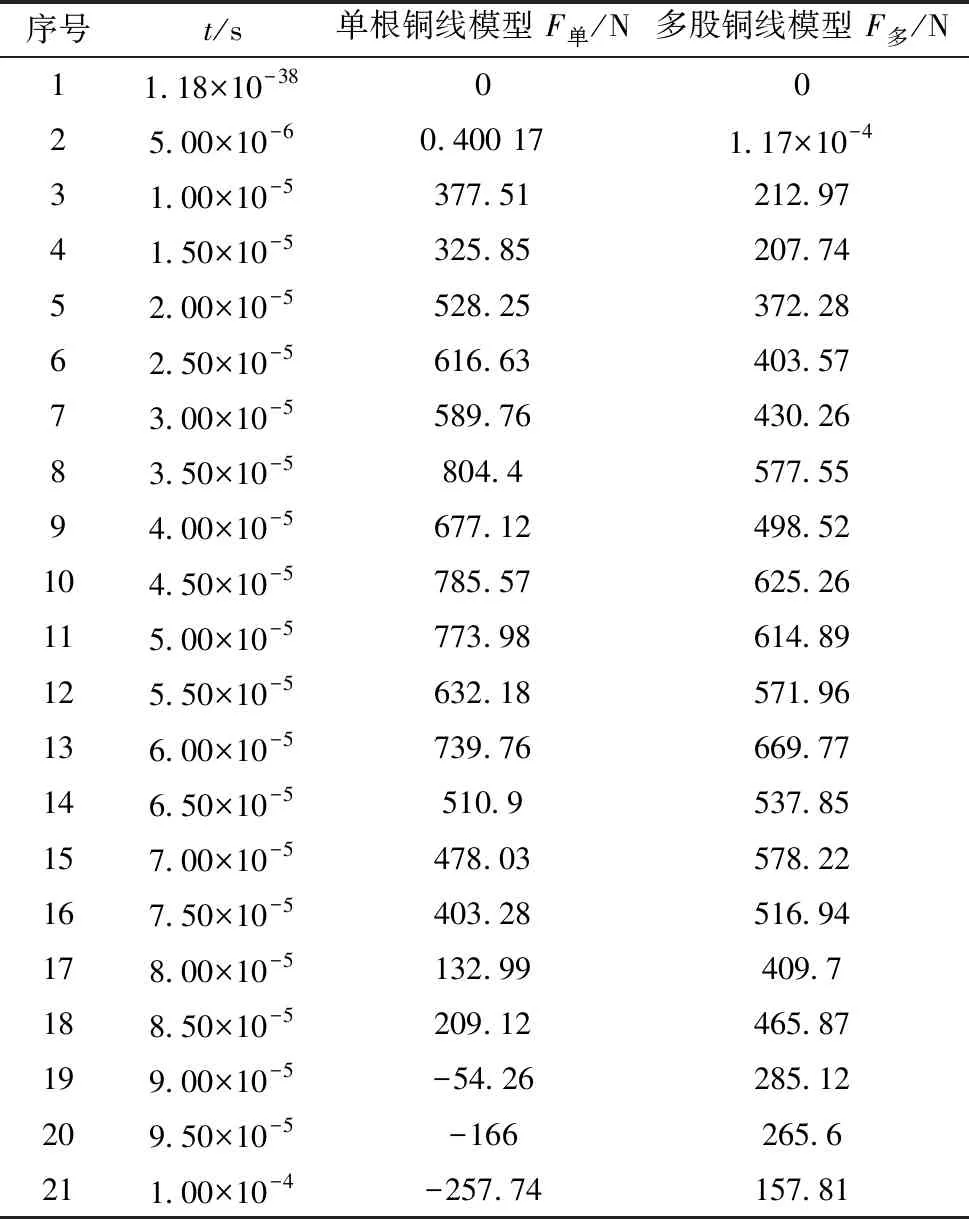
表5 弹出过程两种模型的拉力

图16 铜线拉力对比

对于单根铜线模型，动能为0的时刻为序号10对应的时刻；对于多股铜线模型，动能为0的时刻为序号12对应的时刻。此时，多股铜线的拉力明显小于单根铜线的拉力。

速度为0时的两种模型拉力比较如表6所示。

表6 速度为0时两种模型的拉力

3.3 石墨碳刷的应力

在实验测试时，并未发生铜线断裂的情况，并且铜线的屈服强度要远远大于石墨碳刷的屈服强度。本文只关注实际测试中破坏的碳刷结构的应力情况。碳刷与铜线连接部位的连接孔应力较大，已经超过屈服极限，如图17～图18所示。对于两种结构，碳刷的应力分布都集中在连接孔附近。多股铜线连接结构应力最大值较大，且在连接处接近外孔位置，最大为131.2 MPa，远超过屈服强度，但是总体应力分布在28～63.135 MPa范围的区域较单根铜线结构较小。单根铜线在碳刷圆柱凸台位置的应力均超过屈服强度，将会产生通透性的断裂。

图17 单根铜线碳刷应力分布

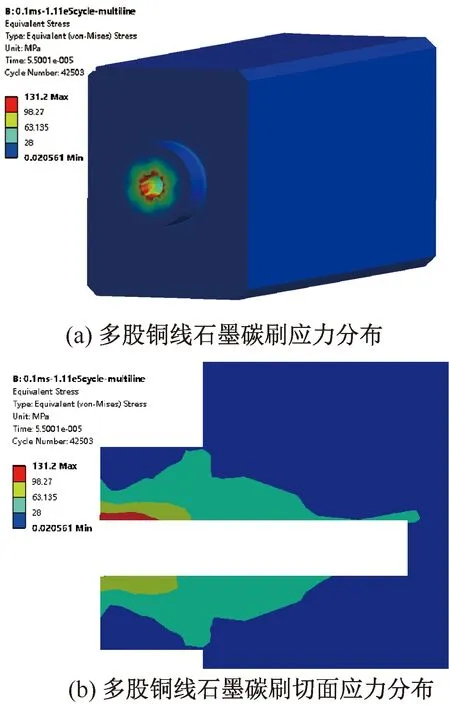
图18 多股铜线碳刷应力分布

3.4 石墨碳刷的应变

石墨的断裂应变范围在0.15%～0.226%[12]，对两种铜线结构的应变结果进行对比，单铜线结构的碳刷连接头部会发生失效。其失效方式为沿着红色区域开始全部断裂，这与实验中的情况相符，如图19(c)所示，此时最大应变达到了0.9%，且大部分区域都失效，如图19(b)所示。而多股铜线结构在外口位置有较大的应变，仅仅有一小部分，如图20(b)所示，已经超过了材料能承受的范围，发生失效，但是失效情况仅在外口局部位置，此时最大应变值为0.295%。它与单根铜线的最大应变值对比，相差接近3倍。

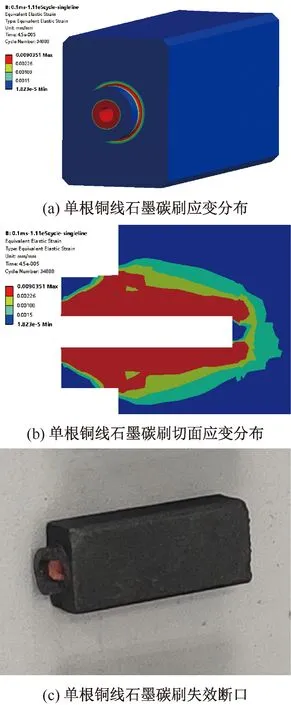
图19 单根铜线碳刷应变分布及实际断口

图20 多股铜线碳刷应变分布及实际断口

4 结 语

碳刷弹出并非理想情况，与理论计算中的速度值和加速度值有一定差异，但差异不大，这是由于碳刷弹出过程实际受到了铜套摩擦力的作用导致。

多股铜线结构可以缓冲一定的拉力，在碳刷弹出的时候，多股铜线的拉力要小于单根铜线的拉力。也就是说，在相同的弹簧作用下，多股铜线结构会更加坚固。

碳刷弹出的过程并非直接速度降低为零而停止，在这个过程中，会反复振荡，动能与内能相互转化，直到能量耗散完，系统停止。速度为零的时候，内能最大。

在弹簧相同的情况下，横截面积相同的多股铜线结构导致的碳刷失效面积要明显小于单根铜线结构。在一定程度上，多股铜线结构的设计要优于单根铜线设计。

本文的研究结果对碳刷结构设计有参考价值，辅助设计工程师进行不同情况下的碳刷设计，并为今后开发新的产品提供理论依据以及开发流程参考。碳刷的优化设计，是减少电机故障以及降低生产不良率的有效探索。