具有弹性约束和初挠度的弹性压杆力与位移关系分析
翟传鹏,何芝仙
(安徽工程大学 力学重点实验室,安徽 芜湖 241000)
桁架的优点是杆件主要承受拉力或压力,可以充分发挥材料的作用,节约材料,减轻结构重量。另外,桁架结构布置灵活,应用范围非常广,常用于大跨度的厂房、展览馆、体育馆和桥梁等公共建筑中。但是,由于桁架结构中受压杆件往往更容易发生失稳,所以,受压桁杆对桁架结构的承载能力起决定性的作用。实际工况中,桁架大多是通过直杆与连接板焊接或螺栓连接而成的,连接板对受压杆件具有一定的约束作用;另外,由于制造误差以及运输、安装过程中操作不规范,可能会导致实际使用的压杆存在一定的初挠度。因此,研究弹性压杆力与位移的关系,可为准确预测桁架结构的承载能力,特别是为破坏过程的力学行为分析提供前提条件。
1 力学模型和数学模型
实际工况中,桁架是由桁杆在两端与连接板焊接或螺栓连接而成的。因此,实际桁架中受压的桁杆可以视为受轴向荷载作用的具有弹性约束和初挠度的弹性压杆,其力学模型如图1所示。其中,弹性压杆两端弹性约束的支承刚度分别为K1和K2。由于制造误差以及运输、安装过程中操作不规范,可能会导致实际使用的压杆存在一定的初挠度。一般而言,初挠度是一个连续函数,为简化起见,假设初挠度为一个半波正弦函数[16],其中心位置挠度最大,即

图1 力学模型图
(1)
式中,ye为任意位置的初挠度值;e为最大初挠度;L为弹性压杆杆长;x为压杆截面位置。
对弹性压杆的整体平衡和局部平衡分别进行分析,其受力简图如图2、3所示。整体平衡:

图2 整体平衡受力简图图3 局部平衡受力简图
(2)
局部平衡:
∑M=0,M(x)=-FAxy+FAyx+K1θA,
(3)
式中,y为任意位置x截面的挠度值,y=y1+ye,其中y1为轴向荷载引起的挠度值;FAx、FAy为支座A处x、y方向的约束反力;FBx、FBy为支座B处x、y方向的约束反力;K1、K2为支座A、B处的支承刚度,定义为使支座产生单位转角需要施加的力矩;θA、θB为支座A、B处的转角;M(x)为任意位置x截面的弯矩。
(4)
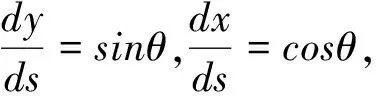
(5)
因铰支座的约束作用,在轴向荷载作用下,弹性压杆挠曲变形时压杆两端节点始终位于X轴线上,因此,两端节点的挠度值始终为0(即y=0)。所以,该方程应满足的边界条件为
近年来,微藻基因工程育种也取得了许多进展。微拟球藻(Nannochloropsis sp.)进化历史复杂,基因序列可用于多个物种,已经产生了许多转录数据集,常作为基因组学的研究模型[10]。研究表明,苹果酸酶是丙酮酸代谢和固碳的关键酶。三角褐指藻中苹果酸酶的过度表达可以在不影响生物量的同时显著提高油脂积累量[11]。虽然基因工程技术已逐渐成熟,但在微藻中的应用还较少。未来还应多从微藻代谢途径等角度出发,加深对微藻微观水平的认识,以便将基因工程技术更好地运用于微藻育种。
s=0,y=0;s=L,y=0。
(6)
2 求解过程
数值分析中,Range-Kutta法是一种高精度单步算法,是用于求解非线性常微分方程数值解的一类重要隐式或显式迭代法算法,用于数值求解微分方程。由于此算法精度高,采取措施减少了误差,因此,该算法在工程领域中的应用十分广泛。利用该算法需要已知微分方程的一阶导数和初值信息,然后利用计算机仿真技术,节省了求解微分方程的复杂过程。其计算过程如下:
令其初值为
y′=f(x,y),y(x0)=y0,
(7)
由Range-Kutta法:
(8)
其中,
(9)
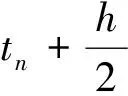
运用数学方法求解式(5)所示的微分方程的解析解,需要联立式(2)~(4),求解该微分方程组难以实现。所以,本文运用Range-Kutta法采用数值解的方法进行求解。
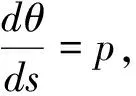
(10)
采用Range-Kutta法求解微分方程组式(10)的一个前提条件是需要已知一个初始位置的挠度y和转角(一阶导数值y′)。但是,对照问题的边界条件,只有s=0,y=0,而s=0的转角值未知。因此,采用迭代法计算求解。其算法流程图如图4所示。
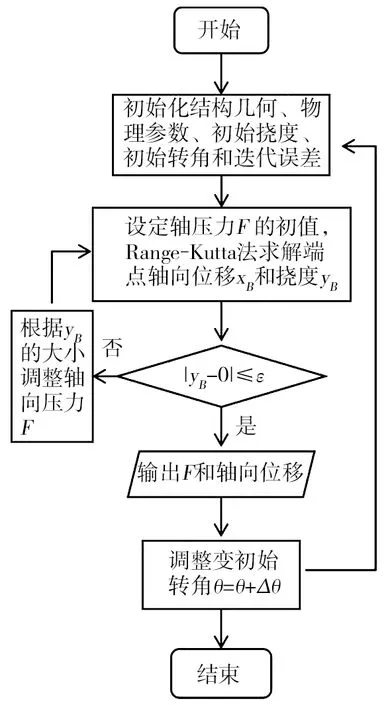
图4 算法流程图
步骤1 初始化结构几何、物理参数,令初始挠度y=0,初始转角θ=0和迭代误差为ε。
步骤2 设定初始轴向压力F,使用Range-Kutta法求解微分方程组式(10),获得挠曲线数值和弹性压杆端点B的轴向位移xB和挠度yB。
步骤3 若|yB-0|≤ε,输出挠曲线方程数值解以及轴向压力F和轴向位移,转步骤4;否则,根据挠度yB与边界值(yB=0)的偏离程度调整轴向压力值。即当yB>0时,适当地增加轴向压力值,当yB<0时,适当减小轴向压力值,然后转步骤2重新计算。
步骤4 改变初始转角θ=θ+Δθ,然后重复步骤1~3的计算过程;循环往复,从而获得弹性压杆轴向压力与位移的关系数据曲线。
3 计算结果与讨论
3.1 初挠度的影响
由图5可知,弹性压杆失稳后轴向压力与位移之间呈非线性关系,并且,初挠度对弹性压杆力与位移关系影响显著。由图6可知,在轴向压力F一定的情况下,弹性压杆的杆端位移量随最大初挠度值e的增大而增大,并且弹性压杆的初始位移量在轴向压力F较小时(F>Fcr)影响较为显著。与初挠度值等于0(e=0 mm)时的情况相比:当最大初挠度e=20 mm且轴向力F=1 644 N时,弹性压杆杆端位移△由1.46 mm增加到207.75 mm;同样,当最大初挠度e=20 mm且轴向力F=4 177N时,弹性压杆杆端位移△由1 107.49 mm增加到1 127.90 mm。
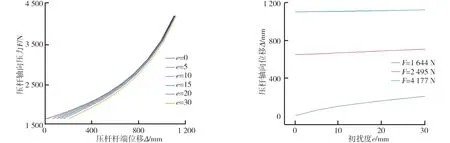
图5 不同初挠度时压杆轴向压力与位移关系曲线图6 轴向压力F相同时初挠度与位移关系曲线
3.2 支承刚度的影响

从图7可以看出,支承刚度对弹性压杆的力与位移关系的影响也十分显著。支承刚度的增加提高了压杆的临界压力;支承刚度越大,弹性压杆的临界压力也就越大。由图8可以看出,轴向位移相同时,支座的支承刚度越大,所需的轴向压力也就越大。与支承刚度K1=K2=0i时的工况相比,当支承刚度为K1=K2=2i,且弹性压杆的杆端位移△=3 mm时,所需的轴向压力由1 643.85 N增加至2 712.03 N,增幅64.98%;同样,当支承刚度为K1=K2=2i,且压杆的杆端位移△=538 mm时,轴向压力由2 275.57 N增加至4 311.07 N,增幅89.45%。

图7 不同支承刚度条件下压杆轴向压力与位移关系曲线图8 轴向压力相同时支承刚度与位移关系曲线
3.3 具有初挠度和弹性支座约束的情形
为了研究弹性压杆在弹性约束和初挠度两种因素共同作用时对弹性压杆力与位移的影响,最大初挠度取值为e=0~20 mm,并令支座约束刚度K1=K2=0i、K1=K2=0.5i、K1=K2=1.0i、K1=K2=1.5i、K1=K2=2i5组组合工况,反复计算得到具有弹性约束和初挠度的弹性压杆轴向压力与位移关系如图9所示。由图9可以看出,不同支承刚度条件下,以压杆最大初挠度和轴向位移为自变量,以弹性压杆轴向压力为因变量的曲面图,该图定量地反应了具有弹性约束和初挠度时弹性压杆的力与位移的关系,其中支承刚度对力与位移关系的影响较为显著。当支承刚度越大且初挠度越小时,弹性压杆临界压力就越大,失稳后产生同样位移需要的轴压力就越大。反之,支承刚度越小且初挠度越大,弹性压杆临界压力就越小,失稳后产生同样位移需要的轴压力也就越小。当弹性压杆的杆端位移达到最大值时,上述5种工况中弹性压杆的轴向压力数据如表1所示。

图9 具有弹性约束和初挠度时压杆轴向压力与位移关系图
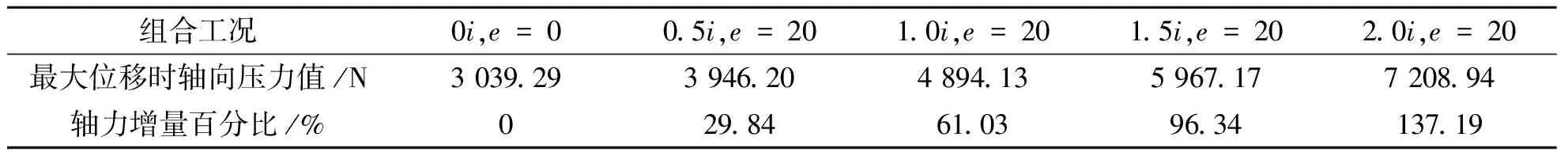
表1 最大位移时各工况轴向压力数据表
4 结论
根据桁架结构中压杆的工作特点,采用大挠度理论建立了求解具有弹性约束和初挠度的弹性压杆轴向压力与位移关系的力学模型和数学模型,并对微分方程采用Range-Kutta法进行求解,确定了具有初挠度和弹性约束的弹性压杆力与位移关系的数值解,为研究桁架结构失稳后的力学行为提供了前提条件。得到的结论如下:
(1)初挠度对弹性压杆轴向压力与位移关系影响显著,初挠度的存在降低了压杆的临界压力;初挠度越大,压杆的临界压力越小;轴向压力一定的情况下,初挠度越大弹性压杆杆端位移也就越大;另外,当轴向压力F较小时(F>Fcr),弹性压杆的初挠度越大其初始位移量就越显著。
(2)支座约束提高了弹性压杆的临界压力,约束刚度越大临界压力也就越大,压杆也就越稳定。与支承刚度K1=K2=0i时相比,当弹性压杆的杆端位移(△=538 mm)一定时,支承刚度为K1=K2=2i时的轴向压力(F=4 311.07 N)比失稳时临界压力(Fcr=1 643.26 N)最大增加了162.23%。
(3)支承刚度和初挠度共同作用时,支承刚度可以在一定程度上抵消初挠度对弹性压杆力与位移关系的影响;初挠度相同时,增加支承刚度可以降低初挠度对弹性压杆力与位移的影响。同样,支承刚度相同时,初挠度越大产生相同位移时需要的轴向压力就越小;当初挠度e=0~20 mm,支承刚度由0~2i时,弹性压杆杆端轴向压力由1 643.26 N增加至7 208.94 N,轴向压力的增量达338.69%。

