基于时域边界元法的散热结构瞬态热传导分析

周枫林，袁小涵，余江鸿，钦 宇，潘先云

（湖南工业大学 机械工程学院，湖南 株洲 412007）

1 研究背景

散热是设备热管理的核心环节，高效的散热机制是高精密设备运行效能的重要保证，不适的工作环境会产生诸多不良影响，例如：1）电子芯片中，随着其计算能力的不断提升，功耗大幅增加，散热性能已经成为制约其进一步提升的瓶颈；2）新能源汽车中，锂电池包作为汽车的主要储能元件，过高的温度不仅会加速电池老化，甚至可能导致电池热失控，引发电芯燃烧爆炸事故；3）航天飞行器中，太阳直射面会产生高温，如果没有配备平衡温差的散热器，温差过大会导致硬件劳损，危及航天安全；4）医疗仪器的精密度和集成度相对较高，设备内部高温容易加速元器件老化，出现性能不稳定或功能失效的故障现象，影响设备的精准度和可靠性。散热器结构中包含许多散热鳍片，其主要工作原理就是增加散热面积，快速散热，有效的热分析有利于改进散热系统，使设备在合适的温度环境中运作。

有限单元法（finite element method，FEM）是一种运用非常广泛的数值分析方法，其采用体积离散技术，将计算域划分为有限个单元，单元与单元之间互不重叠，但是互相连接；然后在每个单元内选择基函数，用每个单元中的基函数来逼近解析解，得出近似解，从而给出整个计算域的解。王瑞等[1]对汽车散热器进行了有限元分析；龙俊华等[2]运用Hyperworks软件对某公司散热器支架进行了仿真分析；王裕林等[3]对某型飞机LED（light-emitting diode）航行灯散热器进行了温度散热分析；王金龙等[4]通 过ANSYS软 件 对CPU（central processing unit）水冷散热器进行了数值模拟，并根据分析结果对结构进行了优化；刘贝等[5]利用有限元软件对翅片式相变散热器进行了仿真分析，并根据仿真结果对散热器结构进行了优化设计，改善了其散热性能。

上述研究中使用的软件，其底层算法框架都是基于有限单元法[6-8]，虽然有限单元法已发展成熟，是一种可靠的数值分析方法，但有限单元法需要对整个模型进行离散，计算数据庞大，计算耗时长。随着传热学的发展，数值计算方法有了极大的进步，越来越多的方法被用于传热学问题，常用的有边界单元法（boundary element method，BEM ）[9-11]、有限差分法[12-13]、无网格法[14]，其中，边界单元法只在研究区域的边界上剖分单元，涉及的计算域较小，网格划分较少，除了能处理有限单元法所适应的大部分问题外，还能处理有限单元法不易解决的无限域问题。如徐闯等[15]运用边界元法对功能梯度材料进行了热传导分析；肖雄等[16]对正交各向异性功能梯度材料的瞬态热传导问题进行了边界元分析，证明了边界元法的可靠性；Yu H.P.等[17]运用等几何边界元法对电子封装结构进行了热分析。但对于边界元法在三维瞬态热传导问题上的工程运用研究尚不多见，还有待进一步研究。故本研究将运用双互易边界元法和精细积分方法耦合来分析散热结构。

本文是在热力学理论基础上，对散热器结构进行热传导分析，推导了不含内部热源的各项同性介质瞬态常系数热传导问题的边界积分方程，将该积分方程运用到散热器的计算边界上，然后使用精细积分法求解边界离散后得到的常微分方程组。经过与有限元计算结果的对比，验证了边界元方法的准确性，并具有计算量小的优点。

2 双互易精细积分边界单元法

散热器的热传导分析中，散热器的材料大部分为铝，因而本文的工况条件设定如下：热传导系数不随温度变化，工作过程中不含内部热源，材料为各向同性介质。于是，在其三维瞬态热传导问题中，其控制方程可表示如下：

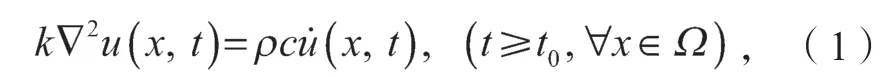
边界条件设定如下：

式中：q为热通量；为边界上的已知热通量；Su表示狄利克雷型边界；Sq表示诺依曼型边界；Su+Sq=Γ，为计算域Ω的所有边界；n为边界的单位外法线方向向量。

初始条件如下：

对于不含内部热源的三维瞬态常系数热传导问题的控制方程，运用加权余量法推导其边界积分方程。引入权函数，则式（1）的加权余量式为

根据高斯散度定理和三维位势问题的基本解，运用分部积分法将式（4）中的左边域积分转化为如下内部点积分方程：

当源点位于边界时，需要对边界进行拓扑，对于三维情况，可以得到如下边界-域积分方程：

式中：

其中θ为边界点处的切面所围成的立体角。

选择如下RBF：

式中：r为RBF插值点到源点的距离；s为形状参数；i为总插值点数。

令

式中F为径向基函数矩阵。

将式（8）代入式（6），得

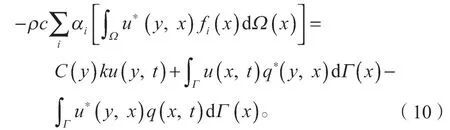
令

将式（11）代入式（10）中，再次运用高斯散度定理和三维位势问题的基本解，可以得到如下边界积分方程：

式中：

在边界积分方程式（12）中，不再涉及域积分，其中温度对时间的一阶导数项已被等效边界积分所代替。与有限元法不同的是，因为未知量u和q都是在边界上取值，故只需对边界进行离散，可得：

式中：j为边界单元个数；m为单元中的节点数，本文采用8节点二次面单元，m=8。

将源点遍及所有的边界节点，可以得到如下矩阵形式：

式中：H和G为影响系数矩阵；矩阵上方的字母为矩阵维数，其中b为边界节点个数，d为域内节点个数。

将式（9）代入式（15），可得：

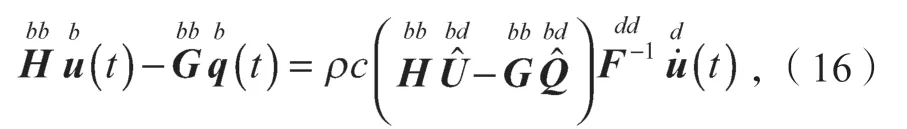
改写为如下矩阵形式：

考虑如下边界条件：

式中，C1和C2为对角矩阵，对角元素的取值根据边界条件的类型确定如下：

将式（18）引入式（17），可得：

则边界节点上的量可表示为

式中：

此时考虑内部点，将式（16）改写为如下形式：

将式（21）代入式（22），可得内部节点上的量：

式中：

精细积分法可用于求解该一阶常系数微分方程组，式（23）的通解为

式中：Δt=tk-tk-1；tk=kΔt。

矩阵指数函数

可被细分为

式中，M为细分参数。

式中：P为截断参数；Er为式（28）中I的后P项。则式（27）可改写为

再次细分，通过循环语句重复计算和重新赋值，最终可得

3 山型散热器结构热传导分析

本文分析用山型散热器结构的简化模型及尺寸（单位为m）如图1所示。因为散热器材料主要为6063铝，其热传导系数不随温度而变化，故假定其热导率、热容和密度分别为1 W/(m·℃)，1 J/(kg·℃)和1 kg/m3。

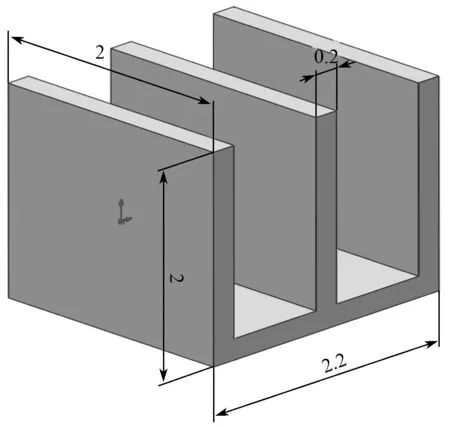
图1 山型散热器结构及其尺寸示意图Fig.1 Schematic diagram of structure and size of the gable radiator

3.1 有解析解工况下的BEM

对于前文所提到的双互易精细积分法（precise integration-dual reciprocity boundary element method，PI-DRBEM），本节将给出一个算例，通过将PIDRBEM的结果与解析解进行对比，验证其准确性和有效性。

定义如下相对误差：

对于细分参数M和截断参数P，本文分别取10和6。

模型的边界划分如图2所示。

图2 模型边界划分示意图Fig.2 Boundary division diagram of the model

本算例中，Γ1和Γ2为诺依曼型边界，其条件假定如下：

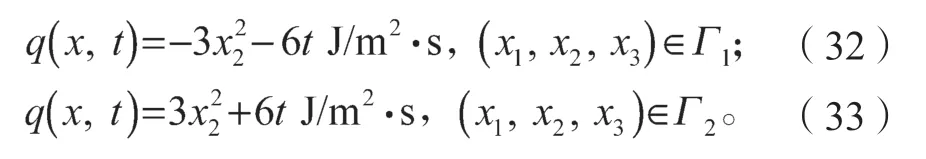
其余边界为狄利克雷型边界，其条件假定为

本算例不含热源，初始条件给定为

此时根据控制方程式（1）可得解析解为

RBF插值点分布如图3所示。

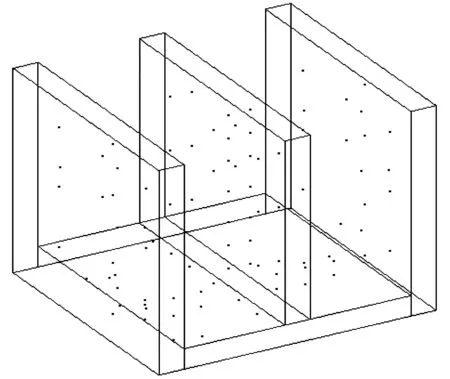
图3 RBF插值点分布示意图Fig.3 Distribution diagram of RBF interpolation points

整个计算域被划分为180个矩形单元，总共800个边界节点，92个RBF插值点。考虑不同时间步长下域内温度与解析解的相对误差情况，所得结果如图4所示。

图4 温度随时间变化的相对误差曲线Fig.4 Relative error curves of temperature with time

图4中共给出了5种不同时间步长下，温度随时间变化的相对误差曲线，由图可知，当时间步长为0.1 s时，其相对误差曲线位于最下方，表明同一时刻的相对误差值最小，此时，即使是在接近初始时刻的第5 s，其相对误差值也很小，具有较高的精确度。并且随着时间的推进，相对误差值越来越小，数值解也越趋近于解析解，说明BEM在分析山型散热结构的热传导问题时是有效可靠的。表1给出了点A(0.600 0, 0.916 7, 0.625 0)在不同时间步长下的温度情况，并给出其对应的温度解析解。

表1 A点在不同时间步长下的温度情况Table 1 Temperature of point A at different time steps ℃

由表1可以得出，在所给出的5种不同时间步长下，其所求温度值与解析解的最大差值为2.07 ℃，出现在时间步长为2.5 s时的第50 s时刻；最小差值为0.959 ℃，出现在时间步长为0.1 s时的第5 s时刻。可见，所有时间步长下的数值计算结果和解析解几乎吻合，进一步验证了BEF在山型散热器模型分析中的精确性。

3.2 无解析解工况下的BEM与FEM对比

通常情况下很难获得系统的解析解，故本小节将在无解析解的工况下，将FEM分析软件（Workbench）的结果与BEM结果进行对比分析。假定散热器底面的温度变化情况为与时间相关的二次函数，以近似于实际工况下的温度变化情况。

底部边界条件为狄利克雷型边界，其条件如下：

无热源项时，初始条件给定为常温：

有限元分析模型的网格划分如图5所示。

图5 山型散热结构的有限元网格划分示意图Fig.5 Schematic diagram of finite element mesh division of mountain heat dissipation structure

图5所示结构中，单元尺寸定义为0.05 m，共划分为24 320个线性六面体网格，共有118 217个节点；时间步长取1 s。

对于边界元法，时间步长同样取1 s，然后在上一个算例的基础上，加密边界网格划分，将整个计算域划分为500个矩形单元，节点数为1 920个，RBF插值点数为164个。可以明显看出，不论在单元个数还是节点个数上，边界元法都远远少于有限元法，故其计算量相对低很多。

对于这两种方法，考虑同一点B(0.75, 0.91, 0.52)，该点温度在两种数值方法的计算下，随时间的变化情况如图6所示。

图6 B点PI-DRBEM和FEM的计算温度对比曲线Fig.6 Calculated temperature comparison curve of PIDRBEM and FEM at point B

由图6可知，在开始时刻附近，PI-DRBEM的温度计算结果和FEM的温度计算结果间有一点出入，但随着时间推移，两结果趋于吻合，对比表明，边界元法和有限元法同样具有很高的可靠性和精确性，并且具有计算量更小的优点。

4 结语

对于山型散热器结构的瞬态热传导问题，本文运用了双互易方法与精细积分方法耦合进行计算求解，并在理想工况下与解析解进行对比，在实际工况下与FEM的分析结果进行对比，两种工况下的对比结果都验证了PI-DRBEM的准确性和有效性。在与FEM进行分析对比时，可以很清楚地得知边界元法具有计算量小、求解所需内存小、计算效率高的特点，同时还能保证计算结果的精确性。

本研究论证的边界元法，对于散热器结构分析来说是一种有效的方法，对于所有机械设备的散热分析有很大的帮助，有利于改善散热器结构布局，提高设备运作稳定性。