焊接工艺对波形钢腹板焊接细节残余应力的影响

刘 扬，马 威，张海萍，邓 扬，李 立

（1.湖南工业大学 土木工程学院，湖南 株洲 412007；2.北京建筑大学 土木与交通工程学院，北京 100044）

0 引言

由于波形钢腹板-翼缘板焊接构件在焊接过程中受热不均匀，导致焊缝细节存在较为复杂的焊接残余应力场[1]。焊接残余应力的存在会影响焊接构件的疲劳强度，以及疲劳裂纹扩展路径[2-4]。为减小焊件的残余应力，许多研究者通过改变焊接工艺参数分析了影响焊接残余应力的因素[3-9]，但是关于波形钢腹板-翼缘板焊件残余应力影响因素方面的研究鲜有报道，因此，有必要提出一种合理的波形钢腹板-翼缘板焊件焊接工艺。

近年来，国内外学者们主要研究了热源输入和焊接顺序等因素对焊接构件残余应力的影响。例如李磊等[5]基于热弹塑性有限元分析方法，建立了典型船舶构件焊件，通过研究，得出焊接等效残余应力与焊接速度呈负相关，但是焊接速度过快会影响焊接质量的结论；A.Khoshroyan等[6]采用Ansys对铝合金T型焊件进行了研究，发现焊接速度的提高能够增加焊缝的纵向拉应力；此外，较高的电流输入也会增加其残余应力；Yi J.等[7]通过对4种不同焊接顺序的铝合金焊件残余应力进行对比，指出合理的焊接顺序能有效降低焊接残余应力；兰亮云等[8]也认为焊接顺序对残余应力存在一定的影响，并且指出，对于双面焊焊件，先焊完一侧再焊接第二侧能减小焊件的整体残余应力水平；徐捷等[9]指出，顶板-U肋双面焊模型焊缝附近的残余应力较单面焊模型的低，其还认为采用先后焊接的方案能够降低先焊接焊缝一侧的残余应力，这与兰亮云等得到的结果相似。之所以出现这样的结果，文献[10]中认为，第二道焊的加载过程对焊件起到了回火作用，这进一步论证了文献[11]中指出的多道焊焊件中最后一道焊是影响焊件残余应力分布的关键。

本文拟采用有限元分析软件ABAQUS建立波形钢腹板-翼缘板单面焊焊件和双面焊焊件模型，探讨焊接顺序对单面焊焊件残余应力的影响，分析焊件分别采用单面焊和双面焊工艺时残余应力的分布情况，以期为提出一种合理的波形钢腹板-翼缘板焊件焊接方法提供理论参考依据。

1 波形钢腹板焊接残余应力数值计算

本研究以头道河大桥为工程背景。头道河大桥上部采用了波形钢腹板组合结构，波形钢腹板钢材为Q355NHC，波长为1.6 m，波高为0.22 m，钢板厚度为14～24 mm，水平子板宽度为43 cm，斜板宽度为37 cm，平板与斜板间的夹角为30°，且连接处采用内径R为15t（t为波形钢腹板的厚度）的圆弧段过渡，典型波形钢腹板构造如图1所示。

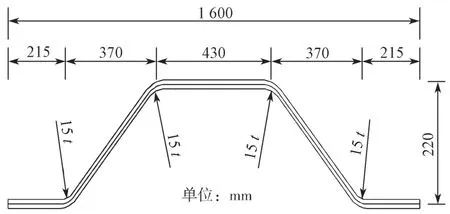
图1 波形钢腹板构造示意图Fig.1 Schematic diagram of corrugated steel web construction

1.1 模型尺寸

考虑到波形钢腹板-翼缘板构件的周期性，只建立一个周期的模型，其连接构造与尺寸如图2所示。波形钢腹板厚度为20 mm，波折转角半径r为150 mm，波折角度θ为30°，波形钢腹板高度h为100 mm，翼缘板宽度b为500 mm，翼缘板长度l为811.051 mm，由于实桥为变截面，分别建立钢翼缘板厚度为14, 17, 20 mm的数值模型进行对比研究。

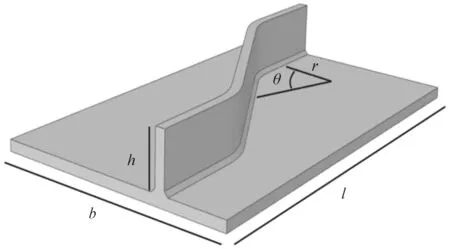
图2 波形钢腹板-翼缘板焊件有限元模型Fig.2 A finite element model of corrugated steel web-flange weldment

1.2 材料热物理性能

假设数值模型的母材和焊条热物理、力学性能相同，均采用Q345钢材，材料参数随温度变化曲线如图3所示[12-14]。

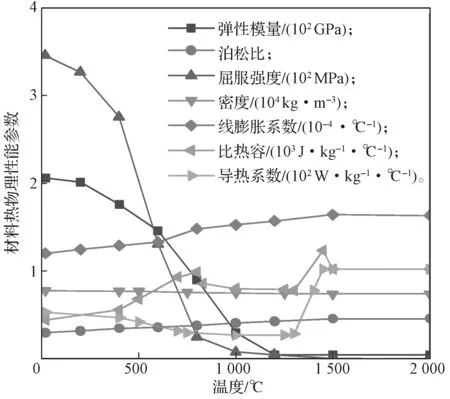
图3 Q345钢材热物理材料参数Fig.3 Thermophysical material parameters of Q345 steel

本研究数值计算过程中，常数Stefan-Boltzmann取5.67×10-8W·(m2·℃4)-1，绝对零度为-273.15 ℃。对流换热系数受诸多外界环境条件的影响，自然条件下，空气的自然对流系数为5～25 W/（m2·℃），本研究中取20 W/（m2·℃）。辐射换热系数取定值0.8，环境温度取20℃[15]。

1.3 网格划分

为确保计算精度，本研究建立了4种不同网格尺寸的平板焊件模型，网格尺寸依次为1.0, 2.5, 5.0,10.0 mm，仿真试验得到各模型的纵向残余应力随距离的变化结果，如图4所示。

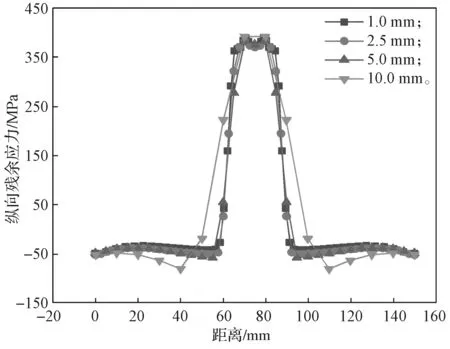
图4 不同网格尺寸焊件模型的纵向残余应力随距离的变化曲线Fig.4 Longitudinal residual stress curves of weld models with different mesh sizes varying with distance

分析图4可以得知，当平板焊件模型的网格尺寸为10.0 mm时，焊缝附近的应力分布偏差较大，而当网格尺寸减至5.0, 2.5, 1.0 mm时，其应力分布完全一致，且应力峰值位置及数值吻合度较高。综上所述，为兼顾计算效率和计算精度，焊缝区域采用较细密网格（网格尺寸约为2.5 mm），远离焊缝区域采用较稀疏网格（网格尺寸约为10 mm），其他区域则划分出至少两个过渡区，实现网格尺寸从横向和纵向上的过渡。图5为30°波折角度焊件的网格划分模型。为高效率模拟焊接过程中焊缝的不断填充，首先统计焊件焊缝单元编号，然后采用Python实现“生死单元技术”，最终计算出焊件的焊接残余应力。

图5 30°波折角度焊件的网格划分模型Fig.5 Meshing model of weldment with a wave angle of 30°

1.4 焊接热源

焊接热源参数的选取会直接影响整个焊件的焊接残余应力与残余变形量，因此焊接热源的确定是整个仿真过程中一个非常重要的步骤。ABAQUS中焊接移动热源的实现，主要采用Fortran语言编制的DFLUX子程序加载方式，子程序的编写主要涉及如下两个方面的问题。

1）焊接移动热源模型的选取。本文选用双椭球热源[16]，热源分布模型如图6所示。

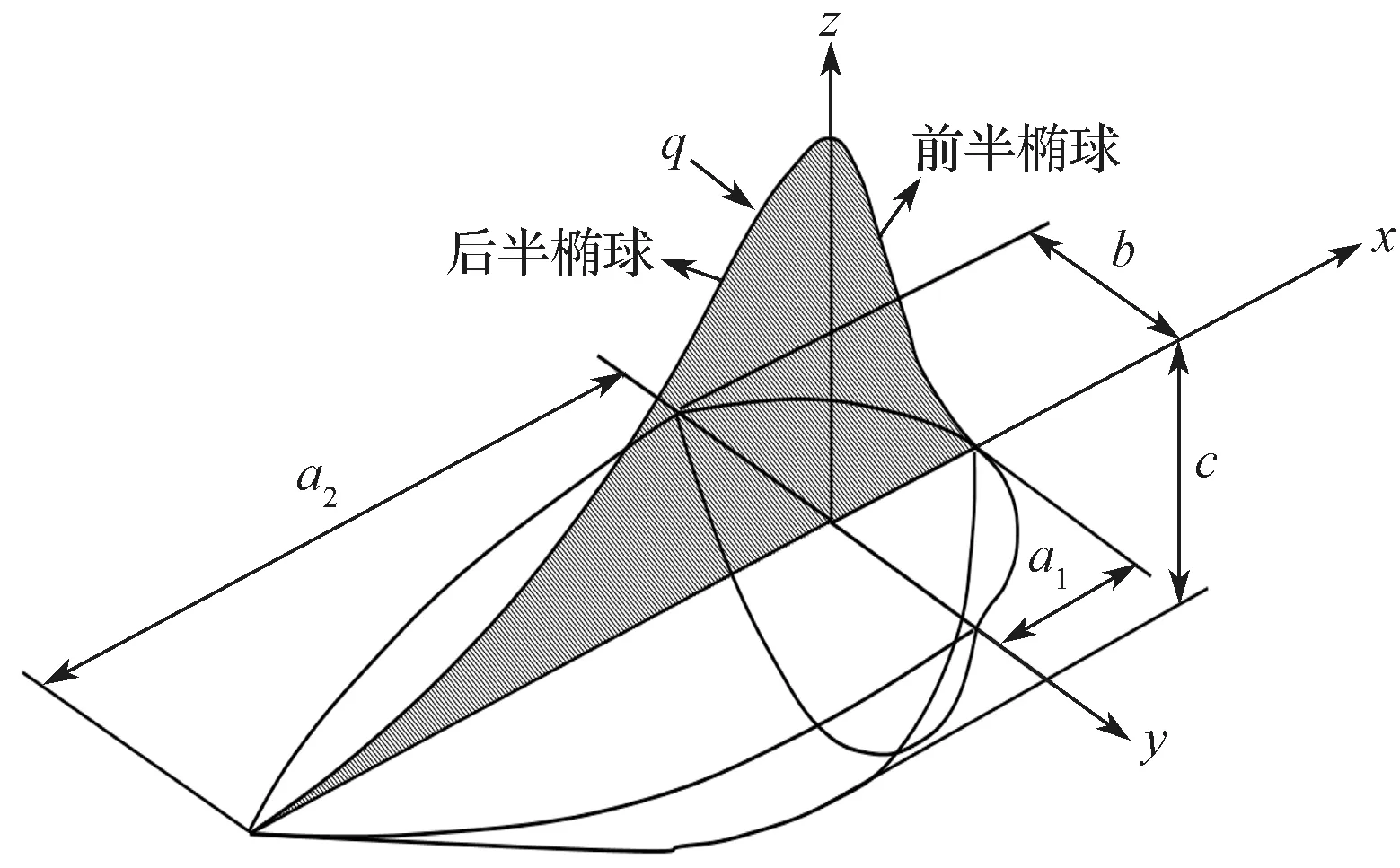
图6 双椭球热源分布模型Fig.6 Double ellipsoid heat source distribution model

椭球前半部分的热流密度函数分布如下：

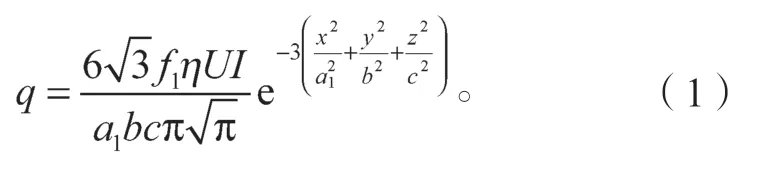
椭球后半部分的热流密度函数分布如下：

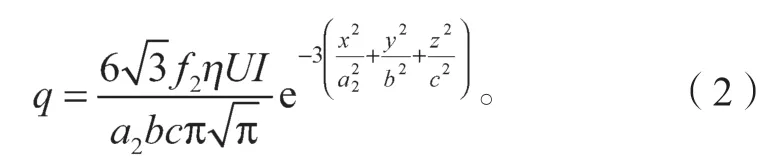
式（1）（2）中：U、I分别为焊接电压和电流；

η为热源效率；

f1、f2为能量分级函数；

a1、a2、b、c均为椭球形状参数。

2）双椭球热源模型参数的选取。为使焊接过程中焊缝完全熔透，首先建立一组初始的热源模型参数，然后根据计算过程中得到的熔池宽度、熔池深度对热源参数进行修正，最终得到完全熔透焊缝的热源模型，熔池模型如图7所示。

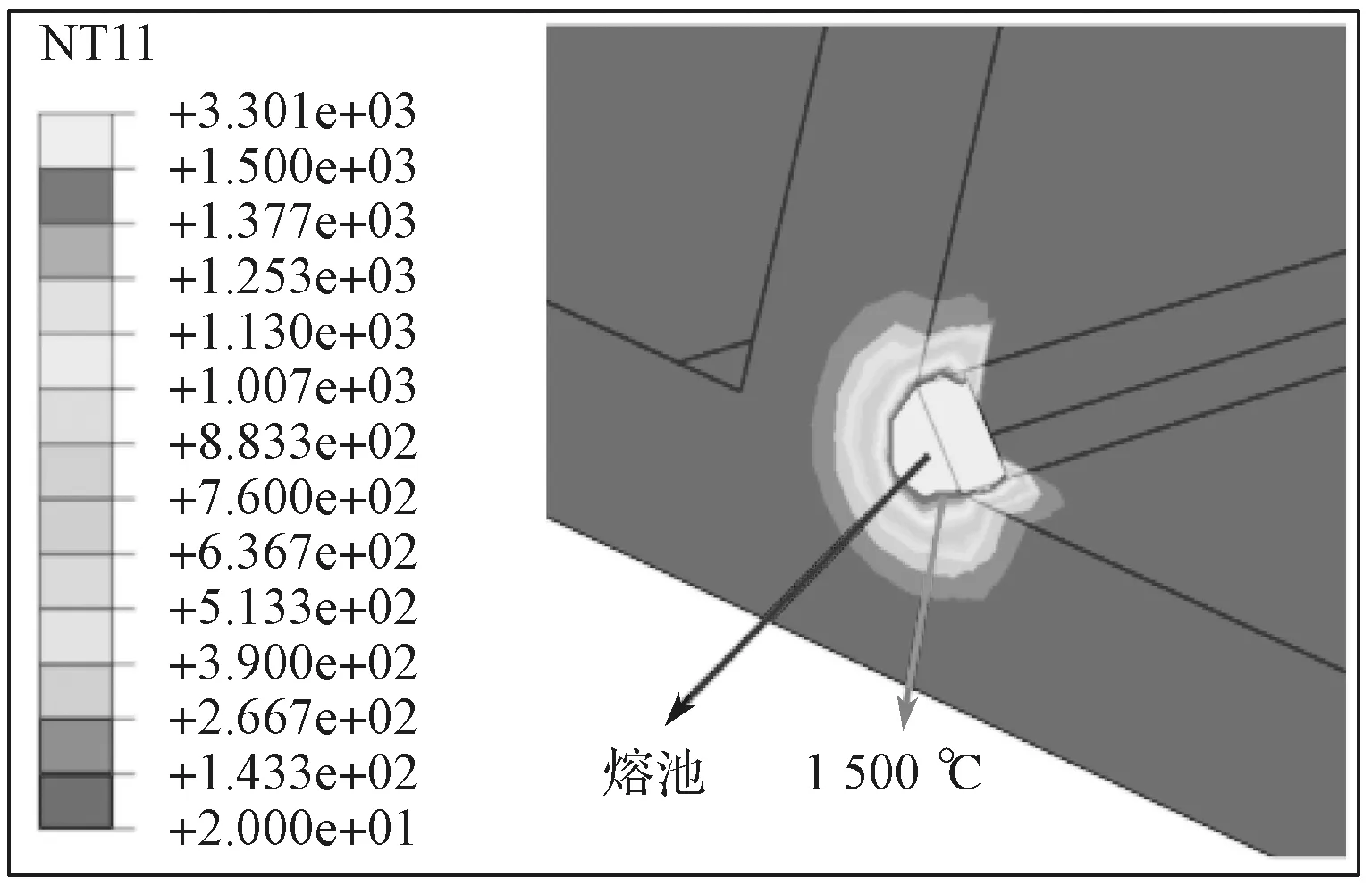
图7 焊缝的熔池模型Fig.7 Welded pool model

由图7可知，熔池温度高于1 500 ℃，这表明热源参数满足要求。

1.5 位移边界条件

温度场的计算仅是一个热传递过程，无需设置位移边界条件，而应力场的计算则需要考虑刚体位移对应力场结果的影响，需要给焊件一个位移边界条件，同时不能严重阻碍关注细节处焊接残余应力的发展过程。最终在远离焊缝区域的钢腹板上施加完全固结边界条件，边界条件设置如图8所示。

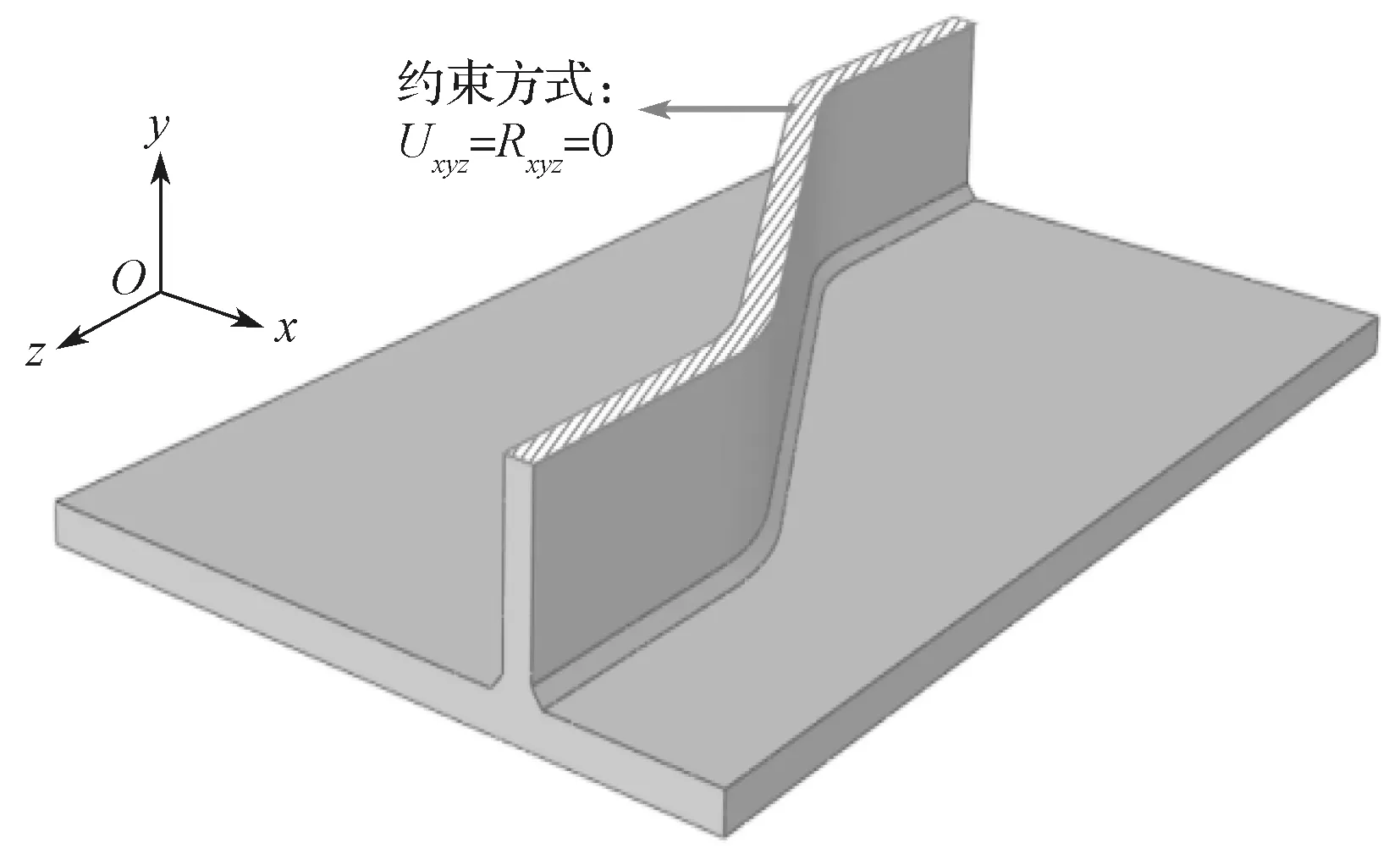
图8 边界条件设置图Fig.8 Boundary condition setting diagram

1.6 焊接工况

为研究不同焊接工艺对焊接残余应力的影响，建立了采用单面焊焊接工艺和双面焊焊接工艺的数值计算模型，具体的焊接工况如图9所示。如图所示，采用单面焊焊接工艺的计算模型，选用工况一、工况二两种相反路径的加载方式，其中工况一中包含3种（14, 17, 20 mm）翼缘板厚度模型计算，用来探讨截面尺寸变化的影响；采用双面焊焊接工艺的计算模型选用工况三的加载方式，并且将焊件模型分为前部和后部两个区域。

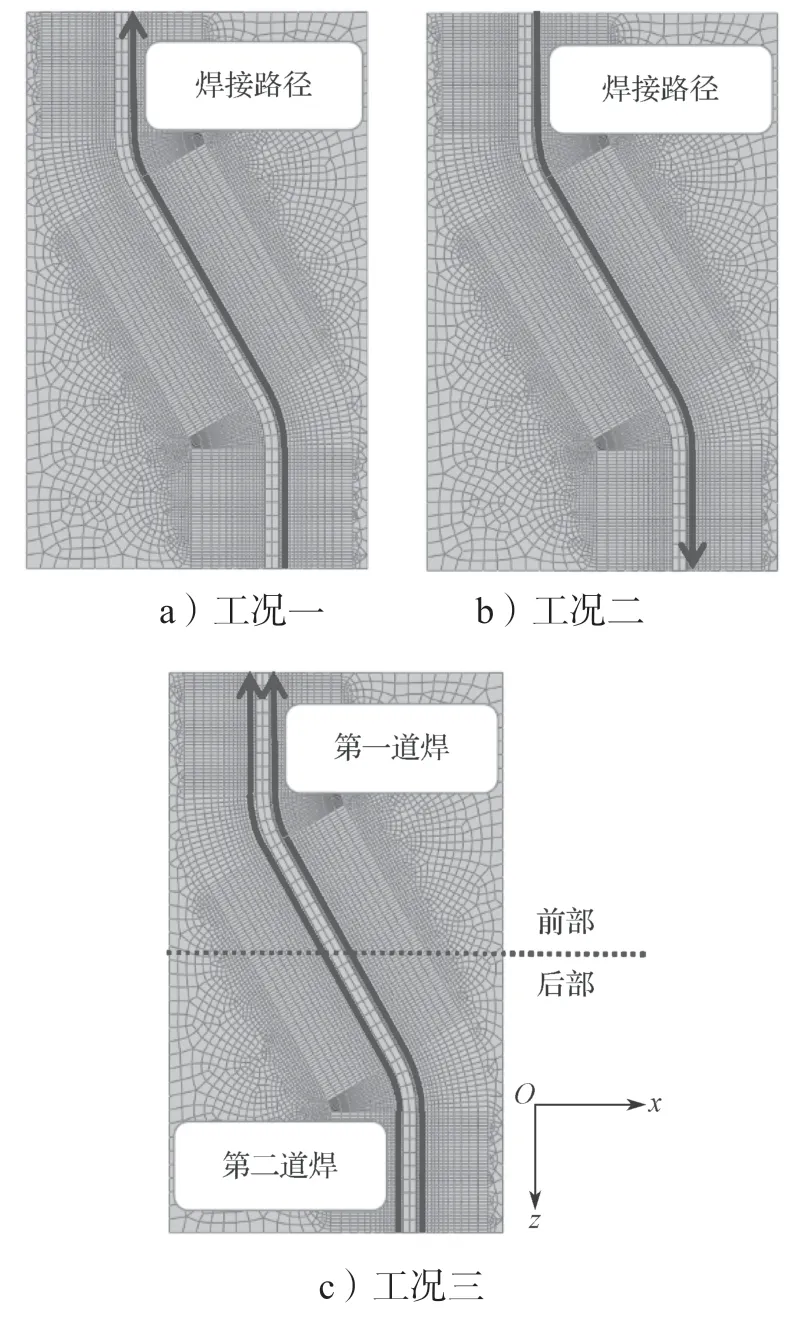
图9 焊接工况示意图Fig.9 Schematic diagram of welding conditions

2 焊接温度场结果与分析

2.1 温度场云图

本文计算两种不同焊接工艺的焊件模型，其中双面焊焊件在第一道焊缝完成后直接开始焊接第二道焊缝，两种焊件焊接完成之后均冷却3 000 s。限于篇幅，本文仅给出双面焊焊件焊接-冷却阶段的温度云图，如图10所示，其焊接时程为346 s，冷却时程为3 000 s。

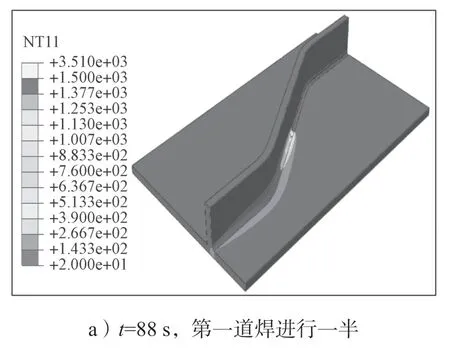
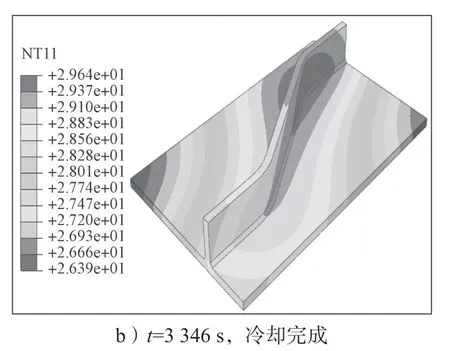
图10 焊接-冷却阶段温度场云图Fig.10 Temperature field cloud diagram in welding and cooling stages

从图10中可以看出，波折角度为30°的双面焊焊件上温度场的分布取决于移动热源的位置，热源到达区域的温度迅速上升至超过钢材的熔点温度（约为1 500 ℃），随着热源逐渐远离，高温区域的温度逐渐下降，当焊件焊接完成之后，整个焊件的温度逐渐降低，最终在3 000 s后降低至26～29 ℃，可以认为焊件温度逐渐冷却至室温。

2.2 温度循环曲线

选取第一道焊缝路径为测点路径，测点路径上随着焊接方向，分别为测点1～5。测点包括波形钢腹板直边中心位置、转角区域中心位置及斜直边中心位置，具体分布见图11，经过仿真试验，得到了各测点温度随时间变化的关系曲线，如图12 所示。

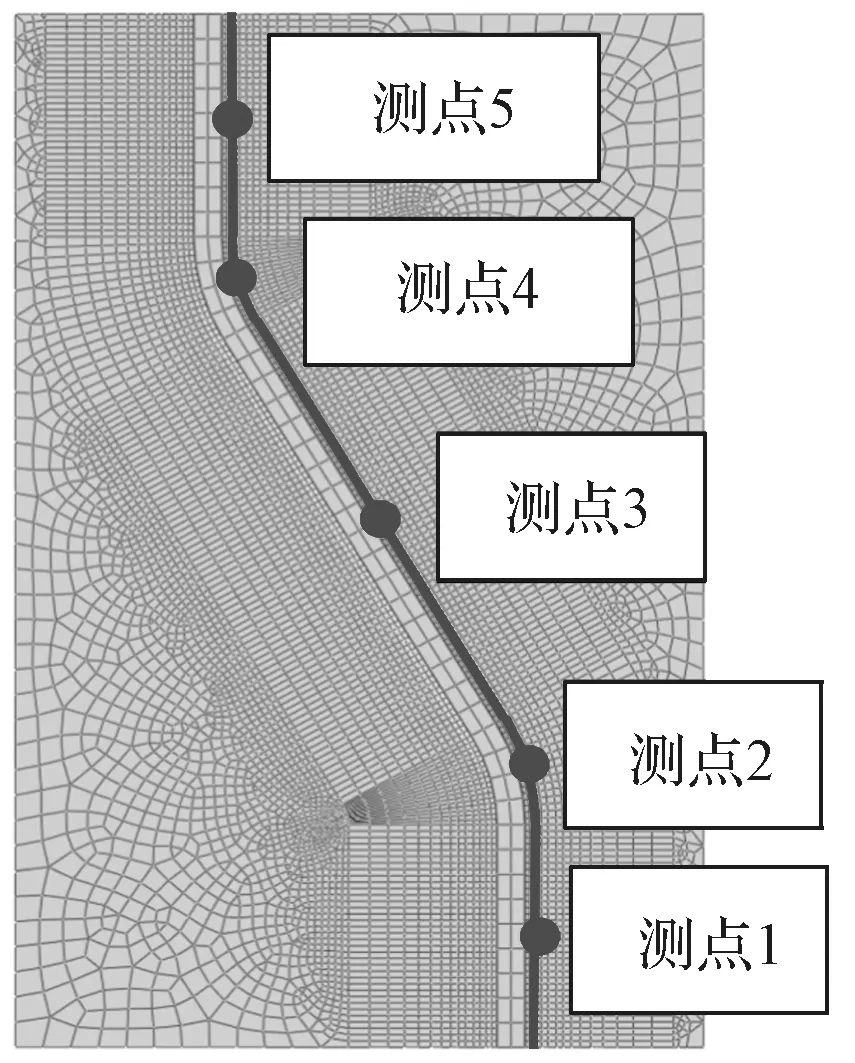
图11 测点分布图Fig.11 Distribution of the measuring points

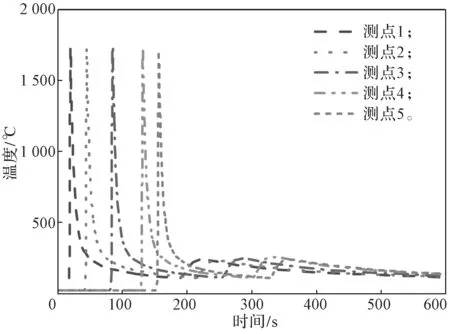
图12 不同测点温度随时间变化曲线Fig.12 Temperature curves with time at different measuring points

由图12可知，各测点温度随着热源的移动而变化，当热源移动到测点附近时，测点温度急剧上升，约至1 700 ℃；随着热源的远离，温度逐渐降低，热源在进行第二道焊时再一次接近测点，温度再一次呈现上升趋势。对比图12中各曲线，可以发现各测点温度均有两个峰值点，且不同测点的峰值点温度基本一致，这表明焊件的整个焊缝区域是一个准稳态温度场，各焊缝的焊接效果较为理想。

3 焊接残余应力场结果与分析

3.1 应力场云图

从前文的温度场分析，可知焊接过程较为理想，将得到的温度场结果作为初始条件（预定义场）代入应力场进行计算，冷却完成后得到的3种加载工况应力场云图如图13所示。

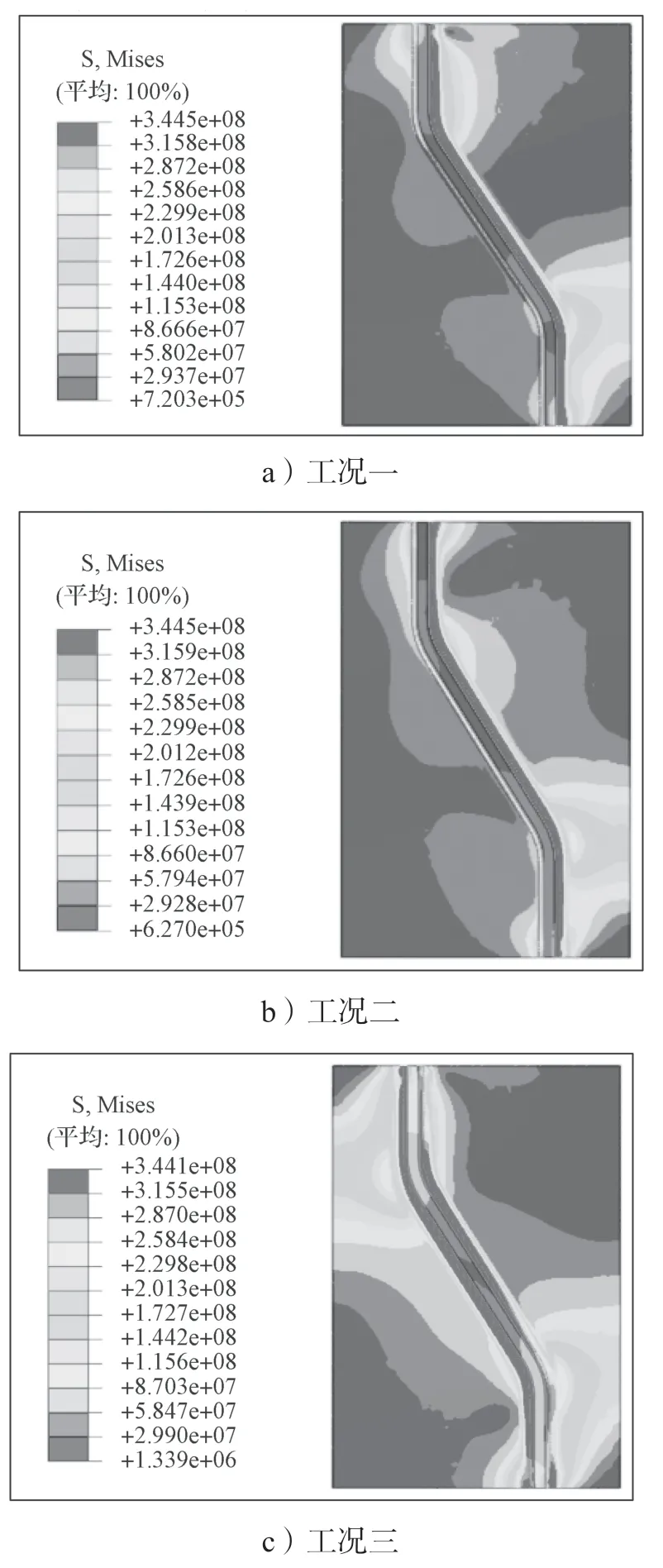
图13 冷却完成后得到的不同工况应力场云图Fig.13 Cloud images of stress field obtained under different working conditions after cooling

从图13中可看出，3种模型冷却完成时的最大应力均存在于焊缝附近，翼缘板上均呈现S分布，随着远离焊缝，应力逐渐变小，最大Von Mises应力约为344 MPa，接近Q345钢材的屈服强度。对比图13中各工况云图可看出，采用双面焊接工艺的焊件在直边和后部折角区域焊缝的等效残余应力较单面焊焊件明显降低。

3.2 有限元模型验证

提取波形钢腹板-翼缘板双面焊件在斜直边上的焊接残余应力，与文献[1]中的试验结果进行对比验证，结果如图14所示。

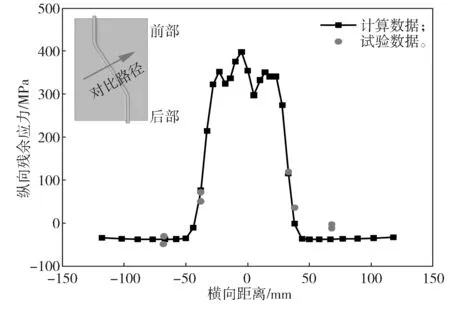
图14 试验数据与计算数据对比图Fig.14 Comparison diagram of test and calculated data

由图14可知，本研究有限元数值模拟所得残余应力曲线与文献[1]中的试验实测数据的吻合度较高。由此可见，基于热-力顺序耦合有限元模拟方法计算精度满足要求。

3.3 不同加载工况下的应力结果与分析

基于疲劳裂纹易萌生于波折角焊缝焊趾处，且沿横向发展这一现象[17-18]，本研究主要研究各焊接工况下焊件折角区域的焊接纵向残余应力分布及其影响因素。首先，定义垂直于焊接路径方向为横向，平行于焊接路径方向为纵向，然后在焊件翼缘板上选择用于提取残余应力的横向路径Ai、Bi、Ci，提取路径主要分布于折角焊缝区域，如图15所示。

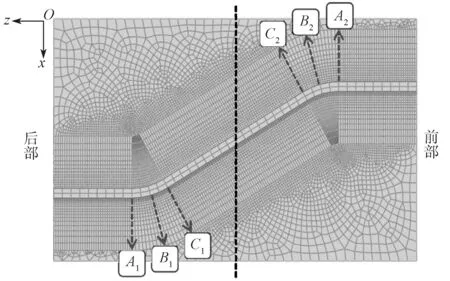
图15 焊接残余应力的提取路径Fig.15 Extraction path of welding residual stress

仿真所得3种工况加载情况下的折角区域纵向残余应力分布如图16所示。

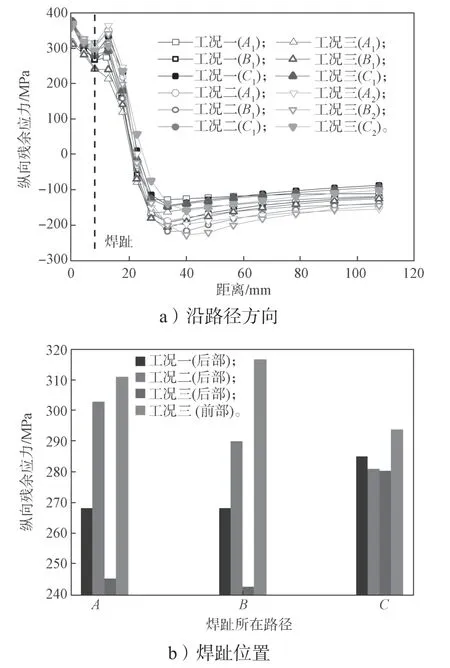
图16 不同工况下折角区域的残余应力分布图Fig.16 Residual stress distribution in the corner area under different working conditions

从图16中可知，各工况加载情况下的纵向残余应力峰值点均位于焊缝附近，随着远离焊缝，残余应力逐渐降低。对比图中工况一和工况二可知，单面焊采用不同焊接路径对焊根处残余应力的影响较小，而对焊趾处残余应力的影响较大。工况二加载情况下，路径A1、B1焊趾处的残余应力比工况一分别高38,23 MPa。对比图中工况一和工况三，可发现双面焊焊件在路径A1、B1、C1焊根处的残余应力比单面焊焊件分别低54, 51, 54 MPa，双面焊焊件在路径A1、B1、C1焊趾处的残余应力比单面焊焊件的分别低23,27, 28 MPa，可得出，采用工况三加载的双面焊焊件能较大程度地降低后部折角区域焊缝的残余应力。这与前面得到的应力云图分析结果一致，其原因可能是第二道焊缝的加热过程起到了回火作用[9]，使得焊件的残余应力峰值位置重新分布。

从图9中可看出，工况二的焊接路径与工况三中第二道焊的路径一致，为研究第一道焊对第二道焊的影响，认为工况二中的数据提取路径A1、B1、C1等同于工况三中的A2、B2、C2，工况二和工况三加载情况下的前部折角区域焊接残余应力分布如图16所示。对比图16中工况二和工况三，双面焊焊件在路径A2、B2、C2焊根处的残余应力与单面焊焊件无较大差异，双面焊焊件在路径A2、B2、C2焊趾处的残余应力比单面焊焊件分别高8, 31, 10 MPa，可得知采用工况三加载的双面焊焊件前部折角区域焊缝残余应力较单面焊焊件高，尤其在转角中心焊缝焊趾处。

3.4 不同尺寸模型应力结果与分析

考虑到实桥为变截面尺寸，计算出工况一加载情况下翼缘板厚度分别为14, 17, 20 mm的焊件残余应力结果分布，所得关键细节的纵向残余应力结果如图17所示。

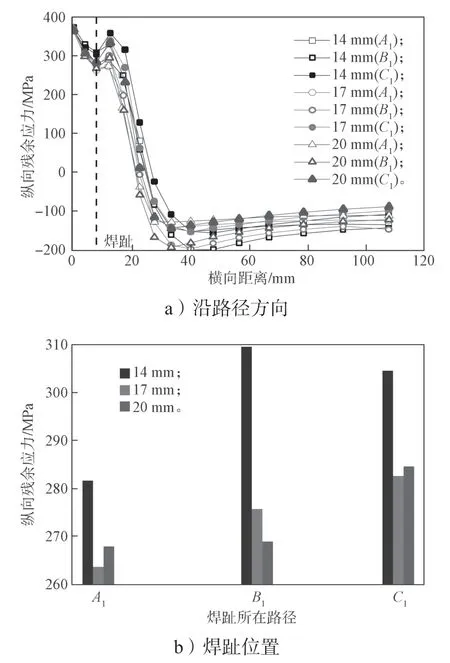
图17 不同尺寸模型折角区域的残余应力分布图Fig.17 Residual stress distribution in the corner area of different size models

从图17中可看出，不同翼缘板厚度模型应力结果的纵向残余应力峰值点均位于焊缝附近，并且随着远离焊缝而逐渐降低，随着板厚的增加，整个折角区域焊趾的纵向残余应力大致呈下降趋势，尤其在翼缘板厚度从14 mm增至17 mm时较为明显，路径A1、B1、C1焊趾处的残余应力分别减小18, 34, 26 MPa；但当厚度从17 mm增至20 mm时，仅路径B1焊趾处（折角中心位置）的残余应力减小了7 MPa，而路径A1、C1焊趾处残余应力分别增加了4, 2 MPa，整体变化幅值较小，可认为无较大变化。分析其原因，可能为数值计算过程中，随着翼缘板厚度增加，热流量输入恒定，相同体积所受的热流影响变小，使得纵向残余应力减小。

4 结论

本文结合“生死单元技术”和“热-力顺序耦合计算方式”对3种不同焊接工况的波形钢腹板-翼缘板焊接构件进行数值计算，对比了单面焊件在不同焊接顺序下的纵向残余应力分布，分析了单面焊件和双面焊件在折角区域焊缝的纵向残余应力分布，考虑了变截面对单面焊件关键细节纵向残余应力的影响，得出如下结论：

1）焊接等效残余应力在焊缝附近达最大值，为344 MPa，接近Q345钢材的屈服应力，故在进行波形钢腹板梁桥焊接细节的疲劳分析时，应考虑焊接残余应力的影响。

2）不同焊接顺序能影响单面焊焊件折角焊缝焊趾的残余应力，选择合理的焊接顺序能降低20～40 MPa的纵向残余应力。

3）采用工况三加载方式的双面焊焊件，能较大程度降低后部折角区域焊根、焊趾处的纵向残余应力，但是会提高前部折角区域焊趾处的纵向残余应力。因此，为减小折角焊缝区域的焊接纵向残余应力，建议采用先焊折角圆弧外侧，再焊圆弧内侧的双面焊焊接工艺。

4）在波形钢腹板厚度恒定时，翼缘板厚度的变化能影响关注细节的纵向残余应力分布，折角区域焊趾的纵向残余应力与翼缘板厚度大致呈负相关，且在折角中心位置处较为明显。