基于高温质子交换膜燃料电池和全钒液流电池的离网能源系统的配置优化

黄雅琨，刘进一，张筱松

（海南大学机电工程学院，海南省 海口市 570228）

0 引言

随着我国能源结构的调整，风电、光伏、氢能等清洁能源逐渐成为我国能源供给侧改革的发力点。燃料电池作为氢能的主要应用载体之一，目前已经广泛应用于精密仪器、电子通信、交通工具以及区域性电站等场景中，显示了其广泛的市场适用性。当燃料电池作为独立的电力供应系统时，最大的问题是其不能很好地跟随负载功率需求的变化，若将其和储能技术结合，构成混合能源系统，可以很好地弥补燃料电池在动态供能上的缺陷，挖掘节能降耗的巨大潜力。

目前，有很多学者针对混合能源系统在不同场景下的实际应用展开了研究分析。如何丽美等[1]提出了基于质子交换膜燃料电池(proton exchange membrane fuel cell，PEMFC)/膨 胀 机 的冷热电联供系统，发电效率、热效率以及总效率分别可达到56.2%、35.2%和91.4%，实现了对可再生能源的高效利用。孔令国等[2]针对离网电氢耦合系统提出了基于模型预测控制的功率调控方法，对储能系统的稳定性及氢储能系统的利用率有较大的改善。张鸿等[3]研制了一种以燃料电池为主供电源的分布式能源系统，采用模糊PID 算法设计，避免燃料电池出现功率急变，延长了工作寿命。薛晓东等[4]对常用中小型发电装置的优缺点进行了对比分析，为分布式供能系统的发电装置选型以及系统方案设计提供了参考。牛天钰等[5]以某医院为例，确定了燃气冷热电联供能源系统的装机规模和系统配置，并从经济、能源利用效率及环境3方面分析了该能源系统的合理性。张伟波等[6]论述了多能互补综合供能系统的主要技术特征、系统构成与关键技术，并结合某创新园开发了“五化一体”供能实施方案，为分布式能源系统的开发提供了新的视角。Ou 等[7]研制的基于燃料电池的微热电联产系统已经应用于某住宅小区，通过仿真证明了通过对系统功率优化分配，能够实现系统高效安全运行，考虑水箱热条件的情况下，系统效率提高了20%。Tazay 等[8]为学校建筑的混合可再生能源系统提供了详细的可行性分析，探究了氢能组件、光伏组件对系统技术性和经济性的影响。Li 等[9]为了保证燃料电池系统在有轨电车上的稳定运用，提出了基于在线极值寻求的能量管理策略，与状态机控制策略和等效耗氢最小化策略相比，可节约耗氢43.92%和23.49%，提高堆效率2.61%和17.31%。Soberanis 等[10]确定了影响实施储能系统可行性的主要因素，提出了一种适用于不同存储功能和应用领域的通用方法。

然而目前的研究大多没有关于系统成本与效率的针对性分析，成本与效率之间的关系比较模糊，对系统的规模优化也有待探索。本文以一个典型的商场为研究目标，提出了一种以燃料电池为核心的能源供应系统，并分析了成本与总效率的平衡点，优化了能源系统配置。

1 系统概述

离网能源系统大多应用在独栋建筑上，或对一片特定区域进行供电，实现脱网孤岛运行，而大型商场一般为独栋楼宇结构，而且其作为娱乐购物场所，用电行为特点与周边居民楼、工业园区等有很多不同之处。本文以大型商场为研究对象，从理论角度上分析离网能源系统的适用性与经济性。

假设某大型商场商业建筑面积为25 000 m2，营业时间为10:00—22:00，商场用电主要可概括为三大部分：空调系统用电、照明用电、动力设备用电。空调一般在营业前1 h打开，随外界温度的变化在午后达到运行峰值，而照明和动力设备用电在营业时间内基本处于小范围波动的稳定状态。商场的用电行为可以概括如图1 所示。商场单日负载需求峰值为2 035 kW，为了保证商场电力系统的可靠运行，若仅以燃料电池作为供应电源，其最大功率需在负载需求峰值以上，这势必会导致成本的大幅增长，且会产生不必要的能源损失。但储能装置应用之后，两者同时供电可满足商场的负载需求，且可以将燃料电池的最大功率降到比较小的范围。在满足单日负载需求的同时，实现能源的合理配置。

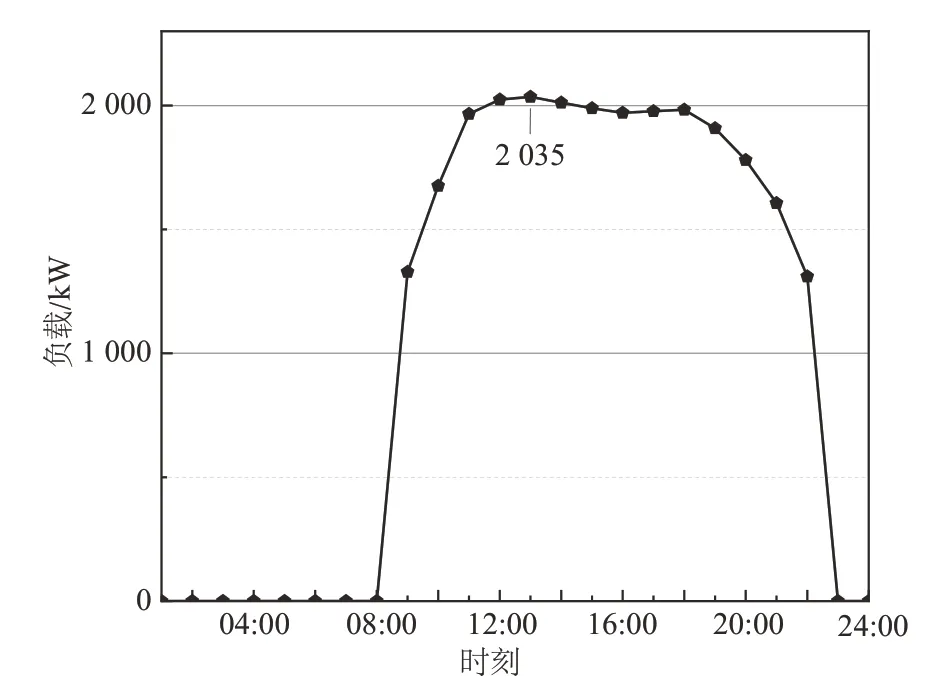
图1 购物中心负载逐时变化曲线Fig.1 Hourly average load demand curve during a day of shopping mall

燃料电池根据工作温度的不同可以分为低温、高温两大类，高温质子交换膜燃料电池(high temperature PEMFC，HT-PEMFC)因工作温度大于100 ℃而不需要考虑反应生成的水等一系列衍生问题，且温度升高使催化剂对CO 中毒的耐受性也有所提高，故本方案选取高温质子交换膜燃料电池作为供应电源。

根据储能技术充放电性能特征，有能量型和功率型2 种。能量型储能的能量密度较大，充放电时间较长，适合在能量需求较高的场合中使用，主要有液流电池、锂离子电池等；功率型储能的功率密度大，能够快速响应，适合在功率需求较高的场合使用，主要有超级电容、飞轮储能等。考虑大型商场的储能功用，优先选取能量型储能。锂元素的优良特性使锂电池具有很高的能量密度，但其制造与加工成本较高，且锂电池大规模使用的安全性问题仍待攻克。而液流电池的反应活性物质是作为电解质水溶液存储在外部独立的储液罐中，通过循环泵的带动在电池和管道中进行流动，然后在电极上发生离子价态的变化，从而实现能量的存储与释放，因此液流电池具有极高的安全性。而且液流电池的这一特性也导致了其容量和功率是相互独立的，可以通过增加电池电堆的大小来提高功率，通过提高电解液的浓度和体积来增大电池的容量，具有很高的设计灵活性。

其中尤以全钒液流电池(vanadium redox flow battery，VRFB)商业化程度最高，由于其采用同种元素(正极：VO2+/VO+2，负极：V2+/V3+)组成电解液系统，故从原理上杜绝了反应活性物质在正负半电池之间的交叉污染，其能量效率可达90%，充放电循环次数可超13 000 次，性能远高于现有二次电池。

基于大型商场对电力供应系统高安全性、高可靠性的实际要求，通过横向对比各类储能技术，选取全钒液流电池作为能源系统中的储能装置，系统框图如图2所示。

图2 混合能源系统图Fig.2 Hybrid energy system diagram

整个系统由高温质子交换膜燃料电池全钒液流电池(all-vanadium redox flow battery，VRFB)以及变换器(DC/DC、DC/AC)组成。

2 模型建立

2.1 高温质子交换膜燃料电池

高温质子交换膜燃料电池由双极板和膜电极组成，膜电极是燃料电池的核心部件，包括阴极电极、质子交换膜和阳极电极。电极上发生的反应如下所示：

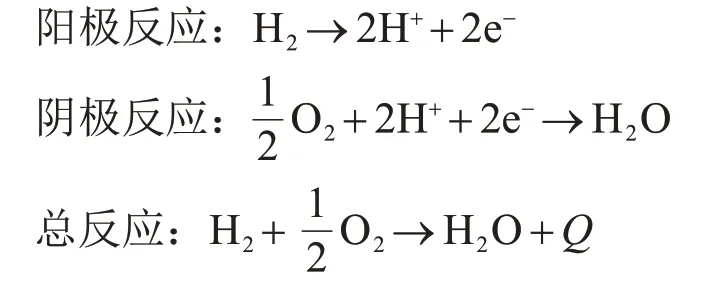
其中Q为反应热，kJ·mol-1。

由于燃料电池内部复杂的传热传质工况，一般情况下其输出电压会受到活化损失、欧姆损失和传质损失3方面的损失，故燃料电池的实际输出电压为

式中：ENernst为能斯特电压，V；Vact为活化损失，V；Vohm为欧姆损失，V；Vconc为传质损失，V。

能斯特方程只包含浓度对内部电势的影响，所以一般采用涵盖温度修正的能斯特方程来求解电池的内部电势：

式中：为标准状态下燃料电池的内部电势，V；ΔS0为标准状态下每摩尔氢气反应产生的总熵变，J·mol-1·K-1；T为反应温度，K；T0为标准状态下的温度，298.15 K；R为理想气体常数，取值为8.314 J·mol-1·K-1；F为法拉第常数，96 485 C/mol；PH2为氢气分压力；PO2为氧气分压力。

为了满足输出要求，燃料电池一般都是由单电池串联在一起使用的，其输出功率可由式(3)表示。燃料电池的效率也可以利用输出功率与氢气低热值和质量流率乘积的比值来表示，如式(4)所示。

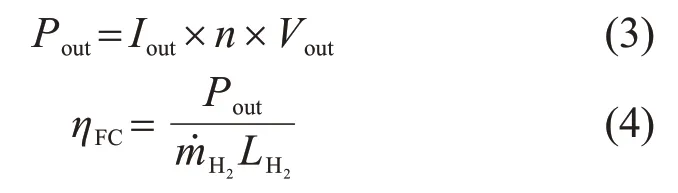
式中：Iout，Vout和Pout分别为燃料电池的输出电流、输出电压和功率；n为单电池的片数；ηFC为燃料电池效率；m˙H2为流量，mol/s；LH2为氢气的低热值，取值为241 kJ/mol。

认为反应过程使用空气(氧气体积分数为21%)作为电池阴极的输入时，高温质子交换膜燃料电池的电压-电流、功率-电流特性如图3所示。

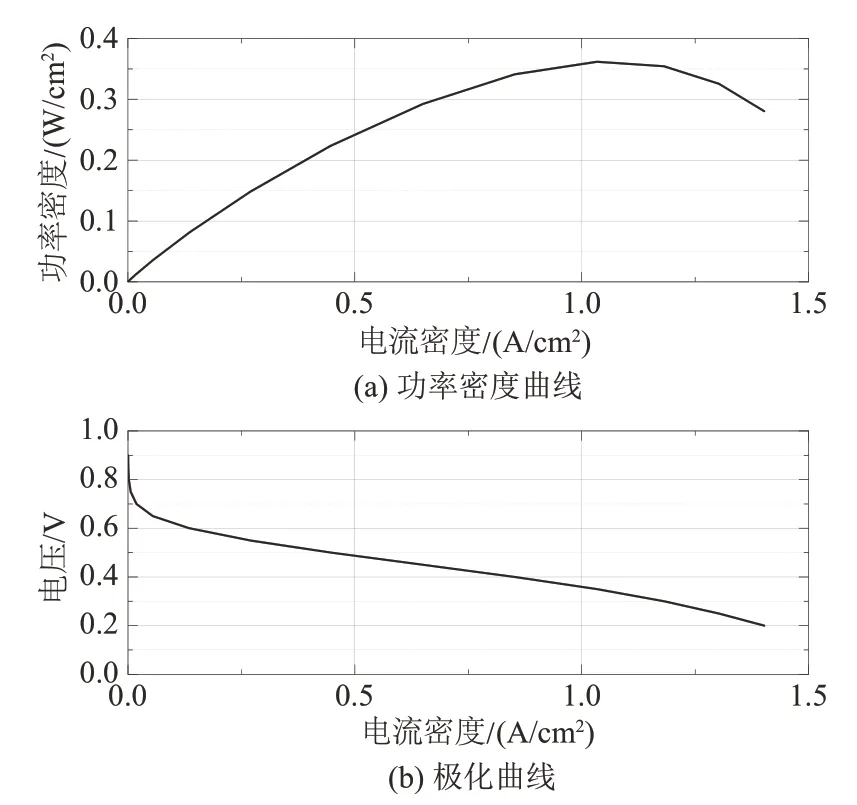
图3 HT-PEMFC特性曲线Fig.3 Characteristic curves of HT-PEMFC

结合实际运行工况，燃料电池是否全功率运行，其效率并非保持不变，负载率与运行效率整体呈非线性变化趋势，对应关系如图4 所示。燃料电池的效率可以理解为热力学效率、电压效率与电流效率的乘积，而电流效率一般为1，热力学效率是一个固定值，故在负载率变化的情况下燃料电池的效率与电压效率有类似的变化趋势，而电压效率取决于3 个电压损失，故燃料电池的效率与极化曲线有相似的变化趋势[11]。

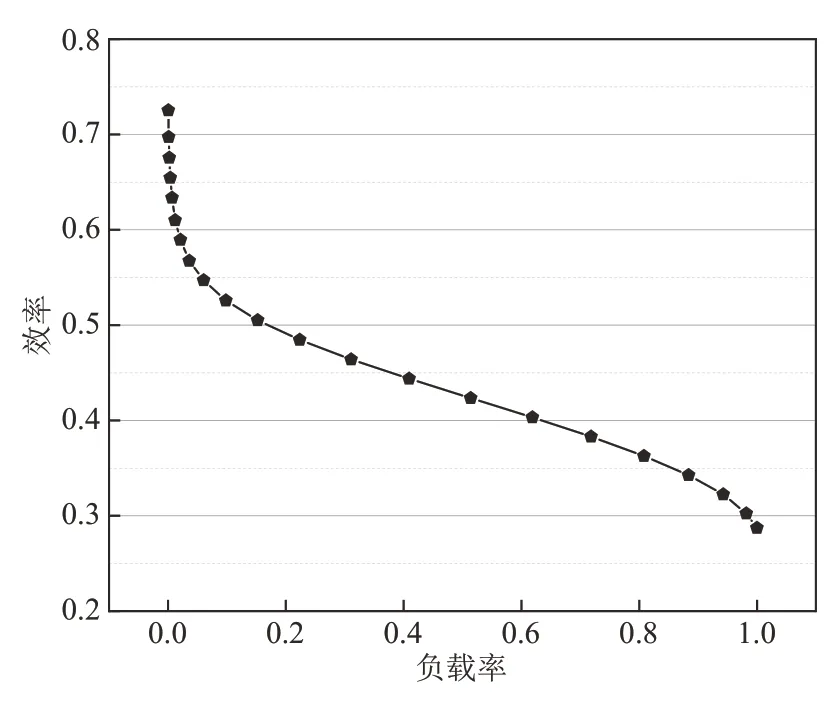
图4 负载率-效率曲线Fig.4 Load rate-efficiency curve

2.2 全钒液流电池

全钒液流电池包括电池本体、外部电解液储罐、泵以及电解液循环管路，电解液通过泵的作用在电池和储罐之间循环流动。并且发生以下电化学反应，实现电能与化学能的相互转化，进而完成能量的存储与释放过程。

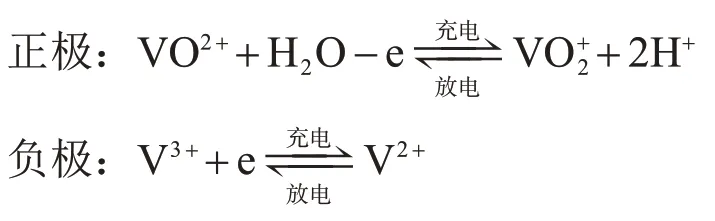
总反应：

一般地，全钒液流电池的单体电位可由能斯特方程表示：

式中E0为单体的开路电压值，一般为1.255 V。

全钒液流电池的充放电过程可由荷电状态(state of charge，SOC)来表示，全钒液流电池在任意时刻的电量都由电解液中反应活性物质(钒离子)的量决定，由式(6)可知SOC 与电解液中的钒离子相关联，故通过SOC可以反映系统任意时刻的电量百分比。

实际应用中，为了规避电池的过充过放现象，一般都确保全钒液流电池工作在(0.1～0.9)SOC，延长电池使用寿命。

目前关于全钒液流电池充放电方式的研究仍有待深入，常用的2 种方法是恒电流法和恒功率法。基于文献[12]的研究可知，2种充电方式对电池的能量效率并不产生决定性影响。但充电过程会因功率增大而对电池充电效率产生一定的影响，如功率从250 W增大到2 500 W，充电效率从95%降至89.5%。燃料电池对液流电池的充电属于恒功率充电，后面经济性分析时可以忽略功率变化对充电效率产生的影响，以减少分析变量。

3 系统评估和优化方法

3.1 基本参数

系统中的高温质子交换膜燃料电池、全钒液流电池及逆变器作为系统的主要组件，其相关基本参数(成本、寿命、效率)如表1 所示[13-15]，结合实际需求，假定该项目设计寿命为20 a。

表1 组件的关键参数Tab.1 Key parameters of components

系统的实际效率取决于质子交换膜燃料电池与液流电池之间的比例关系，考虑到系统需要逆变器的辅助，将直流电转化为交流电后才能直接向负载供电，故燃料电池直接供应负载的实际效率为0.95。若燃料电池产生的电量先储存至液流电池，随后由液流电池向负载供电，则效率降低至0.731(0.95×0.9×0.9×0.95)。

3.2 评估指标

混合能源系统的评价指标从2个角度考虑可以分为经济性指标和技术性指标，系统的经济性主要体现在初始成本和年化成本上，如式(7)—(11)所示：

式中：Ci为系统初始成本；Cz，x为组件x的资本成本；Sx为组件x的规模大小。

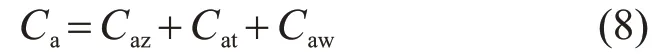
式中：Ca为系统总年化成本；Caz为系统年化资本成本；Cat为系统年化替换成本；Caw为系统年化运维成本。

式中：Caz，x为组件x的年化资本成本；Cz，x为组件x的资金成本；i为一次成本和年化成本转换的折现率，0.15；Ls为系统设计寿命，其值为20 a。

式中：Cat，x为组件x的年化更新成本；Ct，x为组件x的更新成本；Lx为组件使用寿命。

式中：Caw，x为组件x的年化运维成本；Cw，x为组件x的运维成本。

系统的效率可以比较直观地反映整体的性能，故选取系统效率、总效率作为评价系统技术性能的指标，被定义为

式中：ηsys为系统效率；ηtotal为系统运行总效率；EFC为燃料电池提供给负载的能量；EBAT为液流电池提供给负载的能量；ET为燃料电池产生的能量。

3.3 确定最优系统配置

由图1可知，该商场单日负载峰值为2 035 kW,单日用电量需求为25 565 kW·h。假设燃料电池工作24 h，若要满足用电量需求，则燃料电池功率最小值需为1 121.3 kW。分析燃料电池与液流电池的实际应用场景可知，22:00 至第2 天09:00，这个时段共计11 h，可由燃料电池向液流电池充电，以弥补白天燃料电池功率输出的不足。对燃料电池的功率临界点1 121.3 kW 进行分析，此时发电量为26 911.2 kW·h，结合图1 可知，燃料电池可直接向负载提供13 848 kW·h 的电量，其余的电量则需存储在液流电池中，由表1 可知，燃料电池的电量经过液流电池再供给负载的效率为0.731，故液流电池可向负载提供9 016.4 kW·h的电量，此时并不能满足商场的单日用电量需求，以此倒推可知当燃料电池的最大功率为1 253.7 kW 时，燃料电池与液流电池构成的混合能源系统可以满足该购物中心的用电需求。即燃料电池的运行功率最小值为1 253.7 kW，此时液流电池的容量为14 740 kW·h，其所需的充电时间一定能被满足，液流电池的功率和容量是相互独立的，通常来说容量一般是功率数值的20 倍左右，故在此方案中液流电池的成本以容量成本为准。

由图4可知，燃料电池的负载率越小，其效率越高，保持燃料电池的运行功率不变，不断累加电池堆的片数，使电池的最大功率不断提高，进而降低电池的负载率。虽然负载率降低使得效率提高，间接减少了系统上游的用氢成本，但燃料电池的硬件成本也不断增加。本文着重分析用氢成本和硬件成本这2个影响系统总成本的主要因素。保持燃料电池的运行功率不变，相当于间接固定了液流电池的容量，进而将这一多目标优化问题转化为控制燃料电池的负载率，寻找系统总年化成本最小的单目标优化问题。确定系统总成本最小值配置的流程如图5 所示。

图5 确定最小成本系统配置流程图Fig.5 Flowchart of ascertaining the minimal cost system configuration

4 系统分析

考虑到燃料电池运行效率的变化，将系统上游的用氢成本也纳入分析范围，保持运行功率不变，最大功率越高，电池负载率越低。由图4所示的变化规律，可得单日用氢成本与燃料电池最大功率的关系，如图6所示。从供货商处得知99.9%高纯氢的成本为0.536 1美元/L。

图6表明了电池堆负载率从100%降至0.16%与用氢成本的对应关系，A点对应燃料电池的最大功率为4 032.8 kW，工作负载率为31.08%，此时燃料电池的运行效率为46.424%。A点之前，负载率从100%降至31.08%，单日用氢成本实现了掉落式下降，系统增益明显。这是因为对应区间燃料电池最大功率的涨幅并不大，故这段区间上的曲线显得比较陡峭。其后随着负载率的下降，电池运行效率仍逐渐增加，且在负载率趋于0时效率增幅明显，用氢成本仍保持下降，但相对于电池功率的大幅增加，整体曲线变化趋缓，幅度并不大。

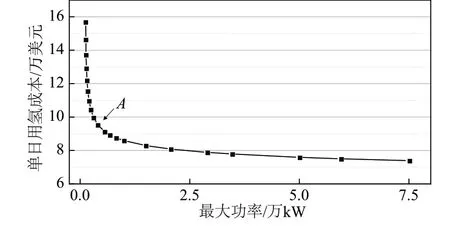
图6 最大功率与单日用氢成本关系Fig.6 Relationship between the rated power and daily hydrogen cost

该工程项目设计寿命为20 a，由表1可知，燃料电池的使用寿命为7 a，在项目周期内要经历2次更换，根据式(9)和式(10)将项目周期内燃料电池的硬件成本折为年化成本。图7为燃料电池最大功率与硬件年化成本之间的关系，可以发现，燃料电池的最大功率与成本呈线性正相关，随着燃料电池的最大功率增大，电池硬件成本也迅速上升。

图7 燃料电池最大功率与年化成本关系Fig.7 Relationship between the rated power and annualized cost

考虑到系统组件在项目周期内的更新、运维，以及资金的时间价值，利用公式(7)—(11)将系统各组件(燃料电池、液流电池、逆变器、转换器)硬件成本以及用氢成本等所有投资金额折为年金现值，再转化为年化成本，方便统一分析。得到了燃料电池电池堆规模大小与总年化成本之间的关系，如图8所示。此方案中液流电池的容量维持不变，即液流电池的成本不变，且转换器的成本也保持不变，故液流电池和转换器的成本并不对总年化成本的变化趋势产生影响，随着燃料电池堆栈片数的增加，即最大功率的提高，电池负载率呈下降趋势，而燃料电池的效率逐渐上升，导致年用氢成本不断下降，但燃料电池的硬件成本不断攀升。可以发现在B点之前，对应图6的前端，单日用氢成本实现了掉落式下降，转换为年用氢成本亦如此，而此阶段燃料电池最大功率提升的倍数不大，硬件成本升高的幅度远不足以与年用氢成本相抵消，故此阶段总年化成本与年用氢成本的变化趋势一致。B点对应的燃料电池最大功率为5 604.75 kW，负载率为22.368%，燃料电池运行效率为48.462%，此时系统总年化成本取得最小值38 302 837.5美元。B点之后，虽然燃料电池负载率仍在降低，但此阶段用氢成本的减小幅度已经不足以弥补电池堆规模大幅增长引起的硬件成本的增长，故系统总年化成本基本随燃料电池最大功率的增加而快速增长。

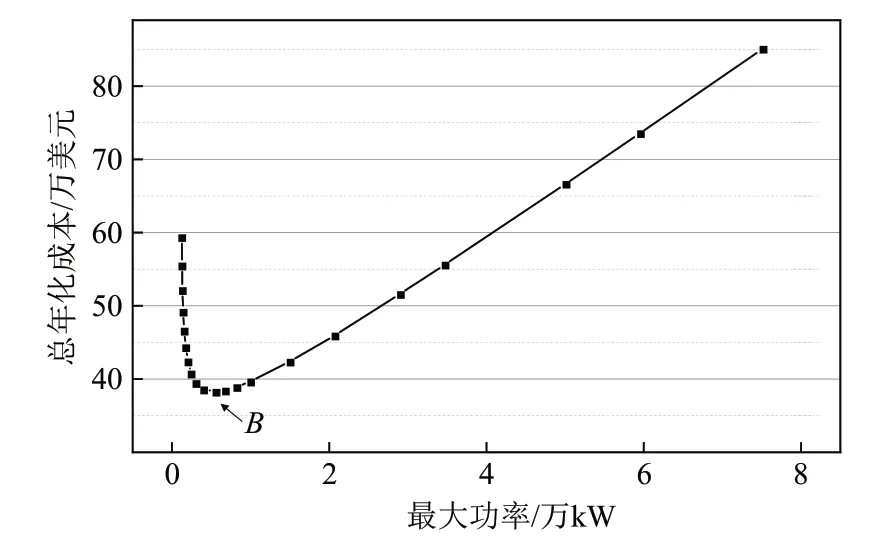
图8 燃料电池最大功率与总年化成本关系Fig.8 Relationship between the rated power and total annualized cost

5 结论

离网能源系统主要应用在独栋建筑或一定区域内进行脱网孤岛运行，以大型商场为研究对象，从理论角度分析此场景下所提出的能源系统的可行性与经济性，得出以下结论：

1）利用所提出的评估指标，确定总年化成本最小时的系统配置，可以发现系统总年化成本在燃料电池负载率为22.368%时取得最小值，相对于百分百负载的情况，系统投资成本上升了212.5%，燃料成本下降了41.7%，系统总年化成本下降了35.5%，整体增益明显。

2）关于燃料电池与液流电池构成的混合能源系统的效益，探讨的方案对于以燃料电池为主供应电源的混合能源系统的配置优化有比较好的成效。对混合能源系统配置评估提供了一种可行的新思路，同时对混合能源系统在类似大型商超等独栋楼宇中的工程应用有一定的参考价值。

3）在确定最优系统配置方法上仍有不足，进一步的研究可以与智能算法相结合，完善系统配置选取的动态性与精确性。