半潜式海上风力机流固耦合特性分析
胡丹梅,曾理,陈云浩
(上海电力大学能源与机械工程学院,上海市 杨浦区 200090)
0 引言
随着化石能源的日益消耗,人类对新能源的研究日益加深。风能作为一种清洁无污染的可再生能源,受到人们的广泛关注[1]。随着技术的进步,海上风电以其土地资源零占用、风速更高且更稳定、流场中湍流强度小、视觉及噪声污染对环境影响小等优势,近年来得到了许多国家的重视[2]。与陆上风电相比,海上风力发电面临的发电环境更加复杂[3-5],不仅会受到盐雾对机组的腐蚀,还会受到波浪、浮冰、海流等对风力发电机组的冲击[6]。
海上风力发电机按基础划分一般分为固定式基础和漂浮式基础。浮式基础一般分为张力腿式(tension leg platform,TLP)、Spar 式、半潜式[7],其适用范围大多为水深超过50 m的海域。张力腿式对系泊缆材料要求较高。Spar 式基础水平面外运动响应较大,较TLP 式更适应深水。半潜式基础吃水小,在运输和安装时具有良好的稳定性,因此更具有经济性[8]。
国内外很多专家学者对海上半潜式风力机进行了研究。Masciola[9]等人研究了系泊系统对半潜式海上风力机模型运动响应的影响,主要分析了3 种不同波浪环境条件对整个风力机模型运动的影响,研究发现系泊线动力学在影响浪涌和升沉半潜式运动中的作用有限。Cheng[10]等人建立了海上浮式风力机的水动力模型,分析了风力机的气动性能,研究了气动力对浮式平台水动力响应的影响。刘海锋等[11]基于流固耦合理论,采用双向流固耦合方法和滑移网格技术对5 MW 风力机的尾迹特性进行了系统分析。邓新丽等[12]利用Blade 软件分析并计算了1.5 MW 风力机叶片在三维湍流下的载荷,发现叶片沿翼展方向应力最大且极限工况下的最大应力出现在离叶根1/3 的位置。Chen[13]等人基于2 种不同概念的半潜式海上风力机动力特性对比,从六自由度运动、气动阻尼效应、陀螺效应、塔顶动力响应以及系泊系统的动力学入手分析其性能。
以上研究大多对半潜式风力机模型运动进行动力响应分析,不能全面地观测风力机整机运行时的真实流场情况。本文除了对风力机进行整体的双向流固耦合分析,还利用仿真软件模拟实际运行时的环境载荷,在仿真软件中展现风及海水流过风力机的实际情况,以此对比整机的形变,流线图、形变云图等的变化,研究结果可为海上半潜式风力机设计提供参考。
1 半潜式风力机模型及计算域模型
1.1 半潜式风力机模型
根据叶素理论将美国国家可再生能源实验室(NREL)提供的参数进行坐标变换,进而将变换后的叶片坐标结果导入ProE构建叶轮模型。浮式平台的选取来源于Marco Masciola[5]所提供的平台数据,进而根据给定的东海水文数据对该半潜式浮式风力机进行建模。其中有关风力机整体构造数据及运行工况数据的详细参数如表1所示。
根据提供的模型数据对半潜式漂浮式风力机进行整体建模,整机模型如图1所示。

图1 半潜式浮式风力机结构模型Fig.1 Semi-submersible floating wind turbine structure model
1.2 计算域模型
设置轮毂中心为坐标原点,风力机逆风方向为Y轴正向,轴心至塔筒方向为Z轴正向,风力机风轮绕Y轴旋转,X轴方向由Y轴和Z轴右手法则决定。空气场上部半圆半径为150 m,气场高度为242 m;具体计算域尺寸设置为:空气场中的旋转域以风轮轮毂中心为原点,半径为70 m,厚度为5 m;下部分海水域高度设计为70 m;流体域入口距风力机150 m,风力机距流体域出口300 m。计算域整体模型如图2所示。

图2 计算域整体模型Fig.2 Overall model of computational domain
2 流固耦合理论
流固耦合作用是自然界客观存在的一种特殊现象,是指流体与固体之间的相互作用。流固耦合问题可由其耦合方程定义,这组方程的定义域同时有流体域与固体域。而未知变量含有描述流体现象的变量和含有描述固体现象的变量,一般具有以下特征[14]:
1)流体域与固体域均不可单独求解;
2)无法显式地削去描述流体运动的独立变量及描述固体现象的独立变量。
在流固耦合过程中,为保证流体与固体间能量的守恒,则在流体与固体的交界面处二者应满足以下方程:

式中:τ为应力;n为方向余弦;d为位移量;q为热流量;T为温度;下标f表示流体,s表示固体。
同时,可以建立控制方程的通式,对耦合简化分析需要结合模型所处的初始条件参数及相关边界条件。此时将流、固方程耦合到一个方程矩阵中进行求解,即在一个求解器中同时对流体和固体方程进行求解。方程如下:

式中:k为迭代时间步;Aff为流场的系统矩阵;Ass为固体的系数矩阵;ΔXfk为流体待求解力;ΔX ks为固体待求解力;Bf为流体外部作用力;Bs为固体外部作用力;Afs和Asf是流固耦合矩阵。
ANSYS 中采用的CFX 模块和瞬态模块中流体域计算与固体域计算之间流固耦合流程如图3所示。

图3 流固耦合流程图Fig.3 Fluid-structure coupling flow chart
3 网格划分及网格无关性验证
3.1 计算域网格划分及相关设置
由于需要确保双向耦合作用下流场域与固体域的数据传递准确性,划分时需要将叶片网格与旋转网格接触面的网格节点保持一致[15]。同时,由于风力机叶轮部分进行旋转,需要对此区域网格进行加密,使旋转时网格可以平稳过渡,确保数据传递的准确性。固体域网格如图4所示,并在Transient structural 中设置整个风力机表面为流固耦合面,3 条系泊缆绳底面设为固定面。

图4 风力机固体域网格Fig.4 Wind turbine structural domain grid
在风力机外部设置流体域,分别为风轮外部的旋转域,包含塔筒、风轮及一半浮筒的空气域,最后是下方的海水域。旋转域以风轮轮毂中心为原点,半径为70 m,厚度为5 m。空气域上部半圆半径为150 m,高度为300 m,下部海水域采用设计水深70 m。从流体域入口至风力机处为200 m,风力机距流体域出口为400 m,总长度为10R(R=63 m,为风轮半径)。整个流场域建好后划分网格,外部流场域采用六面体网格,内部旋转域采用四面体,如图5所示。

图5 流体域网格Fig.5 Fluid domain grid
3.2 数值计算方法与边界条件
本文基于Navier-Stocks 方程和RNGk-ε湍流模型[16],利用滑移网格及网格重构对NREL 5 MW半潜式风力机进行数值模拟,采用二阶迎风格式[17]。
控制方程为
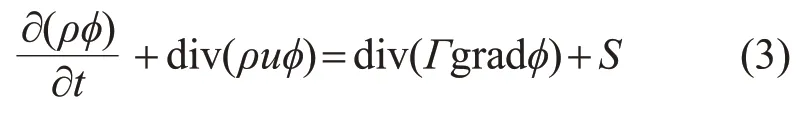
式中:ρ为流体密度;φ为通用变量;t为时间;u为来流风速;Γ为广义扩散系数;S为广义源项。
RNGk-ε湍流模型为:


式中:k和ε分别为湍动能及其耗散率;ui为流体速度分量;xi,xj为流体坐标分量;μeff为风流黏度与湍流黏度之和;Gk为平均速度梯度产生的湍动能;Gb浮力所产生的湍动能;YM为可压缩湍流中波动膨胀对总耗散率的贡献;αk和αε分别为湍动能及耗散率普朗特数的倒数;C1ε,C2ε和C3ε为模 型默 认常 数;Sk,Sε和Rε分 别为 用 户 定 义 的源项[18]。
CFX 定义的初始边界条件:入口为速度进口,风速为11.4 m/s,水流速度为0.5 m/s;出口为自由出流;外围流场区域设置为静止域wall,内部旋转域设置为interface;空气域与海水域交界处设为interface面,整个风力机设为wall。设置旋转域旋转角速度为1.267 rad/s,风轮跟随旋转域一起转动,设置网格重构。
3.3 功率验证
为了验证结果的准确性,采用不同网格数在机组的额定工况下进行数值计算。设置外流场入口为速度入口,出口为自由出流。额定风速为11.4 m/s,对应风轮转速为12.1 r/min,风轮表面以及外流场边界为无滑移壁面。
模拟采用SSTk-ω湍流模型,内外流场接触面设为interface,采用二阶迎风格式,收敛残差设置为1×10-4。分别设置风速为5、8、11.4 m/s,求对应的计算输出功率。
通过数值分析可以得到风轮转矩M,由式(6)可计算得到风力机的功率。
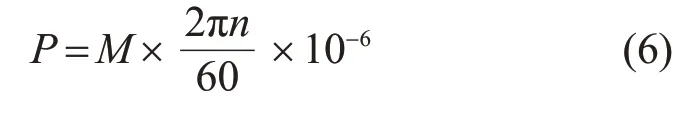
式中:P为风力机输出功率,MW;n为风力机额定工况下转速12.1 r/min。
图6 表明随着输入风速的增大,计算所得输出功率越来越接近于设计功率5 MW。当风速设置为额定风速11.4 m/s 时,计算得到输出功率为4.75 MW,相对于设计功率5 MW,误差仅为5%,在可接受的误差范围内。

图6 输出功率验证Fig.6 Computational domain model
4 风浪联合作用下风力机耦合分析
4.1 双向流固耦合计算域相关设置
利用Workbench平台构建双向流固耦合分析,在Mechnical 中构建结构域,在CFX 中构建流场域,在DM 中建立整个模型,并设置好相关边界条件。空气域与海水域交界面为interface 面,分别设置风速和水速,将整个半潜式风力机设置为耦合面。上部为空气域,下部为海水域。设置固体域与流体域运行时间均为10 s,即总时间为20 s,时间步长设置为0.1 s。同时,设置动网格开启,将各区域相连,实现数据传递。在计算中选择二阶欧拉方程,湍流选择二阶迎风格式,收敛残差设置为1.0×10-4。图7为计算域模型图。

图7 计算域模型图Fig.7 Computational domain model
在流体域中划分好流场网格,在结构域中划分好整机网格,导入流体域并进行双向流固耦合计算。在结构域中,风轮沿用NREL 5 MW 风力机中叶片设计的原材料,将玻璃纤维环氧树脂设定为叶片的复合材料,该材料具有成型后尺寸稳定、抗腐蚀以及承受载荷较大等优点,浮式平台的系泊缆选用聚酯纤维缆新型材料[19-20]。在流体域中分别设置空气域、海水域的入口、出口及壁面,空气域中的旋转域需设为interface 面,再将计算结果以压力载荷的方式导入结构,对风力机进行稳定性分析。
4.2 结构域应力应变分析
由文献[21]所知,风力机的转速与当时风速相关,本文所用NREL 5 MW 风力机转速与风速的关系如表2所示。

表2 不同风速下风力机转速Tab.2 Wind turbine speed at different wind speeds
根据表2,分别取5、8、11.4 m/s 风速下对应的风轮角速度以及风轮停止转动时的角速度0 rad/s,设置系泊缆底部为固定约束面,同时设置半潜式浮式风力机表面为流固耦合面,输出结构域中叶片的最大变形量。
图8为不同风力机转速下,叶片的最大变形量随时间的变化规律图。从图8中看出,当风轮转速为0 rad/s 时,风力机风轮停止转动,处于自存状态,叶片变形量随时间变化几乎不变,图上显示为一条直线,因此在自存状态下,风轮变形量可忽略不计。在1.267 rad/s 转速下,最大变形量峰值为21.038 mm;在0.959 rad/s 转速下,最大变形量峰值为11.866 mm;在0.773 rad/s转速下,最大变形量峰值则为7.757 mm。可见,随着风轮转速的增大,风轮的最大变形量也随之增大,且其峰值随转速的增大出现左移,即风轮转速越大,越早出现最大变形量。最大变形量在运行开始阶段变化较大,随着时间逐渐变小,在一定数值内趋于平缓。叶片变形主要受风力机转速(即输入风速)、材料影响,风轮转速增大(即输入风速增大),变形量明显提高。这一结论与张建平[20]所得结果一致,反映了叶片响应规律。在不同转速下,最大变形量随时间变化曲线的整体走势基本一致。

图8 不同转速下叶片最大变形量对比Fig.8 Comparison of maximum blade deformation at different speeds
从图8 可看出,在风轮停止运转时最大变形量随时间变化曲线几乎为直线,因此在等效应力曲线图中只讨论3种风轮转速,如图9所示。由图9可知,在风轮旋转初期,最大应力的变化很大,随着时间的推移,风轮最大等效应力逐步趋向平稳,并稳定在一定数值内变化,此时可判断风轮旋转,趋于稳定。且随着输入风速的增大,风轮转速随之增大,最大等效应力也随之增大。当风力机风轮转速设置为0.727 rad/s时,风轮的最大等效应力为8.01 MPa;风轮转速为0.959 rad/s时,其最大等效应力为12.44 MPa;风轮转速为1.267 rad/s时,其最大等效应力为21.46 MPa。由此可见,风轮等效应力值明显小于设计的材料许用应力值250 MPa。
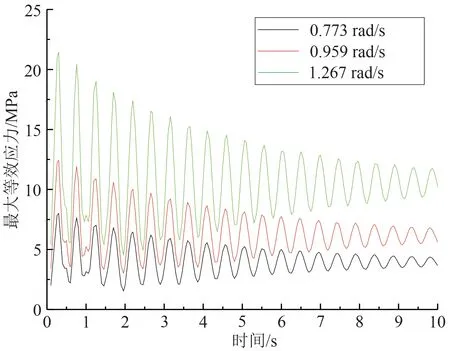
图9 风轮最大等效应力随时间变化图Fig.9 Maximum equivalent stress of the wind wheel changes with time
在流固耦合设置中将风速都设置为额定风速11.4 m/s。在额定风速下,将海水速度分别设置为0.5 m/s与2 m/s,对半潜式风力机浮式平台进行双向流固耦合特性分析。将双向流固耦合结果导出,在CFD-POST 中以云图的方式展示结果,如图10所示。
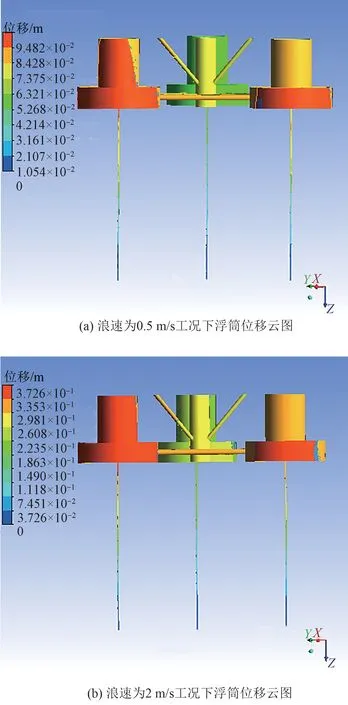
图10 风力机浮筒位移图Fig.10 Displacement cloud diagram of wind turbine foundation
浪速为0.5 m/s 时,浮筒最大位移为0.09 m。浪速为2 m/s时,浮筒最大位移为0.37 m。随着浪速的提升,浮筒位移显著增大,且位移最大处基本出现在下浮筒与系泊缆连接处附近。在浮筒部分,位移主要体现在系泊缆连接处,且系泊缆由于与浮筒相连,随浮筒一起运动。
为了更好地观察浮筒的运动情况,在CFX中导出浮筒及系泊缆位移参数,画出浮筒及系泊缆位移随时间变化曲线,如图11所示。

图11 浮筒及系泊缆位移随时间变化曲线图Fig.11 Float foundation and mooring line displacement curve diagram with time
由图11可以看出,在5.5 s左右位移达到最大值。可以合理地推测当时间进行到11 s 时,浮筒回到初始位置,完成一个周期运动。从原因分析,由于平台与系泊缆相连,平台受风浪联合作用,同时受到系泊缆拉力的作用,在变形过大时及时将平台拉回初始位置。
4.3 流体域速度流线分析
在额定风速11.4 m/s,海浪速度2 m/s工况下,在CFD-POST 中导出半潜式风力机流场域速度矢量图,如图12、13所示。

图12 风力机风轮附近速度矢量图Fig.12 Velocity vector diagram around wind turbine wheel

图13 流体域速度矢量图Fig.13 Velocity vector diagram of fluid domain
由图12 可知,风轮处速度由叶尖向叶根递减,在半潜式风力机中速度最大存在于叶尖部分,且叶尖处速度矢量密度最大,速度约为87.5 m/s。在风轮部分可以清晰地观察到风轮旋转时的速度矢量。在半潜式平台部分,发现围绕系泊缆区域,速度矢量明显高于海水域其他部分,易形成绕流。图14为在额定风速11.4 m/s、海浪速度2 m/s 工况下风力机的流线图,其中用粗实线标出的为风力机叶轮所在位置。从图14中可以看出,风流经风力机后发生偏转,流线有一定紊乱,但经过旋转域后逐渐恢复稳定。

图14 风力机流线图Fig.14 Wind turbine streamline diagram
5 结论
对半潜式风力机进行双向流固耦合特性分析,结论如下:
1)在不同风速对应的风轮转速下,随转速的增大,风轮形变增大,且峰值出现左移,即转速越大,越早出现最大变形量。最大变形量的大小随着时间的变化,逐渐趋于平缓,并最终稳定。叶片变形主要受风力机转速(即输入风速)、材料影响,其中受风速影响较大。在运行开始后0.3 s,风轮变形量达到最大值。
2)随着时间推移,风力机半潜式平台位移与等效应力值都趋于稳定。风力机等效应力值在所设工况中符合设计要求,明显小于设计的材料应力值250 MPa。且在结构分析中未出现较大程度变形,符合设计结构稳定性要求。
3)在风力机运行过程中,叶片的变形集中于叶尖附近,且越靠近叶尖越明显。在整机中,形变主要集中于系泊缆连接处。因此,叶片及浮筒系泊缆的材料选取尤为重要。经测算,浮筒与系泊缆的振动周期约为11 s。因此在系泊缆处应进行加固或选用更结实的材料。
4)根据半潜式风轮速度矢量图,可看出叶尖至叶片中段速度较大,颜色较深。风力机流线图显示风经过风轮产生一定扰动,后逐渐稳定,流场流线基本稳定。

